Купол (геометрия)

Набор куполов
Набор куполов
	Пятиугольный пример
Лица	n треугольников , ; n квадратов , ; 1 н -гон , ; 1 2 н -гон
Края	5 н
Вершины	3 н
Символ Шлефли	{ п } \|\| т { н }
Группа симметрии	C n v , [1, n ], (* nn ), порядка 2 n
Группа ротации	С н , [1, н ] + , ( nn ), порядок n
Двойной многогранник	?
Характеристики	выпуклый , призматоидный

В геометрии купол твердое представляет собой тело, образованное путем соединения двух многоугольников , один (основание) с вдвое большим количеством ребер , чем другой, чередующейся полосой равнобедренных треугольников и прямоугольников . Если треугольники равносторонние , а прямоугольники — квадраты , а основание и противоположная ему грань — правильные многоугольники , то треугольные , квадратные и пятиугольные купола относятся к телам Джонсона и могут быть образованы, взяв сечения кубооктаэдра , ромбокубооктаэдра , и ромбокододекаэдр соответственно.

Купол можно рассматривать как призму , в которой один из многоугольников сложен пополам путем слияния альтернативных вершин.

Куполу можно присвоить расширенный символ Шлефли ${n} || t{n},$ представляющий правильный многоугольник ${n},$ параллелью его усечения соединенный $t {n}$ или ${2 n}.$

Купола — подкласс призматоидов .

Его двойник содержит форму, которая является своего рода сварным швом между половиной $n$ -стороннего трапецоэдра и $2 n$ -сторонней пирамидой .

Примеры

Семейство выпуклых куполов
v
т
и
н	2	3	4	5	6	7	8
Символ Шлефли	${2} \|\| т{2}$	${3} \|\| т{3}$	${4} \|\| т{4}$	${5} \|\| т{5}$	${6} \|\| т{6}$	${7} \|\| т{7}$	${8} \|\| т{8}$
Купол	Диагональный купол	Треугольный купол	Квадратный купол	Пятиугольный купол	Шестиугольный купол (Плоский)	Семиугольный купол (Необычное лицо)	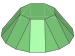Восьмиугольный купол (Необычное лицо)
Связанный униформа многогранники	Ромбоэдр	Кубооктаэдр	Ромбокубооктаэдр	Ромбикосидодекаэдр	Ромбитригексагональная плитка	Ромбитригептагональная черепица	Ромбитриоктагональная черепица

Упомянутые выше три многогранника — единственные нетривиальные выпуклые купола с правильными гранями: « Шестиугольный купол» — плоская фигура, а треугольную призму можно считать «куполом» 2-й степени (купол отрезка и квадрат). Однако купола многоугольников более высокой степени могут быть построены с неправильными треугольными и прямоугольными гранями.

Координаты вершин

Определение купола не требует, чтобы основание (или сторона, противоположная основанию, которую можно назвать вершиной) была правильным многоугольником, но удобно рассмотреть случай, когда купол имеет максимальную симметрию $C n v$ . В этом случае вершиной является правильный $n$ -угольник, а основанием является либо правильный $2n -$ угольник, либо $2n -$ угольник, у которого две разные длины сторон чередуются и те же углы, что и у правильного $2n -$ угольника. Удобно зафиксировать систему координат так, чтобы основание лежало в $плоскости xy$ , а вершина - в плоскости, параллельной $плоскости xy$ . Ось $z$ является $осью n-$ кратности, а плоскости зеркала проходят через $ось z$ и делят стороны основания пополам. Они также делят пополам стороны или углы верхнего многоугольника, или и то, и другое. (Если $n$ четное, половина зеркальных плоскостей делит пополам стороны верхнего многоугольника и половина — углы, а если $n$ нечетное, каждая зеркальная плоскость делит пополам одну сторону и один угол верхнего многоугольника.) Вершины основания можно обозначить ⁠ $V_{1}$ ⁠ через ⁠ $V_{2n},$ ⁠ а вершины верхнего многоугольника можно обозначить ⁠ $V_{2n+1}$ ⁠ через ⁠ $V_{3n}.$ ⁠ С учетом этих соглашений координаты вершин можно записать как: ${\begin{array}{rllcc}V_{2j-1}:&{\biggl (}r_{b}\cos \left({\frac {2\pi (j-1)}{n}}+\alpha \right),&r_{b}\sin \left({\frac {2\pi (j-1)}{n}}+\alpha \right),&0{\biggr )}\\[2pt]V_{2j}:&{\biggl (}r_{b}\cos \left({\frac {2\pi j}{n}}-\alpha \right),&r_{b}\sin \left({\frac {2\pi j}{n}}-\alpha \right),&0{\biggr )}\\[2pt]V_{2n+j}:&{\biggl (}r_{t}\cos {\frac {\pi j}{n}},&r_{t}\sin {\frac {\pi j}{n}},&h{\biggr )}\end{array}}$

для $j = 1, 2, ..., n$ .

Поскольку многоугольники ⁠ $V_{1}V_{2}V_{2n+2}V_{2n+1},$ ⁠ и т. д. являются прямоугольниками, это накладывает ограничение на значения ⁠ $r_{b},r_{t},\alpha .$ ⁠ Расстояние ${\bigl |}V_{1}V_{2}{\bigr |}$ равно ${\begin{aligned}&r_{b}{\sqrt {\left[\cos \left({\tfrac {2\pi }{n}}-\alpha \right)-\cos \alpha \right]^{2}+\left[\sin \left({\tfrac {2\pi }{n}}-\alpha \right)-\sin \alpha \right]^{2}}}\\[5pt]=\ &r_{b}{\sqrt {\left[\cos ^{2}\left({\tfrac {2\pi }{n}}-\alpha \right)-2\cos \left({\tfrac {2pi}{n}}-\alpha \right)\cos \alpha +\cos ^{2}\alpha \right]+\left[\sin ^{2}\left({\tfrac {2\pi }{n}}-\alpha \right)-2\sin \left({\tfrac {2\pi }{n}}-\alpha \right)\sin \alpha +\sin ^{2}\alpha \right]}}\\[5pt]=\ &r_{b}{\sqrt {2\left[1-\cos \left({\tfrac {2\pi }{n}}-\alpha \right)\cos \alpha -\sin \left({\tfrac {2\pi }{n}}-\alpha \right)\sin \alpha \right]}}\\[5pt]=\ &r_{b}{\sqrt {2\left[1-\cos \left({\tfrac {2\pi }{n}}-2\alpha \right)\right]}}\end{aligned}}$

в то время как расстояние ${\bigl |}V_{2n+1}V_{2n+2}{\bigr |}$ равно ${\begin{aligned}&r_{t}{\sqrt {\left[\cos {\tfrac {\pi }{n}}-1\right]^{2}+\sin ^{2}{\tfrac {\pi }{n}}}}\\[5pt]=\ &r_{t}{\sqrt {\left[\cos ^{2}{\tfrac {\pi }{n}}-2\cos {\tfrac {\pi }{n}}+1\right]+\sin ^{2}{\tfrac {\pi }{n}}}}\\[5pt]=\ &r_{t}{\sqrt {2\left[1-\cos {\tfrac {\pi }{n}}\right]}}\end{aligned}}$

Они должны быть равны, и если это общее ребро обозначено $s$ , ${\begin{aligned}r_{b}&={\frac {s}{\sqrt {2\left[1-\cos \left({\tfrac {2\pi }{n}}-2\alpha \right)\right]}}}\\[4pt]r_{t}&={\frac {s}{\sqrt {2\left[1-\cos {\tfrac {\pi }{n}}\right]}}}\end{aligned}}$

Эти значения необходимо подставить в приведенные ранее выражения для координат вершин.

Звезды-купола

Семейство звезд-куполов
v
т
и
4	5	7	8	$.mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}n ⁄ d$
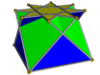{4/3} Перекрещенный квадратный купол (с ног на голову)	{5/3} Перекрещенный пентаграммный купол (с ног на голову)	{7/3} Гептаграммный купол	{8/3} Октаграммный купол	3
—	—	{7/5} Скрещенный гептаграммный купол (с ног на голову)	{8/5} Скрещенный октаграммный купол	5

Семья звездчатых куплоидов
v
т
и
3	5	7	$n ⁄ d$
{3/2} Перекрещенный треугольный куплоид (с ног на голову)	{5/2} Пентаграммный куплоид	{7/2} Гептаграммный куплоид	2
—	{5/4} Перекрещенный пятиугольный куплоид (с ног на голову)	{7/4} Перекрещенный гептаграммный куплоид	4

Звездные купола существуют для любого верхнего основания ${n / d},$ где $6/5 < n / d < 6$ и $d$ нечетно. В этих пределах купола разрушаются в плоские фигуры. За этими пределами треугольники и квадраты больше не могут охватывать расстояние между двумя базовыми многоугольниками (его все еще можно создавать с помощью неравносторонних равнобедренных треугольников и неквадратных прямоугольников). Если $d$ четно, нижняя база ${2 n / d}$ становится вырожденной; тогда мы можем сформировать купол или полукупол, убрав эту вырожденную грань и позволив треугольникам и квадратам соединяться здесь друг с другом (через одиночные ребра), а не с нижним основанием (через его двойные ребра). В частности, тетрагемигексаэдр можно рассматривать как ${3/2}$ -куполоид.

Все купола ориентируемые , а куполоиды неориентируемые. Для куполоида, если $n / d > 2$ , то треугольники и квадраты не покрывают все (единственное) основание, и в этом основании помещается небольшая мембрана ${n / d}$ -угольника, которая просто перекрывает пустое пространство. Следовательно, ${5/2}$ - и ${7/2}$ -куполоиды, изображенные выше, имеют мембраны (не заполнены), тогда как ${5/4}$ - и ${7/4}$ -куполоиды, изображенные выше, не имеют.

Высота $h$ -купола ${n / d}$ или купола определяется по формуле: $h={\sqrt {1-{\frac {1}{4\sin ^{2}\left({\frac {\pi d}{n}}\right)}}}}.$ В частности, $h = 0$ в пределах $n / d = 6$ и $n / d = 6/5$ , а $h$ максимизируется при $n / d = 2$ (в двуугольном куполе : треугольная призма, где треугольники стоят вертикально). ^[1]^[2]

На изображениях выше звездным куполам присвоена последовательная цветовая схема, чтобы облегчить идентификацию их лиц: основание ${n / d}$ -угольника красное, основание ${2 n / d}$ -угольника желтое, квадраты синие. , а треугольники зеленые. У куполоидов основание ${n / d}$ -угольника красное, квадраты жёлтые, а треугольники синие, так как основание ${2 n / d}$ -угольника убрано.

Гиперкуполы

Гиперкуполы представляют или многогранные купола собой семейство выпуклых неоднородных полихор (здесь четырехмерных фигур), аналогичных куполам. Основаниями каждого из них являются Платоново тело и его расширение . ^[3]

Имя	Четырехгранный купол		Кубический купол		Октаэдрический купол		Додекаэдрический купол		Шестиугольный черепичный купол
Символ Шлефли	${3,3} \|\| рр{3,3}$		${4,3} \|\| рр{4,3}$		${3,4} \|\| рр{3,4}$		${5,3} \|\| рр{5,3}$		${6,3} \|\| рр{6,3}$
Сегментохора индекс ^[3]	К4.23		К4.71		К4.107		К4.152
радиус	$1$		${\textstyle {\sqrt {\frac {3+{\sqrt {2}}}{2}}}\approx 1.485634}$		${\textstyle {\sqrt {2+{\sqrt {2}}}}\approx 1.847759}$		${\textstyle 3+{\sqrt {5}}\approx 5.236068}$
Изображение
Крышечные клетки
Вершины	16		32		30		80		∞
Края	42		84		84		210		∞
Лица	42	24 треугольника 18 квадратов	80	32 треугольника 48 квадратов	82	40 треугольников 42 квадрата	194	80 треугольников 90 квадратов 24 пятиугольника	∞
Клетки	16	1 тетраэдр 4 треугольные призмы 6 треугольных призм 4 треугольные пирамиды 1 кубооктаэдр	28	1 кубик 6 квадратных призм 12 треугольных призм 8 треугольных пирамид 1 ромбокубооктаэдр	28	1 октаэдр 8 треугольных призм 12 треугольных призм 6 квадратных пирамид 1 ромбокубооктаэдр	64	1 додекаэдр 12 пятиугольных призм 30 треугольных призм 20 треугольных пирамид 1 ромбокосододекаэдр	∞	1 шестиугольная плитка ∞ шестиугольные призмы ∞ треугольные призмы ∞ треугольные пирамиды 1 ромбитригексагональная плитка
Связанный униформа полихора	сморщенный 5-клеточный		сморщенный тессеракт		сморщенный 24-клеточный		сморщенный 120-клеточный		срезанные шестиугольные соты для плитки

См. также

Ссылки

^ «куполы» . www.orchidpalms.com . Проверено 21 апреля 2018 г.
^ «полукупола» . www.orchidpalms.com . Проверено 21 апреля 2018 г.
^ Перейти обратно: ^а ^б Выпуклая сегментохора Доктор Ричард Клитцинг, Симметрия: культура и наука, Vol. 11, № 1-4, 139-181, 2000 г.

Джонсон, С.В. Выпуклые многогранники с правильными гранями. Может. Дж. Математика. 18, 169–200, 1966.

Внешние ссылки

[1] «куполы» . www.orchidpalms.com . Проверено 21 апреля 2018 г.

[2] «полукупола» . www.orchidpalms.com . Проверено 21 апреля 2018 г.

[Segmentochora-3] Перейти обратно: ^а ^б Выпуклая сегментохора Доктор Ричард Клитцинг, Симметрия: культура и наука, Vol. 11, № 1-4, 139-181, 2000 г.

[1]

[2]

[3]