Нормальная форма Хомского

В формального языка теории , что контекстно-свободная грамматика G находится считается в нормальной форме Хомского (впервые описанной Ноамом Хомским ). ^{[ 1 ]} если все его производственные правила имеют вид: ^{[ 2 ]}^{[ 3 ]}

A → BC или

А → а или

S → е,

где A , B и C — нетерминальные символы , буква a — терминальный символ (символ, представляющий постоянное значение), S — начальный символ, а ε обозначает пустую строку . Кроме того, ни B, ни C не могут быть начальным символом , а третье правило продукции может появиться только в том случае, если ε находится в ( G ) , языке, созданном контекстно-свободной грамматикой G. L ^{[ 4 ]}^{: 92–93, 106}

Каждая грамматика в нормальной форме Хомского является контекстно-свободной, и наоборот, каждая контекстно-свободная грамматика может быть преобразована в эквивалентную . ^{[ примечание 1 ]} которая находится в нормальной форме Хомского и имеет размер не больше квадрата размера исходной грамматики.

Преобразование грамматики в нормальную форму Хомского

Чтобы преобразовать грамматику в нормальную форму Хомского, в определенном порядке применяется последовательность простых преобразований; это описано в большинстве учебников по теории автоматов . ^{[ 4 ]}^: 87–94^{[ 5 ]}^{[ 6 ]}^{[ 7 ]} Представленная здесь презентация соответствует Hopcroft, Ullman (1979), но адаптирована для использования названий преобразований из Lange, Leiß (2009). ^{[ 8 ]}^{[ примечание 2 ]} Каждое из следующих преобразований устанавливает одно из свойств, необходимых для нормальной формы Хомского.

СТАРТ: Удалите символ старта с правой стороны.

Введите новый начальный символ S ₀ и новое правило.

С ₀ → С ,

где S — предыдущий стартовый символ. Это не меняет созданный язык грамматики, и S ₀ не будет встречаться в правой части любого правила.

ТЕРМИН: Отменить правила с неодиночными терминалами

Чтобы устранить каждое правило

А → Х ₁ ... а ... Х _н

если терминальный символ a не является единственным символом в правой части, введем для каждого такого терминала новый нетерминальный символ N _a и новое правило

Н _а → а .

Изменить каждое правило

А → Х ₁ ... а ... Х _н

к

А → Икс ₁ … Н _а … Икс _п .

Если в правой части встречается несколько терминальных символов, одновременно замените каждый из них соответствующим нетерминальным символом. Это не меняет созданный язык грамматики. ^{[ 4 ]}^: 92

BIN: исключить правые части с более чем двумя нетерминалами.

Замените каждое правило

А → Х ₁ Х ₂ ... Х _н

с более чем двумя нетерминалами X ₁ ,..., X _n по правилам

А → Икс ₁ А ₁ ,

А ₁ → Икс ₂ А ₂ ,

... ,

А _{n -2} → X _{n -1} X _n ,

где A _i — новые нетерминальные символы. Опять же, это не меняет язык, созданный грамматикой. ^{[ 4 ]}^: 93

DEL: исключить ε-правила

ε-правило — это правило вида

А → е,

где A не является S ₀ , начальным символом грамматики.

Чтобы исключить все правила такого вида, сначала определите набор всех нетерминалов, которые выводят ε. Хопкрофт и Ульман (1979) называют такие нетерминалы обнуляемыми и вычисляют их следующим образом:

Если правило A → ε существует, то A допускает нулевое значение.
Если правило A → X ₁ ... X _n существует и каждое отдельное X _i допускает значение NULL, то A также допускает значение NULL.

Получите промежуточную грамматику, заменив каждое правило

А → Х ₁ ... Х _н

во всех версиях с опущенным некоторым обнуляемым X _i . Путем удаления в этой грамматике каждого ε-правила, если его левая часть не является начальным символом, получается преобразованная грамматика. ^{[ 4 ]}^: 90

Например, в следующей грамматике с начальным символом S ₀ ,

С ₀ → АбБ | С

Б → АА | переменного тока

С → б | с

А → а | е

нетерминал A , а следовательно, и , допускает значение NULL, в то время как ни C , ни S0 _B не являются. Таким образом, получается следующая промежуточная грамматика: ^{[ примечание 3 ]}

С ₀ → А б Б | А б Б | А б Б | А б Б | С

Б → АА | А А | А А | ε А | А С | И С

С → б | с

А → а | е

В этой грамматике все ε-правила «встроены в место вызова». ^{[ примечание 4 ]} На следующем этапе их можно удалить, получив грамматику:

С ₀ → АбБ | Аб | ББ | б | С

Б → АА | А | переменного тока | С

С → б | с

А → а

Эта грамматика создает тот же язык, что и исходный пример грамматики, а именно. { ab , aba , abaa , abab , abac , abb , abc , b , bab , bac , bb , bc , c }, но не имеет ε-правил.

БЛОК: отменить правила для отрядов

Единичное правило – это правило вида

А → Б ,

где A , B — нетерминальные символы. Чтобы удалить его, для каждого правила

Б → Икс ₁ ... Икс _п ,

где X ₁ ... X _n — строка нетерминалов и терминалов, добавьте правило

А → Х ₁ ... Х _н

кроме случаев, когда это правило единицы уже удалено (или удаляется). Пропуск нетерминального символа B в результирующей грамматике возможен из-за того, что является членом единичного замыкания нетерминального символа A. B ^{[ 9 ]}

Порядок преобразований

Взаимное сохранение
результатов трансформации
И Х	НАЧИНАТЬ	СРОК	БИН	ПРИНАДЛЕЖАЩИЙ	ЕДИНИЦА
Трансформация Х всегда сохраняет ( И ) соотв. может уничтожить ( N ) результат Y :
НАЧИНАТЬ
СРОК
БИН
ПРИНАДЛЕЖАЩИЙ
ЕДИНИЦА				( И ) ^*
^*UNIT сохраняет результат DEL если бы START был вызван раньше.

При выборе порядка применения указанных выше преобразований следует учитывать, что некоторые преобразования могут разрушить результат, достигнутый другими. Например, START повторно вводит правило единицы измерения, если оно применяется после UNIT . В таблице показано, какие заказы принимаются.

Более того, в худшем случае раздувание размера грамматики ^{[ примечание 5 ]} зависит от порядка преобразования. Использование | г | Чтобы обозначить размер исходной грамматики G , увеличение размера в худшем случае может варьироваться от | г | ² до 2 ^{2 |Г|}, в зависимости от используемого алгоритма преобразования. ^{[ 8 ]}^: 7 Увеличение размера грамматики зависит от порядка между DEL и BIN . Он может быть экспоненциальным, если DEL сначала выполняется , но в противном случае линейным. UNIT может привести к квадратичному увеличению размера грамматики. ^{[ 8 ]}^: 5 Порядки START , TERM , BIN , DEL , UNIT и START , BIN , DEL , UNIT , TERM приводят к наименьшему (то есть квадратичному) разрушению.

Пример

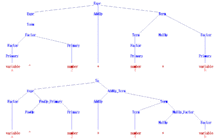
Следующая грамматика с начальным символом Expr описывает упрощенную версию набора всех синтаксически допустимых арифметических выражений в таких языках программирования, как C или Algol60 . И число , и переменная здесь для простоты считаются терминальными символами, поскольку во внешнем интерфейсе компилятора их внутренняя структура обычно не учитывается синтаксическим анализатором . Терминальный символ «^» обозначал возведение в степень в Алголе60.

Выражение	→ Срок	\| Выражение AddOp срока	\| AddOp Срок действия
Срок	→ Фактор	\| Срок MulOp Фактор
Фактор	→ Первичный	\| Фактор ^ Первичный
Начальный	→ номер	\| переменная	\| ( Экспр )
ДобавитьОп	→ +	\| −
МулОп	→ *	\| /

На этапе «СТАРТ» приведенного выше только правило S ₀ → Expr алгоритма преобразования в грамматику добавляется . После шага «TERM» грамматика выглядит так:

С ₀	→ Экспр
Выражение	→ Срок	\| Выражение AddOp срока	\| AddOp Срок действия
Срок	→ Фактор	\| Срок MulOp Фактор
Фактор	→ Первичный	\| Фактор PowOp Primary
Начальный	→ номер	\| переменная	\| Открыть выражение Закрыть
ДобавитьОп	→ +	\| −
МулОп	→ *	\| /
PowOp	→ ^
Открыть	→ (
Закрывать	→ )

После шага «BIN» получается следующая грамматика:

С ₀	→ Экспр
Выражение	→ Срок	\| Выражение AddOp_Term	\| AddOp Срок действия
Срок	→ Фактор	\| Срок MulOp_Factor
Фактор	→ Первичный	\| Фактор PowOp_Primary
Начальный	→ номер	\| переменная	\| Открыть Выражение_Закрыть
ДобавитьОп	→ +	\| −
МулОп	→ *	\| /
PowOp	→ ^
Открыть	→ (
Закрывать	→ )
АддОп_терм	→ AddOp Срок действия
MulOp_Factor	→ Многооперационный фактор
PowOp_Primary	→ PowOp Первичный
Выраж_Закрыть	→ Вывод Закрыть

Поскольку ε-правил нет, шаг «DEL» не меняет грамматику. После шага «UNIT» получается следующая грамматика, находящаяся в нормальной форме Хомского:

С ₀	→ номер	\| переменная	\| Открыть Выражение_Закрыть	\| Фактор PowOp_Primary	\| Срок MulOp_Factor	\| Выражение AddOp_Term	\| AddOp Срок действия
Выражение	→ номер	\| переменная	\| Открыть Выражение_Закрыть	\| Фактор PowOp_Primary	\| Срок MulOp_Factor	\| Выражение AddOp_Term	\| AddOp Срок действия
Срок	→ номер	\| переменная	\| Открыть Выражение_Закрыть	\| Фактор PowOp_Primary	\| Срок MulOp_Factor
Фактор	→ номер	\| переменная	\| Открыть Выражение_Закрыть	\| Фактор PowOp_Primary
Начальный	→ номер	\| переменная	\| Открыть Выражение_Закрыть
ДобавитьОп	→ +	\| −
МулОп	→ *	\| /
PowOp	→ ^
Открыть	→ (
Закрывать	→ )
АддОп_терм	→ AddOp Срок действия
MulOp_Factor	→ Многооперационный фактор
PowOp_Primary	→ PowOp Первичный
Выраж_Закрыть	→ Вывод Закрыть

N a _, представленные на шаге «TERM», — это PowOp , Open и Close . A i _, введенные на этапе «BIN», — это AddOp_Term , MulOp_Factor , PowOp_Primary и Expr_Close .

Альтернативное определение

Сокращенная форма Хомского

Другой способ ^{[ 4 ]}^: 92^{[ 10 ]} для определения нормальной формы Хомского:

Формальная грамматика находится в сокращенной форме Хомского , если все ее правила продукции имеют вид:

A\rightarrow \,BC

или

A\rightarrow \,a

,

где $A$ , $B$ и $C$ являются нетерминальными символами, а $a$ является терминальным символом . Используя это определение, $B$ или $C$ может быть стартовым символом. Только те контекстно-свободные грамматики, которые не генерируют пустую строку, могут быть преобразованы в сокращенную форму Хомского.

Флойд в нормальной форме

В письме, в котором он предложил термин « форма Бэкуса – Наура» (BNF), Дональд Э. Кнут подразумевал BNF, «синтаксис, в котором все определения имеют такую форму, можно сказать, что они находятся в «нормальной форме Флойда»».

\langle A\rangle ::=\,\langle B\rangle \mid \langle C\rangle

или

\langle A\rangle ::=\,\langle B\rangle \langle C\rangle

или

\langle A\rangle ::=\,a

,

где $\langle A\rangle$ , $\langle B\rangle$ и $\langle C\rangle$ являются нетерминальными символами, а $a$ является терминальным символом, потому что Роберт В. Флойд в 1961 году обнаружил, что любой синтаксис BNF можно преобразовать в приведенный выше. ^{[ 11 ]} Но он отказался от этого термина, «поскольку, несомненно, многие люди независимо использовали этот простой факт в своей работе, и этот момент является лишь второстепенным по отношению к основным соображениям заметки Флойда». ^{[ 12 ]} В заметке Флойда цитируется оригинальная статья Хомского 1959 года, а в письме Кнута — нет.

Приложение

Помимо своего теоретического значения, преобразование CNF используется в некоторых алгоритмах в качестве этапа предварительной обработки, например, в алгоритме CYK , восходящем анализе контекстно-свободных грамматик, и его варианте вероятностного CKY. ^{[ 13 ]}

См. также

Форма Бэкуса – Наура
Алгоритм CYK
Нормальная форма Грейбаха
Курода нормальная форма
Лемма о накачке для контекстно-свободных языков - ее доказательство основано на нормальной форме Хомского.

Примечания

^ то есть тот, который производит тот же язык
^ Например, Хопкрофт, Ульман (1979) объединили TERM и BIN в одно преобразование.
^ указывает на сохраненный и опущенный нетерминал N с помощью Н и Н соответственно
^ Если бы в грамматике было правило S ₀ → ε, ее нельзя было бы «встроить», поскольку в ней не было «сайтов вызова». Поэтому его нельзя было удалить на следующем этапе.
^ т.е. длина письма, измеряемая в символах

Ссылки

^ Хомский, Ноам (1959). «О некоторых формальных свойствах грамматик». Информация и контроль . 2 (2): 137–167. дои : 10.1016/S0019-9958(59)90362-6 . Здесь: Раздел 6, стр. 152 и далее.
^ Д'Антони, Лорис. «Страница 7, Лекция 9: Алгоритмы синтаксического анализа снизу вверх» (PDF) . CS536-S21 Введение в языки программирования и компиляторы . Университет Висконсин-Мэдисон. Архивировано (PDF) из оригинала 19 июля 2021 г.
^ Сипсер, Майкл (2006). Введение в теорию вычислений (2-е изд.). Бостон: Технология курса Томсона. Определение 2.8. ISBN 0-534-95097-3 . OCLC 58544333 .
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж Хопкрофт, Джон Э.; Уллман, Джеффри Д. (1979). Введение в теорию автоматов, языки и вычисления . Ридинг, Массачусетс: Издательство Addison-Wesley. ISBN 978-0-201-02988-8 .
^ Хопкрофт, Джон Э.; Мотвани, Раджив; Уллман, Джеффри Д. (2006). Введение в теорию автоматов, языки и вычисления (3-е изд.). Аддисон-Уэсли. ISBN 978-0-321-45536-9 . Раздел 7.1.5, стр.272
^ Рич, Элейн (2007). «11.8 Нормальные формы». Автоматы, вычислимость и сложность: теория и приложения (PDF) (1-е изд.). Прентис-Холл. п. 169. ИСБН 978-0132288064 . Архивировано из оригинала (PDF) 17 января 2023 г.
^ Вегенер, Инго (1993). Теоретическая информатика. Алгоритмически-ориентированное введение . Руководства и монографии по информатике (на немецком языке). Штутгарт: Б. Г. Тойбнер. ISBN 978-3-519-02123-0 . Раздел 6.2 «Нормальная форма Хомского для контекстно-свободных грамматик», с. 149-152
^ Перейти обратно: ^а ^б ^с Ланге, Мартин; Лейсс, Ганс (2009). «В CNF или не в CNF? Эффективная, но презентабельная версия алгоритма CYK» (PDF) . Информатика Дидактика . 8 . Архивировано (PDF) из оригинала 19 июля 2011 г.
^ Эллисон, Чарльз Д. (2022). Основы вычислений: доступное введение в автоматы и формальные языки . Fresh Sources, Inc. с. 176. ИСБН 9780578944173 .
^ Хопкрофт и др. (2006) ^{[ нужна страница ]}
^ Флойд, Роберт В. (1961). «Заметка о математической индукции в грамматиках фразовых структур» (PDF) . Информация и контроль . 4 (4): 353–358. дои : 10.1016/S0019-9958(61)80052-1 . Архивировано (PDF) из оригинала 05 марта 2021 г. Здесь: стр.354
^ Кнут, Дональд Э. (декабрь 1964 г.). «Нормальная форма Бэкуса против формы Бэкуса-Наура» . Коммуникации АКМ . 7 (12): 735–736. дои : 10.1145/355588.365140 . S2CID 47537431 .
^ Юрафский, Дэниел; Мартин, Джеймс Х. (2008). Обработка речи и языка (2-е изд.). Пирсон Прентис Холл. п. 465. ИСБН 978-0-13-187321-6 .

Дальнейшее чтение

Коул, Ричард. Преобразование CFG в CNF (нормальная форма Хомского) , 17 октября 2007 г. (pdf) — используется порядок TERM, BIN, START, DEL, UNIT.
Джон Мартин (2003). Введение в языки и теорию вычислений . МакГроу Хилл. ISBN 978-0-07-232200-2 . (Страницы 237–240 раздела 6.6: упрощенные формы и нормальные формы.)
Майкл Сипсер (1997). Введение в теорию вычислений . Издательство ПВС. ISBN 978-0-534-94728-6 . (Страницы 98–101 раздела 2.1: контекстно-свободные грамматики. Страница 156.)
Чарльз Д. Эллисон (2021 г.) (20 августа 2021 г.). Основы информатики: доступное введение в формальный язык . Fresh Sources, Inc. ISBN 9780578944173 . {{cite book}}: CS1 maint: числовые имена: список авторов ( ссылка ) (страницы 171-183 раздела 7.1: Нормальная форма Хомского)
Сипсер, Майкл. Введение в теорию вычислений, 2-е издание.
Александр Медуна (6 декабря 2012 г.). Автоматы и языки: теория и приложения . Springer Science & Business Media. ISBN 978-1-4471-0501-5 .

[5] то есть тот, который производит тот же язык

[10] Например, Хопкрофт, Ульман (1979) объединили TERM и BIN в одно преобразование.

[11] указывает на сохраненный и опущенный нетерминал N с помощью Н и Н соответственно

[12] Если бы в грамматике было правило S ₀ → ε, ее нельзя было бы «встроить», поскольку в ней не было «сайтов вызова». Поэтому его нельзя было удалить на следующем этапе.

[14] т.е. длина письма, измеряемая в символах

[1] Хомский, Ноам (1959). «О некоторых формальных свойствах грамматик». Информация и контроль . 2 (2): 137–167. дои : 10.1016/S0019-9958(59)90362-6 . Здесь: Раздел 6, стр. 152 и далее.

[2] Д'Антони, Лорис. «Страница 7, Лекция 9: Алгоритмы синтаксического анализа снизу вверх» (PDF) . CS536-S21 Введение в языки программирования и компиляторы . Университет Висконсин-Мэдисон. Архивировано (PDF) из оригинала 19 июля 2021 г.

[3] Сипсер, Майкл (2006). Введение в теорию вычислений (2-е изд.). Бостон: Технология курса Томсона. Определение 2.8. ISBN 0-534-95097-3 . OCLC 58544333 .

[Hopcroft.Ullman.1979-4] Перейти обратно: ^а ^б ^с ^д ^и ^ж Хопкрофт, Джон Э.; Уллман, Джеффри Д. (1979). Введение в теорию автоматов, языки и вычисления . Ридинг, Массачусетс: Издательство Addison-Wesley. ISBN 978-0-201-02988-8 .

[6] Хопкрофт, Джон Э.; Мотвани, Раджив; Уллман, Джеффри Д. (2006). Введение в теорию автоматов, языки и вычисления (3-е изд.). Аддисон-Уэсли. ISBN 978-0-321-45536-9 . Раздел 7.1.5, стр.272

[7] Рич, Элейн (2007). «11.8 Нормальные формы». Автоматы, вычислимость и сложность: теория и приложения (PDF) (1-е изд.). Прентис-Холл. п. 169. ИСБН 978-0132288064 . Архивировано из оригинала (PDF) 17 января 2023 г.

[8] Вегенер, Инго (1993). Теоретическая информатика. Алгоритмически-ориентированное введение . Руководства и монографии по информатике (на немецком языке). Штутгарт: Б. Г. Тойбнер. ISBN 978-3-519-02123-0 . Раздел 6.2 «Нормальная форма Хомского для контекстно-свободных грамматик», с. 149-152

[Lange.Leis.2009-9] Перейти обратно: ^а ^б ^с Ланге, Мартин; Лейсс, Ганс (2009). «В CNF или не в CNF? Эффективная, но презентабельная версия алгоритма CYK» (PDF) . Информатика Дидактика . 8 . Архивировано (PDF) из оригинала 19 июля 2011 г.

[13] Эллисон, Чарльз Д. (2022). Основы вычислений: доступное введение в автоматы и формальные языки . Fresh Sources, Inc. с. 176. ИСБН 9780578944173 .

[15] Хопкрофт и др. (2006) ^{[ нужна страница ]}

[16] Флойд, Роберт В. (1961). «Заметка о математической индукции в грамматиках фразовых структур» (PDF) . Информация и контроль . 4 (4): 353–358. дои : 10.1016/S0019-9958(61)80052-1 . Архивировано (PDF) из оригинала 05 марта 2021 г. Здесь: стр.354

[knuth1964-17] Кнут, Дональд Э. (декабрь 1964 г.). «Нормальная форма Бэкуса против формы Бэкуса-Наура» . Коммуникации АКМ . 7 (12): 735–736. дои : 10.1145/355588.365140 . S2CID 47537431 .

[18] Юрафский, Дэниел; Мартин, Джеймс Х. (2008). Обработка речи и языка (2-е изд.). Пирсон Прентис Холл. п. 465. ИСБН 978-0-13-187321-6 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ примечание 1 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ примечание 2 ]

[ примечание 3 ]

[ примечание 4 ]

[ 9 ]

[ примечание 5 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]