Формальная грамматика

Формальная грамматика описывает, какие строки из алфавита формального языка языка действительны в соответствии с синтаксисом . Грамматика не описывает значение строк или то, что с ними можно делать в каком бы то ни было контексте — только их форму. Формальная грамматика определяется как набор правил производства таких строк на формальном языке.

Теория формального языка — дисциплина, изучающая формальные грамматики и языки, — раздел прикладной математики . Его приложения находят в теоретической информатике , теоретической лингвистике , формальной семантике , математической логике и других областях.

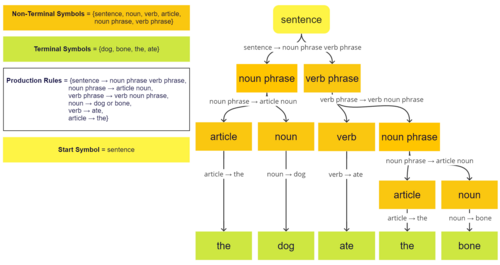
Формальная грамматика — это набор правил перезаписи строк, а также «начальный символ», с которого начинается перезапись. Поэтому грамматику обычно рассматривают как генератор языка. Однако иногда его также можно использовать в качестве основы для « распознавателя » — вычислительной функции, которая определяет, принадлежит ли данная строка языку или она грамматически неверна. Для описания таких распознавателей формальная теория языка использует отдельные формализмы, известные как теория автоматов . Одним из интересных результатов теории автоматов является то, что невозможно спроектировать распознаватель для некоторых формальных языков. ^[1] Синтаксический анализ — это процесс распознавания высказывания (строки на естественных языках) путем его разбиения на набор символов и анализа каждого из них на соответствие грамматике языка. В большинстве языков значения высказываний структурированы в соответствии с их синтаксисом — практика, известная как композиционная семантика . В результате первый шаг к описанию значения высказывания в языке — разбить его на части и посмотреть на его анализируемую форму (известную как дерево разбора в информатике и как его глубокая структура в порождающей грамматике ).

Вводный пример

Грамматика в основном состоит из набора продукционных правил , правил перезаписи для преобразования строк. Каждое правило определяет замену определенной строки (ее левой части ) на другую (ее правой части ). Правило можно применить к каждой строке, содержащей ее левую часть, и создать строку, в которой вхождение этой левой части заменено ее правой частью.

В отличие от системы полу-Туэ , которая полностью определяется этими правилами, грамматика дополнительно различает два вида символов: нетерминальные и терминальные символы ; каждая левая часть должна содержать хотя бы один нетерминальный символ. Также выделяется специальный нетерминальный символ, называемый стартовым символом .

Язык, порожденный грамматикой, определяется как набор всех строк без каких-либо нетерминальных символов, которые могут быть сгенерированы из строки, состоящей из одного начального символа, путем (возможно, повторяющегося) применения ее правил любым возможным способом.Если существуют существенно разные способы генерации одной и той же строки, грамматика называется неоднозначной .

В следующих примерах терминальными символами являются a и b , а начальным символом S. —

Пример 1

Предположим, у нас есть следующие правила производства:

1.

S\rightarrow aSb

2.

S\rightarrow ba

затем мы начинаем с S и можем выбрать правило, которое будет применяться к нему. Если мы выберем правило 1, мы получим строку aSb . Если затем мы снова выберем правило 1, мы заменим S на aSb и получим строку aaSbb . Если мы теперь выберем правило 2, мы заменим S на ba и получим строку aababb , и все готово. Мы можем записать эту серию выборов более кратко, используя символы: $S\Rightarrow aSb\Rightarrow aaSbb\Rightarrow aababb$ .

Язык грамматики – это бесконечное множество $\{a^{n}bab^{n}\mid n\geq 0\}=\{ba,abab,aababb,aaababbb,\dotsc \}$ , где $a^{k}$ является $a$ повторенный $k$ раз (и $n$ в частности, представляет собой количество применений производственного правила 1). Эта грамматика является контекстно-свободной (только отдельные нетерминалы появляются в левой части) и однозначной.

Примеры 2 и 3

Предположим, что вместо этого действуют следующие правила:

1.

S\rightarrow a

2.

S\rightarrow SS

3.

aSa\rightarrow b

Эта грамматика не является контекстно-свободной из-за правила 3 и неоднозначна из-за множества способов использования правила 2 для генерации последовательностей $S$ с.

Однако генерируемый им язык представляет собой просто набор всех непустых строк, состоящих из $a$ и/или $b$ с.Это легко увидеть: чтобы создать $b$ из $S$ , используйте правило 2 дважды, чтобы сгенерировать $SSS$ , затем правило 1 дважды и правило 3 один раз, чтобы получить $b$ . Это означает, что мы можем генерировать произвольные непустые последовательности $S$ s, а затем замените каждый из них на $a$ или $b$ как нам заблагорассудится.

Альтернативно тот же самый язык может быть создан с помощью контекстно-свободной, однозначной грамматики; например, обычная грамматика с правилами

1.

S\rightarrow aS

2.

S\rightarrow bS

3.

S\rightarrow a

4.

S\rightarrow b

Формальное определение

Синтаксис грамматик

В классической формализации порождающих грамматик, впервые предложенной Ноамом Хомским в 1950-х годах, ^[2]^[3] грамматика G состоит из следующих компонентов:

Конечное множество N , нетерминальных символов не пересекающееся со строками, образованными G. из
Конечное множество $\Sigma$ терминальных символов , не пересекающихся с N .
Конечное множество P правил производства , каждое правило вида

(\Sigma \cup N)^{*}N(\Sigma \cup N)^{*}\rightarrow (\Sigma \cup N)^{*}

где

{*}

является звездным оператором Клини и

\cup

обозначает объединение множеств . То есть каждое продукционное правило отображается из одной строки символов в другую, где первая строка («голова») содержит произвольное количество символов, при условии, что хотя бы один из них является нетерминалом. В случае, если вторая строка («тело») состоит исключительно из пустой строки , т. е. вообще не содержит символов, ее можно обозначить специальным обозначением (часто

\Lambda

, е или

\epsilon

), чтобы избежать путаницы.

Выдающийся символ $S\in N$ это начальный символ , также называемый символом предложения .

Грамматика формально определяется как кортеж $(N,\Sigma ,P,S)$ . Такую формальную грамматику часто называют системой переписывания или грамматикой фразовой структуры . в литературе ^[4]^[5]

Некоторые математические конструкции, касающиеся формальных грамматик

Работа грамматики может быть определена в терминах отношений со строками:

Учитывая грамматику $G=(N,\Sigma ,P,S)$ , бинарное отношение ${\underset {G}{\Rightarrow }}$ (произносится как «G выводится за один шаг») на строках в $(\Sigma \cup N)^{*}$ определяется:
$x{\underset {G}{\Rightarrow }}y\iff \exists u,v,p,q\in (\Sigma \cup N)^{*}:(x=upv)\wedge (p\rightarrow q\in P)\wedge (y=uqv)$
отношение ${\overset {*}{\underset {G}{\Rightarrow }}}$ (произносится как G, выводится за ноль или более шагов ) определяется как рефлексивное транзитивное замыкание ${\underset {G}{\Rightarrow }}$
форма предложения является членом $(\Sigma \cup N)^{*}$ который можно получить за конечное число шагов из начального символа $S$ ; то есть форма предложения является членом $\left\{w\in (\Sigma \cup N)^{*}\mid S{\overset {*}{\underset {G}{\Rightarrow }}}w\right\}$ . Предлогательная форма, не содержащая нетерминальных символов (т. е. являющаяся членом $\Sigma ^{*}$ ) называется предложением . ^[6]
язык $G$ , обозначенный как ${\boldsymbol {L}}(G)$ , определяется как набор предложений, построенных $G$ .

Грамматика $G=(N,\Sigma ,P,S)$ фактически является системой полу-Туэ $(N\cup \Sigma ,P)$ , переписывая строки точно таким же образом; единственное отличие состоит в том, что мы выделяем конкретные нетерминальные символы, которые должны быть переписаны в правилах перезаписи, и нас интересуют только переписывания из обозначенного начального символа. $S$ к строкам без нетерминальных символов.

Пример

В этих примерах формальные языки указываются с использованием нотации set-builder .

Рассмотрим грамматику $G$ где $N=\left\{S,B\right\}$ , $\Sigma =\left\{a,b,c\right\}$ , $S$ является стартовым символом, и $P$ состоит из следующих правил производства:

1.

S\rightarrow aBSc

2.

S\rightarrow abc

3.

Ba\rightarrow aB

4.

Bb\rightarrow bb

Эта грамматика определяет язык $L(G)=\left\{a^{n}b^{n}c^{n}\mid n\geq 1\right\}$ где $a^{n}$ обозначает строку из n последовательных $a$ х. Таким образом, язык — это набор строк, состоящих из 1 или более $a$ s, за которыми следует такое же количество $b$ s, за которыми следует такое же количество $c$ х.

Некоторые примеры вывода строк в $L(G)$ являются:

${\boldsymbol {S}}{\underset {2}{\Rightarrow }}{\boldsymbol {abc}}$
${\begin{aligned}{\boldsymbol {S}}&{\underset {1}{\Rightarrow }}{\boldsymbol {aBSc}}\\&{\underset {2}{\Rightarrow }}aB{\boldsymbol {abc}}c\\&{\underset {3}{\Rightarrow }}a{\boldsymbol {aB}}bcc\\&{\underset {4}{\Rightarrow }}aa{\boldsymbol {bb}}cc\end{aligned}}$
${\begin{aligned}{\boldsymbol {S}}&{\underset {1}{\Rightarrow }}{\boldsymbol {aBSc}}{\underset {1}{\Rightarrow }}aB{\boldsymbol {aBSc}}c\\&{\underset {2}{\Rightarrow }}aBaB{\boldsymbol {abc}}cc\\&{\underset {3}{\Rightarrow }}a{\boldsymbol {aB}}Babccc{\underset {3}{\Rightarrow }}aaB{\boldsymbol {aB}}bccc{\underset {3}{\Rightarrow }}aa{\boldsymbol {aB}}Bbccc\\&{\underset {4}{\Rightarrow }}aaaB{\boldsymbol {bb}}ccc{\underset {4}{\Rightarrow }}aaa{\boldsymbol {bb}}bccc\end{aligned}}$

(По обозначениям:

P{\underset {i}{\Rightarrow }}Q

гласит: «Строка

P

порождает строку

Q

посредством продукции

i

», а сгенерированная часть каждый раз выделяется жирным шрифтом.)

Иерархия Хомского

Когда Ноам Хомский впервые формализовал порождающие грамматики в 1956 году, ^[2] он классифицировал их по типам, известным теперь как иерархия Хомского . Разница между этими типами заключается в том, что они имеют все более строгие правила производства и, следовательно, могут выражать меньше формальных языков. Двумя важными типами являются контекстно-свободные грамматики (тип 2) и регулярные грамматики (тип 3). Языки, которые можно описать с помощью такой грамматики, называются контекстно-свободными языками и регулярными языками соответственно. Хотя эти два ограниченных типа грамматик гораздо менее мощны, чем неограниченные грамматики (Тип 0), которые фактически могут выражать любой язык, который может быть принят машиной Тьюринга , они используются чаще всего, поскольку для них можно эффективно реализовать синтаксические анализаторы. ^[7] Например, все обычные языки могут распознаваться конечным автоматом , а для полезных подмножеств контекстно-свободных грамматик существуют хорошо известные алгоритмы для создания эффективных анализаторов LL и анализаторов LR для распознавания соответствующих языков, генерируемых этими грамматиками.

Контекстно-свободные грамматики

Контекстно -свободная грамматика — это грамматика, в которой левая часть каждого продукционного правила состоит только из одного нетерминального символа. Это ограничение нетривиально; не все языки могут быть созданы с помощью контекстно-свободных грамматик. Те, которые могут, называются контекстно-свободными языками .

Язык $L(G)=\left\{a^{n}b^{n}c^{n}\mid n\geq 1\right\}$ определенный выше, не является контекстно-свободным языком, и это можно строго доказать с помощью леммы о накачке для контекстно-свободных языков , но, например, язык $\left\{a^{n}b^{n}\mid n\geq 1\right\}$ (минимум 1 $a$ за которым следует такое же количество $b$ 's) является контекстно-свободным, поскольку его можно определить с помощью грамматики $G_{2}$ с $N=\left\{S\right\}$ , $\Sigma =\left\{a,b\right\}$ , $S$ стартовый символ и следующие правила производства:

1.

S\rightarrow aSb

2.

S\rightarrow ab

Контекстно-свободный язык можно распознать в $O(n^{3})$ время ( см. обозначение Big O ) с помощью алгоритма, такого как распознаватель Эрли . То есть для каждого контекстно-свободного языка можно построить машину, которая принимает на вход строку и определяет в $O(n^{3})$ время, является ли строка членом языка, где $n$ это длина строки. ^[8] Детерминированные контекстно-свободные языки — это подмножество контекстно-свободных языков, которые можно распознать за линейное время. ^[9] Существуют различные алгоритмы, ориентированные либо на этот набор языков, либо на его подмножество.

Регулярные грамматики

В обычных грамматиках левая часть снова представляет собой только один нетерминальный символ, но теперь правая часть также ограничена. Правая часть может быть пустой строкой, или одним терминальным символом, или одним терминальным символом, за которым следует нетерминальный символ, но не более того. (Иногда используется более широкое определение: можно разрешить более длинные строки терминалов или отдельные нетерминалы без чего-либо еще, что упрощает обозначение языков , в то же время определяя один и тот же класс языков.)

Язык $\left\{a^{n}b^{n}\mid n\geq 1\right\}$ определенное выше, не является регулярным, но язык $\left\{a^{n}b^{m}\mid m,n\geq 1\right\}$ (минимум 1 $a$ за которым следует хотя бы 1 $b$ , где числа могут быть разными) есть, как это можно определить с помощью грамматики $G_{3}$ с $N=\left\{S,A,B\right\}$ , $\Sigma =\left\{a,b\right\}$ , $S$ стартовый символ и следующие правила производства:

$S\rightarrow aA$
$A\rightarrow aA$
$A\rightarrow bB$
$B\rightarrow bB$
$B\rightarrow \epsilon$

Все языки, порожденные обычной грамматикой, можно распознать в $O(n)$ время с помощью конечного автомата. Хотя на практике регулярные грамматики обычно выражаются с использованием регулярных выражений , некоторые формы регулярных выражений, используемые на практике, не создают строго регулярные языки и не демонстрируют линейной эффективности распознавания из-за этих отклонений.

Другие формы порождающих грамматик

Многие расширения и вариации исходной иерархии формальных грамматик Хомского были разработаны как лингвистами, так и учеными-компьютерщиками, обычно либо для того, чтобы увеличить их выразительную силу, либо для того, чтобы облегчить их анализ или синтаксический анализ. Некоторые формы разработанных грамматик включают:

Грамматики, примыкающие к деревьям, повышают выразительность традиционных генеративных грамматик, позволяя правилам перезаписи работать с деревьями синтаксического анализа, а не только со строками. ^[10]
Аффиксные грамматики ^[11] и атрибутивные грамматики ^[12]^[13] позволяют дополнять правила перезаписи семантическими атрибутами и операциями, полезными как для повышения выразительности грамматики, так и для создания практических инструментов языкового перевода.

Рекурсивные грамматики

Рекурсивная грамматика — это грамматика, содержащая рекурсивные производственные правила . Например, грамматика контекстно-свободного языка является леворекурсивной, если существует нетерминальный символ A , который можно пропустить через правила производства для создания строки, в которой A является самым левым символом. ^[14] Примером рекурсивной грамматики является предложение внутри предложения, разделенное двумя запятыми. ^[15] Все типы грамматик в иерархии Хомского могут быть рекурсивными.

Аналитические грамматики

Хотя существует огромное количество литературы по алгоритмам синтаксического анализа , большинство этих алгоритмов предполагают, что анализируемый язык изначально описывается посредством порождающей формальной грамматики, и что цель состоит в том, чтобы преобразовать эту порождающую грамматику в работающий синтаксический анализатор. Строго говоря, порождающая грамматика никак не соответствует алгоритму, используемому для разбора языка, и различные алгоритмы имеют разные ограничения на форму продукционных правил, которые считаются корректными.

Альтернативный подход состоит в том, чтобы формализовать язык в первую очередь с помощью аналитической грамматики, которая более непосредственно соответствует структуре и семантике синтаксического анализатора языка. Примеры формализмов аналитической грамматики включают следующее:

Язык нисходящего синтаксического анализа (TDPL): крайне минималистичный аналитический грамматический формализм, разработанный в начале 1970-х годов для изучения поведения нисходящих синтаксических анализаторов . ^[16]
Грамматики связей : форма аналитической грамматики, разработанная для лингвистики , которая выводит синтаксическую структуру путем изучения позиционных отношений между парами слов. ^[17]^[18]
Грамматики выражений синтаксического анализа (PEG): более позднее обобщение TDPL, разработанное с учетом практических в выразительности потребностей языков программирования и авторов компиляторов . ^[19]

См. также

Ссылки

^ Медуна, Александр (2014), Формальные языки и вычисления: модели и их приложения , CRC Press, стр. 233, ISBN 9781466513457 . Дополнительную информацию по этой теме см. в разделе «Неразрешимая проблема» .
^ Перейти обратно: ^а ^б Хомский, Ноам (сентябрь 1956 г.). «Три модели описания языка». IRE Транзакции по теории информации . 2 (3): 113–124. дои : 10.1109/TIT.1956.1056813 . S2CID 19519474 .
^ Хомский, Ноам (1957). Синтаксические структуры . Гаага: Мутон .
^ Гинзбург, Сеймур (1975). Алгебраические и теоретико-автоматные свойства формальных языков . Северная Голландия. стр. 8–9. ISBN 978-0-7204-2506-2 .
^ Харрисон, Майкл А. (1978). Введение в теорию формального языка . Ридинг, Массачусетс: Издательство Addison-Wesley. п. 13. ISBN 978-0-201-02955-0 .
^ Формы предложений. Архивировано 13 ноября 2019 г. в Wayback Machine , Контекстно-свободные грамматики, Дэвид Матушек.
^ Грюн, Дик и Джейкобс, Сериэль Х., Методы синтаксического анализа – Практическое руководство , Эллис Хорвуд, Англия, 1990.
^ Эрли, Джей, « Эффективный алгоритм контекстно-свободного анализа, заархивировано 19 мая 2020 г. в Wayback Machine », Communications of the ACM , Vol. 13 № 2, стр. 94–102, февраль 1970 г.
^ Кнут, DE (июль 1965 г.). «О переводе языков слева направо». Информация и контроль . 8 (6): 607–639. дои : 10.1016/S0019-9958(65)90426-2 .
^ Джоши, Аравинд К. и др. , « Древовидные дополнительные грамматики », Journal of Computer Systems Science , Vol. 10 № 1, стр. 136–163, 1975.
^ Костер, Корнелис Х.А., «Аффиксные грамматики», в реализации ALGOL 68 , North Holland Publishing Company, Амстердам, стр. 95-109, 1971.
^ Кнут, Дональд Э., « Семантика контекстно-свободных языков », Теория математических систем , Vol. 2 № 2, стр. 127–145, 1968.
^ Кнут, Дональд Э., «Семантика контекстно-свободных языков (коррекция),» Теория математических систем , Vol. 5 № 1, стр. 95-96, 1971.
↑ Заметки по теории формального языка и синтаксическому анализу. Архивировано 28 августа 2017 г. в Wayback Machine , Джеймс Пауэр, факультет компьютерных наук Национального университета Ирландии, Мейнут Мейнут, графство Килдэр, Ирландия. JPR02
^ Боренштейн, Сет (27 апреля 2006 г.). «Певчие птицы тоже понимают грамматику» . Северо-Западный Вестник . п. 2 – через Newspapers.com.
^ Бирман, Александр, Схема признания TMG , докторская диссертация, Принстонский университет, факультет электротехники, февраль 1970 г.
^ Слитор, Дэниел Д. и Темперли, Дэви, « Разбор английского языка с помощью грамматики ссылок », Технический отчет CMU-CS-91-196, Компьютерные науки Университета Карнеги-Меллона, 1991.
^ Слиатор, Дэниел Д. и Темперли, Дэви, «Разбор английского языка с помощью грамматики ссылок», Третий международный семинар по технологиям синтаксического анализа , 1993. (Пересмотренная версия приведенного выше отчета.)
^ Форд, Брайан, Анализ Packrat: практический алгоритм линейного времени с обратным отслеживанием , магистерская диссертация, Массачусетский технологический институт, сентябрь 2002 г.

Внешние ссылки

[1] Медуна, Александр (2014), Формальные языки и вычисления: модели и их приложения , CRC Press, стр. 233, ISBN 9781466513457 . Дополнительную информацию по этой теме см. в разделе «Неразрешимая проблема» .

[Chomsky1956-2] Перейти обратно: ^а ^б Хомский, Ноам (сентябрь 1956 г.). «Три модели описания языка». IRE Транзакции по теории информации . 2 (3): 113–124. дои : 10.1109/TIT.1956.1056813 . S2CID 19519474 .

[Chomsky1957-3] Хомский, Ноам (1957). Синтаксические структуры . Гаага: Мутон .

[4] Гинзбург, Сеймур (1975). Алгебраические и теоретико-автоматные свойства формальных языков . Северная Голландия. стр. 8–9. ISBN 978-0-7204-2506-2 .

[5] Харрисон, Майкл А. (1978). Введение в теорию формального языка . Ридинг, Массачусетс: Издательство Addison-Wesley. п. 13. ISBN 978-0-201-02955-0 .

[6] Формы предложений. Архивировано 13 ноября 2019 г. в Wayback Machine , Контекстно-свободные грамматики, Дэвид Матушек.

[Grune&Jacobs1990-7] Грюн, Дик и Джейкобс, Сериэль Х., Методы синтаксического анализа – Практическое руководство , Эллис Хорвуд, Англия, 1990.

[Earley1970-8] Эрли, Джей, « Эффективный алгоритм контекстно-свободного анализа, заархивировано 19 мая 2020 г. в Wayback Machine », Communications of the ACM , Vol. 13 № 2, стр. 94–102, февраль 1970 г.

[9] Кнут, DE (июль 1965 г.). «О переводе языков слева направо». Информация и контроль . 8 (6): 607–639. дои : 10.1016/S0019-9958(65)90426-2 .

[JoshiEtAl1975-10] Джоши, Аравинд К. и др. , « Древовидные дополнительные грамматики », Journal of Computer Systems Science , Vol. 10 № 1, стр. 136–163, 1975.

[Koster1971-11] Костер, Корнелис Х.А., «Аффиксные грамматики», в реализации ALGOL 68 , North Holland Publishing Company, Амстердам, стр. 95-109, 1971.

[Knuth1968-12] Кнут, Дональд Э., « Семантика контекстно-свободных языков », Теория математических систем , Vol. 2 № 2, стр. 127–145, 1968.

[Knuth1971-13] Кнут, Дональд Э., «Семантика контекстно-свободных языков (коррекция),» Теория математических систем , Vol. 5 № 1, стр. 95-96, 1971.

[14] Заметки по теории формального языка и синтаксическому анализу. Архивировано 28 августа 2017 г. в Wayback Machine , Джеймс Пауэр, факультет компьютерных наук Национального университета Ирландии, Мейнут Мейнут, графство Килдэр, Ирландия. JPR02

[15] Боренштейн, Сет (27 апреля 2006 г.). «Певчие птицы тоже понимают грамматику» . Северо-Западный Вестник . п. 2 – через Newspapers.com.

[Birman1970-16] Бирман, Александр, Схема признания TMG , докторская диссертация, Принстонский университет, факультет электротехники, февраль 1970 г.

[Sleater&Temperly1991-17] Слитор, Дэниел Д. и Темперли, Дэви, « Разбор английского языка с помощью грамматики ссылок », Технический отчет CMU-CS-91-196, Компьютерные науки Университета Карнеги-Меллона, 1991.

[Sleater&Temperly1993-18] Слиатор, Дэниел Д. и Темперли, Дэви, «Разбор английского языка с помощью грамматики ссылок», Третий международный семинар по технологиям синтаксического анализа , 1993. (Пересмотренная версия приведенного выше отчета.)

[19] Форд, Брайан, Анализ Packrat: практический алгоритм линейного времени с обратным отслеживанием , магистерская диссертация, Массачусетский технологический институт, сентябрь 2002 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]