Слерп

В компьютерной графике slerp — это сокращение от сферической линейной интерполяции , введенной Кеном Шумейком. ^[1] в контексте кватернионной интерполяции с целью анимации трехмерного вращения . единичного радиуса Это относится к движению с постоянной скоростью по дуге большого круга с учетом концов и параметра интерполяции от 0 до 1.

Геометрический слерп

У Слерпа есть геометрическая формула, независимая от кватернионов и размерности пространства, в которое встроена дуга. Эта формула, представляющая собой симметричную взвешенную сумму, приписанную Гленну Дэвису, основана на том факте, что любая точка кривой должна представлять собой линейную комбинацию концов. Пусть p ₀ и p ₁ — первая и последняя точки дуги, и пусть t — параметр, 0 ≤ t ≤ 1 . Вычислите Ω как угол, образованный дугой, так что cos Ω = p ₀ ⋅ p ₁ , n -мерное скалярное произведение единичных векторов от начала координат до концов. Тогда геометрическая формула будет

\operatorname {slerp} (p_{0},p_{1};t)={\frac {\sin {[(1-t)\Omega }]}{\sin \Omega }}p_{0}+{\frac {\sin[t\Omega ]}{\sin \Omega }}p_{1}.

Симметрия заключается в том, что slerp( p ₀ , p ₁ ; t ) = slerp ( p ₁ , p ₀ ; 1 − t ) . В пределе при Ω → 0 эта формула сводится к соответствующей симметричной формуле для линейной интерполяции

\operatorname {lerp} (p_{0},p_{1};t)=(1-t)p_{0}+tp_{1}.

По сути, траектория скольжения представляет собой сферический геометрический эквивалент пути вдоль отрезка линии на плоскости; большой круг — это сферическая геодезическая .

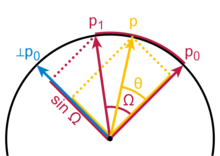
Более известен, чем общая формула Слерпа, случай, когда конечные векторы перпендикулярны, и в этом случае формула имеет вид p ₀ cos θ + p ₁ sin θ . Полагая θ = t $π$ /2 и применяя тригонометрическое тождество cos θ = sin( $π$ /2 − θ ) , получаем формулу Слерпа. Множитель 1/sin Ω в общей формуле является нормализацией, поскольку вектор p ₁ под углом Ω к p ₀ проектируется на перпендикуляр ⊥ p ₀ длиной всего лишь sin Ω .

Некоторые частные случаи slerp допускают более эффективные вычисления. Когда дугу окружности необходимо нарисовать в растровом изображении, предпочтительным методом является некоторая вариация Брезенхема окружности алгоритма . Оценка при значениях специальных параметров 0 и 1 тривиально дает p ₀ и p ₁ соответственно; и деление пополам, оценка при ⁠ 1/2 + ⁠ , упрощается до ( p ₀ , p ₁ )/2 нормализуется. Другой особый случай, распространенный в анимации, — это вычисление с фиксированными концами и равными параметрическими шагами. Если p _{k −1} и p _k — два последовательных значения, и если c — удвоенное их скалярное произведение (постоянное для всех шагов), то следующее значение p _{k +1} — это отражение p _{k +1} = cp _k − p _{к -1} .

Кватернионный слерп

Когда slerp применяется к единичным кватернионам , путь кватерниона отображается в путь посредством трехмерных вращений стандартным способом . Эффект заключается в вращении с равномерной угловой скоростью вокруг фиксированной оси вращения . Когда начальной конечной точкой является единичный кватернион, slerp дает сегмент однопараметрической подгруппы как группы Ли трехмерных вращений, SO(3) , так и ее универсальной покрывающей группы единичных кватернионов, S ³. Слерп дает самый прямой и кратчайший путь между конечными точками кватернионов и отображает поворот на угол 2 Ом. Однако, поскольку покрытие двойное ( q и − q соответствуют одному и тому же вращению), путь вращения может повернуться либо «коротким путем» (менее 180 °), либо «длинным путем» (более 180 °). Длинных путей можно избежать, отрицая один конец, если скалярное произведение cos Ω отрицательно, таким образом гарантируя, что −90° ≤ Ω ≤ 90° .

У Слерпа также есть выражения в терминах алгебры кватернионов, все они используют возведение в степень . Действительные степени кватерниона определяются с помощью экспоненциальной функции кватерниона , записанной как e ^д и задается степенным рядом, одинаково знакомым из исчисления, комплексного анализа и матричной алгебры:

e^{q}=1+q+{\frac {q^{2}}{2}}+{\frac {q^{3}}{6}}+\cdots +{\frac {q^{n}}{n!}}+\cdots .

Записав единичный кватернион q в версора форме , cos Ω + v sin Ω , где v — единичный 3-вектор, и отметив, что квадрат кватерниона v ² равно −1 (что подразумевает кватернионную версию формулы Эйлера ), мы имеем e ^{v Ом} = q и q ^т знак равно потому что т Ω + v грех т Ω . Идентификация, представляющая интерес: q = q ₁ q ₀⁻¹, так что действительная часть q равна cos Ω , то же самое, что и геометрическое скалярное произведение, использованное выше. Вот четыре эквивалентных выражения кватернионов для slerp.

{\begin{aligned}\operatorname {slerp} (q_{0},q_{1},t)&=q_{0}(q_{0}^{-1}q_{1})^{t}\\[6pt]&=q_{1}(q_{1}^{-1}q_{0})^{1-t}\\[6pt]&=(q_{0}q_{1}^{-1})^{1-t}q_{1}\\[6pt]&=(q_{1}q_{0}^{-1})^{t}q_{0}\end{aligned}}

Производная , предполагая , slerp ( q ₀ , q ₁ ; t ) по t что концы фиксированы, равна log( q ₁ q ₀⁻¹) умноженное на значение функции, где натуральный логарифм кватерниона в данном случае дает половину трехмерного вектора угловой скорости . Начальный вектор касательной параллельно переносится к каждой касательной вдоль кривой; таким образом, кривая действительно является геодезической.

В касательном пространстве в любой точке кватернионной кривой обратная экспоненциальная карта преобразует кривую в отрезок прямой. Кривые Слерпа, не проходящие через точку, не могут преобразоваться в линии в касательном пространстве этой точки.

Кватернионные слерпы обычно используются для построения плавных кривых анимации путем имитации аффинных конструкций, таких как алгоритм де Кастельжо для кривых Безье . Поскольку сфера не является аффинным пространством , знакомые свойства аффинных конструкций могут оказаться неэффективными, хотя в остальном построенные кривые могут быть вполне удовлетворительными. Например, алгоритм де Кастельжо можно использовать для разделения кривой в аффинном пространстве; это не работает на сфере.

Двузначный slerp можно расширить для интерполяции среди множества единичных кватернионов, ^[2] но расширение теряет фиксированное время выполнения алгоритма slerp.

См. также

Ссылки

^ «Кен Шумейк — Дом» .
^ Пеннек, Ксавье (март 1998 г.). Вычисление среднего значения геометрических характеристик применительно к среднему вращению (отчет). ИНРИА . Проверено 19 июня 2020 г.

Внешние ссылки

Шумейк, Кен. «Анимация вращения с помощью кватернионных кривых» (PDF) . СИГРАФ 1985.
Эрик Б., Плотина; Мартин, Кох; Лиллхольм, Мартин (17 июля 1998 г.). «Кватернионы, интерполяция и анимация» (PDF) . Университет Копенгагена. Архивировано (PDF) из оригинала 30 августа 2017 г.
Блоу, Джонатан (26 февраля 2004 г.). «Понимание Slerp, а затем не использование его» . Архивировано из оригинала 25 августа 2017 г.
Мартин, Брайан (23 июня 1999 г.). «Брайан Мартин о Quaternion Animation» . Архивировано из оригинала 24 марта 2016 г.

[1] «Кен Шумейк — Дом» .

[2] Пеннек, Ксавье (март 1998 г.). Вычисление среднего значения геометрических характеристик применительно к среднему вращению (отчет). ИНРИА . Проверено 19 июня 2020 г.

[1]

[2]