Частота среза

Передаточная функция амплитуды полосового фильтра с нижней частотой среза 3 дБ f ₁ и верхней частотой среза 3 дБ f ₂

График Боде (логарифмический график частотной характеристики ) любого фильтра нижних частот первого порядка с нормированной частотой среза при $\omega$=1 и полоса пропускания с единичным усилением (0 дБ).

В физике и электротехнике частота среза , угловая частота или частота сбоя системы, — это граница частотной характеристики при которой энергия, проходящая через систему, начинает уменьшаться ( ослабляться или отражаться), а не проходить через нее.

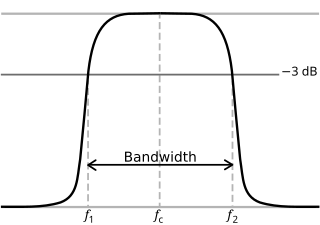
Обычно в электронных системах, таких как фильтры и каналы связи , частота среза применяется к краю характеристики нижних , верхних , полосовых или полосно-заграждающих характеристик – частота, характеризующая границу между полосой пропускания и полосой задерживания . Иногда это считается точкой в ​​отклике фильтра, где пересекаются полоса перехода и полоса пропускания, например, как это определяется точкой половинной мощности (частота, для которой выходной сигнал схемы составляет примерно -3,01 дБ от номинальной полосы пропускания). ценить). Альтернативно, угловая частота полосы задерживания может быть задана как точка, где встречаются переходная полоса и полоса задерживания: частота, для которой затухание больше, чем требуемое затухание в полосе задерживания, которое, например, может составлять 30 дБ или 100 дБ.

В случае волновода или антенны граничные частоты соответствуют нижней и верхней граничным длинам волн .

Электроника

В электронике частота среза или угловая частота — это частота , выше или ниже которой выходная мощность схемы , такой как линия , усилитель или электронный фильтр, упала до заданной пропорции мощности в полосе пропускания . Чаще всего эта пропорция составляет половину мощности полосы пропускания, также называемую точкой 3 дБ , поскольку падение на 3 дБ соответствует примерно половине мощности. Что касается коэффициента напряжения, то это падение до ${\textstyle {\sqrt {1/2}}\ \approx \ 0.707}$ напряжения полосы пропускания. Другие соотношения, помимо точки 3 дБ, также могут иметь значение, например, см. § Фильтры Чебышева ниже. Вдали от частоты среза в полосе перехода скорость нарастания затухания ( спада ) с логарифмом частоты асимптотически равна константе. Для сети первого порядка спад составляет -20 дБ на декаду (приблизительно -6 дБ на октаву ).

Пример однополюсной передаточной функции

Передаточная функция для простейшего фильтра нижних частот , $$H(s)={\frac {1}{1+\alpha s}},$$имеет единственный полюс в точке s = −1/ α . Величина этой функции в плоскости j' ω равна $$\left|H(j\omega )\right|=\left|{\frac {1}{1+\alpha j\omega }}\right|={\sqrt {\frac {1}{1+\alpha ^{2}\omega ^{2}}}}.$$

На отсечке $$\left|H(j\omega _{\mathrm {c} })\right|={\frac {1}{\sqrt {2}}}={\sqrt {\frac {1}{1+\alpha ^{2}\omega _{\mathrm {c} }^{2}}}}.$$

Следовательно, частота среза определяется выражением $$\omega _{\mathrm {c} }={\frac {1}{\alpha }}.$$

Где s — переменная s-плоскости , ω — угловая частота , а j — мнимая единица измерения .

Фильтры Чебышева

Иногда другие соотношения более удобны, чем точка 3 дБ. Например, в случае фильтра Чебышева частоту среза обычно определяют как точку после последнего пика частотной характеристики, в которой уровень упал до расчетного значения неравномерности полосы пропускания. Величина пульсаций в этом классе фильтров может быть установлена ​​разработчиком на любое желаемое значение, следовательно, используемый коэффициент может быть любым значением.

Радиосвязь

В радиосвязи радиоволны небесная связь представляет собой метод, при котором передаются под углом в небо и отражаются обратно на Землю слоями заряженных частиц в ионосфере . В этом контексте термин «частота среза» относится к максимальной полезной частоте , частоте, выше которой радиоволна не может отражаться от ионосферы под углом падения, необходимым для передачи между двумя указанными точками за счет отражения от слоя.

Волноводы

Частота среза электромагнитного волновода — это наименьшая частота, при которой в нем распространяется мода. В волоконной оптике чаще всего рассматривают длину волны отсечки — максимальную длину волны , которая будет распространяться в оптическом волокне или волноводе . Частота среза находится с помощью характеристического уравнения уравнения Гельмгольца для электромагнитных волн, которое получается из уравнения электромагнитных волн путем установки продольного волнового числа равным нулю и определения частоты. Таким образом, любая возбуждающая частота ниже частоты среза будет затухать, а не распространяться. Следующий вывод предполагает стены без потерь. Значение c, скорость света , следует принять за групповую скорость света в любом материале, заполняющем волновод.

Для прямоугольного волновода частота среза равна $$\omega _{c}=c{\sqrt {\left({\frac {m\pi }{a}}\right)^{2}+\left({\frac {n\pi }{b}}\right)^{2}}},$$где $m,n\geq 0$ — номера мод для сторон прямоугольника длиной $a$ и $b$ соответственно. Для режимов TE: $m,n\geq 0$ (но $m=n=0$ не допускается), а для режимов ТМ $m,n\geq 1$.

Частота среза моды TM ₀₁ (следующая по величине после доминирующей моды TE ₁₁ ) в волноводе круглого сечения (поперечно-магнитная мода без угловой зависимости и с наименьшей радиальной зависимостью) определяется выражением $$\omega _{c}=c{\frac {\chi _{01}}{r}}=c{\frac {2.4048}{r}},$$где $r$ - радиус волновода, а $\chi _{01}$ является первым корнем $J_{0}(r)$, функция Бесселя первого рода порядка 1.

Частота среза доминирующей моды TE ₁₁ определяется выражением $$\omega _{c}=c{\frac {\chi _{11}}{r}}=c{\frac {1.8412}{r}}$$

Однако частоту среза доминирующей моды можно уменьшить, установив перегородку внутри волновода круглого сечения. Для одномодового оптического волокна длина волны среза — это длина волны, при которой нормированная частота примерно равна 2,405.

Математический анализ

Отправной точкой является волновое уравнение (которое получено из уравнений Максвелла ), $$\left(\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial {t}^{2}}}\right)\psi (\mathbf {r} ,t)=0,$$которое становится уравнением Гельмгольца, если рассматривать только функции вида $$\psi (x,y,z,t)=\psi (x,y,z)e^{i\omega t}.$$Замена и оценка производной по времени дает $$\left(\nabla ^{2}+{\frac {\omega ^{2}}{c^{2}}}\right)\psi (x,y,z)=0.$$Функция $\psi$ здесь имеется в виду любое поле (электрическое поле или магнитное поле), не имеющее векторной составляющей в продольном направлении – «поперечное» поле. Свойством всех собственных мод электромагнитного волновода является то, что по крайней мере одно из двух полей является поперечным. Ось z определяется как направленная вдоль оси волновода.

«Продольную» производную в лапласиане можно дополнительно уменьшить, рассматривая только функции вида $$\psi (x,y,z,t)=\psi (x,y)e^{i\left(\omega t-k_{z}z\right)},$$где $k_{z}$ продольное волновое число , в результате чего $$\left(\nabla _{T}^{2}-k_{z}^{2}+{\frac {\omega ^{2}}{c^{2}}}\right)\psi (x,y,z)=0,$$где индекс T указывает на двумерный поперечный лапласиан. Последний шаг зависит от геометрии волновода. Проще всего решить геометрию прямоугольного волновода. В этом случае остаток лапласиана можно вычислить до его характеристического уравнения, рассматривая решения вида $$\psi (x,y,z,t)=\psi _{0}e^{i\left(\omega t-k_{z}z-k_{x}x-k_{y}y\right)}.$$Таким образом, для прямоугольной направляющей вычисляется лапласиан и приходим к $${\frac {\omega ^{2}}{c^{2}}}=k_{x}^{2}+k_{y}^{2}+k_{z}^{2}$$Поперечные волновые числа можно определить из граничных условий стоячей волны для поперечного сечения прямоугольной формы с размерами a и b : $$k_{x}={\frac {n\pi }{a}},$$$$k_{y}={\frac {m\pi }{b}},$$где n и m — два целых числа, представляющие конкретную собственную моду. Произведя окончательную замену, получим $${\frac {\omega ^{2}}{c^{2}}}=\left({\frac {n\pi }{a}}\right)^{2}+\left({\frac {m\pi }{b}}\right)^{2}+k_{z}^{2},$$что представляет собой закон дисперсии в прямоугольном волноводе. Частота среза $\omega _{c}$ - критическая частота между распространением и затуханием, которая соответствует частоте, на которой продольное волновое число $k_{z}$ равен нулю. Это дано $$\omega _{c}=c{\sqrt {\left({\frac {n\pi }{a}}\right)^{2}+\left({\frac {m\pi }{b}}\right)^{2}}}$$Волновые уравнения справедливы и ниже частоты среза, где продольное волновое число является мнимым. В этом случае поле экспоненциально затухает вдоль оси волновода, и волна, таким образом, затухает .

См. также

• Полная ширина на половине максимума
• Фильтр верхних частот
• Эффект Миллера
• Пространственная граничная частота (в оптических системах)
• Постоянная времени

Ссылки

• В этой статье использованы общедоступные материалы из Федеральный стандарт 1037C . Управление общего обслуживания . Архивировано из оригинала 22 января 2022 г. (в поддержку MIL-STD-188 ).

Внешние ссылки

• Расчет центральной частоты со средним геометрическим и сравнением со среднеарифметическим решением
• Преобразование частоты среза f _c и постоянной времени τ
• Математическое определение функций Бесселя и информация о них.