Вариационные байесовские методы

О методе приближения в квантовой механике см. Вариационный метод (квантовая механика) .

Вариационные байесовские методы — это семейство методов аппроксимации трудноразрешимых интегралов, возникающих при байесовском выводе и машинном обучении . Они обычно используются в сложных статистических моделях, состоящих из наблюдаемых переменных (обычно называемых «данными»), а также неизвестных параметров и скрытых переменных , с различными видами отношений между тремя типами случайных величин , которые могут быть описаны графической моделью . Как это типично для байесовского вывода, параметры и скрытые переменные группируются вместе как «ненаблюдаемые переменные». Вариационные байесовские методы в основном используются для двух целей:

1. Обеспечить аналитическую аппроксимацию апостериорной вероятности ненаблюдаемых переменных, чтобы сделать статистические выводы по этим переменным.
2. Получить нижнюю границу ( предельной вероятности иногда называемой доказательством ) наблюдаемых данных (т. е. предельной вероятности данных с учетом модели с маргинализацией, выполняемой по ненаблюдаемым переменным). Обычно это используется для выбора модели , общая идея заключается в том, что более высокая предельная вероятность для данной модели указывает на лучшее соответствие данных этой моделью и, следовательно, большую вероятность того, что рассматриваемая модель была той, которая сгенерировала данные. (См. также статью о байесовском факторе .)

В первой цели (аппроксимация апостериорной вероятности) вариационный Байес является альтернативой методам выборки Монте-Карло , в частности, методам Монте-Карло с цепью Маркова , таким как выборка Гиббса , для использования полностью байесовского подхода к статистическому выводу по сложным распределениям , которые трудно оценить напрямую или по образцу . В частности, в то время как методы Монте-Карло обеспечивают численную аппроксимацию точной апостериорной функции с использованием набора выборок, вариационный Байес обеспечивает локально оптимальное, точное аналитическое решение для аппроксимации апостериорной функции.

Вариационный Байес можно рассматривать как расширение алгоритма ожидания-максимизации (EM) от максимальной апостериорной оценки (оценка MAP) единственного наиболее вероятного значения каждого параметра до полностью байесовской оценки, которая вычисляет (приближение) всего апостериорного распределения. параметров и скрытых переменных. Как и в EM, он находит набор оптимальных значений параметров и имеет ту же переменную структуру, что и EM, основанную на наборе взаимосвязанных (взаимозависимых) уравнений, которые не могут быть решены аналитически.

Для многих приложений вариационный Байес дает решения, сравнимые по точности с выборкой Гиббса, но с большей скоростью. Однако получение набора уравнений, используемых для итеративного обновления параметров, часто требует большого объема работы по сравнению с получением сопоставимых уравнений выборки Гиббса. Это справедливо даже для многих моделей, которые концептуально довольно просты, как показано ниже в случае базовой неиерархической модели только с двумя параметрами и без скрытых переменных.

Математический вывод

Проблема

В вариационном выводе апостериорное распределение по набору ненаблюдаемых переменных $\mathbf {Z} =\{Z_{1}\dots Z_{n}\}$ учитывая некоторые данные $\mathbf {X}$ аппроксимируется так называемым вариационным распределением , $Q(\mathbf {Z} ):$

$P(\mathbf {Z} \mid \mathbf {X} )\approx Q(\mathbf {Z} ).$

Распределение $Q(\mathbf {Z} )$ ограничивается принадлежностью к семейству распределений более простой формы, чем $P(\mathbf {Z} \mid \mathbf {X} )$ (например, семейство гауссовских распределений), выбранное с намерением сделать $Q(\mathbf {Z} )$ аналогичен истинному заднему, $P(\mathbf {Z} \mid \mathbf {X} )$.

Сходство (или несходство) измеряется с помощью функции несходства. $d(Q;P)$ и, следовательно, вывод выполняется путем выбора распределения $Q(\mathbf {Z} )$ что сводит к минимуму $d(Q;P)$.

Дивергенция КЛ

Наиболее распространенный тип вариационного Байеса использует расхождение Кульбака – Лейблера (KL-дивергенцию) Q от P в качестве функции несходства. Этот выбор делает эту минимизацию осуществимой. KL-дивергенция определяется как

$D_{\mathrm {KL} }(Q\parallel P)\triangleq \sum _{\mathbf {Z} }Q(\mathbf {Z} )\log {\frac {Q(\mathbf {Z} )}{P(\mathbf {Z} \mid \mathbf {X} )}}.$

Обратите внимание, что Q и P перевернуты, чего можно было ожидать. Такое использование обратной КЛ-дивергенции концептуально похоже на алгоритм ожидания-максимизации . (Другое использование KL-дивергенции приводит к алгоритму распространения ожиданий .)

несговорчивость

Вариационные методы обычно используются для формирования аппроксимации:

$P(\mathbf {Z} \mid \mathbf {X} )={\frac {P(\mathbf {X} \mid \mathbf {Z} )P(\mathbf {Z} )}{P(\mathbf {X} )}}={\frac {P(\mathbf {X} \mid \mathbf {Z} )P(\mathbf {Z} )}{\int _{\mathbf {Z} }P(\mathbf {X} ,\mathbf {Z} ')\,d\mathbf {Z} '}}$

Маргинализация закончилась $\mathbf {Z}$ рассчитать $P(\mathbf {X} )$ в знаменателе обычно трудноразрешима, потому что, например, пространство поиска $\mathbf {Z}$ является комбинаторно большим. Поэтому мы ищем приближение, используя $Q(\mathbf {Z} )\approx P(\mathbf {Z} \mid \mathbf {X} )$.

Нижняя граница доказательств

Основная статья: Нижняя граница доказательств

При условии $P(\mathbf {Z} \mid \mathbf {X} )={\frac {P(\mathbf {X} ,\mathbf {Z} )}{P(\mathbf {X} )}}$, KL-дивергенция, указанная выше, также может быть записана как

$D_{\mathrm {KL} }(Q\parallel P)=\sum _{\mathbf {Z} }Q(\mathbf {Z} )\left[\log {\frac {Q(\mathbf {Z} )}{P(\mathbf {Z} ,\mathbf {X} )}}+\log P(\mathbf {X} )\right]=\sum _{\mathbf {Z} }Q(\mathbf {Z} )\left[\log Q(\mathbf {Z} )-\log P(\mathbf {Z} ,\mathbf {X} )\right]+\sum _{\mathbf {Z} }Q(\mathbf {Z} )\left[\log P(\mathbf {X} )\right]$

Потому что $P(\mathbf {X} )$ является константой по отношению к $\mathbf {Z}$ и $\sum _{\mathbf {Z} }Q(\mathbf {Z} )=1$ потому что $Q(\mathbf {Z} )$ это дистрибутив, у нас есть

$D_{\mathrm {KL} }(Q\parallel P)=\sum _{\mathbf {Z} }Q(\mathbf {Z} )\left[\log Q(\mathbf {Z} )-\log P(\mathbf {Z} ,\mathbf {X} )\right]+\log P(\mathbf {X} )$

которое согласно определению ожидаемого значения (для дискретной случайной величины ) можно записать следующим образом

$D_{\mathrm {KL} }(Q\parallel P)=\mathbb {E} _{\mathbf {Q} }\left[\log Q(\mathbf {Z} )-\log P(\mathbf {Z} ,\mathbf {X} )\right]+\log P(\mathbf {X} )$

который можно переставить так, чтобы он стал

$\log P(\mathbf {X} )=D_{\mathrm {KL} }(Q\parallel P)-\mathbb {E} _{\mathbf {Q} }\left[\log Q(\mathbf {Z} )-\log P(\mathbf {Z} ,\mathbf {X} )\right]=D_{\mathrm {KL} }(Q\parallel P)+{\mathcal {L}}(Q)$

Как журнал- свидетельство $\log P(\mathbf {X} )$ фиксируется относительно $Q$, максимизируя последний член ${\mathcal {L}}(Q)$ минимизирует расхождение KL $Q$ от $P$. При соответствующем выборе $Q$, ${\mathcal {L}}(Q)$ становится доступным для вычислений и максимизации. Следовательно, мы имеем как аналитическое приближение $Q$ для задней части $P(\mathbf {Z} \mid \mathbf {X} )$и нижняя граница ${\mathcal {L}}(Q)$ для протокола-доказательства $\log P(\mathbf {X} )$ (поскольку KL-дивергенция неотрицательна).

Нижняя граница ${\mathcal {L}}(Q)$ известна как (отрицательная) вариационная свободная энергия по аналогии с термодинамической свободной энергией , поскольку ее также можно выразить как отрицательную энергию. $\operatorname {E} _{Q}[\log P(\mathbf {Z} ,\mathbf {X} )]$ плюс энтропия ​ $Q$. Термин ${\mathcal {L}}(Q)$ также известен как Нижняя граница доказательств , сокращенно ELBO , чтобы подчеркнуть, что это нижняя граница (наихудший случай) логарифмической достоверности данных.

Доказательства

С помощью обобщенной теоремы Пифагора о дивергенции Брегмана , частным случаем которой является KL-дивергенция, можно показать, что:

Обобщенная теорема Пифагора для расхождения Брегмана

$D_{\mathrm {KL} }(Q\parallel P)\geq D_{\mathrm {KL} }(Q\parallel Q^{*})+D_{\mathrm {KL} }(Q^{*}\parallel P),\forall Q^{*}\in {\mathcal {C}}$

где ${\mathcal {C}}$ является выпуклым множеством и равенство имеет место, если:

$Q=Q^{*}\triangleq \arg \min _{Q\in {\mathcal {C}}}D_{\mathrm {KL} }(Q\parallel P).$

В этом случае глобальный минимизатор $Q^{*}(\mathbf {Z} )=q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})q^{*}(\mathbf {Z} _{2})=q^{*}(\mathbf {Z} _{2}\mid \mathbf {Z} _{1})q^{*}(\mathbf {Z} _{1}),$ с $\mathbf {Z} =\{\mathbf {Z_{1}} ,\mathbf {Z_{2}} \},$ можно найти следующим образом:

$q^{*}(\mathbf {Z} _{2})={\frac {P(\mathbf {X} )}{\zeta (\mathbf {X} )}}{\frac {P(\mathbf {Z} _{2}\mid \mathbf {X} )}{\exp(D_{\mathrm {KL} }(q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})\parallel P(\mathbf {Z} _{1}\mid \mathbf {Z} _{2},\mathbf {X} )))}}={\frac {1}{\zeta (\mathbf {X} )}}\exp \mathbb {E} _{q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})}\left(\log {\frac {P(\mathbf {Z} ,\mathbf {X} )}{q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})}}\right),$

в котором нормировочная константа равна:

$\zeta (\mathbf {X} )=P(\mathbf {X} )\int _{\mathbf {Z} _{2}}{\frac {P(\mathbf {Z} _{2}\mid \mathbf {X} )}{\exp(D_{\mathrm {KL} }(q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})\parallel P(\mathbf {Z} _{1}\mid \mathbf {Z} _{2},\mathbf {X} )))}}=\int _{\mathbf {Z} _{2}}\exp \mathbb {E} _{q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})}\left(\log {\frac {P(\mathbf {Z} ,\mathbf {X} )}{q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})}}\right).$

Термин $\zeta (\mathbf {X} )$ на практике часто называют нижней границей доказательств ( ELBO ), поскольку $P(\mathbf {X} )\geq \zeta (\mathbf {X} )=\exp({\mathcal {L}}(Q^{*}))$, как показано выше.

Поменявшись ролями $\mathbf {Z} _{1}$ и $\mathbf {Z} _{2},$ мы можем итеративно вычислить приближенное $q^{*}(\mathbf {Z} _{1})$ и $q^{*}(\mathbf {Z} _{2})$ маргинальных значений истинной модели $P(\mathbf {Z} _{1}\mid \mathbf {X} )$ и $P(\mathbf {Z} _{2}\mid \mathbf {X} ),$ соответственно. Хотя эта итерационная схема гарантированно сходится монотонно, конвергентный $Q^{*}$ является лишь локальным минимизатором $D_{\mathrm {KL} }(Q\parallel P)$.

Если ограниченное пространство ${\mathcal {C}}$ заключен в независимое пространство, т.е. $q^{*}(\mathbf {Z} _{1}\mid \mathbf {Z} _{2})=q^{*}(\mathbf {Z_{1}} ),$приведенная выше итерационная схема станет так называемым приближением среднего поля $Q^{*}(\mathbf {Z} )=q^{*}(\mathbf {Z} _{1})q^{*}(\mathbf {Z} _{2}),$как показано ниже.

Приближение среднего поля

Вариационное распределение $Q(\mathbf {Z} )$ обычно предполагается, что факторизуется по некоторому разделу скрытых переменных, т.е. по некоторому разделу скрытых переменных $\mathbf {Z}$ в $\mathbf {Z} _{1}\dots \mathbf {Z} _{M}$,

$Q(\mathbf {Z} )=\prod _{i=1}^{M}q_{i}(\mathbf {Z} _{i}\mid \mathbf {X} )$

можно показать, что «лучшее» распределение С помощью вариационного исчисления (отсюда и название «вариационный Байес») $q_{j}^{*}$ по каждому из факторов $q_{j}$ (с точки зрения распределения, минимизирующего KL-расхождение, как описано выше) удовлетворяет:

$q_{j}^{*}(\mathbf {Z} _{j}\mid \mathbf {X} )={\frac {e^{\operatorname {E} _{q_{-j}^{*}}[\ln p(\mathbf {Z} ,\mathbf {X} )]}}{\int e^{\operatorname {E} _{q_{-j}^{*}}[\ln p(\mathbf {Z} ,\mathbf {X} )]}\,d\mathbf {Z} _{j}}}$

где $\operatorname {E} _{q_{-j}^{*}}[\ln p(\mathbf {Z} ,\mathbf {X} )]$ - это математическое ожидание логарифма совместной вероятности данных и скрытых переменных, взятого относительно $q^{*}$ по всем переменным, не входящим в разбиение: см. лемму 4.1 из для вывода распределения $q_{j}^{*}(\mathbf {Z} _{j}\mid \mathbf {X} )$.

На практике мы обычно работаем с логарифмами, т.е.:

$\ln q_{j}^{*}(\mathbf {Z} _{j}\mid \mathbf {X} )=\operatorname {E} _{q_{-j}^{*}}[\ln p(\mathbf {Z} ,\mathbf {X} )]+{\text{constant}}$

Константа в приведенном выше выражении связана с константой нормализации (знаменатель в приведенном выше выражении для $q_{j}^{*}$) и обычно восстанавливается при проверке, поскольку остальную часть выражения обычно можно распознать как распределение известного типа (например, Гауссово , гамма и т. д.).

Используя свойства ожиданий, выражение $\operatorname {E} _{q_{-j}^{*}}[\ln p(\mathbf {Z} ,\mathbf {X} )]$ обычно можно упростить до функции фиксированных гиперпараметров предшествующих распределений по скрытым переменным и ожиданий (а иногда и более высоких моментов, таких как дисперсия ) скрытых переменных, не входящих в текущий раздел (т.е. скрытых переменных, не включенных в $\mathbf {Z} _{j}$). Это создает круговые зависимости между параметрами распределений переменных в одном разделе и ожиданиями переменных в других разделах. Это, естественно, предполагает итерационный алгоритм, очень похожий на EM ( алгоритм максимизации ожидания ), в котором ожидания (и, возможно, более высокие моменты) скрытых переменных инициализируются каким-то образом (возможно, случайным образом), а затем параметры каждого распределения вычисляется, в свою очередь, с использованием текущих значений ожиданий, после чего ожидание вновь вычисленного распределения устанавливается соответствующим образом в соответствии с вычисленными параметрами. Алгоритм такого типа гарантированно сходится .

Другими словами, для каждого из разбиений переменных, упростив выражение распределения по переменным разбиения и исследовав функциональную зависимость распределения от рассматриваемых переменных, обычно можно определить семейство распределения (что, в свою очередь, определяет значение константы). Формула для параметров распределения будет выражаться через гиперпараметры предыдущих распределений (которые являются известными константами), а также через ожидания функций переменных в других разделах. Обычно эти ожидания можно упростить до функций ожиданий самих переменных (т.е. средств ); иногда также появляются ожидания квадратов переменных (которые могут быть связаны с дисперсией переменных) или ожидания более высоких степеней (т.е. более высоких моментов ). В большинстве случаев распределения других переменных будут принадлежать к известным семействам, и можно найти формулы для соответствующих ожиданий. Однако эти формулы зависят от параметров этих распределений, которые, в свою очередь, зависят от ожиданий относительно других переменных. В результате формулы для параметров распределений каждой переменной могут быть выражены в виде серии уравнений с взаимными нелинейные зависимости между переменными. Обычно решить эту систему уравнений напрямую не представляется возможным. Однако, как описано выше, зависимости предполагают простой итерационный алгоритм, который в большинстве случаев гарантированно сходится. Пример сделает этот процесс более понятным.

Формула двойственности для вариационного вывода

Наглядная иллюстрация алгоритма вариационного вывода координат по формуле двойственности

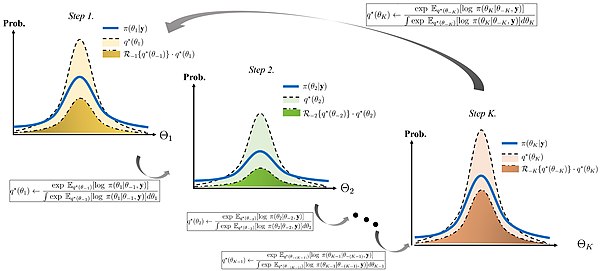
Следующая теорема называется формулой двойственности для вариационного вывода. Это объясняет некоторые важные свойства вариационных распределений, используемых в вариационных методах Байеса.

Теорема. Рассмотрим два вероятностных пространства. $(\Theta ,{\mathcal {F}},P)$ и $(\Theta ,{\mathcal {F}},Q)$ с $Q\ll P$. Предположим, что существует общая доминирующая вероятностная мера $\lambda$ такой, что $P\ll \lambda$ и $Q\ll \lambda$. Позволять $h$ обозначают любую действительную случайную величину на $(\Theta ,{\mathcal {F}},P)$ это удовлетворяет $h\in L_{1}(P)$. Тогда имеет место равенство

$\log E_{P}[\exp h]={\text{sup}}_{Q\ll P}\{E_{Q}[h]-D_{\text{KL}}(Q\parallel P)\}.$

Далее, верхняя грань в правой части достигается тогда и только тогда, когда выполняется

${\frac {q(\theta )}{p(\theta )}}={\frac {\exp h(\theta )}{E_{P}[\exp h]}},$

почти наверняка относительно вероятностной меры $Q$, где $p(\theta )=dP/d\lambda$ и $q(\theta )=dQ/d\lambda$ обозначим производные Радона–Никодима вероятностных мер $P$ и $Q$ относительно $\lambda$, соответственно.

Базовый пример

Рассмотрим простую неиерархическую байесовскую модель, состоящую из набора наблюдений iid из гауссовского распределения с неизвестными средним значением и дисперсией . Далее мы подробно рассмотрим эту модель, чтобы проиллюстрировать работу вариационного метода Байеса.

Для математического удобства в следующем примере мы работаем с точки зрения точности — то есть обратной величины дисперсии (или в многомерном гауссове, обратной ковариационной матрице ) — а не самой дисперсии. (С теоретической точки зрения точность и дисперсия эквивалентны, поскольку существует взаимно однозначное соответствие между ними .)

Математическая модель

Мы помещаем сопряженные априорные распределения в неизвестное среднее значение $\mu$ и точность $\tau$т.е. среднее значение также соответствует распределению Гаусса, а точность соответствует гамма-распределению . Другими словами:

${\begin{aligned}\tau &\sim \operatorname {Gamma} (a_{0},b_{0})\\\mu |\tau &\sim {\mathcal {N}}(\mu _{0},(\lambda _{0}\tau )^{-1})\\\{x_{1},\dots ,x_{N}\}&\sim {\mathcal {N}}(\mu ,\tau ^{-1})\\N&={\text{number of data points}}\end{aligned}}$

Гиперпараметры ​ $\mu _{0},\lambda _{0},a_{0}$ и $b_{0}$ в предыдущих распределениях фиксированы заданные значения. Им можно задать небольшие положительные числа, чтобы получить широкие априорные распределения, указывающие на незнание априорных распределений. $\mu$ и $\tau$.

Нам дано $N$ точки данных $\mathbf {X} =\{x_{1},\ldots ,x_{N}\}$ и наша цель — вывести апостериорное распределение $q(\mu ,\tau )=p(\mu ,\tau \mid x_{1},\ldots ,x_{N})$ параметров $\mu$ и $\tau .$

Совместная вероятность

Совместную вероятность всех переменных можно переписать как

$p(\mathbf {X} ,\mu ,\tau )=p(\mathbf {X} \mid \mu ,\tau )p(\mu \mid \tau )p(\tau )$

где отдельные факторы

${\begin{aligned}p(\mathbf {X} \mid \mu ,\tau )&=\prod _{n=1}^{N}{\mathcal {N}}(x_{n}\mid \mu ,\tau ^{-1})\\p(\mu \mid \tau )&={\mathcal {N}}\left(\mu \mid \mu _{0},(\lambda _{0}\tau )^{-1}\right)\\p(\tau )&=\operatorname {Gamma} (\tau \mid a_{0},b_{0})\end{aligned}}$

где

${\begin{aligned}{\mathcal {N}}(x\mid \mu ,\sigma ^{2})&={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{\frac {-(x-\mu )^{2}}{2\sigma ^{2}}}\\\operatorname {Gamma} (\tau \mid a,b)&={\frac {1}{\Gamma (a)}}b^{a}\tau ^{a-1}e^{-b\tau }\end{aligned}}$

Факторизованное приближение

Предположим, что $q(\mu ,\tau )=q(\mu )q(\tau )$, т. е. что апостериорное распределение разлагается на независимые факторы для $\mu$ и $\tau$. Этот тип предположения лежит в основе вариационного байесовского метода. Истинное апостериорное распределение на самом деле не учитывает этот фактор (на самом деле, в этом простом случае известно, что оно представляет собой гамма-распределение Гаусса ), и, следовательно, результат, который мы получим, будет аппроксимацией.

Вывод q ( µ )

Затем

${\begin{aligned}\ln q_{\mu }^{*}(\mu )&=\operatorname {E} _{\tau }\left[\ln p(\mathbf {X} \mid \mu ,\tau )+\ln p(\mu \mid \tau )+\ln p(\tau )\right]+C\\&=\operatorname {E} _{\tau }\left[\ln p(\mathbf {X} \mid \mu ,\tau )\right]+\operatorname {E} _{\tau }\left[\ln p(\mu \mid \tau )\right]+\operatorname {E} _{\tau }\left[\ln p(\tau )\right]+C\\&=\operatorname {E} _{\tau }\left[\ln \prod _{n=1}^{N}{\mathcal {N}}\left(x_{n}\mid \mu ,\tau ^{-1}\right)\right]+\operatorname {E} _{\tau }\left[\ln {\mathcal {N}}\left(\mu \mid \mu _{0},(\lambda _{0}\tau )^{-1}\right)\right]+C_{2}\\&=\operatorname {E} _{\tau }\left[\ln \prod _{n=1}^{N}{\sqrt {\frac {\tau }{2\pi }}}e^{-{\frac {(x_{n}-\mu )^{2}\tau }{2}}}\right]+\operatorname {E} _{\tau }\left[\ln {\sqrt {\frac {\lambda _{0}\tau }{2\pi }}}e^{-{\frac {(\mu -\mu _{0})^{2}\lambda _{0}\tau }{2}}}\right]+C_{2}\\&=\operatorname {E} _{\tau }\left[\sum _{n=1}^{N}\left({\frac {1}{2}}(\ln \tau -\ln 2\pi )-{\frac {(x_{n}-\mu )^{2}\tau }{2}}\right)\right]+\operatorname {E} _{\tau }\left[{\frac {1}{2}}(\ln \lambda _{0}+\ln \tau -\ln 2\pi )-{\frac {(\mu -\mu _{0})^{2}\lambda _{0}\tau }{2}}\right]+C_{2}\\&=\operatorname {E} _{\tau }\left[\sum _{n=1}^{N}-{\frac {(x_{n}-\mu )^{2}\tau }{2}}\right]+\operatorname {E} _{\tau }\left[-{\frac {(\mu -\mu _{0})^{2}\lambda _{0}\tau }{2}}\right]+\operatorname {E} _{\tau }\left[\sum _{n=1}^{N}{\frac {1}{2}}(\ln \tau -\ln 2\pi )\right]+\operatorname {E} _{\tau }\left[{\frac {1}{2}}(\ln \lambda _{0}+\ln \tau -\ln 2\pi )\right]+C_{2}\\&=\operatorname {E} _{\tau }\left[\sum _{n=1}^{N}-{\frac {(x_{n}-\mu )^{2}\tau }{2}}\right]+\operatorname {E} _{\tau }\left[-{\frac {(\mu -\mu _{0})^{2}\lambda _{0}\tau }{2}}\right]+C_{3}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{\sum _{n=1}^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _{0})^{2}\right\}+C_{3}\end{aligned}}$

В приведенном выше выводе $C$, $C_{2}$ и $C_{3}$ относятся к значениям, которые постоянны по отношению к $\mu$. Обратите внимание, что термин $\operatorname {E} _{\tau }[\ln p(\tau )]$ не является функцией $\mu$ и будет иметь одно и то же значение независимо от значения $\mu$. Следовательно, в строке 3 мы можем объединить его с постоянным членом в конце. То же самое делаем в строке 7.

Последняя строка представляет собой просто квадратичный полином от $\mu$. Так как это логарифм $q_{\mu }^{*}(\mu )$, мы можем это видеть $q_{\mu }^{*}(\mu )$ само по себе является распределением Гаусса .

С помощью определенного количества утомительных математических вычислений (расширение квадратов внутри фигурных скобок, выделение и группировка терминов, включающих $\mu$ и $\mu ^{2}$ и квадрат завершаем $\mu$), мы можем вывести параметры распределения Гаусса:

${\begin{aligned}\ln q_{\mu }^{*}(\mu )&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{\sum _{n=1}^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _{0})^{2}\right\}+C_{3}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{\sum _{n=1}^{N}(x_{n}^{2}-2x_{n}\mu +\mu ^{2})+\lambda _{0}(\mu ^{2}-2\mu _{0}\mu +\mu _{0}^{2})\right\}+C_{3}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{\left(\sum _{n=1}^{N}x_{n}^{2}\right)-2\left(\sum _{n=1}^{N}x_{n}\right)\mu +\left(\sum _{n=1}^{N}\mu ^{2}\right)+\lambda _{0}\mu ^{2}-2\lambda _{0}\mu _{0}\mu +\lambda _{0}\mu _{0}^{2}\right\}+C_{3}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{(\lambda _{0}+N)\mu ^{2}-2\left(\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}\right)\mu +\left(\sum _{n=1}^{N}x_{n}^{2}\right)+\lambda _{0}\mu _{0}^{2}\right\}+C_{3}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{(\lambda _{0}+N)\mu ^{2}-2\left(\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}\right)\mu \right\}+C_{4}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{(\lambda _{0}+N)\mu ^{2}-2\left({\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)(\lambda _{0}+N)\mu \right\}+C_{4}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{(\lambda _{0}+N)\left(\mu ^{2}-2\left({\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)\mu \right)\right\}+C_{4}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{(\lambda _{0}+N)\left(\mu ^{2}-2\left({\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)\mu +\left({\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)^{2}-\left({\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)^{2}\right)\right\}+C_{4}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{(\lambda _{0}+N)\left(\mu ^{2}-2\left({\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)\mu +\left({\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)^{2}\right)\right\}+C_{5}\\&=-{\frac {\operatorname {E} _{\tau }[\tau ]}{2}}\left\{(\lambda _{0}+N)\left(\mu -{\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)^{2}\right\}+C_{5}\\&=-{\frac {1}{2}}(\lambda _{0}+N)\operatorname {E} _{\tau }[\tau ]\left(\mu -{\frac {\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}}{\lambda _{0}+N}}\right)^{2}+C_{5}\end{aligned}}$

Обратите внимание, что все вышеперечисленные шаги можно сократить, используя формулу суммы двух квадратичных дробей .

Другими словами:

${\begin{aligned}q_{\mu }^{*}(\mu )&\sim {\mathcal {N}}(\mu \mid \mu _{N},\lambda _{N}^{-1})\\\mu _{N}&={\frac {\lambda _{0}\mu _{0}+N{\bar {x}}}{\lambda _{0}+N}}\\\lambda _{N}&=(\lambda _{0}+N)\operatorname {E} _{\tau }[\tau ]\\{\bar {x}}&={\frac {1}{N}}\sum _{n=1}^{N}x_{n}\end{aligned}}$

Вывод q(τ)

Вывод $q_{\tau }^{*}(\tau )$ аналогично предыдущему, хотя для краткости мы опускаем некоторые детали.

${\begin{aligned}\ln q_{\tau }^{*}(\tau )&=\operatorname {E} _{\mu }[\ln p(\mathbf {X} \mid \mu ,\tau )+\ln p(\mu \mid \tau )]+\ln p(\tau )+{\text{constant}}\\&=(a_{0}-1)\ln \tau -b_{0}\tau +{\frac {1}{2}}\ln \tau +{\frac {N}{2}}\ln \tau -{\frac {\tau }{2}}\operatorname {E} _{\mu }\left[\sum _{n=1}^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _{0})^{2}\right]+{\text{constant}}\end{aligned}}$

Возведя в степень обе стороны, мы увидим, что $q_{\tau }^{*}(\tau )$ представляет собой гамма-распределение . Конкретно:

${\begin{aligned}q_{\tau }^{*}(\tau )&\sim \operatorname {Gamma} (\tau \mid a_{N},b_{N})\\a_{N}&=a_{0}+{\frac {N+1}{2}}\\b_{N}&=b_{0}+{\frac {1}{2}}\operatorname {E} _{\mu }\left[\sum _{n=1}^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _{0})^{2}\right]\end{aligned}}$

Алгоритм расчета параметров

Подведем итоги предыдущих разделов:

${\begin{aligned}q_{\mu }^{*}(\mu )&\sim {\mathcal {N}}(\mu \mid \mu _{N},\lambda _{N}^{-1})\\\mu _{N}&={\frac {\lambda _{0}\mu _{0}+N{\bar {x}}}{\lambda _{0}+N}}\\\lambda _{N}&=(\lambda _{0}+N)\operatorname {E} _{\tau }[\tau ]\\{\bar {x}}&={\frac {1}{N}}\sum _{n=1}^{N}x_{n}\end{aligned}}$

и

${\begin{aligned}q_{\tau }^{*}(\tau )&\sim \operatorname {Gamma} (\tau \mid a_{N},b_{N})\\a_{N}&=a_{0}+{\frac {N+1}{2}}\\b_{N}&=b_{0}+{\frac {1}{2}}\operatorname {E} _{\mu }\left[\sum _{n=1}^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _{0})^{2}\right]\end{aligned}}$

В каждом случае параметры распределения по одной из переменных зависят от ожиданий, принятых по отношению к другой переменной. Мы можем расширить ожидания, используя стандартные формулы для математических ожиданий моментов гауссовского и гамма-распределений:

${\begin{aligned}\operatorname {E} [\tau \mid a_{N},b_{N}]&={\frac {a_{N}}{b_{N}}}\\\operatorname {E} \left[\mu \mid \mu _{N},\lambda _{N}^{-1}\right]&=\mu _{N}\\\operatorname {E} \left[X^{2}\right]&=\operatorname {Var} (X)+(\operatorname {E} [X])^{2}\\\operatorname {E} \left[\mu ^{2}\mid \mu _{N},\lambda _{N}^{-1}\right]&=\lambda _{N}^{-1}+\mu _{N}^{2}\end{aligned}}$

Применение этих формул к приведенным выше уравнениям в большинстве случаев тривиально, но уравнение для $b_{N}$ требует больше работы:

${\begin{aligned}b_{N}&=b_{0}+{\frac {1}{2}}\operatorname {E} _{\mu }\left[\sum _{n=1}^{N}(x_{n}-\mu )^{2}+\lambda _{0}(\mu -\mu _{0})^{2}\right]\\&=b_{0}+{\frac {1}{2}}\operatorname {E} _{\mu }\left[(\lambda _{0}+N)\mu ^{2}-2\left(\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}\right)\mu +\left(\sum _{n=1}^{N}x_{n}^{2}\right)+\lambda _{0}\mu _{0}^{2}\right]\\&=b_{0}+{\frac {1}{2}}\left[(\lambda _{0}+N)\operatorname {E} _{\mu }[\mu ^{2}]-2\left(\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}\right)\operatorname {E} _{\mu }[\mu ]+\left(\sum _{n=1}^{N}x_{n}^{2}\right)+\lambda _{0}\mu _{0}^{2}\right]\\&=b_{0}+{\frac {1}{2}}\left[(\lambda _{0}+N)\left(\lambda _{N}^{-1}+\mu _{N}^{2}\right)-2\left(\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}\right)\mu _{N}+\left(\sum _{n=1}^{N}x_{n}^{2}\right)+\lambda _{0}\mu _{0}^{2}\right]\\\end{aligned}}$

Затем мы можем записать уравнения параметров следующим образом, без каких-либо ожиданий:

${\begin{aligned}\mu _{N}&={\frac {\lambda _{0}\mu _{0}+N{\bar {x}}}{\lambda _{0}+N}}\\\lambda _{N}&=(\lambda _{0}+N){\frac {a_{N}}{b_{N}}}\\{\bar {x}}&={\frac {1}{N}}\sum _{n=1}^{N}x_{n}\\a_{N}&=a_{0}+{\frac {N+1}{2}}\\b_{N}&=b_{0}+{\frac {1}{2}}\left[(\lambda _{0}+N)\left(\lambda _{N}^{-1}+\mu _{N}^{2}\right)-2\left(\lambda _{0}\mu _{0}+\sum _{n=1}^{N}x_{n}\right)\mu _{N}+\left(\sum _{n=1}^{N}x_{n}^{2}\right)+\lambda _{0}\mu _{0}^{2}\right]\end{aligned}}$

Обратите внимание, что между формулами для $\lambda _{N}$и $b_{N}$. Это, естественно, предполагает EM -подобный алгоритм:

1. Вычислить $\sum _{n=1}^{N}x_{n}$ и $\sum _{n=1}^{N}x_{n}^{2}.$ Используйте эти значения для вычисления $\mu _{N}$ и $a_{N}.$
2. Инициализировать $\lambda _{N}$ до некоторого произвольного значения.
3. Используйте текущее значение $\lambda _{N},$ наряду с известными значениями других параметров, чтобы вычислить $b_{N}$.
4. Используйте текущее значение $b_{N},$ наряду с известными значениями других параметров, чтобы вычислить $\lambda _{N}$.
5. Повторяйте последние два шага до тех пор, пока не произойдет сходимость (т. е. пока ни одно из значений не изменится более чем на небольшую величину).

Затем у нас есть значения гиперпараметров аппроксимирующих распределений апостериорных параметров, которые мы можем использовать для вычисления любых желаемых свойств апостериорного показателя — например, его среднего значения и дисперсии, 95%-ной области с самой высокой плотностью (наименьший интервал, включающий 95 % от общей вероятности) и т. д.

Можно показать, что этот алгоритм гарантированно сходится к локальному максимуму.

Отметим также, что апостериорные распределения имеют ту же форму, что и соответствующие априорные распределения. Мы не этого предполагали; единственное предположение, которое мы сделали, заключалось в том, что распределения факторизуются, и форма распределений получается естественным образом. Оказывается (см. ниже), что тот факт, что апостериорные распределения имеют ту же форму, что и априорные распределения, является не совпадением, а общим результатом всякий раз, когда априорные распределения являются членами экспоненциального семейства , что имеет место для большинства стандартные дистрибутивы.

Дальнейшее обсуждение

Пошаговый рецепт

В приведенном выше примере показан метод, с помощью которого вариационно-байесовская аппроксимация апостериорной плотности вероятности в данной байесовской сети выводится :

1. Опишите сеть с помощью графической модели , определив наблюдаемые переменные (данные). $\mathbf {X}$ и ненаблюдаемые переменные ( параметры ${\boldsymbol {\Theta }}$ и скрытые переменные $\mathbf {Z}$) и их условные распределения вероятностей . Затем вариационный Байес построит аппроксимацию апостериорной вероятности. $p(\mathbf {Z} ,{\boldsymbol {\Theta }}\mid \mathbf {X} )$. Основное свойство аппроксимации состоит в том, что это факторизованное распределение, т.е. произведение двух или более независимых распределений по непересекающимся подмножествам ненаблюдаемых переменных.
2. Разделите ненаблюдаемые переменные на два или более подмножества, на основе которых будут получены независимые факторы. Для этого не существует универсальной процедуры; создание слишком большого количества подмножеств дает плохую аппроксимацию, а создание слишком малого количества делает всю вариационную процедуру Байеса неразрешимой. Обычно первое разделение заключается в разделении параметров и скрытых переменных; часто этого достаточно, чтобы получить приемлемый результат. Предположим, что разделы называются $\mathbf {Z} _{1},\ldots ,\mathbf {Z} _{M}$.
3. Для данного раздела $\mathbf {Z} _{j}$, запишите формулу наилучшего аппроксимирующего распределения $q_{j}^{*}(\mathbf {Z} _{j}\mid \mathbf {X} )$ используя основное уравнение $\ln q_{j}^{*}(\mathbf {Z} _{j}\mid \mathbf {X} )=\operatorname {E} _{i\neq j}[\ln p(\mathbf {Z} ,\mathbf {X} )]+{\text{constant}}$ .
4. Заполните формулу совместного распределения вероятностей, используя графическую модель. Любые условные распределения компонентов, которые не включают ни одну из переменных в $\mathbf {Z} _{j}$ можно игнорировать; они будут свернуты в постоянный член.
5. Упростите формулу и примените оператор ожидания, следуя приведенному выше примеру. В идеале это должно упроститься до ожиданий базовых функций переменных, не входящих в $\mathbf {Z} _{j}$ (например, первый или второй необработанные моменты , математическое ожидание логарифма и т. д.). Чтобы вариационная процедура Байеса работала хорошо, эти ожидания обычно должны быть выражены аналитически как функции параметров и/или гиперпараметров распределений этих переменных. Во всех случаях эти математические ожидания являются константами по отношению к переменным в текущем разделе.
6. Функциональная форма формулы относительно переменных текущего раздела указывает на тип распределения. В частности, возведение формулы в степень генерирует функцию плотности вероятности (PDF) распределения (или, по крайней мере, что-то пропорциональное ей с неизвестной константой нормализации ). Чтобы весь метод был управляемым, должна быть возможность распознать, что функциональная форма принадлежит известному распределению. Для преобразования формулы в форму, соответствующую PDF известного распределения, могут потребоваться значительные математические манипуляции. Когда это возможно, константа нормализации может быть восстановлена ​​по определению, а уравнения для параметров известного распределения могут быть получены путем извлечения соответствующих частей формулы.
7. Когда все ожидания могут быть аналитически заменены функциями переменных, не входящих в текущее разбиение, а PDF-файл представлен в форме, позволяющей идентифицировать его с известным распределением, результатом является набор уравнений, выражающих значения оптимальных параметров как функции параметры переменных в других разделах.
8. Когда эту процедуру можно применить ко всем разделам, результатом является набор взаимосвязанных уравнений, определяющих оптимальные значения всех параметров.
9. Затем применяется процедура типа ожидания-максимизации (EM), выбирающая начальное значение для каждого параметра и повторяющаяся серия шагов, где на каждом этапе мы циклически просматриваем уравнения, обновляя каждый параметр по очереди. Это гарантированно сходится.

Наиболее важные моменты

Из-за всех математических манипуляций легко потерять общую картину. Важные вещи:

1. Идея вариационного Байеса состоит в том, чтобы построить аналитическую аппроксимацию апостериорной вероятности набора ненаблюдаемых переменных (параметров и скрытых переменных) по данным. Это означает, что форма решения аналогична другим методам байесовского вывода , таким как выборка Гиббса — то есть распределение, которое стремится описать все, что известно о переменных. Как и в других байесовских методах – но в отличие, например, от методов максимизации ожидания (EM) или других методов максимального правдоподобия – оба типа ненаблюдаемых переменных (т.е. параметры и скрытые переменные) обрабатываются одинаково, т.е. как случайные величины . Оценки переменных затем можно получить стандартными байесовскими способами, например, вычислив среднее значение распределения для получения одноточечной оценки или выведя достоверный интервал , область с наибольшей плотностью и т. д.
2. «Аналитическая аппроксимация» означает, что можно записать формулу апостериорного распределения. Формула обычно состоит из произведения известных распределений вероятностей, каждое из которых факторизуется по набору ненаблюдаемых переменных (т.е. оно условно независимо от других переменных с учетом наблюдаемых данных). Эта формула не является истинным апостериорным распределением, а является его приближением; в частности, оно, как правило, довольно близко согласуется в самые низкие моменты ненаблюдаемых переменных, например среднего значения и дисперсии .
3. Результатом всех математических манипуляций является (1) идентичность распределений вероятностей, составляющих факторы, и (2) взаимозависимые формулы для параметров этих распределений. Фактические значения этих параметров вычисляются численно с помощью поочередной итерационной процедуры, очень похожей на EM.

По сравнению с ожиданием-максимизацией (EM)

Вариационный байесовский метод (ВБ) часто сравнивают с ожиданием-максимизацией (ЕМ). Реальная численная процедура очень похожа, поскольку обе они представляют собой чередующиеся итерационные процедуры, которые последовательно сходятся к оптимальным значениям параметров. Начальные шаги по получению соответствующих процедур также отчасти схожи: оба начинаются с формул для плотностей вероятности и оба включают значительное количество математических манипуляций.

Однако существует ряд различий. Самое главное — то, что вычисляется.

• EM вычисляет точечные оценки апостериорного распределения тех случайных величин, которые можно отнести к категории «параметров», но только оценки фактических апостериорных распределений скрытых переменных (по крайней мере, в «мягком EM», и часто только тогда, когда скрытые переменные дискретны). ). Вычисленные точечные оценки представляют собой моды этих параметров; никакой другой информации нет.
• VB, с другой стороны, вычисляет оценки фактического апостериорного распределения всех переменных, как параметров, так и скрытых переменных. Когда необходимо получить точечные оценки, обычно среднее значение используется , а не мода, как это обычно бывает в байесовском выводе. При этом параметры, рассчитанные в VB, не имеют того же значения, что и в EM. EM сама вычисляет оптимальные значения параметров сети Байеса. VB вычисляет оптимальные значения параметров распределений, используемых для аппроксимации параметров и скрытых переменных сети Байеса. Например, типичная модель гауссовой смеси будет иметь параметры для среднего значения и дисперсии каждого из компонентов смеси. ЭМ будет напрямую оценивать оптимальные значения этих параметров. Однако VB сначала подгонял бы распределение под эти параметры — обычно в форме априорного распределения , например, обратного гамма-распределения в нормальном масштабе — и затем вычислял бы значения параметров этого априорного распределения, т.е. гиперпараметры . В этом случае VB вычислит оптимальные оценки четырех параметров обратного гамма-распределения в нормальном масштабе, которое описывает совместное распределение среднего значения и дисперсии компонента.

Более сложный пример

Модель байесовской смеси Гаусса с использованием пластинчатых обозначений . Меньшие квадраты обозначают фиксированные параметры; большие кружки обозначают случайные величины. Заполненные фигуры обозначают известные значения. Индикация [K] означает вектор размера K ; [ D , D ] означает матрицу размера D × D ; K Только означает категориальную переменную с K результатами. Волнистая линия, идущая от z и заканчивающаяся перекладиной, указывает на переключатель — значение этой переменной выбирает для других входящих переменных, какое значение использовать из size- K . массива возможных значений

Представьте себе модель байесовской смеси Гаусса, описываемую следующим образом:

${\begin{aligned}\mathbf {\pi } &\sim \operatorname {SymDir} (K,\alpha _{0})\\\mathbf {\Lambda } _{i=1\dots K}&\sim {\mathcal {W}}(\mathbf {W} _{0},\nu _{0})\\\mathbf {\mu } _{i=1\dots K}&\sim {\mathcal {N}}(\mathbf {\mu } _{0},(\beta _{0}\mathbf {\Lambda } _{i})^{-1})\\\mathbf {z} [i=1\dots N]&\sim \operatorname {Mult} (1,\mathbf {\pi } )\\\mathbf {x} _{i=1\dots N}&\sim {\mathcal {N}}(\mathbf {\mu } _{z_{i}},{\mathbf {\Lambda } _{z_{i}}}^{-1})\\K&={\text{number of mixing components}}\\N&={\text{number of data points}}\end{aligned}}$

Примечание:

• SymDir() — симметричное распределение Дирихле размерности. $K$, с гиперпараметром для каждого компонента, установленным на $\alpha _{0}$. Распределение Дирихле является сопряженным априорным по отношению к категориальному распределению или полиномиальному распределению .
• ${\mathcal {W}}()$ — это распределение Уишарта , которое является сопряженным априором матрицы точности (обратной ковариационной матрицы ) для многомерного распределения Гаусса .
• Mult() — это полиномиальное распределение по одному наблюдению (эквивалентно категориальному распределению ). Пространство состояний представляет собой представление «один из K», т.е. $K$-мерный вектор, в котором один из элементов равен 1 (определяющий идентичность наблюдения), а все остальные элементы равны 0.
• ${\mathcal {N}}()$ - это распределение Гаусса , в данном случае именно многомерное распределение Гаусса .

Интерпретация вышеуказанных переменных следующая:

• $\mathbf {X} =\{\mathbf {x} _{1},\dots ,\mathbf {x} _{N}\}$ это набор $N$ точки данных, каждая из которых представляет собой $D$-мерный вектор, распределенный согласно многомерному распределению Гаусса .
• $\mathbf {Z} =\{\mathbf {z} _{1},\dots ,\mathbf {z} _{N}\}$ представляет собой набор скрытых переменных, по одной на каждую точку данных, определяющих, какому компоненту смеси принадлежит соответствующая точка данных, с использованием векторного представления «один из K» с компонентами $z_{nk}$ для $k=1\dots K$, как описано выше.
• $\mathbf {\pi }$ это пропорции смешивания $K$ компоненты смеси.
• $\mathbf {\mu } _{i=1\dots K}$ и $\mathbf {\Lambda } _{i=1\dots K}$ укажите параметры ( среднее значение и точность ), связанные с каждым компонентом смеси.

Совместную вероятность всех переменных можно переписать как

$p(\mathbf {X} ,\mathbf {Z} ,\mathbf {\pi } ,\mathbf {\mu } ,\mathbf {\Lambda } )=p(\mathbf {X} \mid \mathbf {Z} ,\mathbf {\mu } ,\mathbf {\Lambda } )p(\mathbf {Z} \mid \mathbf {\pi } )p(\mathbf {\pi } )p(\mathbf {\mu } \mid \mathbf {\Lambda } )p(\mathbf {\Lambda } )$

где отдельные факторы

${\begin{aligned}p(\mathbf {X} \mid \mathbf {Z} ,\mathbf {\mu } ,\mathbf {\Lambda } )&=\prod _{n=1}^{N}\prod _{k=1}^{K}{\mathcal {N}}(\mathbf {x} _{n}\mid \mathbf {\mu } _{k},\mathbf {\Lambda } _{k}^{-1})^{z_{nk}}\\p(\mathbf {Z} \mid \mathbf {\pi } )&=\prod _{n=1}^{N}\prod _{k=1}^{K}\pi _{k}^{z_{nk}}\\p(\mathbf {\pi } )&={\frac {\Gamma (K\alpha _{0})}{\Gamma (\alpha _{0})^{K}}}\prod _{k=1}^{K}\pi _{k}^{\alpha _{0}-1}\\p(\mathbf {\mu } \mid \mathbf {\Lambda } )&=\prod _{k=1}^{K}{\mathcal {N}}(\mathbf {\mu } _{k}\mid \mathbf {\mu } _{0},(\beta _{0}\mathbf {\Lambda } _{k})^{-1})\\p(\mathbf {\Lambda } )&=\prod _{k=1}^{K}{\mathcal {W}}(\mathbf {\Lambda } _{k}\mid \mathbf {W} _{0},\nu _{0})\end{aligned}}$

где

${\begin{aligned}{\mathcal {N}}(\mathbf {x} \mid \mathbf {\mu } ,\mathbf {\Sigma } )&={\frac {1}{(2\pi )^{D/2}}}{\frac {1}{|\mathbf {\Sigma } |^{1/2}}}\exp \left\{-{\frac {1}{2}}(\mathbf {x} -\mathbf {\mu } )^{\rm {T}}\mathbf {\Sigma } ^{-1}(\mathbf {x} -\mathbf {\mu } )\right\}\\{\mathcal {W}}(\mathbf {\Lambda } \mid \mathbf {W} ,\nu )&=B(\mathbf {W} ,\nu )|\mathbf {\Lambda } |^{(\nu -D-1)/2}\exp \left(-{\frac {1}{2}}\operatorname {Tr} (\mathbf {W} ^{-1}\mathbf {\Lambda } )\right)\\B(\mathbf {W} ,\nu )&=|\mathbf {W} |^{-\nu /2}\left\{2^{\nu D/2}\pi ^{D(D-1)/4}\prod _{i=1}^{D}\Gamma \left({\frac {\nu +1-i}{2}}\right)\right\}^{-1}\\D&={\text{dimensionality of each data point}}\end{aligned}}$

Предположим, что $q(\mathbf {Z} ,\mathbf {\pi } ,\mathbf {\mu } ,\mathbf {\Lambda } )=q(\mathbf {Z} )q(\mathbf {\pi } ,\mathbf {\mu } ,\mathbf {\Lambda } )$.

Затем

${\begin{aligned}\ln q^{*}(\mathbf {Z} )&=\operatorname {E} _{\mathbf {\pi } ,\mathbf {\mu } ,\mathbf {\Lambda } }[\ln p(\mathbf {X} ,\mathbf {Z} ,\mathbf {\pi } ,\mathbf {\mu } ,\mathbf {\Lambda } )]+{\text{constant}}\\&=\operatorname {E} _{\mathbf {\pi } }[\ln p(\mathbf {Z} \mid \mathbf {\pi } )]+\operatorname {E} _{\mathbf {\mu } ,\mathbf {\Lambda } }[\ln p(\mathbf {X} \mid \mathbf {Z} ,\mathbf {\mu } ,\mathbf {\Lambda } )]+{\text{constant}}\\&=\sum _{n=1}^{N}\sum _{k=1}^{K}z_{nk}\ln \rho _{nk}+{\text{constant}}\end{aligned}}$

где мы определили

$\ln \rho _{nk}=\operatorname {E} [\ln \pi _{k}]+{\frac {1}{2}}\operatorname {E} [\ln |\mathbf {\Lambda } _{k}|]-{\frac {D}{2}}\ln(2\pi )-{\frac {1}{2}}\operatorname {E} _{\mathbf {\mu } _{k},\mathbf {\Lambda } _{k}}[(\mathbf {x} _{n}-\mathbf {\mu } _{k})^{\rm {T}}\mathbf {\Lambda } _{k}(\mathbf {x} _{n}-\mathbf {\mu } _{k})]$

Возведение в степень обеих частей формулы для $\ln q^{*}(\mathbf {Z} )$ урожайность

$q^{*}(\mathbf {Z} )\propto \prod _{n=1}^{N}\prod _{k=1}^{K}\rho _{nk}^{z_{nk}}$

Требование, чтобы это было нормализовано, в конечном итоге требует, чтобы $\rho _{nk}$ суммировать до 1 по всем значениям $k$, уступая

$q^{*}(\mathbf {Z} )=\prod _{n=1}^{N}\prod _{k=1}^{K}r_{nk}^{z_{nk}}$

где

$r_{nk}={\frac {\rho _{nk}}{\sum _{j=1}^{K}\rho _{nj}}}$

Другими словами, $q^{*}(\mathbf {Z} )$ является продуктом полиномиальных распределений одного наблюдения и факторов по каждому отдельному наблюдению. $\mathbf {z} _{n}$, которое распространяется как полиномиальное распределение одного наблюдения с параметрами $r_{nk}$ для $k=1\dots K$.

Кроме того, отметим, что

$\operatorname {E} [z_{nk}]=r_{nk}\,$

что является стандартным результатом для категориальных распределений.

Теперь, учитывая фактор $q(\mathbf {\pi } ,\mathbf {\mu } ,\mathbf {\Lambda } )$, обратите внимание, что это автоматически учитывается $q(\mathbf {\pi } )\prod _{k=1}^{K}q(\mathbf {\mu } _{k},\mathbf {\Lambda } _{k})$ из-за структуры графической модели, определяющей нашу модель гауссовской смеси, указанной выше.

Затем,

${\begin{aligned}\ln q^{*}(\mathbf {\pi } )&=\ln p(\mathbf {\pi } )+\operatorname {E} _{\mathbf {Z} }[\ln p(\mathbf {Z} \mid \mathbf {\pi } )]+{\text{constant}}\\&=(\alpha _{0}-1)\sum _{k=1}^{K}\ln \pi _{k}+\sum _{n=1}^{N}\sum _{k=1}^{K}r_{nk}\ln \pi _{k}+{\text{constant}}\end{aligned}}$

Взяв экспоненту обеих сторон, мы узнаем $q^{*}(\mathbf {\pi } )$ как распределение Дирихле

$q^{*}(\mathbf {\pi } )\sim \operatorname {Dir} (\mathbf {\alpha } )\,$

где

$\alpha _{k}=\alpha _{0}+N_{k}\,$

где

$N_{k}=\sum _{n=1}^{N}r_{nk}\,$

Окончательно

$\ln q^{*}(\mathbf {\mu } _{k},\mathbf {\Lambda } _{k})=\ln p(\mathbf {\mu } _{k},\mathbf {\Lambda } _{k})+\sum _{n=1}^{N}\operatorname {E} [z_{nk}]\ln {\mathcal {N}}(\mathbf {x} _{n}\mid \mathbf {\mu } _{k},\mathbf {\Lambda } _{k}^{-1})+{\text{constant}}$

Группировка и чтение терминов, включающих $\mathbf {\mu } _{k}$ и $\mathbf {\Lambda } _{k}$, результатом является распределение Гаусса-Вишарта , определяемое формулой

$q^{*}(\mathbf {\mu } _{k},\mathbf {\Lambda } _{k})={\mathcal {N}}(\mathbf {\mu } _{k}\mid \mathbf {m} _{k},(\beta _{k}\mathbf {\Lambda } _{k})^{-1}){\mathcal {W}}(\mathbf {\Lambda } _{k}\mid \mathbf {W} _{k},\nu _{k})$

учитывая определения

${\begin{aligned}\beta _{k}&=\beta _{0}+N_{k}\\\mathbf {m} _{k}&={\frac {1}{\beta _{k}}}(\beta _{0}\mathbf {\mu } _{0}+N_{k}{\bar {\mathbf {x} }}_{k})\\\mathbf {W} _{k}^{-1}&=\mathbf {W} _{0}^{-1}+N_{k}\mathbf {S} _{k}+{\frac {\beta _{0}N_{k}}{\beta _{0}+N_{k}}}({\bar {\mathbf {x} }}_{k}-\mathbf {\mu } _{0})({\bar {\mathbf {x} }}_{k}-\mathbf {\mu } _{0})^{\rm {T}}\\\nu _{k}&=\nu _{0}+N_{k}\\N_{k}&=\sum _{n=1}^{N}r_{nk}\\{\bar {\mathbf {x} }}_{k}&={\frac {1}{N_{k}}}\sum _{n=1}^{N}r_{nk}\mathbf {x} _{n}\\\mathbf {S} _{k}&={\frac {1}{N_{k}}}\sum _{n=1}^{N}r_{nk}(\mathbf {x} _{n}-{\bar {\mathbf {x} }}_{k})(\mathbf {x} _{n}-{\bar {\mathbf {x} }}_{k})^{\rm {T}}\end{aligned}}$

Наконец, обратите внимание, что эти функции требуют значений $r_{nk}$, которые используют $\rho _{nk}$, который, в свою очередь, определяется на основе $\operatorname {E} [\ln \pi _{k}]$, $\operatorname {E} [\ln |\mathbf {\Lambda } _{k}|]$, и $\operatorname {E} _{\mathbf {\mu } _{k},\mathbf {\Lambda } _{k}}[(\mathbf {x} _{n}-\mathbf {\mu } _{k})^{\rm {T}}\mathbf {\Lambda } _{k}(\mathbf {x} _{n}-\mathbf {\mu } _{k})]$. Теперь, когда мы определили распределения, по которым берутся эти ожидания, мы можем вывести для них формулы:

${\begin{aligned}\operatorname {E} _{\mathbf {\mu } _{k},\mathbf {\Lambda } _{k}}[(\mathbf {x} _{n}-\mathbf {\mu } _{k})^{\rm {T}}\mathbf {\Lambda } _{k}(\mathbf {x} _{n}-\mathbf {\mu } _{k})]&=D\beta _{k}^{-1}+\nu _{k}(\mathbf {x} _{n}-\mathbf {m} _{k})^{\rm {T}}\mathbf {W} _{k}(\mathbf {x} _{n}-\mathbf {m} _{k})\\\ln {\widetilde {\Lambda }}_{k}&\equiv \operatorname {E} [\ln |\mathbf {\Lambda } _{k}|]=\sum _{i=1}^{D}\psi \left({\frac {\nu _{k}+1-i}{2}}\right)+D\ln 2+\ln |\mathbf {W} _{k}|\\\ln {\widetilde {\pi }}_{k}&\equiv \operatorname {E} \left[\ln |\pi _{k}|\right]=\psi (\alpha _{k})-\psi \left(\sum _{i=1}^{K}\alpha _{i}\right)\end{aligned}}$

Эти результаты приводят к

$r_{nk}\propto {\widetilde {\pi }}_{k}{\widetilde {\Lambda }}_{k}^{1/2}\exp \left\{-{\frac {D}{2\beta _{k}}}-{\frac {\nu _{k}}{2}}(\mathbf {x} _{n}-\mathbf {m} _{k})^{\rm {T}}\mathbf {W} _{k}(\mathbf {x} _{n}-\mathbf {m} _{k})\right\}$

Их можно преобразовать из пропорциональных в абсолютные значения путем нормализации по $k$ так что сумма соответствующих значений равна 1.

Обратите внимание, что:

1. Уравнения обновления параметров $\beta _{k}$, $\mathbf {m} _{k}$, $\mathbf {W} _{k}$ и $\nu _{k}$ переменных $\mathbf {\mu } _{k}$ и $\mathbf {\Lambda } _{k}$ зависит от статистики $N_{k}$, ${\bar {\mathbf {x} }}_{k}$, и $\mathbf {S} _{k}$, а эта статистика, в свою очередь, зависит от $r_{nk}$.
2. Уравнения обновления параметров $\alpha _{1\dots K}$ переменной $\mathbf {\pi }$ зависит от статистики $N_{k}$, что, в свою очередь, зависит от $r_{nk}$.
3. Уравнение обновления для $r_{nk}$ имеет прямую круговую зависимость от $\beta _{k}$, $\mathbf {m} _{k}$, $\mathbf {W} _{k}$ и $\nu _{k}$ а также косвенная круговая зависимость от $\mathbf {W} _{k}$, $\nu _{k}$ и $\alpha _{1\dots K}$ через ${\widetilde {\pi }}_{k}$ и ${\widetilde {\Lambda }}_{k}$.

Это предполагает итеративную процедуру, которая чередует два этапа:

1. E-шаг, который вычисляет значение $r_{nk}$ используя текущие значения всех остальных параметров.
2. M-шаг, использующий новое значение $r_{nk}$ для вычисления новых значений всех остальных параметров.

Обратите внимание, что эти шаги тесно связаны со стандартным алгоритмом EM для получения максимального правдоподобия или максимального апостериорного (MAP) решения для параметров модели гауссовой смеси . Обязанности $r_{nk}$ на этапе E близко соответствуют апостериорным вероятностям скрытых переменных с учетом данных, т.е. $p(\mathbf {Z} \mid \mathbf {X} )$; расчет статистики $N_{k}$, ${\bar {\mathbf {x} }}_{k}$, и $\mathbf {S} _{k}$ близко соответствует вычислению соответствующей статистики «мягкого подсчета» по данным; и использование этой статистики для вычисления новых значений параметров близко соответствует использованию мягких подсчетов для вычисления новых значений параметров в обычной ЭМ по модели гауссовой смеси.

Распределения экспоненциального семейства

Обратите внимание, что в предыдущем примере, когда предполагалось, что распределение по ненаблюдаемым переменным разлагается на распределения по «параметрам» и распределения по «скрытым данным», полученное «лучшее» распределение для каждой переменной находилось в том же семействе, что и соответствующее предварительное распределение по переменной. Это общий результат, который справедлив для всех предыдущих распределений, полученных из экспоненциального семейства .

См. также

• Вариационная передача сообщений : модульный алгоритм вариационного байесовского вывода.
• Вариационный автоэнкодер : искусственная нейронная сеть, принадлежащая к семействам вероятностных графических моделей и вариационных байесовских методов.
• Алгоритм ожидания-максимизации : родственный подход, который соответствует частному случаю вариационного байесовского вывода.
• Обобщенная фильтрация : вариационная схема фильтрации для нелинейных моделей в пространстве состояний.
• Вариационное исчисление : область математического анализа, занимающаяся максимизацией или минимизацией функционалов.
• Максимальная дискриминация по энтропии : это метод вариационного вывода, который позволяет вводить и учитывать дополнительные ограничения с большой прибылью.

Внешние ссылки

• Онлайн-учебник «Теория информации, вывод и алгоритмы обучения » Дэвида Дж. Маккея представляет собой введение в вариационные методы (стр. 422).
• Учебное пособие по вариационному Байесу . Фокс К. и Робертс С. 2012. Обзор искусственного интеллекта, два : 10.1007/s10462-011-9236-8 .
• Репозиторий вариационно-байесовского репозитория. Репозиторий исследовательских работ, программного обеспечения и ссылок, связанных с использованием вариационных методов для приближенного байесовского обучения до 2003 года.
• Вариационные алгоритмы для приблизительного байесовского вывода , автор М. Дж. Бил, включает сравнение EM с вариационным байесовским EM и выводы нескольких моделей, включая вариационные байесовские HMM.
• Возможно, стоит прочитать «Общее объяснение вариационного вывода» Джейсона Эйснера перед более математически подробным рассмотрением.
• Вариационный байесовский вывод копулы с помощью информационной геометрии (pdf) , Тран, В.Х., 2018. Эта статья в первую очередь написана для студентов. С помощью дивергенции Брегмана статья показывает, что вариационный Байес — это просто обобщенная пифагорейская проекция истинной модели на произвольно коррелированное (связку) пространство распределения, из которого независимое пространство является лишь частным случаем.
• Подробное введение в вариационную байесовскую заметку . Нгуен, Д. 2023 г.