нормальная обратная гамма Функция плотности вероятности
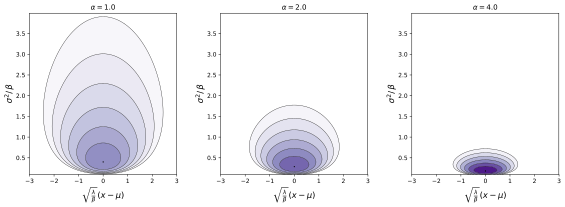
Параметры μ {\displaystyle \mu \,} местоположение ( реальное ) λ > 0 {\displaystyle \lambda >0\,} α > 0 {\displaystyle \alpha >0\,} β > 0 {\displaystyle \beta >0\,} Поддерживать x ∈ ( − ∞ , ∞ ) , σ 2 ∈ ( 0 , ∞ ) {\displaystyle x\in (-\infty ,\infty )\,\!,\;\sigma ^{2}\in (0,\infty )} PDF λ 2 π σ 2 β α Γ ( α ) ( 1 σ 2 ) α + 1 exp ( − 2 β + λ ( x − μ ) 2 2 σ 2 ) {\displaystyle {\frac {\sqrt {\lambda }}{\sqrt {2\pi \sigma ^{2}}}}{\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\left({\frac {1}{\sigma ^{2}}}\right)^{\alpha +1}\exp \left(-{\frac {2\beta +\lambda (x-\mu )^{2}}{2\sigma ^{2}}}\right)} Иметь в виду E [ x ] = μ {\displaystyle \operatorname {E} [x]=\mu }
E [ σ 2 ] = β α − 1 {\displaystyle \operatorname {E} [\sigma ^{2}]={\frac {\beta }{\alpha -1}}} α > 1 {\displaystyle \alpha >1} Режим x = μ (univariate) , x = μ (multivariate) {\displaystyle x=\mu \;{\textrm {(univariate)}},x={\boldsymbol {\mu }}\;{\textrm {(multivariate)}}}
σ 2 = β α + 1 + 1 / 2 (univariate) , σ 2 = β α + 1 + k / 2 (multivariate) {\displaystyle \sigma ^{2}={\frac {\beta }{\alpha +1+1/2}}\;{\textrm {(univariate)}},\sigma ^{2}={\frac {\beta }{\alpha +1+k/2}}\;{\textrm {(multivariate)}}} Дисперсия Var [ x ] = β ( α − 1 ) λ {\displaystyle \operatorname {Var} [x]={\frac {\beta }{(\alpha -1)\lambda }}} α > 1 {\displaystyle \alpha >1} Var [ σ 2 ] = β 2 ( α − 1 ) 2 ( α − 2 ) {\displaystyle \operatorname {Var} [\sigma ^{2}]={\frac {\beta ^{2}}{(\alpha -1)^{2}(\alpha -2)}}} α > 2 {\displaystyle \alpha >2}
Cov [ x , σ 2 ] = 0 {\displaystyle \operatorname {Cov} [x,\sigma ^{2}]=0} α > 1 {\displaystyle \alpha >1}
В теории вероятностей и статистике нормальное обратное гамма-распределение (или обратное гамма-распределение Гаусса ) представляет собой четырехпараметрическое семейство многомерных непрерывных распределений вероятностей . Это сопряженное априорное нормальное распределение с неизвестными средним значением и дисперсией .
Предполагать
x ∣ σ 2 , μ , λ ∼ N ( μ , σ 2 / λ ) {\displaystyle x\mid \sigma ^{2},\mu ,\lambda \sim \mathrm {N} (\mu ,\sigma ^{2}/\lambda )\,\!} имеет нормальное распределение со средним μ {\displaystyle \mu } дисперсия σ 2 / λ {\displaystyle \sigma ^{2}/\lambda }
σ 2 ∣ α , β ∼ Γ − 1 ( α , β ) {\displaystyle \sigma ^{2}\mid \alpha ,\beta \sim \Gamma ^{-1}(\alpha ,\beta )\!} имеет обратное гамма-распределение . Затем ( x , σ 2 ) {\displaystyle (x,\sigma ^{2})}
( x , σ 2 ) ∼ N- Γ − 1 ( μ , λ , α , β ) . {\displaystyle (x,\sigma ^{2})\sim {\text{N-}}\Gamma ^{-1}(\mu ,\lambda ,\alpha ,\beta )\!.} ( NIG {\displaystyle {\text{NIG}}} N- Γ − 1 . {\displaystyle {\text{N-}}\Gamma ^{-1}.}
Нормальное обратное распределение Уишарта представляет собой обобщение нормального обратного гамма-распределения, которое определяется для многомерных случайных величин.
f ( x , σ 2 ∣ μ , λ , α , β ) = λ σ 2 π β α Γ ( α ) ( 1 σ 2 ) α + 1 exp ( − 2 β + λ ( x − μ ) 2 2 σ 2 ) {\displaystyle f(x,\sigma ^{2}\mid \mu ,\lambda ,\alpha ,\beta )={\frac {\sqrt {\lambda }}{\sigma {\sqrt {2\pi }}}}\,{\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\,\left({\frac {1}{\sigma ^{2}}}\right)^{\alpha +1}\exp \left(-{\frac {2\beta +\lambda (x-\mu )^{2}}{2\sigma ^{2}}}\right)} Для многомерной формы, где x {\displaystyle \mathbf {x} } k × 1 {\displaystyle k\times 1}
f ( x , σ 2 ∣ μ , V − 1 , α , β ) = | V | − 1 / 2 ( 2 π ) − k / 2 β α Γ ( α ) ( 1 σ 2 ) α + 1 + k / 2 exp ( − 2 β + ( x − μ ) T V − 1 ( x − μ ) 2 σ 2 ) . {\displaystyle f(\mathbf {x} ,\sigma ^{2}\mid \mu ,\mathbf {V} ^{-1},\alpha ,\beta )=|\mathbf {V} |^{-1/2}{(2\pi )^{-k/2}}\,{\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\,\left({\frac {1}{\sigma ^{2}}}\right)^{\alpha +1+k/2}\exp \left(-{\frac {2\beta +(\mathbf {x} -{\boldsymbol {\mu }})^{T}\mathbf {V} ^{-1}(\mathbf {x} -{\boldsymbol {\mu }})}{2\sigma ^{2}}}\right).} где | V | {\displaystyle |\mathbf {V} |} определяющим фактором k × k {\displaystyle k\times k} матрица V {\displaystyle \mathbf {V} } k = 1 {\displaystyle k=1} x , V , μ {\displaystyle \mathbf {x} ,\mathbf {V} ,{\boldsymbol {\mu }}} скалярами .
Также можно позволить γ = 1 / λ {\displaystyle \gamma =1/\lambda }
f ( x , σ 2 ∣ μ , γ , α , β ) = 1 σ 2 π γ β α Γ ( α ) ( 1 σ 2 ) α + 1 exp ( − 2 γ β + ( x − μ ) 2 2 γ σ 2 ) {\displaystyle f(x,\sigma ^{2}\mid \mu ,\gamma ,\alpha ,\beta )={\frac {1}{\sigma {\sqrt {2\pi \gamma }}}}\,{\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\,\left({\frac {1}{\sigma ^{2}}}\right)^{\alpha +1}\exp \left(-{\frac {2\gamma \beta +(x-\mu )^{2}}{2\gamma \sigma ^{2}}}\right)} В многомерной форме соответствующим изменением будет учет ковариационной матрицы V {\displaystyle \mathbf {V} } обратного V − 1 {\displaystyle \mathbf {V} ^{-1}}
F ( x , σ 2 ∣ μ , λ , α , β ) = e − β σ 2 ( β σ 2 ) α ( erf ( λ ( x − μ ) 2 σ ) + 1 ) 2 σ 2 Γ ( α ) {\displaystyle F(x,\sigma ^{2}\mid \mu ,\lambda ,\alpha ,\beta )={\frac {e^{-{\frac {\beta }{\sigma ^{2}}}}\left({\frac {\beta }{\sigma ^{2}}}\right)^{\alpha }\left(\operatorname {erf} \left({\frac {{\sqrt {\lambda }}(x-\mu )}{{\sqrt {2}}\sigma }}\right)+1\right)}{2\sigma ^{2}\Gamma (\alpha )}}} Данный ( x , σ 2 ) ∼ N- Γ − 1 ( μ , λ , α , β ) . {\displaystyle (x,\sigma ^{2})\sim {\text{N-}}\Gamma ^{-1}(\mu ,\lambda ,\alpha ,\beta )\!.} σ 2 {\displaystyle \sigma ^{2}} обратному гамма-распределению :
σ 2 ∼ Γ − 1 ( α , β ) {\displaystyle \sigma ^{2}\sim \Gamma ^{-1}(\alpha ,\beta )\!} пока α λ β ( x − μ ) {\displaystyle {\sqrt {\frac {\alpha \lambda }{\beta }}}(x-\mu )} t-распределению с 2 α {\displaystyle 2\alpha } [1]
Доказательство λ = 1 {\displaystyle \lambda =1} Для λ = 1 {\displaystyle \lambda =1}
f ( x , σ 2 ∣ μ , α , β ) = 1 σ 2 π β α Γ ( α ) ( 1 σ 2 ) α + 1 exp ( − 2 β + ( x − μ ) 2 2 σ 2 ) {\displaystyle f(x,\sigma ^{2}\mid \mu ,\alpha ,\beta )={\frac {1}{\sigma {\sqrt {2\pi }}}}\,{\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\,\left({\frac {1}{\sigma ^{2}}}\right)^{\alpha +1}\exp \left(-{\frac {2\beta +(x-\mu )^{2}}{2\sigma ^{2}}}\right)}
Маргинальное распределение по x {\displaystyle x}
f ( x ∣ μ , α , β ) = ∫ 0 ∞ d σ 2 f ( x , σ 2 ∣ μ , α , β ) = 1 2 π β α Γ ( α ) ∫ 0 ∞ d σ 2 ( 1 σ 2 ) α + 1 / 2 + 1 exp ( − 2 β + ( x − μ ) 2 2 σ 2 ) {\displaystyle {\begin{aligned}f(x\mid \mu ,\alpha ,\beta )&=\int _{0}^{\infty }d\sigma ^{2}f(x,\sigma ^{2}\mid \mu ,\alpha ,\beta )\\&={\frac {1}{\sqrt {2\pi }}}\,{\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\int _{0}^{\infty }d\sigma ^{2}\left({\frac {1}{\sigma ^{2}}}\right)^{\alpha +1/2+1}\exp \left(-{\frac {2\beta +(x-\mu )^{2}}{2\sigma ^{2}}}\right)\end{aligned}}}
За исключением нормировочного коэффициента, выражение под интегралом совпадает с обратным гамма-распределением.
Γ − 1 ( x ; a , b ) = b a Γ ( a ) e − b / x x a + 1 , {\displaystyle \Gamma ^{-1}(x;a,b)={\frac {b^{a}}{\Gamma (a)}}{\frac {e^{-b/x}}{{x}^{a+1}}},}
с x = σ 2 {\displaystyle x=\sigma ^{2}} a = α + 1 / 2 {\displaystyle a=\alpha +1/2} b = 2 β + ( x − μ ) 2 2 {\displaystyle b={\frac {2\beta +(x-\mu )^{2}}{2}}}
С ∫ 0 ∞ d x Γ − 1 ( x ; a , b ) = 1 , ∫ 0 ∞ d x x − ( a + 1 ) e − b / x = Γ ( a ) b − a {\displaystyle \int _{0}^{\infty }dx\Gamma ^{-1}(x;a,b)=1,\quad \int _{0}^{\infty }dxx^{-(a+1)}e^{-b/x}=\Gamma (a)b^{-a}}
∫ 0 ∞ d σ 2 ( 1 σ 2 ) α + 1 / 2 + 1 exp ( − 2 β + ( x − μ ) 2 2 σ 2 ) = Γ ( α + 1 / 2 ) ( 2 β + ( x − μ ) 2 2 ) − ( α + 1 / 2 ) {\displaystyle \int _{0}^{\infty }d\sigma ^{2}\left({\frac {1}{\sigma ^{2}}}\right)^{\alpha +1/2+1}\exp \left(-{\frac {2\beta +(x-\mu )^{2}}{2\sigma ^{2}}}\right)=\Gamma (\alpha +1/2)\left({\frac {2\beta +(x-\mu )^{2}}{2}}\right)^{-(\alpha +1/2)}}
Подставив это выражение и факторизовав зависимость от x {\displaystyle x}
f ( x ∣ μ , α , β ) ∝ x ( 1 + ( x − μ ) 2 2 β ) − ( α + 1 / 2 ) . {\displaystyle f(x\mid \mu ,\alpha ,\beta )\propto _{x}\left(1+{\frac {(x-\mu )^{2}}{2\beta }}\right)^{-(\alpha +1/2)}.}
Форма обобщенного t-распределения Стьюдента :
t ( x | ν , μ ^ , σ ^ 2 ) ∝ x ( 1 + 1 ν ( x − μ ^ ) 2 σ ^ 2 ) − ( ν + 1 ) / 2 {\displaystyle t(x|\nu ,{\hat {\mu }},{\hat {\sigma }}^{2})\propto _{x}\left(1+{\frac {1}{\nu }}{\frac {(x-{\hat {\mu }})^{2}}{{\hat {\sigma }}^{2}}}\right)^{-(\nu +1)/2}}
Маргинальное распределение f ( x ∣ μ , α , β ) {\displaystyle f(x\mid \mu ,\alpha ,\beta )} 2 α {\displaystyle 2\alpha }
f ( x ∣ μ , α , β ) = t ( x | ν = 2 α , μ ^ = μ , σ ^ 2 = β / α ) {\displaystyle f(x\mid \mu ,\alpha ,\beta )=t(x|\nu =2\alpha ,{\hat {\mu }}=\mu ,{\hat {\sigma }}^{2}=\beta /\alpha )}
В многомерном случае предельное распределение x {\displaystyle \mathbf {x} } многомерное распределение t :
x ∼ t 2 α ( μ , β α V ) {\displaystyle \mathbf {x} \sim t_{2\alpha }({\boldsymbol {\mu }},{\frac {\beta }{\alpha }}\mathbf {V} )\!} Предполагать
( x , σ 2 ) ∼ N- Γ − 1 ( μ , λ , α , β ) . {\displaystyle (x,\sigma ^{2})\sim {\text{N-}}\Gamma ^{-1}(\mu ,\lambda ,\alpha ,\beta )\!.} Тогда для c > 0 {\displaystyle c>0}
( c x , c σ 2 ) ∼ N- Γ − 1 ( c μ , λ / c , α , c β ) . {\displaystyle (cx,c\sigma ^{2})\sim {\text{N-}}\Gamma ^{-1}(c\mu ,\lambda /c,\alpha ,c\beta )\!.} Доказательство: Чтобы доказать это, пусть ( x , σ 2 ) ∼ N- Γ − 1 ( μ , λ , α , β ) {\displaystyle (x,\sigma ^{2})\sim {\text{N-}}\Gamma ^{-1}(\mu ,\lambda ,\alpha ,\beta )} c > 0 {\displaystyle c>0} Y = ( Y 1 , Y 2 ) = ( c x , c σ 2 ) {\displaystyle Y=(Y_{1},Y_{2})=(cx,c\sigma ^{2})} Y {\displaystyle Y} ( y 1 , y 2 ) {\displaystyle (y_{1},y_{2})} 1 / c 2 {\displaystyle 1/c^{2}} N- Γ − 1 ( μ , λ , α , β ) {\displaystyle {\text{N-}}\Gamma ^{-1}(\mu ,\lambda ,\alpha ,\beta )} ( y 1 / c , y 2 / c ) {\displaystyle (y_{1}/c,y_{2}/c)} Y {\displaystyle Y} ( y 1 , y 2 ) {\displaystyle (y_{1},y_{2})} f Y ( y 1 , y 2 ) = 1 c 2 λ 2 π y 2 / c β α Γ ( α ) ( 1 y 2 / c ) α + 1 exp ( − 2 β + λ ( y 1 / c − μ ) 2 2 y 2 / c ) = λ / c 2 π y 2 ( c β ) α Γ ( α ) ( 1 y 2 ) α + 1 exp ( − 2 c β + ( λ / c ) ( y 1 − c μ ) 2 2 y 2 ) . {\displaystyle f_{Y}(y_{1},y_{2})={\frac {1}{c^{2}}}{\frac {\sqrt {\lambda }}{\sqrt {2\pi y_{2}/c}}}\,{\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\,\left({\frac {1}{y_{2}/c}}\right)^{\alpha +1}\exp \left(-{\frac {2\beta +\lambda (y_{1}/c-\mu )^{2}}{2y_{2}/c}}\right)={\frac {\sqrt {\lambda /c}}{\sqrt {2\pi y_{2}}}}\,{\frac {(c\beta )^{\alpha }}{\Gamma (\alpha )}}\,\left({\frac {1}{y_{2}}}\right)^{\alpha +1}\exp \left(-{\frac {2c\beta +(\lambda /c)\,(y_{1}-c\mu )^{2}}{2y_{2}}}\right).\!}
Правое выражение — это PDF-файл для N- Γ − 1 ( c μ , λ / c , α , c β ) {\displaystyle {\text{N-}}\Gamma ^{-1}(c\mu ,\lambda /c,\alpha ,c\beta )} ( y 1 , y 2 ) {\displaystyle (y_{1},y_{2})}
Распределения нормального обратного гамма-распределения образуют экспоненциальное семейство с натуральными параметрами. θ 1 = − λ 2 {\displaystyle \textstyle \theta _{1}={\frac {-\lambda }{2}}} θ 2 = λ μ {\displaystyle \textstyle \theta _{2}=\lambda \mu } θ 3 = α {\displaystyle \textstyle \theta _{3}=\alpha } θ 4 = − β + − λ μ 2 2 {\displaystyle \textstyle \theta _{4}=-\beta +{\frac {-\lambda \mu ^{2}}{2}}} T 1 = x 2 σ 2 {\displaystyle \textstyle T_{1}={\frac {x^{2}}{\sigma ^{2}}}} T 2 = x σ 2 {\displaystyle \textstyle T_{2}={\frac {x}{\sigma ^{2}}}} T 3 = log ( 1 σ 2 ) {\displaystyle \textstyle T_{3}=\log {\big (}{\frac {1}{\sigma ^{2}}}{\big )}} T 4 = 1 σ 2 {\displaystyle \textstyle T_{4}={\frac {1}{\sigma ^{2}}}}
Измеряет разницу между двумя распределениями.
См. статьи о нормальном гамма-распределении и сопряженном априорном .
См. статьи о нормальном гамма-распределении и сопряженном априорном .
Генерация случайных величин нормальной-обратной гаммы [ редактировать ] Генерация случайных величин проста:
Образец σ 2 {\displaystyle \sigma ^{2}} α {\displaystyle \alpha } β {\displaystyle \beta } Образец x {\displaystyle x} μ {\displaystyle \mu } σ 2 / λ {\displaystyle \sigma ^{2}/\lambda } Нормальное гамма-распределение — это то же распределение, параметризованное точностью , а не дисперсией. Обобщение этого распределения, которое учитывает многомерное среднее и совершенно неизвестную положительно определенную ковариационную матрицу. σ 2 V {\displaystyle \sigma ^{2}\mathbf {V} } σ 2 {\displaystyle \sigma ^{2}} нормальное обратное распределение Уишарта. Денисон, Дэвид Г.Т.; Холмс, Кристофер С.; Маллик, Бани К.; Смит, Адриан Ф.М. (2002) Байесовские методы нелинейной классификации и регрессии , Wiley. ISBN 0471490369 Кох, Карл-Рудольф (2007) Введение в байесовскую статистику (2-е издание), Springer. ISBN 354072723X
скрывать Дискретный
с конечным с бесконечным
Непрерывный
поддерживается на поддерживается на поддерживается при поддержке
Смешанный
Многомерный Направленный Выродиться единственное число Семьи






![{\displaystyle \operatorname {E} [x]=\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d60f5921cca1c75d673eb70db395bf3a88f9170f)
![{\displaystyle \operatorname {E} [\sigma ^{2}]={\frac {\beta }{\alpha -1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b74baba053fd81d56d62de618558ac7af62ade55)



![{\displaystyle \operatorname {Var} [x]={\frac {\beta }{(\alpha -1)\lambda }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c11eddb529a936912263edfb0c46ce2a42adfbd5)
![{\displaystyle \operatorname {Var} [\sigma ^{2}]={\frac {\beta ^{2}}{(\alpha -1)^{2}(\alpha -2)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d089f3b7da4ce1f13940b4731eb531932850d0e)

![{\displaystyle \operatorname {Cov} [x,\sigma ^{2}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7006f5738ee174c6c35e1694f1c4ac3b2c9c42)





























































