Многогранник Шёнхардта

Многогранник Шёнхардта
Многогранник Шёнхардта
Лица	8
Края	12
Вершины	6
Характеристики	невыпуклый ; нет внутренних диагоналей ; не может быть триангулирован
Сеть

В геометрии многогранник Шенхардта — это многогранник с той же комбинаторной структурой, что и правильный октаэдр , но с двугранными углами , невыпуклыми вдоль трех непересекающихся ребер. Поскольку у него нет внутренних диагоналей , его нельзя разбить на тетраэдры без добавления новых вершин. У него наименьшее количество вершин среди всех многогранников, которые нельзя триангулировать. Она названа в честь немецкого математика Эриха Шенхардта , который описал ее в 1928 году, хотя художник Карлис Йохансонс продемонстрировал похожую структуру в 1921 году.

Одна конструкция многогранника Шенхардта начинается с треугольной призмы и скручивает две равносторонние треугольные грани призмы относительно друг друга, разбивая каждую квадратную грань на два треугольника, разделенных невыпуклым краем. Некоторые углы поворота создают прыгающий многогранник , две твердые формы которого имеют одинаковые формы граней. Вместо этого поворот на 30° создает шаткий многогранник , жесткий, но не бесконечно жесткий , края которого образуют призму тенсегрити .

Многогранники Шёнхардта использовались в качестве приспособлений для доказательства того, что проверка того, имеет ли многогранник триангуляцию, является NP-полной . Несколько других многогранников, включая икосаэдр Йессена , разделяют с многогранником Шенхардта свойства отсутствия триангуляции, прыжков или шаткости, а также формирования структуры тенсегрити.

Строительство

Один из способов построения многогранника Шенхардта начинается с треугольной призмы с двумя параллельными равносторонними треугольниками в качестве ее граней. Один из треугольников повернут вокруг центральной линии призмы. Угол поворота является произвольным параметром, который можно плавно изменять. ^{[ 1 ]} В результате этого вращения квадратные грани треугольника превращаются в косые многоугольники , каждый из которых можно повторно триангулировать с помощью двух треугольников, чтобы сформировать либо выпуклый, либо невыпуклый двугранный угол . Когда все три пары треугольников выбраны так, чтобы иметь невыпуклый двугранник, в результате получается многогранник Шенхардта. ^{[ 2 ]}

Характеристики

Многогранник Шёнхардта имеет шесть вершин, двенадцать ребер и восемь треугольных граней. Его шесть вершин образуют пятнадцать неупорядоченных пар. Двенадцать из этих пятнадцати пар образуют ребра многогранника: шесть ребер находятся в двух гранях равностороннего треугольника и шесть ребер соединяют два треугольника. Остальные три пары образуют диагонали многогранника, но целиком лежат вне многогранника. ^{[ 3 ]}

Выпуклая оболочка многогранника Шенхардта — это еще один многогранник с теми же шестью вершинами и другим набором из двенадцати ребер и восьми треугольных граней. И эта оболочка, и сам многогранник Шёнхардта комбинаторно эквивалентны правильному октаэдру . Симметричная разность оболочки и многогранника Шенхардта состоит из трех тетраэдров, каждый из которых лежит между одним из вогнутых двугранных ребер многогранника Шенхардта и одной из внешних диагоналей. Таким образом, многогранник Шенхардта можно образовать, удалив эти три тетраэдра из выпуклого (но неправильного) октаэдра. ^{[ 4 ]}

Невозможность триангуляции

Триангуляция тетраэдры многогранника — это разбиение на , встречающиеся лицом к лицу и использующие только вершины данного многогранника. В этом смысле каждый выпуклый многогранник имеет триангуляцию, а многогранник Шенхардта - нет. Среди многогранников, не имеющих триангуляции, он имеет наименьшее количество вершин. ^{[ 1 ]}

Более того, ни один тетраэдр не лежит целиком внутри многогранника Шенхардта и не разделяет с ним все четыре вершины. Это следует из следующих двух свойств многогранника Шенхардта : ^{[ 3 ]}

Каждый треугольник, образованный его ребрами, является одной из его граней. Следовательно, поскольку он сам по себе не является тетраэдром, каждый тетраэдр, образованный четырьмя его вершинами, должен иметь ребро, которое не является общим с многогранником Шенхардта. ^{[ 3 ]}
Каждая диагональ, соединяющая две его вершины, но не являющаяся ребром многогранника Шенхардта, лежит вне многогранника. Следовательно, каждый тетраэдр, использующий такую диагональ в качестве одного из своих ребер, также должен частично лежать вне многогранника Шенхардта. ^{[ 3 ]}

Стабильность

Некоторые экземпляры многогранника Шенхардта образуют прыгающий многогранник : многогранник, который имеет два разных жестких состояния, оба имеют одинаковую форму граней и одинаковую ориентацию (выпуклую или вогнутую) каждого края. Модель, поверхность которой сделана из жесткого, но несколько деформируемого материала, например картона, может «перепрыгивать» между двумя формами. Твердотельная модель не могла изменить форму таким образом. Не смогла бы и модель, сделанная из более жесткого материала, такого как стекло: хотя она могла существовать в любой из двух форм, она не могла бы достаточно деформироваться, чтобы перемещаться между ними. ^{[ 5 ]} Это противоречит теореме Коши о жесткости , согласно которой для каждого выпуклого многогранника не существует другого многогранника с такой же формой граней и ориентацией ребер. ^{[ 6 ]}

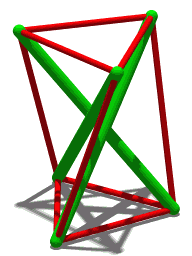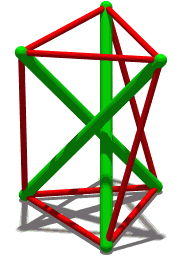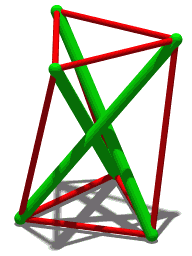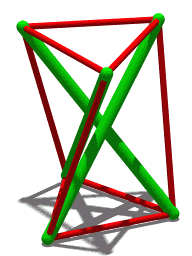
Тенсегрити с тремя элементами сжатия (зеленые) и девятью элементами растяжения (красные). Призма ^{[ 7 ]}

Кадр из фильма «Пространственные конструкции» (1921) Карлиса Йохансонса , показывающий призму тенсегрити.

В своей первоначальной работе об этом многограннике Шенхардт отметил связанное с этим свойство: в одной особой форме, когда две равносторонние грани скручены под углом 30° друг к другу, этот многогранник становится шатким : жестким по отношению к непрерывному движению, но не бесконечно твердый . ^{[ 1 ]} При этом же угле поворота в 30° ребра многогранника Шенхардта можно использовать для формирования структуры тенсегрити, называемой призмой тенсегрити , с элементами сжатия для ее невыпуклых краев и элементами растяжения для ее выпуклых краев. ^{[ 7 ]} Открытие этой формы как структуры тенсегрити, а не как многогранника, приписывают латвийско-советскому художнику Карлису Йохансонсу в 1921 году, за несколько лет до работ Шенхардта. ^{[ 8 ]}

Приложения

Рупперт и Зайдель (1992) использовали многогранник Шенхардта в качестве основы для доказательства его NP-полноты , чтобы определить, можно ли триангулировать невыпуклый многогранник. В доказательстве используется множество копий многогранника Шенхардта с удаленной верхней гранью в качестве приспособлений внутри большего многогранника. Любая триангуляция всего многогранника должна включать тетраэдр, соединяющий нижнюю грань каждого гаджета с вершиной в остальной части многогранника, которая может видеть эту нижнюю грань. Сложная структура препятствий между тетраэдрами этого типа может быть использована для моделирования булевой логики компонентов в результате сокращения проблемы булевой выполнимости . ^{[ 4 ]}^{[ 9 ]}

Связанные конструкции

Открытие Шенхардтом этого многогранника в 1928 году было вызвано более ранней работой Нельса Иоганна Леннеса, который опубликовал в 1911 году многогранник с семью вершинами без триангуляции. ^{[ 1 ]}^{[ 10 ]}^{[ 11 ]}

Так же как и прыгающие, невыпуклые многогранники могут быть гибкими , имея непрерывное семейство фигур с одинаковыми гранями. ^{[ 6 ]} Октаэдры Брикара в этом смысле гибкие, имеют ту же комбинаторную структуру, что и многогранник Шенхардта, но в отличие от многогранника Шенхардта они являются самопересекающимися. ^{[ 12 ]}

было показано, Рамбау (2005) что многогранник Шёнхардта можно обобщить на другие многогранники, комбинаторно эквивалентные антипризмам , которые не могут быть триангулированы. Эти многогранники образуются путем соединения правильных $k$ -угольники в двух параллельных плоскостях, закрученные друг относительно друга так, что $k$ принадлежащий $2k$ края, соединяющие два $k$ -угольники имеют вогнутые двугранники. При достаточно малых углах закручивания результат не имеет триангуляции. ^{[ 4 ]}^{[ 13 ]} Другой многогранник, который не может быть триангулирован, — это икосаэдр Джессена , который комбинаторно эквивалентен правильному икосаэдру . ^{[ 2 ]} и (как и тенсегрити-форма многогранника Шёнхардта) также шаткая тенсегрити. ^{[ 14 ]}

В другом направлении Багемиль (1948) построил семейство многогранников, которые разделяют с многогранником Шенхардта то свойство, что нет внутренних диагоналей . Тетраэдр вообще не имеют диагоналей: каждая пара вершин в этих многогранниках и многогранник Часара образует ребро. ^{[ 3 ]} Остается открытым вопрос, существуют ли еще многогранники (с краем многообразия ) без диагоналей, ^{[ 15 ]} хотя существуют поверхности немногообразия без диагоналей и с любым количеством вершин, большим пяти. ^{[ 16 ]}

Ссылки

^ Перейти обратно: ^а ^б ^с ^д Шенхардт, Э. (1928), «О разложении треугольных многогранников на тетраэдры» , Mathematical Annals , 98 : 309–312, doi : 10.1007/BF01451597
^ Перейти обратно: ^а ^б Бездек, Андрас; Кэрриган, Брэкстон (2016), «О нетреугольных многогранниках», Вклад в алгебру и геометрию , 57 (1): 51–66, doi : 10.1007/s13366-015-0248-4 , MR 3457762 , S2CID 118484882
^ Перейти обратно: ^а ^б ^с ^д ^и Багемил, Ф. (1948), «О неразложимых многогранниках», American Mathematical Monthly , 55 (7): 411–413, doi : 10.2307/2306130 , JSTOR 2306130
^ Перейти обратно: ^а ^б ^с Де Лоэра, Хесус А .; Рамбау, Йорг; Сантос, Франциско (2010), «Пример 3.6.1: Многогранник Шенхардта», Триангуляции: структуры для алгоритмов и приложений , Алгоритмы и вычисления в математике, том. 25, Берлин: Springer-Verlag, стр. 133–134, номер домена : 10.1007/978-3-642-12971-1 , ISBN. 978-3-642-12970-4 , МР 2743368
^ Грюнбаум, Бранко (1975), Лекции по утраченной математике (PDF) , стр. 41–42.
^ Перейти обратно: ^а ^б Айгнер, Мартин ; Циглер, Гюнтер М. (2018), «Глава 14: Теорема о жесткости Коши», Доказательства из КНИГИ (6-е изд.), Springer, стр. 95–98, doi : 10.1007/978-3-662-57265-8_15 , ISBN 978-3-662-57265-8
^ Перейти обратно: ^а ^б Ван, Бин-Бин; Лю, Си-Лян (декабрь 1996 г.), «Исследование интегрального напряжения в двухслойных тенсегрити-сетках», Международный журнал космических структур , 11 (4): 349–355, doi : 10.1177/026635119601100401
^ Бансод, Йогеш Дипак; Нанданвар, Дипеш; Бурша, Иржи (2014), «Обзор тенсегрити – I: Основные структуры» (PDF) , Инженерная механика , 21 (5): 355–367
^ Руперт, Дж.; Зайдель, Р. (1992), «О сложности триангуляции трехмерных невыпуклых многогранников», Discrete & Computational Geometry , 7 (3): 227–253, doi : 10.1007/BF02187840
^ Леннес, Нью-Джерси (январь 1911 г.), «Теоремы о простом конечном многоугольнике и многограннике», American Journal of Mathematics , 33 (1/4): 37–62, doi : 10.2307/2369986 , JSTOR 2369986
^ «Модель многогранника Ленна, автор Ричард П. Бейкер, Baker № 287» , Коллекции , Национальный музей американской истории , получено 18 февраля 2024 г.
^ Коннелли, Роберт (1981), «Гибкие поверхности», в Кларнере, Дэвиде А. (редактор), The Mathematical Gardner , Springer, стр. 79–89, doi : 10.1007/978-1-4684-6686-7_10 , ISBN 978-1-4684-6688-1 .
^ Рамбау, Дж. (2005), «Об обобщении многогранника Шенхардта» (PDF) , в Гудмане, Джейкоб Э .; Пах, Янош ; Вельцль, Эмо (ред.), Комбинаторная и вычислительная геометрия , Публикации ИИГС, том. 52, Кембридж: Издательство Кембриджского университета, стр. 501–516.
^ Гольдберг, Майкл (1978), «Нестабильные многогранные структуры», Mathematics Magazine , 51 (3): 165–170, doi : 10.2307/2689996 , JSTOR 2689996 , MR 0498579
^ Циглер, Гюнтер М. (2008), «Многогранные поверхности высокого рода», Бобенко, А.И.; Шредер, П.; Салливан, Дж. М .; и др. (ред.), Дискретная дифференциальная геометрия , Семинары в Обервольфахе, том. 38, Springer-Verlag, стр. 191–213, arXiv : math/0412093 , doi : 10.1007/978-3-7643-8621-4_10 , ISBN 978-3-7643-8620-7 , math.MG/0412093
^ Сабо, Шандор (1984), «Многогранники без диагоналей», Periodica Mathematica Hungarica , 15 (1): 41–49, doi : 10.1007/BF02109370 ; Сабо, Шандор (2009), «Многогранники без диагоналей II», Periodica Mathematica Hungarica , 58 (2): 181–187, doi : 10.1007/s10998-009-10181-x

Внешние ссылки

Многогранник Шенхардта , mathgrrl , включая ссылки на бесплатную модель для 3D-печати

[schonhardt-1] Перейти обратно: ^а ^б ^с ^д Шенхардт, Э. (1928), «О разложении треугольных многогранников на тетраэдры» , Mathematical Annals , 98 : 309–312, doi : 10.1007/BF01451597

[bezdek-carrigan-2] Перейти обратно: ^а ^б Бездек, Андрас; Кэрриган, Брэкстон (2016), «О нетреугольных многогранниках», Вклад в алгебру и геометрию , 57 (1): 51–66, doi : 10.1007/s13366-015-0248-4 , MR 3457762 , S2CID 118484882

[bagemihl-3] Перейти обратно: ^а ^б ^с ^д ^и Багемил, Ф. (1948), «О неразложимых многогранниках», American Mathematical Monthly , 55 (7): 411–413, doi : 10.2307/2306130 , JSTOR 2306130

[deloera-rambau-santos-4] Перейти обратно: ^а ^б ^с Де Лоэра, Хесус А .; Рамбау, Йорг; Сантос, Франциско (2010), «Пример 3.6.1: Многогранник Шенхардта», Триангуляции: структуры для алгоритмов и приложений , Алгоритмы и вычисления в математике, том. 25, Берлин: Springer-Verlag, стр. 133–134, номер домена : 10.1007/978-3-642-12971-1 , ISBN. 978-3-642-12970-4 , МР 2743368

[grunbaum-5] Грюнбаум, Бранко (1975), Лекции по утраченной математике (PDF) , стр. 41–42.

[az-6] Перейти обратно: ^а ^б Айгнер, Мартин ; Циглер, Гюнтер М. (2018), «Глава 14: Теорема о жесткости Коши», Доказательства из КНИГИ (6-е изд.), Springer, стр. 95–98, doi : 10.1007/978-3-662-57265-8_15 , ISBN 978-3-662-57265-8

[wangliu-7] Перейти обратно: ^а ^б Ван, Бин-Бин; Лю, Си-Лян (декабрь 1996 г.), «Исследование интегрального напряжения в двухслойных тенсегрити-сетках», Международный журнал космических структур , 11 (4): 349–355, doi : 10.1177/026635119601100401

[bnb-8] Бансод, Йогеш Дипак; Нанданвар, Дипеш; Бурша, Иржи (2014), «Обзор тенсегрити – I: Основные структуры» (PDF) , Инженерная механика , 21 (5): 355–367

[ruppert-seidel-9] Руперт, Дж.; Зайдель, Р. (1992), «О сложности триангуляции трехмерных невыпуклых многогранников», Discrete & Computational Geometry , 7 (3): 227–253, doi : 10.1007/BF02187840

[lennes-10] Леннес, Нью-Джерси (январь 1911 г.), «Теоремы о простом конечном многоугольнике и многограннике», American Journal of Mathematics , 33 (1/4): 37–62, doi : 10.2307/2369986 , JSTOR 2369986

[nmah-11] «Модель многогранника Ленна, автор Ричард П. Бейкер, Baker № 287» , Коллекции , Национальный музей американской истории , получено 18 февраля 2024 г.

[connelly-12] Коннелли, Роберт (1981), «Гибкие поверхности», в Кларнере, Дэвиде А. (редактор), The Mathematical Gardner , Springer, стр. 79–89, doi : 10.1007/978-1-4684-6686-7_10 , ISBN 978-1-4684-6688-1 .

[rambau-13] Рамбау, Дж. (2005), «Об обобщении многогранника Шенхардта» (PDF) , в Гудмане, Джейкоб Э .; Пах, Янош ; Вельцль, Эмо (ред.), Комбинаторная и вычислительная геометрия , Публикации ИИГС, том. 52, Кембридж: Издательство Кембриджского университета, стр. 501–516.

[goldberg-14] Гольдберг, Майкл (1978), «Нестабильные многогранные структуры», Mathematics Magazine , 51 (3): 165–170, doi : 10.2307/2689996 , JSTOR 2689996 , MR 0498579

[ziegler-15] Циглер, Гюнтер М. (2008), «Многогранные поверхности высокого рода», Бобенко, А.И.; Шредер, П.; Салливан, Дж. М .; и др. (ред.), Дискретная дифференциальная геометрия , Семинары в Обервольфахе, том. 38, Springer-Verlag, стр. 191–213, arXiv : math/0412093 , doi : 10.1007/978-3-7643-8621-4_10 , ISBN 978-3-7643-8620-7 , math.MG/0412093

[szabo-16] Сабо, Шандор (1984), «Многогранники без диагоналей», Periodica Mathematica Hungarica , 15 (1): 41–49, doi : 10.1007/BF02109370 ; Сабо, Шандор (2009), «Многогранники без диагоналей II», Periodica Mathematica Hungarica , 58 (2): 181–187, doi : 10.1007/s10998-009-10181-x

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]