Сходство (сетевая наука)
Эта статья нуждается в дополнительных цитатах для проверки . ( май 2014 г. ) |
| Часть серии о | ||||
| Сетевая наука | ||||
|---|---|---|---|---|
| Типы сетей | ||||
| Графики | ||||
| ||||
| Модели | ||||
| ||||
| ||||
Сходство в сетевом анализе возникает, когда два узла (или другие более сложные структуры) попадают в один и тот же класс эквивалентности.
Существует три фундаментальных подхода к построению мер сетевого сходства: структурная эквивалентность, автоморфная эквивалентность и регулярная эквивалентность. [1] Существует иерархия трех концепций эквивалентности: любой набор структурных эквивалентностей также является автоморфной и регулярной эквивалентностью. Любой набор автоморфных эквивалентностей также является регулярной эквивалентностью. Не все регулярные эквивалентности обязательно автоморфны или структурны; и не все автоморфные эквивалентности обязательно являются структурными. [2]
Визуализация сходства и расстояния [ править ]
Инструменты кластеризации [ править ]
Агломеративная иерархическая кластеризация узлов на основе сходства их профилей связей с другими узлами обеспечивает дерево соединений или дендрограмму , которая визуализирует степень сходства между случаями и может использоваться для поиска приблизительных классов эквивалентности. [2]
Инструменты многомерного масштабирования [ править ]
Обычно наша цель анализа эквивалентности — идентифицировать и визуализировать «классы» или группы случаев. При использовании кластерного анализа мы неявно предполагаем, что сходство или расстояние между случаями отражает одно основное измерение. Однако возможно, что за наблюдаемым сходством дел стоит множество «аспектов» или «аспектов». Факторный или компонентный анализ может быть применен к корреляциям или ковариациям между случаями. В качестве альтернативы можно использовать многомерное масштабирование (неметрическое для данных, которые по своей сути являются номинальными или порядковыми; метрическое для значимых). [2]
MDS представляет закономерности сходства или несходства в профилях связи между участниками (применительно к смежности или расстояниям) в виде «карты» в многомерном пространстве. Эта карта позволяет нам увидеть, насколько «близки» действующие лица, «группируются» ли они в многомерном пространстве и насколько велики различия по каждому измерению. [2]
эквивалентность Структурная
Две вершины сети структурно эквивалентны, если у них много одинаковых соседей.

Не существует актера, у которого был бы точно такой же набор связей, как у актера А, поэтому актер А сам принадлежит к классу. То же самое верно и для актеров B, C, D и G. Каждый из этих узлов имеет уникальный набор ребер для других узлов. Однако E и F относятся к одному и тому же классу структурной эквивалентности. У каждого есть только одно ребро; и эта связь связана с B. Поскольку E и F имеют одинаковый набор ребер со всеми вершинами, они структурно эквивалентны. То же самое верно и в случае H и I. [2]
Структурная эквивалентность — самая сильная форма сходства. Во многих реальных сетях точная эквивалентность может быть редкостью, и было бы полезно облегчить критерии и измерить приблизительную эквивалентность.
Тесно связанной концепцией является институциональная эквивалентность : два субъекта (например, фирмы) институционально эквивалентны, если они действуют в одном и том же наборе институциональных полей. [3] Хотя структурно эквивалентные акторы имеют идентичные модели отношений или сетевые позиции, институциональная эквивалентность отражает сходство институциональных влияний, которые акторы испытывают, находясь в одних и тех же полях, независимо от того, насколько схожи их сетевые позиции. Например, два банка в Чикаго могут иметь совершенно разные модели связей (например, один может быть центральным узлом, а другой может находиться на периферии), так что они не являются структурными эквивалентами, но поскольку они оба действуют в поле финансов и банковского дела и в одной и той же географически определенной области (Чикаго) они будут подвержены некоторым одинаковым институциональным влияниям. [3]
Меры структурной эквивалентности
Косинусное подобие [ править ]
Простой подсчет общих соседей для двух вершин сам по себе не очень хороший показатель. Необходимо знать степень вершин или количество общих соседей у других пар вершин. Косинусное сходство учитывает эти аспекты, а также допускает различную степень вершин. Солтон предложил рассматривать i-ю и j-ю строки/столбцы матрицы смежности как два вектора и использовать косинус угла между ними в качестве меры сходства . Косинусное подобие i и j — это количество общих соседей, деленное на среднее геометрическое их степеней. [4]
Его значение лежит в диапазоне от 0 до 1. Значение 1 указывает, что две вершины имеют одинаковых соседей, а значение ноль означает, что у них нет общих соседей. Косинусное сходство технически не определено, если один или оба узла имеют нулевую степень, но согласно соглашению мы говорим, что в этих случаях косинусное сходство равно 0. [1]
Пирсона Коэффициент
Коэффициент корреляции момента произведения Пирсона - это альтернативный метод нормализации количества общих соседей. Этот метод сравнивает количество общих соседей с ожидаемым значением, которое счетчик принял бы в сети, где вершины соединены случайным образом. Эта величина лежит строго в диапазоне от -1 до 1. [1]
Евклидово расстояние [ править ]
Евклидово расстояние равно количеству соседей, различающихся между двумя вершинами. Это скорее мера несходства, поскольку она больше для вершин, которые различаются сильнее. Его можно нормализовать, разделив на максимальное значение. Максимум означает, что общих соседей нет, и в этом случае расстояние равно сумме степеней вершин. [1]
Автоморфная эквивалентность [ править ]
Формально: «Две вершины автоморфно эквивалентны, если все вершины можно перемаркировать, чтобы сформировать изоморфный граф с поменянными местами метками u и v. Две автоморфно эквивалентные вершины имеют одни и те же свойства, независимые от метки». [5]
Более интуитивно понятно, что актеры автоморфно эквивалентны, если мы можем переставить граф таким образом, чтобы замена двух актеров не влияла на расстояния между всеми актерами в графе.
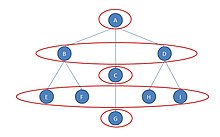
Предположим, что граф описывает организационную структуру компании. Актер A — это центральный офис, актеры B, C и D — менеджеры. Актеры E, F и H, I — работники небольших магазинов; G — одинокий работник в другом магазине.
Хотя актор B и актор D структурно не эквивалентны (у них один и тот же начальник, но не одни и те же работники), они кажутся «эквивалентными» в другом смысле. У обоих менеджеров B и D есть начальник (в данном случае один и тот же начальник), и у каждого по два работника. Если бы мы поменяли их местами, а также поменяли местами четырех рабочих, все расстояния между всеми участниками сети были бы абсолютно идентичными.
На самом деле существует пять классов автоморфной эквивалентности: {A}, {B, D}, {C}, {E, F, H, I} и {G}. Обратите внимание, что менее строгое определение «эквивалентности» сократило количество классов. [2]
эквивалентность Регулярная
Формально: «Два актора обычно эквивалентны, если они в равной степени связаны с эквивалентными другими». Другими словами, регулярно эквивалентные вершины — это вершины, которые, хотя и не обязательно имеют общих соседей, имеют соседей, которые сами похожи. [5]
Две матери, например, эквивалентны, поскольку каждая из них имеет схожий образец связей с мужем, детьми и т. д. Две матери не имеют связей с одним и тем же мужем или с одними и теми же детьми, поэтому они структурно не эквивалентны. Поскольку у разных матерей может быть разное количество мужей и детей, они не будут автоморфно эквивалентны. Но они схожи, поскольку имеют одинаковые отношения с некоторым членом или членами другого набора акторов (которые сами считаются эквивалентными из-за сходства их связей с членом набора «мать»). [2]
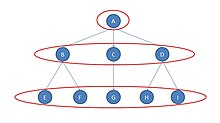
В графе присутствуют три регулярных класса эквивалентности. Первый — актер А; второй состоит из трех актеров B, C и D; третий состоит из оставшихся пяти актеров E, F, G, H и I.
Самый простой класс — это пять действующих лиц в нижней части диаграммы (E, F, G, H и I). Эти актеры регулярно эквивалентны друг другу, потому что:
- они не связаны ни с одним актером первого класса (то есть с актером А) и
- у каждого есть связь с актером второго класса (B, C или D).
Таким образом, каждый из пяти актеров имеет идентичную модель связей с актерами других классов.
Актеры B, C и D аналогичным образом образуют класс. B и D на самом деле имеют связи с двумя членами третьего класса, тогда как актор C имеет связь только с одним членом третьего класса, но это не имеет значения, поскольку существует связь с каким-то членом третьего класса.
Актер A сам по себе находится в классе, определяемом следующим образом:
- связь хотя бы с одним членом второго класса и
- никакой связи ни с одним членом третьего класса. [2]
См. также [ править ]
Ссылки [ править ]
- ↑ Перейти обратно: Перейти обратно: а б с д Ньюман, MEJ 2010. Сети: Введение. Оксфорд, Великобритания: Издательство Оксфордского университета.
- ↑ Перейти обратно: Перейти обратно: а б с д и ж г час Ханнеман, Роберт А. и Марк Риддл. 2005. Введение в методы социальных сетей. Риверсайд, Калифорния: Калифорнийский университет, Риверсайд (опубликовано в цифровой форме по адресу http://faculty.ucr.edu/~hanneman/ )
- ↑ Перейти обратно: Перейти обратно: а б Маркиз, Кристофер; Тилчик, Андраш (01 октября 2016 г.). «Институциональная эквивалентность: как коллеги из отрасли и сообщества влияют на корпоративную благотворительность». Организационная наука . 27 (5): 1325–1341. дои : 10.1287/orsc.2016.1083 . hdl : 1813/44734 . ISSN 1047-7039 .
- ^ Солтон Г., Автоматическая обработка текста: преобразование, анализ и поиск информации с помощью компьютера, Аддисон-Уэсли, Ридинг, Массачусетс (1989).
- ↑ Перейти обратно: Перейти обратно: а б Боргатти, Стивен, Мартин Эверетт и Линтон Фриман. 1992. Руководство пользователя UCINET IV версии 1.0. Колумбия, Южная Каролина: Аналитические технологии.
