Арифметическая иерархия

В математической логике арифметическая иерархия , арифметическая иерархия или иерархия Клини-Мостовского (в честь математиков Стивена Коула Клини и Анджея Мостовского ) классифицирует определенные множества на основе сложности формул , которые их определяют . Любое множество, получающее классификацию, называется арифметическим . Арифметическая иерархия была изобретена независимо Клини (1943) и Мостовским (1946). ^[1]

Арифметическая иерархия важна в теории вычислимости , эффективной описательной теории множеств и изучении формальных теорий, таких как арифметика Пеано .

Алгоритм Тарского-Куратовского обеспечивает простой способ получить верхнюю границу классификаций, присвоенных формуле и множеству, которое она определяет.

Гиперарифметическая иерархия и аналитическая иерархия расширяют арифметическую иерархию для классификации дополнительных формул и наборов.

Арифметическая иерархия формул [ править ]

Арифметическая иерархия присваивает формулам классификации языка арифметики первого порядка . Классификации обозначаются $\Sigma _{n}^{0}$ и $\Pi _{n}^{0}$ для натуральных чисел n (включая 0). Греческие буквы здесь являются светлыми символами, что указывает на то, что формулы не содержат заданных параметров.

Если формула $\phi$ формуле логически эквивалентна , не имеющей неограниченных кванторов, т. е. в которой все кванторы являются ограниченными кванторами, тогда $\phi$ присвоены классификации $\Sigma _{0}^{0}$ и $\Pi _{0}^{0}$ .

Классификации $\Sigma _{n}^{0}$ и $\Pi _{n}^{0}$ определяются индуктивно для каждого натурального числа n по следующим правилам:

Если $\phi$ логически эквивалентна формуле вида $\exists m_{1}\exists m_{2}\cdots \exists m_{k}\psi$ , где $\psi$ является $\Pi _{n}^{0}$ , затем $\phi$ присвоена классификация $\Sigma _{n+1}^{0}$ .
Если $\phi$ логически эквивалентна формуле вида $\forall m_{1}\forall m_{2}\cdots \forall m_{k}\psi$ , где $\psi$ является $\Sigma _{n}^{0}$ , затем $\phi$ присвоена классификация $\Pi _{n+1}^{0}$ .

А $\Sigma _{n}^{0}$ формула эквивалентна формуле, которая начинается с некоторых кванторов существования и их альтернатив. $n-1$ времена между сериями кванторов существования и всеобщности ; в то время как $\Pi _{n}^{0}$ Формула эквивалентна формуле, которая начинается с некоторых кванторов универсальности и чередуется аналогичным образом.

Поскольку каждая формула первого порядка имеет предварительную нормальную форму , каждой формуле присваивается хотя бы одна классификация. Поскольку к любой формуле можно добавить избыточные квантификаторы, как только формуле присвоена классификация $\Sigma _{n}^{0}$ или $\Pi _{n}^{0}$ ему будут присвоены классификации $\Sigma _{m}^{0}$ и $\Pi _{m}^{0}$ для каждого m > n . Таким образом, единственной соответствующей классификацией, присвоенной формуле, является класс с наименьшим n ; все остальные классификации могут быть определены из него.

Значение обозначений [ править ]

Обозначениям арифметической иерархии формул можно придать следующие значения.

Нижний индекс $n$ в символах $\Sigma _{n}^{0}$ и $\Pi _{n}^{0}$ указывает на количество чередований блоков всеобщих и экзистенциальных кванторов первого порядка, используемых в формуле. Более того, самый внешний блок экзистенциален в $\Sigma _{n}^{0}$ формулы и универсальные в $\Pi _{n}^{0}$ формулы.

Надстрочный индекс $0$ в символах $\Sigma _{n}^{0}$ , $\Pi _{n}^{0}$ , и $\Delta _{n}^{0}$ указывает тип объектов, подлежащих количественной оценке. Объекты типа 0 представляют собой натуральные числа, а объекты типа $i+1$ — это функции, которые отображают набор объектов типа $i$ к натуральным числам. Количественная оценка объектов более высокого типа, таких как функции от натуральных чисел до натуральных чисел, описывается верхним индексом больше 0, как в аналитической иерархии . Верхний индекс 0 указывает на квантификаторы чисел, верхний индекс 1 будет указывать на количественный анализ функций от чисел к числам (объекты типа 1), верхний индекс 2 будет соответствовать количественному анализу функций, которые принимают объект типа 1 и возвращают число, и так далее.

Примеры [ править ]

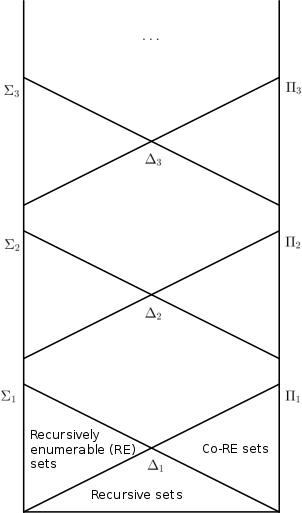
The $\Sigma _{1}^{0}$ множества чисел - это те, которые можно определить по формуле вида $\exists n_{1}\cdots \exists n_{k}\psi (n_{1},\ldots ,n_{k},m)$ где $\psi$ имеет только ограниченные кванторы. Это именно рекурсивно перечислимые множества .
Набор натуральных чисел, которые являются индексами для машин Тьюринга , вычисляющих полные функции, равен $\Pi _{2}^{0}$ . Интуитивно, индекс $e$ попадает в это множество тогда и только тогда, когда для каждого $m$ "есть $s$ такая, что машина Тьюринга с индексом $e$ останавливается на вводе $m$ после $s$ Полное доказательство показало бы, что свойство, заключенное в кавычки в предыдущем предложении, можно определить на языке арифметики Пеано с помощью $\Sigma _{1}^{0}$ формула.
Каждый $\Sigma _{1}^{0}$ подмножество пространства Бэра или пространства Кантора является открытым множеством в обычной топологии пространства. Более того, для любого такого множества существует вычислимая нумерация гёделевых чисел базисных открытых множеств, объединение которых является исходным множеством. По этой причине, $\Sigma _{1}^{0}$ множества иногда называют эффективно открытыми . Аналогично, каждый $\Pi _{1}^{0}$ набор закрыт и $\Pi _{1}^{0}$ множества иногда называют эффективно закрытыми .
Каждое арифметическое подмножество пространства Кантора или пространства Бэра является борелевским множеством . с легкой гранью Иерархия Бореля расширяет арифметическую иерархию, включив в нее дополнительные множества Бореля. Например, каждый $\Pi _{2}^{0}$ подмножество пространства Кантора или Бэра представляет собой $G_{\delta }$ set , то есть набор, равный пересечению счетного числа открытых множеств. Более того, каждое из этих открытых множеств $\Sigma _{1}^{0}$ и список гёделевских чисел этих открытых множеств имеет вычислимую нумерацию. Если $\phi (X,n,m)$ это $\Sigma _{0}^{0}$ формула со свободной заданной переменной $X$ и свободные числовые переменные $n,m$ тогда $\Pi _{2}^{0}$ набор $\{X\mid \forall n\exists m\phi (X,n,m)\}$ является пересечением $\Sigma _{1}^{0}$ наборы формы $\{X\mid \exists m\phi (X,n,m)\}$ как $n$ колеблется по множеству натуральных чисел.
The $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$ формулы можно проверить, просматривая все случаи один за другим, что возможно, поскольку все их кванторы ограничены. Время для этого полиномиально по своим аргументам (например, полиномиально по $n$ для $\varphi (n)$ ); таким образом, соответствующие им проблемы принятия решений включены в E (как $n$ экспоненциально по числу битов). Это больше не соответствует альтернативным определениям $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$ которые позволяют использовать примитивно-рекурсивные функции , поскольку теперь кванторы могут быть связаны любой примитивно-рекурсивной функцией аргументов.
The $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$ формулы в альтернативном определении, позволяющем использовать примитивно-рекурсивные функции с ограниченными кванторами, соответствуют наборам натуральных чисел вида $\{n:f(n)=0\}$ для примитивно-рекурсивной функции $f$ . Это связано с тем, что разрешение ограниченного квантора ничего не добавляет к определению: для примитивно-рекурсивного $f$ , $\forall k<n:f(k)=0$ то же самое, что $f(0)+f(1)+...f(n)=0$ , и $\exists k<n:f(k)=0$ то же самое, что $f(0)\cdot f(1)\cdot \ldots \cdot f(n)=0$ ; с помощью рекурсии курса значений каждый из них может быть определен одной примитивной рекурсивной функцией.

Арифметическая иерархия множеств натуральных чисел [ править ]

Множество X натуральных чисел определяется формулой φ на языке арифметики Пеано (язык первого порядка с символами «0» для нуля, «S» для функции-преемника, «+» для сложения, «×» для умножение и «=" для равенства), если элементы X — это в точности числа, удовлетворяющие φ . То есть для всех натуральных n чисел

n\in X\Leftrightarrow \mathbb {N} \models \varphi ({\underline {n}}),

где ${\underline {n}}$ — числительное на языке арифметики, соответствующее $n$ . Множество определимо в арифметике первого порядка, если оно определяется некоторой формулой языка арифметики Пеано.

Каждому множеству X натуральных чисел, определяемому в арифметике первого порядка, присваиваются классификации вида $\Sigma _{n}^{0}$ , $\Pi _{n}^{0}$ , и $\Delta _{n}^{0}$ , где $n$ является натуральным числом следующим образом. Если X определимо $\Sigma _{n}^{0}$ формула, то X присваивается классификация $\Sigma _{n}^{0}$ . Если X определимо $\Pi _{n}^{0}$ формула, то X присваивается классификация $\Pi _{n}^{0}$ . Если X оба $\Sigma _{n}^{0}$ и $\Pi _{n}^{0}$ затем $X$ присвоена дополнительная классификация $\Delta _{n}^{0}$ .

Обратите внимание, что редко имеет смысл говорить о $\Delta _{n}^{0}$ формулы; первый квантор формулы является либо экзистенциальным, либо универсальным. Итак, $\Delta _{n}^{0}$ множество не обязательно определяется $\Delta _{n}^{0}$ формула в смысле формулы, которая является одновременно $\Sigma _{n}^{0}$ и $\Pi _{n}^{0}$ ; скорее, есть оба $\Sigma _{n}^{0}$ и $\Pi _{n}^{0}$ формулы, определяющие множество. Например, набор нечетных натуральных чисел $n$ определяется либо $\forall k(n\neq 2\times k)$ или $\exists k(n=2\times k+1)$ .

Параллельное определение используется для определения арифметической иерархии конечных декартовых степеней множества натуральных чисел. Вместо формул с одной свободной переменной формулы с k используются для определения арифметической иерархии на множествах из k - наборов натуральных чисел свободными переменными первого порядка. На самом деле они связаны с помощью функции сопряжения .

иерархии Релятивизированные арифметические

Точно так же, как мы можем определить, что означает, что набор X является рекурсивным относительно другого набора Y , позволяя вычислениям, определяющим X , обращаться к Y как к оракулу, мы можем распространить это понятие на всю арифметическую иерархию и определить, что означает X для быть $\Sigma _{n}^{0}$ , $\Delta _{n}^{0}$ или $\Pi _{n}^{0}$ в Y , обозначенный соответственно $\Sigma _{n}^{0,Y}$ , $\Delta _{n}^{0,Y}$ и $\Pi _{n}^{0,Y}$ . Для этого зафиксируем набор натуральных чисел Y и добавим предикат принадлежности Y к языку арифметики Пеано. Тогда мы говорим, что X находится в $\Sigma _{n}^{0,Y}$ если оно определяется $\Sigma _{n}^{0}$ формула на этом расширенном языке. Другими словами, X — это $\Sigma _{n}^{0,Y}$ если оно определяется $\Sigma _{n}^{0}$ формула позволяла задавать вопросы о членстве Y . Альтернативно можно просмотреть $\Sigma _{n}^{0,Y}$ множества — это те множества, которые можно построить, начиная с множеств, рекурсивных по Y, и поочередно объединяя и пересекая эти множества до n раз.

Например, пусть Y — набор натуральных чисел. Пусть X — множество чисел, делящихся на элемент Y . Тогда X определяется по формуле $\phi (n)=\exists m\exists t(Y(m)\land m\times t=n)$ так что X находится внутри $\Sigma _{1}^{0,Y}$ (на самом деле это в $\Delta _{0}^{0,Y}$ также, поскольку мы могли бы ограничить оба квантора числом n ).

и степени сводимость Арифметическая

Арифметическая сводимость — это промежуточное понятие между сводимостью по Тьюрингу и гиперарифметической сводимостью .

Множество является арифметическим (также арифметическим и арифметически определимым ), если оно определяется некоторой формулой на языке арифметики Пеано. Эквивалентно X является арифметическим, X если $\Sigma _{n}^{0}$ или $\Pi _{n}^{0}$ для некоторого натурального числа n . Множество X является арифметическим в множестве Y , обозначаемом $X\leq _{A}Y$ , если X можно определить как некоторую формулу языка арифметики Пеано, расширенную предикатом принадлежности Y . Эквивалентно, X является арифметическим в Y , если X находится в $\Sigma _{n}^{0,Y}$ или $\Pi _{n}^{0,Y}$ для некоторого натурального числа n . Синоним слова $X\leq _{A}Y$ есть: X сводится арифметически к Y .

Отношение $X\leq _{A}Y$ рефлексивно , и, следовательно , и транзитивно отношение $\equiv _{A}$ определяется правилом

X\equiv _{A}Y\iff X\leq _{A}Y\land Y\leq _{A}X

является отношением эквивалентности . Классы эквивалентности этого отношения называются арифметическими степенями ; они частично заказаны под $\leq _{A}$ .

иерархия подмножеств пространства Кантора Арифметическая и Бэра

Канторово пространство , обозначаемое $2^{\omega }$ , — набор всех бесконечных последовательностей нулей и единиц; пространство Бэра , обозначаемое $\omega ^{\omega }$ или ${\mathcal {N}}$ , — множество всех бесконечных последовательностей натуральных чисел. Обратите внимание, что элементы пространства Кантора можно отождествлять с множествами натуральных чисел, а элементы пространства Бэра - с функциями от натуральных чисел к натуральным числам.

Обычная аксиоматизация арифметики второго порядка использует язык, основанный на множествах, в котором кванторы множеств естественным образом можно рассматривать как количественные в канторовом пространстве. Подмножеству канторова пространства присвоена классификация $\Sigma _{n}^{0}$ если оно определяется $\Sigma _{n}^{0}$ формула. Набору присвоена классификация $\Pi _{n}^{0}$ если оно определяется $\Pi _{n}^{0}$ формула. Если набор состоит из обоих $\Sigma _{n}^{0}$ и $\Pi _{n}^{0}$ то ему дается дополнительная классификация $\Delta _{n}^{0}$ . Например, пусть $O\subseteq 2^{\omega }$ быть набором всех бесконечных двоичных строк, которые не все равны 0 (или, что то же самое, набором всех непустых наборов натуральных чисел). Как $O=\{X\in 2^{\omega }|\exists n(X(n)=1)\}$ мы видим это $O$ определяется $\Sigma _{1}^{0}$ формула и, следовательно, является $\Sigma _{1}^{0}$ набор.

Обратите внимание, что хотя и элементы пространства Кантора (рассматриваемые как наборы натуральных чисел), и подмножества пространства Кантора классифицируются в арифметических иерархиях, это не одна и та же иерархия. На самом деле отношения между двумя иерархиями интересны и нетривиальны. Например, $\Pi _{n}^{0}$ элементы канторового пространства (вообще) не совпадают с элементами $X$ пространства Кантора так, что $\{X\}$ это $\Pi _{n}^{0}$ подмножество канторова пространства. Однако многие интересные результаты связывают эти две иерархии.

Есть два способа классифицировать подмножество пространства Бэра в арифметической иерархии.

Подмножество пространства Бэра имеет соответствующее подмножество пространства Кантора под отображением, которое берет каждую функцию из $\omega$ к $\omega$ к характеристической функции ее графика. Подмножеству пространства Бэра присвоена классификация $\Sigma _{n}^{0}$ , $\Pi _{n}^{0}$ , или $\Delta _{n}^{0}$ тогда и только тогда, когда соответствующее подмножество канторова пространства имеет ту же классификацию.
Эквивалентное определение арифметической иерархии в пространстве Бэра дается путем определения арифметической иерархии формул с использованием функциональной версии арифметики второго порядка; тогда арифметическая иерархия подмножеств канторового пространства может быть определена из иерархии пространства Бэра. Это альтернативное определение дает точно такую же классификацию, что и первое определение.

Параллельное определение используется для определения арифметической иерархии конечных декартовых степеней пространства Бэра или пространства Кантора с использованием формул с несколькими свободными переменными. Арифметическая иерархия может быть определена на любом эффективном польском пространстве ; определение особенно просто для пространства Кантора и пространства Бэра, поскольку они соответствуют языку обычной арифметики второго порядка.

Обратите внимание, что мы также можем определить арифметическую иерархию подмножеств пространств Кантора и Бэра относительно некоторого набора натуральных чисел. На самом деле жирный шрифт $\mathbf {\Sigma } _{n}^{0}$ это просто союз $\Sigma _{n}^{0,Y}$ для всех наборов натуральных чисел Y . Обратите внимание, что иерархия, выделенная жирным шрифтом, — это просто стандартная иерархия борелевских множеств .

Расширения и вариации [ править ]

Можно определить арифметическую иерархию формул, используя язык, расширенный символом функции для каждой примитивно-рекурсивной функции . Этот вариант несколько меняет классификацию $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$ , поскольку использование примитивно-рекурсивных функций в арифметике Пеано первого порядка требует, вообще говоря, неограниченного квантора существования и, следовательно, некоторых множеств, которые находятся в $\Sigma _{0}^{0}$ по этому определению находятся строго в $\Sigma _{1}^{0}$ по определению, данному в начале статьи. Класс $\Sigma _{1}^{0}$ и, таким образом, все высшие классы в иерархии остаются незатронутыми.

Более семантический вариант иерархии может быть определен для всех финитных отношений с натуральными числами; используется следующее определение. Каждое вычислимое отношение определяется как $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$ . Классификации $\Sigma _{n}^{0}$ и $\Pi _{n}^{0}$ определяются индуктивно по следующим правилам.

Если отношение $R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})\,$ является $\Sigma _{n}^{0}$ тогда отношение $S(n_{1},\ldots ,n_{l})=\forall m_{1}\cdots \forall m_{k}R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})$ определяется как $\Pi _{n+1}^{0}$
Если отношение $R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})\,$ является $\Pi _{n}^{0}$ тогда отношение $S(n_{1},\ldots ,n_{l})=\exists m_{1}\cdots \exists m_{k}R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})$ определяется как $\Sigma _{n+1}^{0}$

Этот вариант немного меняет классификацию некоторых наборов. В частности, $\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}$ , как класс множеств (определяемый отношениями в классе), идентичен $\Delta _{1}^{0}$ как последний был определен ранее. Его можно расширить, чтобы охватить финитные отношения с натуральными числами, пространством Бэра и пространством Кантора.

Свойства [ править ]

Следующие свойства справедливы для арифметической иерархии множеств натуральных чисел и арифметической иерархии подмножеств пространства Кантора или Бэра.

Коллекции $\Pi _{n}^{0}$ и $\Sigma _{n}^{0}$ замкнуты относительно конечных объединений и конечных пересечений соответствующих элементов.
Набор $\Sigma _{n}^{0}$ тогда и только тогда, когда его дополнение $\Pi _{n}^{0}$ . Набор $\Delta _{n}^{0}$ тогда и только тогда, когда набор является одновременно $\Sigma _{n}^{0}$ и $\Pi _{n}^{0}$ , и в этом случае его дополнение также будет $\Delta _{n}^{0}$ .
Включения $\Pi _{n}^{0}\subsetneq \Pi _{n+1}^{0}$ и $\Sigma _{n}^{0}\subsetneq \Sigma _{n+1}^{0}$ держись за всех $n$ . Таким образом, иерархия не рушится. Это прямое следствие теоремы Поста .
Включения $\Delta _{n}^{0}\subsetneq \Pi _{n}^{0}$ , $\Delta _{n}^{0}\subsetneq \Sigma _{n}^{0}$ и $\Sigma _{n}^{0}\cup \Pi _{n}^{0}\subsetneq \Delta _{n+1}^{0}$ держись за $n\geq 1$ .

Например, для универсальной машины Тьюринга T набор пар ( n , m ), таких что T останавливается на n, но не на m , находится в $\Delta _{2}^{0}$ (будучи вычислимым с помощью оракула проблемы остановки), но не в $\Sigma _{1}^{0}\cup \Pi _{1}^{0}$ .
$\Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}=\Sigma _{0}^{0}\cup \Pi _{0}^{0}\subseteq \Delta _{1}^{0}$ . Включение является строгим по определению, данному в этой статье, но тождество с $\Delta _{1}^{0}$ справедливо при одном из вариантов определения, данного выше .

с Тьюринга Связь машинами

Вычислимые множества [ править ]

Если S — вычислимое по Тьюрингу множество , то и S , и его дополнение рекурсивно перечислимы (если T — машина Тьюринга, дающая 1 для входных данных в S и 0, в противном случае мы можем построить машину Тьюринга, останавливающуюся только на первом, и другую, останавливающуюся только на первом). о последнем).

По теореме Поста и S , и его дополнение находятся в $\Sigma _{1}^{0}$ . Это означает, что S одновременно находится в $\Sigma _{1}^{0}$ и в $\Pi _{1}^{0}$ , и, следовательно, он находится в $\Delta _{1}^{0}$ .

Аналогично, для каждого множества S в $\Delta _{1}^{0}$ , и S , и его дополнение находятся в $\Sigma _{1}^{0}$ и поэтому (по теореме Поста ) рекурсивно перечислимы некоторыми машинами Тьюринга T ₁ и T ₂ соответственно. Для каждого числа n ровно одна из этих остановок. Таким образом, мы можем построить машину Тьюринга T, которая попеременно переключается между T ₁ и T ₂ , останавливаясь и возвращая 1, когда первая останавливается, или останавливаясь и возвращая 0, когда последняя останавливается. Таким образом, T останавливается на каждом n и возвращает значение, находится ли оно в S ; поэтому S вычислимо.

основных Краткое изложение результатов

Вычислимые по Тьюрингу множества натуральных чисел — это в точности множества на уровне $\Delta _{1}^{0}$ арифметической иерархии. Рекурсивно перечислимые множества — это в точности множества на уровне $\Sigma _{1}^{0}$ .

Ни одна машина-оракул не способна решить собственную проблему остановки (применяется вариант доказательства Тьюринга). Проблема остановки для $\Delta _{n}^{0,Y}$ оракул на самом деле сидит в $\Sigma _{n+1}^{0,Y}$ .

Теорема Поста устанавливает тесную связь между арифметической иерархией множеств натуральных чисел и степенями Тьюринга . установлены следующие факты В частности, для всех n ≥ 1 :

Набор $\emptyset ^{(n)}$ ( n- й прыжок Тьюринга пустого множества) является полным в $\Sigma _{n}^{0}$ .
Набор $\mathbb {N} \setminus \emptyset ^{(n)}$ много-один полный в $\Pi _{n}^{0}$ .
Набор $\emptyset ^{(n-1)}$ является ли Тьюринг полным в $\Delta _{n}^{0}$ .

Полиномиальная иерархия - это «возможная, ограниченная ресурсами» версия арифметической иерархии, в которой на задействованные числа накладываются полиномиальные границы длины (или, что то же самое, на задействованные машины Тьюринга накладываются полиномиальные границы времени). Он дает более точную классификацию некоторых наборов натуральных чисел, находящихся на уровне $\Delta _{1}^{0}$ арифметической иерархии.

Связь с другими иерархиями [ править ]

Светлое лицо		Жирный шрифт
С ⁰ ₀ = П ⁰ ₀ = Д ⁰ ₀ (иногда то же, что ∆ ⁰ ₁)		С ⁰ ₀ = П ⁰ ₀ = Д ⁰ ₀ (если определено)
Д ⁰ ₁ = рекурсивный		Д ⁰ ₁ = закрыто открыто
С ⁰ ₁ = рекурсивно перечисляемый	П ⁰ ₁ = корекурсивно перечисляемый	С ⁰ ₁ = G = открыто	П ⁰ ₁ = F = закрыто
Д ⁰ ₂		Д ⁰ ₂
С ⁰ ₂	П ⁰ ₂	С ⁰ ₂ = Ф _п	П ⁰ ₂ = г _δ
Д ⁰ ₃		Д ⁰ ₃
С ⁰ ₃	П ⁰ ₃	С ⁰ ₃ = г _дс	П ⁰ ₃ = Ф _сд
⋮		⋮
С ⁰ _<ω = Р ⁰ _<ω = D ⁰ _<ω = S ¹ ₀ = П ¹ ₀ = Д ¹ ₀ = арифметический		С ⁰ _<ω = Р ⁰ _<ω = D ⁰ _<ω = S ¹ ₀ = П ¹ ₀ = Д ¹ ₀ = жирный арифметический шрифт
⋮		⋮
Д ⁰ _а ( рекурсивный )		Д ⁰ _а ( счетное )
С ⁰ _а	П ⁰ _а	С ⁰ _а	П ⁰ _а
⋮		⋮
С ⁰ _{ой ^СК ₁} = П ⁰ _{ой ^СК ₁} = Д ⁰ _{ой ^СК ₁} = Д ¹ ₁ = гиперарифметический		С ⁰ _{ω ₁} = Р ⁰ _{ω ₁} = Д ⁰ _{ω ₁} = Д ¹ ₁ = Б = Борель
С ¹ ₁ = аналитика светлого лица	П ¹ ₁ = коаналитик светлой поверхности	С ¹ ₁ = А = аналитический	П ¹ ₁ = СА = коаналитический
Д ¹ ₂		Д ¹ ₂
С ¹ ₂	П ¹ ₂	С ¹ ₂ = PCA	П ¹ ₂ = КПКА
Д ¹ ₃		Д ¹ ₃
С ¹ ₃	П ¹ ₃	С ¹ ₃ = ПКПККА	П ¹ ₃ = CPCPCA
⋮		⋮
С ¹ _<ω = Р ¹ _<ω = D ¹ _<ω = S ² ₀ = П ² ₀ = Д ² ₀ = аналитический		С ¹ _<ω = Р ¹ _<ω = D ¹ _<ω = S ² ₀ = П ² ₀ = Д ² ₀ = P = проективный
⋮		⋮

См. также [ править ]

Ссылки [ править ]

^ П. Г. Хинман, Теоретико-рекурсивные иерархии (стр. 89), Перспективы логики, 1978. Springer-Verlag Berlin Heidelberg, ISBN 3-540-07904-1.

Джапаридзе, Георгий (1994), «Логика арифметической иерархии», Анналы чистой и прикладной логики , 66 (2): 89–112, doi : 10.1016/0168-0072(94)90063-9 , Zbl 0804.03045 .
Мошовакис, Яннис Н. (1980), Описательная теория множеств , Исследования по логике и основам математики, том. 100, Северная Голландия, ISBN 0-444-70199-0 , Збл 0433.03025 .
Нис, Андре (2009), Вычислимость и случайность , Oxford Logic Guides, vol. 51, Оксфорд: Издательство Оксфордского университета, ISBN 978-0-19-923076-1 , Збл 1169.03034 .
Роджерс, Х. младший (1967), Теория рекурсивных функций и эффективная вычислимость , Мейденхед: McGraw-Hill, Zbl 0183.01401 .

[1] П. Г. Хинман, Теоретико-рекурсивные иерархии (стр. 89), Перспективы логики, 1978. Springer-Verlag Berlin Heidelberg, ISBN 3-540-07904-1.

[1]

v т и Классы сложности
Считается возможным	ДЛОГТАЙМ переменного тока ⁰ АСС ⁰ ТК ⁰ л СЛ РЛ Флорида Нидерланды NL-полный Северная Каролина СК СС П P-полный ЗПП РП БПП Министерство национальной обороны АПХ ФП
Подозрение неосуществимое	ВВЕРХ НАПРИМЕР NP-полный NP-жесткий со-НП со-NP-полный ТФНП ФНП ЯВЛЯЮСЬ КМА PH ⊕P ПП #П #P-полное ИП PSPACE PSPACE-полный
Считается невозможным	ВРЕМЯ ЭКСПРЕСС СЛЕДУЮЩЕЕ ВРЕМЯ EXPSPACE 2-ВРЕМЯ ЭКСПЛУАТАЦИИ ЭЛЕМЕНТАРНЫЙ пиар Р РЭ ВСЕ
Иерархии классов	Полиномиальная иерархия Экспоненциальная иерархия Иерарх Гжегорчик Арифметическая иерархия Логическая иерархия
Семьи классов	DTIME NTIME ДСПЕЙС НСПАСЕ Вероятностно проверяемое доказательство Интерактивная система доказательств
Список классов сложности