Модель ядерной оболочки
| Ядерная физика |
|---|
 |
В ядерной физике , атомной физике и ядерной химии модель ядерной оболочки использует принцип исключения Паули для моделирования структуры атомных ядер с точки зрения энергетических уровней. [1] Первая модель оболочки была предложена Дмитрием Иваненко (совместно с Э. Гапоном) в 1932 году. Модель была разработана в 1949 году после независимых работ нескольких физиков, в первую очередь Марии Гепперт Майер и Й. Ханса Д. Йенсена , получивших Нобелевскую премию 1963 года. премию по физике за вклад в эту модель, а также Юджина Вигнера , который вместе с ними получил Нобелевскую премию за свои ранние основополагающие работы по атомным ядрам. [2]
Модель ядерной оболочки частично аналогична модели атомной оболочки , которая описывает расположение электронов в атоме, поскольку заполненная оболочка обеспечивает лучшую стабильность. При добавлении нуклонов ( протонов и нейтронов ) к ядру существуют определенные точки, в которых энергия связи следующего нуклона значительно меньше, чем у последнего. Это наблюдение о том, что существуют определенные магические квантовые числа нуклонов ( 2, 8, 20, 28, 50, 82 и 126 ), которые связаны более тесно, чем следующее более высокое число, является источником модели оболочки.
Оболочки протонов и нейтронов независимы друг от друга. Следовательно, могут существовать как «магические ядра», в которых тот или иной тип нуклонов имеют магическое число, так и « дважды магические квантовые ядра », где присутствуют оба типа. Из-за различий в заполнении орбит верхние магические числа составляют 126 и, предположительно, 184 для нейтронов, но только 114 для протонов, играя роль в поисках так называемого острова стабильности . Были найдены некоторые полумагические числа, в частности Z = 40 , которое дает заполнение ядерной оболочки для различных элементов; 16 также может быть магическим числом. [3]
Чтобы получить эти числа, модель ядерной оболочки начинается со среднего потенциала, имеющего форму где-то между квадратной ямой и гармоническим осциллятором . К этому потенциалу добавляется спин-орбитальный член. Но даже в этом случае полное возмущение не совпадает с экспериментом, и к эмпирической спин-орбитальной связи необходимо добавить по крайней мере два или три различных значения ее константы связи, в зависимости от изучаемых ядер.
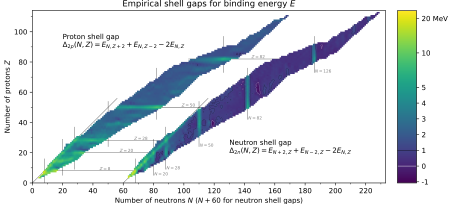
Магические числа ядер, а также другие свойства могут быть получены путем аппроксимации модели трехмерным гармоническим осциллятором плюс спин-орбитальное взаимодействие . Более реалистичный, но сложный потенциал известен как потенциал Вудса-Саксона .
осциллятора Модифицированная модель гармонического
Рассмотрим трехмерный гармонический осциллятор . Это дало бы, например, на первых трёх уровнях (« ℓ » — квантовое число углового момента ):
| уровень n | ℓ | м ℓ | РС |
|---|---|---|---|
| 0 | 0 | 0 | + 1 ⁄ 2 |
| − 1 ⁄ 2 | |||
| 1 | 1 | +1 | + 1 ⁄ 2 |
| − 1 ⁄ 2 | |||
| 0 | + 1 ⁄ 2 | ||
| − 1 ⁄ 2 | |||
| −1 | + 1 ⁄ 2 | ||
| − 1 ⁄ 2 | |||
| 2 | 0 | 0 | + 1 ⁄ 2 |
| − 1 ⁄ 2 | |||
| 2 | +2 | + 1 ⁄ 2 | |
| − 1 ⁄ 2 | |||
| +1 | + 1 ⁄ 2 | ||
| − 1 ⁄ 2 | |||
| 0 | + 1 ⁄ 2 | ||
| − 1 ⁄ 2 | |||
| −1 | + 1 ⁄ 2 | ||
| − 1 ⁄ 2 | |||
| −2 | + 1 ⁄ 2 | ||
| − 1 ⁄ 2 |
Ядра строятся путем добавления протонов и нейтронов . Они всегда будут заполнять самый нижний доступный уровень: первые два протона заполнят нулевой уровень, следующие шесть протонов заполнят первый уровень и так далее. Как и в случае с электронами в периодической таблице , протоны во внешней оболочке будут относительно слабо связаны с ядром, если в этой оболочке всего несколько протонов, поскольку они находятся дальше всего от центра ядра. Следовательно, ядра с полной внешней протонной оболочкой будут иметь более высокую энергию связи ядра , чем другие ядра с аналогичным общим числом протонов. То же самое справедливо и для нейтронов.
Это означает, что ожидается, что магическими числами будут те, у которых все занятые оболочки заполнены. В соответствии с экспериментом получаем 2 (полный уровень 0) и 8 (полные уровни 0 и 1) для первых двух чисел. Однако полный набор магических чисел получается неправильно. Их можно рассчитать следующим образом:
- В трехмерном гармоническом генераторе полное вырождение состояний на уровне n равно .
- За счет спина вырождение удваивается и составляет .
- Таким образом, магические числа будут для всех целых k . Это дает следующие магические числа: 2, 8, 20, 40, 70, 112, ..., которые согласуются с экспериментом только в первых трех записях. Эти числа в два раза больше тетраэдрических чисел (1, 4, 10, 20, 35, 56, ...) из треугольника Паскаля .
В частности, первые шесть снарядов:
- уровень 0: 2 состояния ( ℓ = 0) = 2.
- уровень 1: 6 состояний ( ℓ = 1) = 6.
- уровень 2: 2 состояния ( ℓ = 0) + 10 состояний ( ℓ = 2) = 12.
- уровень 3: 6 состояний ( ℓ = 1) + 14 состояний ( ℓ = 3) = 20.
- уровень 4: 2 состояния ( ℓ = 0) + 10 состояний ( ℓ = 2) + 18 состояний ( ℓ = 4) = 30.
- уровень 5: 6 состояний ( ℓ = 1) + 14 состояний ( ℓ = 3) + 22 состояния ( ℓ = 5) = 42.
где для каждого ℓ существует 2 ℓ +1 различных значений m l и 2 значения m s , что дает в общей сложности 4 ℓ +2 состояния для каждого конкретного уровня.
Эти числа в два раза превышают значения треугольных чисел из треугольника Паскаля: 1, 3, 6, 10, 15, 21,....
спин- орбитальное Включая взаимодействие
Далее мы включим спин-орбитальное взаимодействие . , мы должны описать систему квантовыми числами j , mj водородоподобном и четностью вместо ℓ , ml ms и Во - первых , как в атоме . Поскольку каждый четный уровень включает только четные значения ℓ , он включает в себя только состояния четной (положительной) четности. Аналогично, каждый нечетный уровень включает в себя только состояния нечетной (отрицательной) четности. Таким образом, мы можем игнорировать паритет при подсчете состояний. Первые шесть оболочек, описываемые новыми квантовыми числами,
- уровень 0 ( n = 0): 2 состояния ( j = 1 ⁄ 2 ). Даже паритет.
- уровень 1 ( n = 1): 2 состояния ( j = 1 ⁄ 2 ) + 4 состояния ( j = 3 ⁄ 2 ) = 6. Нечетная четность.
- уровень 2 ( n = 2): 2 состояния ( j = 1 ⁄ 2 ) + 4 состояния ( j = 3 ⁄ 2 ) + 6 состояний ( j = 5 ⁄ 2 ) = 12. Четность.
- уровень 3 ( n = 3): 2 состояния ( j = 1 ⁄ 2 ) + 4 состояния ( j = 3 ⁄ 2 ) + 6 состояний ( j = 5 ⁄ 2 ) + 8 состояний ( j = 7 ⁄ 2 ) = 20. Нечетная четность.
- уровень 4 ( n = 4): 2 состояния ( j = 1 ⁄ 2 ) + 4 состояния ( j = 3 ⁄ 2 ) + 6 состояний ( j = 5 ⁄ 2 ) + 8 состояний ( j = 7 ⁄ 2 ) + 10 состояний ( j = 9 ⁄ 2 ) = 30. Четность.
- уровень 5 ( n = 5): 2 состояния ( j = 1 ⁄ 2 ) + 4 состояния ( j = 3 ⁄ 2 ) + 6 состояний ( j = 5 ⁄ 2 ) + 8 состояний ( j = 7 ⁄ 2 ) + 10 состояний ( j = 9 ⁄ 2 ) + 12 состояний ( j = 11 ⁄ 2 ) = 42. Нечетная четность.
где для каждого j существует 2 j + 1 различных состояний из разных значений m j .
Из-за спин-орбитального взаимодействия энергии состояний одного уровня, но с разными j, перестанут быть одинаковыми. Это связано с тем, что в исходных квантовых числах, когда параллельно , энергия взаимодействия положительна, и в этом случае j = ℓ + s = ℓ + 1 ⁄ 2 . Когда антипараллелен (т.е. направлено противоположно), энергия взаимодействия отрицательна, и в этом случае j = ℓ - s = ℓ - 1 ⁄ 2 . Более того, сила взаимодействия примерно пропорциональна ℓ .
Например, рассмотрим состояния на уровне 4:
- 10 штатов с j = 9 ⁄ 2 происходят от ℓ = 4 и s параллельно ℓ . Таким образом, они имеют положительную энергию спин-орбитального взаимодействия.
- 8 состояний с j = 7 ⁄ 2 из ℓ = 4 и антипараллельно ℓ произошло . Таким образом, они имеют отрицательную энергию спин-орбитального взаимодействия.
- 6 состояний с j = 5 ⁄ 2 произошло от ℓ = 2 и s параллельно ℓ . Таким образом, они имеют положительную энергию спин-орбитального взаимодействия. Однако его величина вдвое меньше, чем у состояний с j = 9 ⁄ 2 .
- 4 состояния с j = 3 ⁄ 2 из ℓ = 2 и антипараллельно ℓ произошло . Таким образом, они имеют отрицательную энергию спин-орбитального взаимодействия. Однако его величина вдвое меньше, чем в состояниях с j = 7 ⁄ 2 .
- Два состояния с j = 1 ⁄ 2 произошло из ℓ = 0 и, следовательно, имеет нулевую энергию спин-орбитального взаимодействия.
Изменение профиля потенциала [ править ]
гармонического осциллятора Потенциал растет бесконечно по мере того, как расстояние от центра r стремится к бесконечности. Более реалистичный потенциал, такой как потенциал Вудса-Саксона , в этом пределе будет приближаться к константе. Одним из главных последствий является то, что в реальном потенциале средний радиус орбит нуклонов будет больше. Это приводит к сокращению срока в операторе Лапласа оператора Гамильтона . Еще одно главное отличие состоит в том, что орбиты с высокими средними радиусами, например, с высоким n или высоким ℓ , будут иметь более низкую энергию, чем в потенциале гармонического осциллятора. Оба эффекта приводят к снижению энергетических уровней высоких ℓ орбит.
Предсказанные магические числа [ править ]

Вместе со спин-орбитальным взаимодействием и при соответствующих величинах обоих эффектов мы приходим к следующей качественной картине: на всех уровнях энергии высших j -состояний сдвинуты вниз, особенно для высоких n (где j наибольшее ). Это связано как с отрицательной энергией спин-орбитального взаимодействия, так и с уменьшением энергии в результате деформации потенциала к более реалистичному. состояний со второго по величине Энергия j- , напротив, сдвигается вверх в результате первого эффекта и вниз в результате второго эффекта, что приводит к небольшому общему сдвигу. Таким образом, сдвиги энергии высших j -состояний могут приблизить энергию состояний одного уровня к энергии состояний более низкого уровня. Тогда «оболочки» модели оболочки больше не будут идентичны уровням, обозначенным n , и магические числа изменяются.
Затем мы можем предположить, что высшие j- состояния для n = 3 имеют промежуточную энергию между средними энергиями n = 2 и n = 3, и предположить, что высшие j -состояния для больших n (по крайней мере, до n = 7) имеют энергия, близкая к средней энергии n - 1 . Тогда получим следующие ракушки (см. рисунок)
- 1-я оболочка: 2 состояния ( n = 0, j = 1 ⁄ 2 ).
- 2-я оболочка: 6 состояний ( n = 1, j = 1 ⁄ 2 или 3 ⁄ 2 ).
- 3-я оболочка: 12 состояний ( n = 2, j = 1 ⁄ 2 , 3 ⁄ 2 или 5 ⁄ 2 ).
- 4-я оболочка: 8 состояний ( n = 3, j = 7 ⁄ 2 ).
- 5-я оболочка: 22 состояния ( n = 3, j = 1 ⁄ 2 , 3 ⁄ 2 или 5 ⁄ 2 ; п = 4, j = 9 ⁄ 2 ).
- 6-я оболочка: 32 состояния ( n = 4, j = 1 ⁄ 2 , 3 ⁄ 2 , 5 ⁄ 2 или 7 ⁄ 2 ; п = 5, j = 11 ⁄ 2 ).
- 7-я оболочка: 44 состояния ( n = 5, j = 1 ⁄ 2 , 3 ⁄ 2 , 5 ⁄ 2 , 7 ⁄ 2 или 9 ⁄ 2 ; п = 6, j = 13 ⁄ 2 ).
- 8-я оболочка: 58 состояний ( n = 6, j = 1 ⁄ 2 , 3 ⁄ 2 , 5 ⁄ 2 , 7 ⁄ 2 , 9 ⁄ 2 или 11 ⁄ 2 ; п = 7, j = 15 ⁄ 2 ).
и так далее.
Обратите внимание, что количество состояний после 4-й оболочки равно удвоенным треугольным числам плюс два . Спин-орбитальное взаимодействие приводит к тому, что так называемые «уровни-нарушители» падают со следующей более высокой оболочки в структуру предыдущей оболочки. Размеры злоумышленников таковы, что размеры получаемых оболочек сами увеличиваются до следующего более высокого удвоенного треугольного числа от размеров гармонического осциллятора. Например, 1f2p имеет 20 нуклонов, а спин-орбитальное взаимодействие добавляет 1g9/2 (10 нуклонов), что приводит к новой оболочке с 30 нуклонами. 1g2d3s имеет 30 нуклонов, а добавление нарушителя 1h11/2 (12 нуклонов) дает новый размер оболочки 42 и так далее.
Тогда магические числа
- 2
- 8 = 2 + 6
- 20 = 2 + 6 + 12
- 28 = 2 + 6 + 12 + 8
- 50 = 2 + 6 + 12 + 8 + 22
- 82 = 2 + 6 + 12 + 8 + 22 + 32
- 126 = 2 + 6 + 12 + 8 + 22 + 32 + 44
- 184 = 2 + 6 + 12 + 8 + 22 + 32 + 44 + 58
и так далее. Это дает все наблюдаемые магические числа, а также предсказывает новое (так называемый остров стабильности ) со значением 184 (для протонов магическое число 126 пока не наблюдалось, и более сложные теоретические соображения предсказывают магическое число вместо этого будет 114).
Другой способ предсказать магические (и полумагические) числа — это установить идеализированный порядок заполнения (с спин-орбитальным расщеплением, но не перекрывающимися энергетическими уровнями). Для согласованности s разбит на компоненты j = 1/2 и j = -1/2 с 2 и 0 членами соответственно. Подсчет крайнего левого и крайнего правого общего количества в последовательностях, ограниченных /, дает магические и полумагические числа.
- s (2,0)/p(4,2) > 2,2/6,8, поэтому (полу)магические числа 2,2/6,8
- d (6,4): s (2,0)/ f (8,6): p (4,2) > 14,18:20,20/28,34:38,40, т. е. 14,20/28 ,40
- г (10,8): д (6,4): с (2,0)/ ч (12,10): ж (8,6): р (4,2) > 50,58,64,68, 70,70/82,92,100,106,110,112, итак 50,70/82,112
- и (14,12): г (10,8): д (6,4): с (2,0)/ j (16,14): ч (12,10): ж (8,6): п (4,2) > 126,138,148,156,162,166,168,168/184,198,210,220,228,234,238,240, т. е. 126,168/184,240
Крайние правые предсказанные магические числа каждой пары внутри квартетов, разделенных пополам /, представляют собой двойные тетраэдрические числа из треугольника Паскаля: 2, 8, 20, 40, 70, 112, 168, 240 равны 2x 1, 4, 10, 20, 35, 56, 84, 120, ..., а крайние левые члены пар отличаются от крайних правых двойными треугольными числами: 2 − 2 = 0, 8 − 6 = 2, 20 − 14 = 6, 40 − 28 = 12, 70–50 = 20, 112–82 = 30, 168–126 = 42, 240–184 = 56, где 0, 2, 6, 12, 20, 30, 42, 56, ... равны 2 × 0, 1. , 3, 6, 10, 15, 21, 28, ... .
Другие свойства ядер [ править ]
Эта модель также предсказывает или с некоторым успехом объясняет другие свойства ядер, в частности, спин и четность ядер основных состояний , в некоторой степени, их возбужденные ядерные состояния , а также . Брать 17
8 O ( кислород-17 ) в качестве примера: его ядро имеет восемь протонов, заполняющих первые три протонных «оболочки», восемь нейтронов, заполняющих первые три нейтронных «оболочки», и один дополнительный нейтрон. Все протоны в полной протонной оболочке имеют нулевой полный угловой момент , поскольку их угловые моменты компенсируют друг друга. То же самое справедливо и для нейтронов. Все протоны на одном уровне ( n ) имеют одинаковую четность (либо +1, либо −1), а поскольку четность пары частиц является произведением их четностей, четное количество протонов с одного уровня ( n ) будет иметь +1 четность. Таким образом, суммарный момент импульса восьми протонов и первых восьми нейтронов равен нулю, а их суммарная четность равна +1. Это означает, что спин (т.е. угловой момент) ядра, а также его четность полностью определяются спином девятого нейтрона. Он находится в первом (т.е. с наименьшей энергией) состоянии 4-й оболочки, которая является d-оболочкой ( ℓ = 2), и поскольку p = (−1) ℓ , это дает ядру общую четность +1. Эта 4-я d-оболочка имеет j = 5 ⁄ 2 , таким образом, ядро 17
8 O будет иметь положительную четность и полный угловой момент. Ожидается, что 5 ⁄ 2 , что действительно так и есть.
Правила упорядочивания оболочек ядра аналогичны правилам Хунда для атомных оболочек, однако, в отличие от их использования в атомной физике, завершение оболочки не означает достижение следующего n , поэтому модель оболочки не может точно предсказать порядок возбужденных состояний ядер, хотя он очень успешно предсказывает основные состояния. Порядок первых нескольких членов указан следующим образом: 1s, 1p. 3 ⁄ 2 , 1п 1 ⁄ 2 , 1д 5 ⁄ 2 , 2с, 1д 3 ⁄ 2 ... Для получения дополнительных пояснений относительно обозначений обратитесь к статье о термине-символе Рассела-Сондерса .
Для ядер, находящихся дальше от магических квантовых чисел, необходимо добавить предположение, что из-за связи между сильным ядерным взаимодействием и полным угловым моментом протоны или нейтроны с одинаковыми n стремятся образовывать пары с противоположными угловыми моментами. Следовательно, ядро с четным числом протонов и четным числом нейтронов имеет спин 0 и положительную четность. Ядро с четным числом протонов и нечетным числом нейтронов (или наоборот) имеет четность последнего нейтрона (или протона), а спин равен полному угловому моменту этого нейтрона (или протона). Под «последними» мы подразумеваем свойства, исходящие с самого высокого энергетического уровня.
В случае ядра с нечетным числом протонов и нечетным числом нейтронов необходимо учитывать полный угловой момент и четность как последнего нейтрона, так и последнего протона. Четность ядер будет их продуктом, а спин ядер будет одним из возможных результатов суммы их угловых моментов (другими возможными результатами являются возбужденные состояния ядра).
Упорядочение уровней углового момента внутри каждой оболочки происходит в соответствии с описанными выше принципами - за счет спин-орбитального взаимодействия, при этом состояния с высокими угловыми моментами смещают свои энергии вниз из-за деформации потенциала (т.е. перехода от потенциала гармонического осциллятора к более реалистичный вариант). Однако для пар нуклонов часто энергетически выгодно иметь высокий угловой момент, даже если его энергетический уровень для одного нуклона был бы выше. Это связано с связью между угловым моментом и сильным ядерным взаимодействием .
Ядерный магнитный момент нейтронов и протонов частично предсказывается этой простой версией модели оболочки. Магнитный момент рассчитывается через j , ℓ и s «последнего» нуклона, но ядра не находятся в состояниях четко определенных ℓ и s . Кроме того, для нечетных ядер приходится учитывать два «последних» нуклона, как в дейтерии . Следовательно, для ядерного магнитного момента можно получить несколько возможных ответов, по одному для каждого возможного комбинированного состояния ℓ и s , а реальное состояние ядра является суперпозицией их . Таким образом, реальный (измеренный) ядерный магнитный момент находится где-то посередине между возможными ответами.
Электрический диполь ядра всегда равен нулю, поскольку его основное состояние имеет определенную четность. Плотность материи ( ψ 2 , где ψ — волновая функция ) всегда инвариантна относительно четности. Обычно так происходит с атомным электрическим диполем .
Более высокие электрические и магнитные мультипольные моменты не могут быть предсказаны этой простой версией оболочечной модели по причинам, аналогичным тем, которые имеются в случае дейтерия .
Включая остаточные взаимодействия [ править ]

Для ядер, имеющих два или более валентных нуклона (т.е. нуклонов вне замкнутой оболочки), необходимо добавить остаточное двухчастичное взаимодействие. Этот остаточный член происходит от части межнуклонного взаимодействия, не включенной в аппроксимативный средний потенциал. Благодаря этому включению происходит смешивание различных конфигураций оболочек и нарушение энергетического вырождения состояний, соответствующих одной и той же конфигурации. [5] [6]
Эти остаточные взаимодействия учитываются посредством расчетов модели оболочки в усеченном модельном пространстве (или валентном пространстве). Это пространство охватывает основу многочастичных состояний, где активны только одночастичные состояния в модельном пространстве. На этой основе решается уравнение Шредингера с использованием эффективного гамильтониана, специально подходящего для модельного пространства. Этот гамильтониан отличается от гамильтониана свободных нуклонов тем, что, среди прочего, он должен компенсировать исключенные конфигурации. [6]
Можно полностью отказаться от приближения среднего потенциала, расширив модельное пространство до ранее инертного ядра и рассматривая все одночастичные состояния вплоть до усечения модельного пространства как активные. Это формирует основу модели оболочки без ядра , которая является методом ab initio . В таких расчетах необходимо учитывать трехчастичное взаимодействие , чтобы добиться согласия с экспериментом. [7]
потенциал деформированный вращение и Коллективное
В 1953 году были обнаружены первые экспериментальные примеры вращательных полос в ядрах, энергетические уровни которых соответствуют той же схеме энергий J (J + 1), что и во вращающихся молекулах. Квантово-механически невозможно коллективное вращение сферы, поэтому это означало, что форма этих ядер была несферической. В принципе, эти вращательные состояния можно было бы описать как когерентные суперпозиции частично-дырочных возбуждений в базисе, состоящем из одночастичных состояний сферического потенциала. Но на самом деле описание этих состояний таким образом сложно из-за большого количества валентных частиц — и эта трудность была еще большей в 1950-х годах, когда вычислительная мощность была крайне рудиментарной. По этим причинам Оге Бор , Бен Моттельсон и Свен Гёста Нильссон построили модели, в которых потенциал был деформирован в эллипсоидную форму. Первая успешная модель такого типа теперь известна как модель Нильссона . По сути, это модель гармонического осциллятора, описанная в этой статье, но с добавленной анизотропией, поэтому частоты осциллятора вдоль трех декартовых осей не одинаковы. Обычно форма представляет собой вытянутый эллипсоид с осью симметрии z. Поскольку потенциал не является сферически симметричным, одночастичные состояния не являются состояниями с хорошим угловым моментом J. Однако множитель Лагранжа , известный как «запускающий» член, можно добавить к гамильтониану. Обычно вектор угловой частоты ω считается перпендикулярным оси симметрии, хотя можно рассматривать и поворот оси с наклоном. Заполнение одночастичных состояний до уровня Ферми создает состояния, ожидаемый угловой момент которых вдоль оси проворачивания является желаемым значением.
Сопутствующие модели [ править ]
Игал Талми разработал метод получения информации из экспериментальных данных и использования ее для расчета и прогнозирования энергий, которые еще не были измерены. Этот метод успешно использовался многими физиками-ядерщиками и привел к более глубокому пониманию структуры ядра. Разработана теория, хорошо описывающая эти свойства. Это описание легло в основу элегантной и успешной модели взаимодействующего бозона .
Моделью, полученной на основе модели ядерной оболочки, является модель альфа-частиц, разработанная Генри Маргенау , Эдвардом Теллером , Дж. К. Перингом, Т. Х. Скирмом , также иногда называемая моделью Скирма . [8] [9] Заметим, однако, что модель Скирма обычно принимается за модель самого нуклона, как «облака» мезонов (пионов), а не за модель ядра как «облака» альфа-частиц.
См. также [ править ]
- Ядерная структура
- Таблица нуклидов
- Модель капли жидкости
- Изомерный сдвиг
- Модель взаимодействующего бозона
Ссылки [ править ]
- ^ «Оболочечная модель ядра» . Гиперфизика .
- ^ Нобелевские лекции по физике, 1963–1970 гг . Амстердам, Нидерланды: Издательство Elsevier. 1972 год . Проверено 19 мая 2023 г.
- ^ Одзава, А.; Кобаяши, Т.; Сузуки, Т.; Ёсида, К.; Танихата, И. (2000). «Новое магическое число, N = 16, возле линии капель нейтронов». Письма о физических отзывах . 84 (24): 5493–5. Бибкод : 2000PhRvL..84.5493O . doi : 10.1103/PhysRevLett.84.5493 . ПМИД 10990977 . (имеется в виду ядерная капельница )
- ^ Ван, Мэн; Ауди, Г.; Кондев, ФГ; Хуанг, WJ; Наими, С.; Сюй, Син (март 2017 г.). «Оценка атомной массы AME2016 (II). Таблицы, графики и ссылки». Китайская физика C . 41 (3): 030003. Бибкод : 2017ChPhC..41c0003W . дои : 10.1088/1674-1137/41/3/030003 . hdl : 11858/00-001M-0000-0010-23E8-5 . ISSN 1674-1137 .
- ^ Корье, Э.; Мартинес-Пинедо, Г.; Новацкий, Ф.; Повес, А.; Цукер, AP (2005). «Оболочечная модель как единый взгляд на структуру ядра». Обзоры современной физики . 77 (2): 427–488. arXiv : nucl-th/0402046 . Бибкод : 2005РвМП...77..427С . дои : 10.1103/RevModPhys.77.427 . S2CID 119447053 .
- ^ Jump up to: Перейти обратно: а б Кораджо, Л.; Ковелло, А.; Гаргано, А.; Итако, Н.; Куо, ТТС (2009). «Расчеты модели оболочки и реалистичные эффективные взаимодействия». Прогресс в области физики элементарных частиц и ядерной физики . 62 (1): 135–182. arXiv : 0809.2144 . Бибкод : 2009ПрПНП..62..135С . дои : 10.1016/j.ppnp.2008.06.001 . S2CID 18722872 .
- ^ Барретт, БР; Навратил, П.; Вари, JP (2013). «С самого начала нет модели базовой оболочки». Прогресс в области физики элементарных частиц и ядерной физики . 69 : 131–181. arXiv : 0902.3510 . Бибкод : 2013ПрПНП..69..131Б . дои : 10.1016/j.ppnp.2012.10.003 .
- ^ Скирм, THR (7 февраля 1961 г.). «Нелинейная теория поля». Труды Королевского общества A: Математические, физические и технические науки . 260 (1300): 127–138. Бибкод : 1961RSPSA.260..127S . дои : 10.1098/rspa.1961.0018 . S2CID 122604321 .
- ^ Скирм, THR (март 1962 г.). «Единая полевая теория мезонов и барионов». Ядерная физика . 31 : 556–569. Бибкод : 1962NucPh..31..556S . дои : 10.1016/0029-5582(62)90775-7 .
Дальнейшее чтение [ править ]
- Талми, Игал; де-Шалит, А. (1963). Теория ядерных оболочек . АкадемикПресс. ISBN 978-0-486-43933-4 .
- Талми, Игал (1993). Простые модели сложных ядер: модель оболочки и модель взаимодействующего бозона . Академическое издательство Харвуда. ISBN 978-3-7186-0551-4 .
Внешние ссылки [ править ]
- Игал Талми (24 ноября 2010 г.). Об однонуклонных волновых функциях . РИКЕН Нишина Центр.









