Ядерная структура

Понимание структуры атомного ядра является одной из центральных задач ядерной физики .

Модели [ править ]

Кластерная модель [ править ]

Кластерная модель описывает ядро как молекулообразную совокупность протон-нейтронных групп (например, альфа-частиц ) с одним или несколькими валентными нейтронами, занимающими молекулярные орбитали. ^[1]^[2]^[3]^[4]

Модель капли жидкости [ править ]

Модель жидкой капли — одна из первых моделей структуры ядра , предложенная Карлом Фридрихом фон Вайцзеккером в 1935 году. ^[5] Он описывает ядро как квазиклассическую жидкость, состоящую из нейтронов и протонов , с внутренней электростатической силой отталкивания , пропорциональной числу протонов. Квантово -механическая природа этих частиц проявляется в принципе Паули , который гласит, что никакие два нуклона одного и того же вида не могут находиться в одном и том же состоянии . Таким образом, жидкость на самом деле является ферми-жидкостью .В этой модели энергия связи ядра с $Z$ протоны и $N$ нейтронов определяется выражением

E_{B}=a_{V}A-a_{S}A^{2/3}-a_{C}{\frac {Z^{2}}{A^{1/3}}}-a_{A}{\frac {(N-Z)^{2}}{A}}-\delta (A,Z)

где $A=Z+N$ — общее количество нуклонов ( массовое число ). Члены, пропорциональные $A$ и $A^{2/3}$ представляют объем и поверхностную энергию капли жидкости, член пропорционален $Z^{2}$ представляет электростатическую энергию, член пропорционален $(N-Z)^{2}$ представляет принцип исключения Паули и последний член $\delta (A,Z)$ - это спаривающий член, который снижает энергию четного числа протонов или нейтронов.Коэффициенты $a_{V},a_{S},a_{C},a_{A}$ и сила спаривающего члена может быть оценена теоретически или соответствовать данным.Эта простая модель воспроизводит основные особенности энергии связи ядер.

Предположение о ядре как о капле ферми-жидкости до сих пор широко используется в форме модели капель с конечным радиусом действия (FRDM) из-за возможного хорошего воспроизведения энергии связи ядра на всей диаграмме с необходимой точностью для предсказания неизвестных ядер. . ^[6]

Модель оболочки [ править ]

Выражение «модель оболочки» неоднозначно, поскольку оно относится к двум разным объектам. Ранее оно использовалось для описания существования нуклонных оболочек в соответствии с подходом, близким к тому, что сейчас называется теорией среднего поля .В настоящее время это относится к формализму, аналогичному формализму конфигурационного взаимодействия , используемому в квантовой химии .

Введение в концепцию оболочки [ править ]

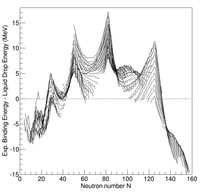
Систематические измерения энергии связи атомных ядер показывают систематические отклонения от оценок, полученных на основе модели жидкой капли. В частности, некоторые ядра, имеющие определенные значения числа протонов и/или нейтронов, связаны между собой более прочно, чем предсказывает модель жидкой капли. Эти ядра называются одинарно/двойно магическими . Это наблюдение привело ученых к предположению о существовании оболочечной структуры нуклонов (протонов и нейтронов) внутри ядра, подобной оболочечной структуре электронов внутри атомов.

Действительно, нуклоны являются квантовыми объектами . Строго говоря, не следует говорить об энергиях отдельных нуклонов, поскольку все они коррелированы друг с другом. Однако в качестве приближения можно представить себе среднее ядро, внутри которого нуклоны распространяются индивидуально. Благодаря своему квантовому характеру они могут занимать только дискретные энергетические уровни . Эти уровни ни в коем случае не распределены равномерно; некоторые интервалы энергии переполнены, а некоторые пусты, создавая разрыв в возможных энергиях. Оболочка — это такой набор уровней, отделенный от остальных широким пустым промежутком.

Уровни энергии находятся путем решения уравнения Шредингера для одного нуклона, движущегося в среднем потенциале, создаваемом всеми остальными нуклонами. Каждый уровень может быть занят нуклоном или пуст. На некоторых уровнях находится несколько разных квантовых состояний с одинаковой энергией; их называют дегенератами . Это происходит, в частности, если среднее ядро демонстрирует определенную симметрию , например, сферическую форму.

Представление об оболочках позволяет понять, почему некоторые ядра связаны более прочно, чем другие. Это связано с тем, что два нуклона одного и того же вида не могут находиться в одном и том же состоянии ( принцип Паули ). Вернер Гейзенберг распространил принцип исключения Паули на нуклоны, введя концепцию изоспина. ^[7] Считается, что нуклоны состоят из двух типов частиц: нейтрона и протона, которые различаются своими внутренними свойствами, связанными с их изо-спиновым квантовым числом. Эта концепция позволяет объяснить связанное состояние дейтерия , в котором протон и нейтрон могут связывать свой спин и изо-спин двумя разными способами. Таким образом, состояние ядра с самой низкой энергией — это состояние, в котором нуклоны заполняют все энергетические уровни от нижнего до некоторого уровня. Ядра с нечетным числом протонов или нейтронов менее связаны, чем ядра с четным числом. Ядро с полной оболочкой исключительно стабильно, как будет объяснено ниже.

Как и в случае с электронами в модели электронной оболочки , протоны во внешней оболочке относительно слабо связаны с ядром, если в этой оболочке всего несколько протонов, поскольку они находятся дальше всего от центра ядра. Следовательно, ядра, имеющие полную внешнюю протонную оболочку, будут более прочно связанными и будут иметь более высокую энергию связи, чем другие ядра с аналогичным общим числом протонов. Это справедливо и для нейтронов.

Более того, энергия, необходимая для возбуждения ядра (т.е. перемещения нуклона на более высокий, ранее незанятый уровень), в таких ядрах исключительно высока. Всякий раз, когда этот незанятый уровень является следующим после полной оболочки, единственный способ возбудить ядро — поднять один нуклон через щель , затрачивая при этом большое количество энергии. В противном случае, если самый высокий занятый энергетический уровень находится в частично заполненной оболочке, для перевода нуклона в более высокое состояние в той же оболочке потребуется гораздо меньше энергии.

Ожидается некоторая эволюция оболочечной структуры, наблюдаемая в стабильных ядрах, вдали от долины стабильности . Например, наблюдения нестабильных изотопов показали смещение и даже переупорядочение одночастичных уровней, из которых состоит оболочечная структура. ^[8] Иногда это наблюдается как создание острова инверсии или уменьшение энергетических разрывов возбуждения сверх традиционных магических чисел.

Основные гипотезы [ править ]

Для того чтобы дать точную концептуальную основу модели оболочки, выдвигаются некоторые основные гипотезы:

Атомное ядро представляет собой квантовую систему из n тел.
Внутреннее движение нуклонов внутри ядра нерелятивистское, и их поведение определяется уравнением Шрёдингера .
Нуклоны считаются точечными, без какой-либо внутренней структуры.

Краткое описание формализма [ править ]

Общий процесс, используемый в расчетах модели оболочки, заключается в следующем. Сначала определяется гамильтониан ядра. Обычно для практичности вычислений в этом определении учитываются только термины одного и двух тел. Взаимодействие является эффективной теорией : оно содержит свободные параметры, которые необходимо согласовать с экспериментальными данными.

Следующий шаг состоит в определении основы одночастичных состояний, т.е. набора волновых функций, описывающих все возможные состояния нуклона. В большинстве случаев этот базис получается с помощью вычислений Хартри – Фока . С помощью этого набора одночастичных состояний определители Слейтера строятся , то есть волновые функции для Z протонных переменных или N нейтронных переменных, которые представляют собой антисимметричные произведения одночастичных волновых функций (антисимметричность означает, что при обмене переменных для любой пары нуклонов волновая функция меняет только знак).

В принципе, число квантовых состояний, доступных для одного нуклона при конечной энергии, конечно, скажем, n . Число нуклонов в ядре должно быть меньше числа доступных состояний, иначе ядро не сможет удерживать все свои нуклоны. Таким образом, существует несколько способов выбора Z (или N ) состояний среди n возможных. В комбинаторной математике количество вариантов выбора Z объектов среди n называется биномиальным коэффициентом C. ^С
_н . Если n намного больше, чем Z (или N ), оно увеличивается примерно как n ^С. На практике это число становится настолько большим, что каждое вычисление становится невозможным для A = N + Z , большего 8.

Чтобы обойти эту трудность, пространство возможных одночастичных состояний разделяется на остовное и валентное по аналогии с химией (см. остовный электрон и валентный электрон ). Ядро представляет собой набор одиночных частиц, которые считаются неактивными в том смысле, что они представляют собой хорошо связанные состояния с наименьшей энергией, и что нет необходимости пересматривать их ситуацию. Они не появляются в детерминантах Слейтера, в отличие от состояний в валентном пространстве, которое представляет собой пространство всех одночастичных состояний, не находящихся в ядре , но, возможно, подлежащих учету при выборе построения ( Z -) N -волновая функция тела. Набор всех возможных определителей Слейтера в валентном пространстве определяет основу для ( Z -) N -состояний тел.

Последний шаг состоит в вычислении матрицы гамильтониана в этом базисе и ее диагонализации. Несмотря на уменьшение размерности базиса за счет фиксации ядра, диагонализуемые матрицы легко достигают размеров порядка 10 ⁹и требуют специальных методов диагонализации.

Расчеты модели оболочки в целом хорошо согласуются с экспериментальными данными. Однако они сильно зависят от двух основных факторов:

Способ разделения одночастичного пространства на ядро и валентность.
Эффективное нуклон-нуклонное взаимодействие.

среднего Теории поля

Модель независимых частиц (IPM) [ править ]

Взаимодействие между нуклонами , которое является следствием сильных взаимодействий и связывает нуклоны внутри ядра, демонстрирует своеобразное поведение, имеющее конечный радиус действия: оно исчезает, когда расстояние между двумя нуклонами становится слишком большим; он привлекателен на средней дистанции и отталкивает на очень малой дистанции. Последнее свойство коррелирует с принципом запрета Паули, согласно которому два фермиона (нуклоны — это фермионы) не могут находиться в одном и том же квантовом состоянии. Это приводит к очень большой средней длине свободного пробега , предсказанной для нуклона внутри ядра. ^[9]

Основная идея подхода независимых частиц заключается в том, что нуклон движется внутри определенной потенциальной ямы (которая удерживает его связанной с ядром) независимо от других нуклонов. Это равнозначно замене задачи N тел ( N взаимодействующих частиц) на N задач одного тела. Это существенное упрощение проблемы является краеугольным камнем теорий среднего поля. Они также широко используются в атомной физике , где электроны движутся в среднем поле благодаря центральному ядру и самому электронному облаку.

Модель независимых частиц и теории среднего поля (мы увидим, что существует несколько вариантов) имеют большой успех в описании свойств ядра, начиная с эффективного взаимодействия или эффективного потенциала, и, таким образом, являются основной частью теории атомного ядра. Следует также отметить, что они достаточно модульны, поскольку довольно легко расширить модель , включив в нее такие эффекты, как спаривание ядер или коллективные движения нуклона, такие как вращение или вибрация , добавив соответствующие энергетические члены в формализм. Это означает, что во многих представлениях среднее поле является лишь отправной точкой для более полного описания, которое вводит корреляции, воспроизводящие такие свойства, как коллективные возбуждения и перенос нуклонов. ^[10]^[11]

потенциал и взаимодействие эффективное Ядерный

Большая часть практических трудностей, встречающихся в теориях среднего поля, связана с определением (или вычислением) потенциала самого среднего поля. Можно очень грубо различать два подхода:

Феноменологический подход представляет собой параметризацию ядерного потенциала соответствующей математической функцией. Исторически эту процедуру с наибольшим успехом применил Свен Гёста Нильссон , который использовал в качестве потенциала (деформированный) потенциал гармонического осциллятора . Самые последние параметризации основаны на более реалистичных функциях, которые более точно учитывают, например, эксперименты по рассеянию. форму, известную как потенциал Вудса–Саксона . В частности, можно упомянуть
подход Самосогласованный или подход Хартри-Фока направлен на математический вывод ядерного потенциала из эффективного нуклон-нуклонного взаимодействия. Этот метод подразумевает решение уравнения Шредингера итеративным способом, начиная с анзац-волновой функции и вариационно улучшая ее, поскольку потенциал здесь зависит от волновых функций, которые необходимо определить. Последние записываются как определители Слейтера .

В случае подходов Хартри–Фока проблема состоит не в том, чтобы найти математическую функцию, которая лучше всего описывает ядерный потенциал, а в том, что лучше всего описывает нуклон-нуклонное взаимодействие. Действительно, в отличие от атомной физики , где взаимодействие известно (это кулоновское взаимодействие), нуклон-нуклонное взаимодействие внутри ядра не известно аналитически.

Этому есть две основные причины. Во-первых, сильное взаимодействие действует преимущественно между кварками, образующими нуклоны. Нуклон -нуклонное взаимодействие в вакууме является лишь следствием кварк-кваркового взаимодействия. Хотя последнее хорошо понимается в рамках Стандартной модели при высоких энергиях, оно гораздо сложнее при низких энергиях из-за ограничения цвета и асимптотической свободы . Таким образом, до сих пор не существует фундаментальной теории, позволяющей вывести нуклон-нуклонное взаимодействие из кварк-кваркового взаимодействия. Более того, даже если бы эта проблема была решена, оставалась бы большая разница между идеальным (и концептуально более простым) случаем двух нуклонов, взаимодействующих в вакууме, и случаем, когда эти нуклоны взаимодействуют в ядерной материи. Чтобы пойти дальше, необходимо было изобрести концепцию эффективного взаимодействия . Последний по сути представляет собой математическую функцию с несколькими произвольными параметрами, которые настраиваются в соответствии с экспериментальными данными.

Большинство современных взаимодействий являются нулевыми, поэтому они действуют только тогда, когда два нуклона находятся в контакте, как это представил Тони Скирм . ^[12] В основополагающей статье ^[13] Доминик Вотерен и Дэвид М. Бринк продемонстрировали, что сила Скирма, зависящая от плотности, может воспроизводить основные свойства атомных ядер. Другое часто используемое взаимодействие - это сила Гогни конечного диапазона, ^[14]

Самосогласованные подходы типа – Фока Хартри

В Хартри-Фока подходе к задаче n тел отправной точкой является гамильтониан, содержащий n членов кинетической энергии и потенциальных членов. Как упоминалось ранее, одна из гипотез теории среднего поля состоит в том, что следует учитывать только взаимодействие двух тел. Потенциальный член гамильтониана представляет все возможные двухчастичные взаимодействия в наборе n фермионов . Это первая гипотеза.

Второй шаг состоит в предположении, что волновую функцию системы можно записать в виде определителя Слейтера одночастичных спин-орбиталей . Это утверждение представляет собой математический перевод модели независимых частиц. Это вторая гипотеза.

Осталось теперь определить компоненты этого определителя Слейтера, т. е. индивидуальные волновые функции нуклонов. Для этого предполагается, что полная волновая функция (определитель Слейтера) такова, что энергия минимальна. Это третья гипотеза.

Технически это означает, что нужно вычислить среднее значение (известного) двухчастичного гамильтониана на (неизвестном) определителе Слейтера и добиться исчезновения его математической вариации . Это приводит к набору уравнений, в которых неизвестными являются отдельные волновые функции: уравнения Хартри – Фока. Решение этих уравнений дает волновые функции и отдельные уровни энергии нуклонов, а значит, полную энергию ядра и его волновую функцию.

Это краткое описание метода Хартри–Фока объясняет, почему его также называют вариационным подходом. В начале расчета полная энергия является «функцией отдельных волновых функций» (так называемый функционал), а затем все делается для того, чтобы оптимизировать выбор этих волновых функций так, чтобы функционал имел минимум – будем надеяться абсолютный, а не только локальный. Точнее, следует упомянуть, что энергия является функционалом плотности , определяемым как сумма отдельных квадратов волновых функций. Метод Хартри-Фока также используется в атомной физике и физике конденсированного состояния как теория функционала плотности, DFT.

Процесс решения уравнений Хартри–Фока может быть только итеративным, поскольку это по сути уравнение Шредингера , в котором потенциал зависит от плотности , то есть именно от волновых функций определяемых . Практически алгоритм начинается с набора отдельных вполне разумных волновых функций (в общем, собственных функций гармонического осциллятора ). Они позволяют рассчитать плотность и, следовательно, потенциал Хартри – Фока. Как только это будет сделано, уравнение Шредингера решается заново и так далее. Расчет прекращается – сходимость достигается – когда разница между волновыми функциями или уровнями энергии для двух последовательных итераций становится меньше фиксированного значения. Тогда средний потенциал поля полностью определяется и уравнения Хартри–Фока становятся стандартными уравнениями Шрёдингера. Соответствующий гамильтониан тогда называется гамильтонианом Хартри – Фока.

Релятивистское приближается поле среднее

модели ядра , зародившиеся впервые в 1970-х годах вместе с работами Джона Дирка Валеки по квантовой адродинамике , Релятивистские были усовершенствованы к концу 1980-х годов П. Рингом и его сотрудниками. Отправной точкой этих подходов является релятивистская квантовая теория поля . В этом контексте взаимодействия нуклонов происходят посредством обмена виртуальными частицами, называемыми мезонами . Идея состоит в том, чтобы на первом этапе построить лагранжиан, содержащий эти члены взаимодействия. Во-вторых, применяя принцип наименьшего действия , можно получить систему уравнений движения. Реальные частицы (здесь нуклоны) подчиняются уравнению Дирака , а виртуальные (здесь мезоны) подчиняются уравнениям Клейна-Гордона .

Ввиду непертурбативной природы сильного взаимодействия, а также того, что точная потенциальная форма этого взаимодействия между группами нуклонов сравнительно плохо известна, использование такого подхода в случае атомных ядер требует радикальных приближений. Основное упрощение состоит в замене в уравнениях всех членов поля (которые являются операторами в математическом смысле ) их средним значением (которые являются функциями ). Таким образом, получается система связанных интегро-дифференциальных уравнений , которую можно решить если не аналитически, то численно.

Модель взаимодействующего бозона

Модель взаимодействующего бозона (IBM) — это модель ядерной физики, в которой нуклоны представлены парами, каждый из которых действует как бозонная частица с интегральным спином 0, 2 или 4. Это делает возможными расчеты для более крупных ядер.Существует несколько ветвей этой модели - в одной из них (ИБМ-1) можно группировать все типы нуклонов попарно, в других (например - ИБМ-2) рассматривать протоны и нейтроны в парах отдельно.

симметрии в ядерной Спонтанное нарушение физике

Одним из основных моментов всей физики является симметрия . Нуклон-нуклонное взаимодействие и все эффективные взаимодействия, используемые на практике, обладают определенной симметрией. Они инвариантны при переносе (изменении системы отсчета так, чтобы направления не менялись), вращении ( повороте системы отсчета вокруг некоторой оси) или четности (изменении направления осей) в том смысле, что взаимодействие не меняется. при любой из этих операций. Тем не менее в подходе Хартри–Фока могут появиться решения, не инвариантные относительно такой симметрии. Тогда говорят о спонтанном нарушении симметрии .

Качественно эти спонтанные нарушения симметрии можно объяснить следующим образом: в теории среднего поля ядро описывается как набор независимых частиц. Большинством дополнительных корреляций между нуклонами, не попадающими в среднее поле, пренебрегают. Однако они могут появиться в результате нарушения симметрии гамильтониана среднего поля, которая является лишь приближенной. Если плотность, используемая для запуска итераций процесса Хартри-Фока, нарушает определенные симметрии, окончательный гамильтониан Хартри-Фока может нарушить эти симметрии, если выгодно сохранять их нарушенными с точки зрения полной энергии.

Он также может сходиться к симметричному решению. В любом случае, если окончательное решение нарушает симметрию, например, вращательную симметрию, так что ядро оказывается не сферическим, а эллиптическим, все конфигурации, выведенные из этого деформированного ядра путем вращения, являются столь же хорошими решениями для уравнения Хартри. – Проблема с Фоком. При этом основное состояние ядра вырождается .

Аналогичное явление происходит и с ядерным спариванием, нарушающим закон сохранения числа барионов (см. ниже).

среднего Расширения теорий поля

Феномен ядерного спаривания

Наиболее распространенным расширением теории среднего поля является спаривание ядер. Ядра с четным числом нуклонов систематически более связаны, чем ядра с нечетным числом. Это означает, что каждый нуклон связывается с другим, образуя пару, следовательно, систему нельзя описать как независимые частицы, находящиеся под действием общего среднего поля. Когда в ядре четное количество протонов и нейтронов, каждый из них находит партнера. Чтобы возбудить такую систему, надо использовать как минимум такую энергию, чтобы разорвать пару. И наоборот, в случае нечетного числа протонов или нейтронов существует неспаренный нуклон, для возбуждения которого требуется меньше энергии.

Это явление очень похоже на явление сверхпроводимости 1-го типа в физике твердого тела. Первое теоретическое описание спаривания ядер было предложено в конце 1950-х годов Оге Бором , Беном Моттельсоном и Дэвидом Пайнсом (что способствовало получению Бором и Моттельсоном Нобелевской премии по физике в 1975 году). ^[15] Она была близка к теории БКШ Бардина, Купера и Шриффера, объясняющей сверхпроводимость металлов. Теоретически явление спаривания, описанное теорией БКШ, сочетается с теорией среднего поля: нуклоны подвержены как потенциалу среднего поля, так и спаривающему взаимодействию.

Метод Хартри-Фока-Боголюбова (HFB) представляет собой более сложный подход. ^[16] позволяющий последовательно и на равных рассматривать спаривание и среднеполевые взаимодействия. В настоящее время HFB является фактическим стандартом при средней полевой обработке ядерных систем.

Восстановление симметрии [ править ]

Особенностью методов среднего поля является расчет ядерных свойств путем явного нарушения симметрии . Расчет среднего поля самосогласованными методами (например, Хартри-Фока) нарушает вращательную симметрию, а расчет свойства спаривания нарушает число частиц.

Было разработано несколько методов восстановления симметрии путем проецирования хороших квантовых чисел. ^[17]

Вибрационная связь частиц [ править ]

Методы среднего поля (в конечном итоге с учетом восстановления симметрии) являются хорошим приближением основного состояния системы, даже постулируя систему независимых частиц. Поправки высшего порядка учитывают тот факт, что частицы взаимодействуют друг с другом посредством корреляции. Эти корреляции могут быть введены с учетом связи независимых степеней свободы частиц, низкоэнергетического коллективного возбуждения систем с четным числом протонов и нейтронов.

Таким образом, возбужденные состояния могут быть воспроизведены с помощью приближения случайной фазы (RPA), а также в конечном итоге последовательно рассчитываются поправки к основному состоянию (например, с помощью теории ядерного поля). ^[11]).

См. также [ править ]

Ядерный магнитный момент
CHARISSA , сотрудничество в области исследования ядерной структуры

Дальнейшее чтение [ править ]

Общая аудитория [ править ]

Джеймс М. Корк; Радиоактивность и ядерная физика , Дюно (1949).

Вводные тексты [ править ]

Люк Валентин; Субатомный мир — От кварков до атомных электростанций , Герман (1986).
Люк Валентин; Ядра и частицы – модели и симметрии , Герман (1997).
Дэвид Холлидей; Введение в ядерную физику , Wiley & Sons (1957).
Кеннет Крейн; Введение в ядерную физику , Wiley & Sons (1987).
Карлос Бертулани; Ядерная физика в двух словах , Издательство Принстонского университета (2007).

Фундаментальные тексты [ править ]

Питер Э. Ходжсон ; Ядерные реакции и структура ядра . Издательство Оксфордского университета (1971).
Ирвинг Каплан; Ядерная физика , серия Аддисона-Уэсли по ядерной науке и технике, Аддисон-Уэсли (1956). 2-е издание (1962 г.).
А. Бор и Б. Моттельсон; Ядерная структура , 2 тома, Бенджамин (1969–1975). Том 1: Движение одиночной частицы ; Том 2: Ядерные деформации . Redité par World Scientific Publishing Company (1998), ISBN 981-02-3197-0 .
П. Ринг и П. Шук; Ядерная проблема многих тел , Springer Verlag (1980), ISBN 3-540-21206-X
А. де Шалит и Х. Фешбах; Теоретическая ядерная физика , 2 тома, John Wiley & Sons (1974). Том 1: Ядерная структура ; Том 2: Ядерные реакции , ISBN 0-471-20385-8

Ссылки [ править ]

^ Эренштейн, Дэвид (21 ноября 2023 г.). «Основное состояние ядра имеет структуру, подобную молекуле» . Проверено 23 ноября 2023 г.
^ Ли, Пэнцзе (2023). «Подтверждение молекулярной структуры основного состояния 10Be с использованием измерений сечения тройной дифференциальной реакции 10Be(p,pα)6He». Письма о физических отзывах . arXiv : 2311.13129 . doi : 10.1103/PhysRevLett.131.212501 .
^ Эбран, JP (2012). «Как кластеризуются атомные ядра». Природа . 487 : 341–344. arXiv : 1203.1244 . дои : 10.1038/nature11246 .
^ Вильдермут, К. (1958). «Кластерная модель» атомных ядер». Ядерная физика . 7 : 150–162. дои : 10.1016/0029-5582(58)90245-1 .
^ фон Вайцзеккер, CF (1935). «К теории ядерных масс». Журнал физики (на немецком языке). 96 (7–8): 431–458. Бибкод : 1935ZPhy...96..431W . дои : 10.1007/BF01337700 . S2CID 118231854 .
^ Мёллер, П.; Майерс, WD; Святецкий, WJ; Трейнер, Дж. (3 сентября 1984 г.). «Модель капли конечного радиуса действия». Конференция: 7. Международная конференция по атомным массам и фундаментальным константам (AMCO-7), Дармштадт-Зеехайм, Франция. Германия . ОСТИ 6441187 .
^ Гейзенберг, В. (1 января 1932 г.). «О строении атомных ядер. I» . Журнал физики (на немецком языке). 77 (1): 1–11. дои : 10.1007/BF01342433 . ISSN 0044-3328 .
^ Сорлин, О.; Порке, М.-Ж. (2008). «Ядерная магия чисел: новые возможности, далекие от стабильности». Прогресс в области физики элементарных частиц и ядерной физики . 61 (2): 602–673. arXiv : 0805.2561 . Бибкод : 2008ПрПНП..61..602С . дои : 10.1016/j.ppnp.2008.05.001 . S2CID 118524326 .
^ Бринк, Дэвид; Бролья, Рикардо А. (2005). Ядерная сверхтекучесть . Издательство Кембриджского университета. ISBN 9781139443074 .
^ Кольцо, П.; Шук, П. (1980). Ядерная проблема многих тел . Спрингер Верлаг. ISBN 978-3-540-21206-5 .
↑ Перейти обратно: Перейти обратно: ^а ^б Идини, А.; Потель, Г.; Барранко, Ф.; Вигецци, Э.; Бролья, РА (2015). «Переплетение элементарных мод возбуждения в сверхтекучих ядрах посредством взаимодействия частиц и колебаний: количественный учет разнообразия наблюдаемых структур ядра». Физический обзор C . 92 (3): 031304. arXiv : 1504.05335 . Бибкод : 2015PhRvC..92c1304I . дои : 10.1103/PhysRevC.92.031304 . S2CID 56380507 .
^ Бейнер, М.; Флокард, Х.; Ван Гиай, Нгуен; Квентин, П. (1975). «Свойства основного состояния ядра и самосогласованные расчеты со скирмовым взаимодействием». Ядерная физика А . 238 (1): 29–69. Бибкод : 1975НуФА.238...29Б . дои : 10.1016/0375-9474(75)90338-3 .
^ Вотерен, Д.; Бринк, ДМ (1 марта 1972 г.). «Расчеты Хартри-Фока с учетом взаимодействия Скирма. I. Сферические ядра» . Физический обзор C . 5 (3): 626–647. дои : 10.1103/PhysRevC.5.626 . ISSN 0556-2813 .
^ Дечарже, Дж.; Гоньи, Д. (1 апреля 1980 г.). "Расчеты Хартри-Фока-Боголюбова с эффективным взаимодействием $D1$ на сферических ядрах" . Физический обзор C . 21 (4): 1568–1593. дои : 10.1103/PhysRevC.21.1568 .
^ Бролья, Рикардо А.; Зелевинский, Владимир (2013). Пятьдесят лет ядерной БКШ: спаривание в конечных системах . Всемирная научная. дои : 10.1142/8526 . ISBN 978-981-4412-48-3 .
^ «Метод Хартри-Фока-Боголюбова» .
^ Бэйман, Б.Ф. (1960). «Вывод метода парной корреляции». Нукл. Физ . 15 : 33–38. Бибкод : 1960NucPh..15...33B . дои : 10.1016/0029-5582(60)90279-0 .

Внешние ссылки [ править ]

Английский

(на английском языке) Институт ядерной физики (IPN), Франция
(на английском языке) Центр исследований антипротонов и ионов (FAIR), Германия
(на английском языке) Общество исследований тяжелых ионов (GSI), Германия
(на английском языке) Объединенный институт ядерных исследований (ОИЯИ), Россия
(на английском языке) Аргоннская национальная лаборатория (ANL), США
(на английском языке) Королевство, Япония
(на английском языке) Национальная лаборатория сверхпроводящих циклотронов, Университет штата Мичиган, США
(на английском языке) Установка для пучков редких изотопов, Университет штата Мичиган, США

Французский

(на французском языке) Институт ядерной физики (IPN), Франция
(на французском языке) Центр ядерной спектрометрии и масс-спектрометрии (CSNSM), Франция
(на французском языке) Департамент ядерной физики CEA/DAM, Франция
(на французском языке) Национальный институт ядерной физики и физики элементарных частиц (In2p3), Франция
(на французском языке) Большой национальный ускоритель тяжелых ионов (GANIL), Франция
(на французском языке) Комиссия по атомной энергии (CEA), Франция
(на французском языке) Европейский центр ядерных исследований, Швейцария
ЖИВАЯ карта нуклидов - МАГАТЭ

[1] Эренштейн, Дэвид (21 ноября 2023 г.). «Основное состояние ядра имеет структуру, подобную молекуле» . Проверено 23 ноября 2023 г.

[2] Ли, Пэнцзе (2023). «Подтверждение молекулярной структуры основного состояния 10Be с использованием измерений сечения тройной дифференциальной реакции 10Be(p,pα)6He». Письма о физических отзывах . arXiv : 2311.13129 . doi : 10.1103/PhysRevLett.131.212501 .

[3] Эбран, JP (2012). «Как кластеризуются атомные ядра». Природа . 487 : 341–344. arXiv : 1203.1244 . дои : 10.1038/nature11246 .

[4] Вильдермут, К. (1958). «Кластерная модель» атомных ядер». Ядерная физика . 7 : 150–162. дои : 10.1016/0029-5582(58)90245-1 .

[5] фон Вайцзеккер, CF (1935). «К теории ядерных масс». Журнал физики (на немецком языке). 96 (7–8): 431–458. Бибкод : 1935ZPhy...96..431W . дои : 10.1007/BF01337700 . S2CID 118231854 .

[6] Мёллер, П.; Майерс, WD; Святецкий, WJ; Трейнер, Дж. (3 сентября 1984 г.). «Модель капли конечного радиуса действия». Конференция: 7. Международная конференция по атомным массам и фундаментальным константам (AMCO-7), Дармштадт-Зеехайм, Франция. Германия . ОСТИ 6441187 .

[7] Гейзенберг, В. (1 января 1932 г.). «О строении атомных ядер. I» . Журнал физики (на немецком языке). 77 (1): 1–11. дои : 10.1007/BF01342433 . ISSN 0044-3328 .

[8] Сорлин, О.; Порке, М.-Ж. (2008). «Ядерная магия чисел: новые возможности, далекие от стабильности». Прогресс в области физики элементарных частиц и ядерной физики . 61 (2): 602–673. arXiv : 0805.2561 . Бибкод : 2008ПрПНП..61..602С . дои : 10.1016/j.ppnp.2008.05.001 . S2CID 118524326 .

[9] Бринк, Дэвид; Бролья, Рикардо А. (2005). Ядерная сверхтекучесть . Издательство Кембриджского университета. ISBN 9781139443074 .

[10] Кольцо, П.; Шук, П. (1980). Ядерная проблема многих тел . Спрингер Верлаг. ISBN 978-3-540-21206-5 .

[NFT-11] Перейти обратно: Перейти обратно: ^а ^б Идини, А.; Потель, Г.; Барранко, Ф.; Вигецци, Э.; Бролья, РА (2015). «Переплетение элементарных мод возбуждения в сверхтекучих ядрах посредством взаимодействия частиц и колебаний: количественный учет разнообразия наблюдаемых структур ядра». Физический обзор C . 92 (3): 031304. arXiv : 1504.05335 . Бибкод : 2015PhRvC..92c1304I . дои : 10.1103/PhysRevC.92.031304 . S2CID 56380507 .

[12] Бейнер, М.; Флокард, Х.; Ван Гиай, Нгуен; Квентин, П. (1975). «Свойства основного состояния ядра и самосогласованные расчеты со скирмовым взаимодействием». Ядерная физика А . 238 (1): 29–69. Бибкод : 1975НуФА.238...29Б . дои : 10.1016/0375-9474(75)90338-3 .

[13] Вотерен, Д.; Бринк, ДМ (1 марта 1972 г.). «Расчеты Хартри-Фока с учетом взаимодействия Скирма. I. Сферические ядра» . Физический обзор C . 5 (3): 626–647. дои : 10.1103/PhysRevC.5.626 . ISSN 0556-2813 .

[14] Дечарже, Дж.; Гоньи, Д. (1 апреля 1980 г.). "Расчеты Хартри-Фока-Боголюбова с эффективным взаимодействием $D1$ на сферических ядрах" . Физический обзор C . 21 (4): 1568–1593. дои : 10.1103/PhysRevC.21.1568 .

[15] Бролья, Рикардо А.; Зелевинский, Владимир (2013). Пятьдесят лет ядерной БКШ: спаривание в конечных системах . Всемирная научная. дои : 10.1142/8526 . ISBN 978-981-4412-48-3 .

[16] «Метод Хартри-Фока-Боголюбова» .

[17] Бэйман, Б.Ф. (1960). «Вывод метода парной корреляции». Нукл. Физ . 15 : 33–38. Бибкод : 1960NucPh..15...33B . дои : 10.1016/0029-5582(60)90279-0 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]