Смачивание

«Влажность» перенаправляется сюда. Чтобы узнать о биологической секреции, см. субпрепуциальную влажность .

Чтобы узнать о других значениях, см. Смачивание (значения) .

Чтобы узнать о других значениях слова «Мокрый», см. Мокрый (значения) .

Капли воды на ткани, не смачиваемой химической обработкой.

Смачивание — это способность жидкости вытеснять газ для поддержания контакта с твердой поверхностью , возникающая в результате межмолекулярных взаимодействий, когда они соединяются. Это происходит при наличии газообразной фазы или другой жидкой фазы, не смешивающейся с первой. Степень смачивания (смачиваемость) определяется балансом сил между адгезионными и когезионными силами . Существует два типа смачивания: нереактивное смачивание и реактивное смачивание.

Смачивание важно для склеивания или склеивания двух материалов. Смачивание и поверхностные силы, которые контролируют смачивание, также ответственны за другие связанные эффекты, включая капиллярные эффекты. Поверхностно-активные вещества можно использовать для увеличения смачивающей способности жидкости, такой как вода.

Смачивание находится в центре внимания исследователей в области нанотехнологий и нанонауки в связи с появлением за последние два десятилетия многих наноматериалов (например, графена , углеродные нанотрубки из нитрида бора , наносетка ).

Объяснение

Рисунок 1. Угол контакта капли жидкости на твердой поверхности.

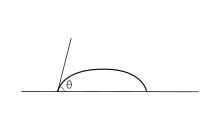
Силы сцепления между жидкостью и твердым телом заставляют каплю жидкости растекаться по поверхности. Силы сцепления внутри жидкости заставляют каплю скатываться и избегать контакта с поверхностью.

Рис. 2	Угол контакта	Степень смачивание	Сила взаимодействия
			Твердое тело-жидкость	жидкость-жидкость
С	θ = 0	Идеальное смачивание	Сильный	Слабый
С	0 < θ < 90°	Высокая смачиваемость	Сильный	Сильный
			Слабый	Слабый
Б	90° ≤ θ < 180°	Низкая смачиваемость	Слабый	Сильный
А	θ = 180°	Не смачивающий	Слабый	Сильный

Рисунок 2: Смачивание различных жидкостей: A показывает жидкость с очень небольшим смачиванием, а C показывает жидкость с большим смачиванием. A имеет большой угол контакта, а C имеет небольшой угол контакта.

Угол контакта (θ), как показано на рисунке 1, представляет собой угол, под которым граница раздела жидкость-пар встречается с границей раздела твердое тело-жидкость. Угол контакта определяется балансом между адгезионными и когезионными силами. По мере увеличения склонности капли к растеканию по плоской твердой поверхности угол контакта уменьшается. Таким образом, контактный угол обеспечивает обратную меру смачиваемости.

Угол контакта менее 90° (малый угол контакта) обычно указывает на то, что смачивание поверхности очень благоприятно, и жидкость распространится по большой площади поверхности. Углы контакта более 90° (высокий угол контакта) обычно означают, что смачивание поверхности неблагоприятно, поэтому жидкость сводит к минимуму контакт с поверхностью и образует компактную каплю жидкости.

Что касается воды, смачиваемую поверхность можно также назвать гидрофильной , а несмачиваемую поверхность - гидрофобной . Супергидрофобные поверхности имеют углы смачивания более 150°, что означает практически полное отсутствие контакта между каплей жидкости и поверхностью. Иногда это называют « эффектом лотоса ». В таблице описаны различные углы контакта и соответствующие им взаимодействия твердое тело/жидкость и жидкость/жидкость. Для неводных жидкостей термин «лиофильные» используется для условий с малым углом смачивания, а термин «лиофобный» используется, когда возникают более высокие углы смачивания. Точно так же термины омнифобный и омнифильный применяются как к полярным , так и к неполярным жидкостям.

Высокоэнергетические и низкоэнергетические поверхности

Жидкости могут взаимодействовать с двумя основными типами твердых поверхностей. Традиционно твердые поверхности делят на твердые тела с высокой и низкой энергией. Относительная энергия твердого тела связана с объемной природой самого твердого тела. Твердые тела, такие как металлы, стекла и керамика, известны как «твердые тела», потому что химические связи , которые удерживают их вместе (например, ковалентные , ионные или металлические ), очень прочны. Таким образом, для разрушения этих твердых тел требуется большое количество энергии (альтернативно, требуется большое количество энергии, чтобы разрезать объем и создать две отдельные поверхности), поэтому их называют «высокоэнергетическими». Большинство молекулярных жидкостей достигают полного смачивания высокоэнергетических поверхностей.

Другой тип твердых веществ — это слабые молекулярные кристаллы (например, фторуглероды , углеводороды и т. д.), в которых молекулы удерживаются вместе главным образом физическими силами (например, силами Ван-дер-Ваальса и водородными связями ). Поскольку эти твердые тела удерживаются вместе слабыми силами, для их разрушения требуется очень небольшое количество энергии, поэтому их называют «низкоэнергетическими». В зависимости от типа выбранной жидкости низкоэнергетические поверхности могут допускать как полное, так и частичное смачивание.

Сообщалось о динамических поверхностях, поверхностная энергия которых претерпевает изменения при приложении соответствующих стимулов. Например, было показано, что поверхность, имеющая молекулярные двигатели, управляемые фотонами , претерпевает изменения угла контакта с водой при переключении между бистабильными конформациями с различными поверхностными энергиями.

Смачивание низкоэнергетических поверхностей

Низкоэнергетические поверхности взаимодействуют с жидкостями преимущественно посредством дисперсионных ( ван-дер-ваальсовых ) сил. Уильям Зисман сделал несколько ключевых выводов:

Зисман заметил, что cos θ линейно увеличивается по мере уменьшения поверхностного натяжения (γ _LV ) жидкости. Таким образом, ему удалось установить линейную зависимость между cos θ и поверхностным натяжением (γ _LV ) для различных органических жидкостей.

Поверхность более смачивается, когда γ _LV и θ низкие. Зисман назвал точку пересечения этих линий, когда cos θ = 1, критическим поверхностным натяжением (γc ₎ этой поверхности. Это критическое поверхностное натяжение является важным параметром, поскольку оно характерно только для твердого тела.

Зная критическое поверхностное натяжение твердого тела, можно прогнозировать смачиваемость поверхности. Смачиваемость поверхности определяется крайними химическими группами твердого тела. Различия в смачиваемости поверхностей, сходных по структуре, обусловлены различиями в упаковке атомов. Например, если поверхность имеет разветвленные цепи, она будет иметь худшую упаковку, чем поверхность с прямыми цепями. Более низкое критическое поверхностное натяжение означает меньшую смачиваемость поверхности материала.

Идеальные твердые поверхности

Идеальная поверхность плоская, жесткая, идеально гладкая, химически однородная и имеет нулевой гистерезис угла смачивания . Нулевой гистерезис означает, что углы контакта при наступлении и отступлении равны. Другими словами, существует только один термодинамически стабильный контактный угол. Когда капля жидкости помещается на такую ​​поверхность, характерный угол контакта формируется, как показано на рисунке 1. Кроме того, на идеальной поверхности капля вернется к своей первоначальной форме, если ее нарушить. Следующие выводы применимы только к идеальным твердым поверхностям; они справедливы только для состояния, в котором границы раздела неподвижны и линия границы раздела фаз существует в равновесии.

Минимизация энергии, три этапа

Рисунок 3: Сосуществование трех жидких фаз во взаимном контакте; здесь α, β и θ указывают как фазу, так и угол контакта.

Рисунок 4: Треугольник Неймана, связывающий поверхностные энергии и углы смачивания трех жидких фаз, сосуществующих в статическом равновесии, как показано на рисунке 3.

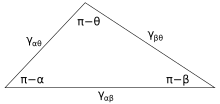
На рисунке 3 показана линия контакта трех фаз. В состоянии равновесия чистая сила на единицу длины, действующая вдоль линии границы между тремя фазами, должна быть равна нулю. Компоненты чистой силы в направлении вдоль каждого из интерфейсов определяются как:

${\begin{aligned}\gamma _{\alpha \theta }+\gamma _{\theta \beta }\cos \left(\theta \right)+\gamma _{\alpha \beta }\cos \left(\alpha \right)&=0\\\gamma _{\alpha \theta }\cos \left(\theta \right)+\gamma _{\theta \beta }+\gamma _{\alpha \beta }\cos \left(\beta \right)&=0\\\gamma _{\alpha \theta }\cos \left(\alpha \right)+\gamma _{\theta \beta }\cos \left(\beta \right)+\gamma _{\alpha \beta }&=0\end{aligned}}$

где α, β и θ — показанные углы, а γ _ij — поверхностная энергия между двумя указанными фазами. Эти отношения также могут быть выражены аналогом треугольника, известного как треугольник Неймана, показанного на рисунке 4. Треугольник Неймана согласуется с геометрическим ограничением, согласно которому $\alpha +\beta +\theta =2\pi$и применение к нему закона синусов и закона косинусов дает соотношения, описывающие, как межфазные углы зависят от соотношения поверхностных энергий.

Поскольку эти три поверхностные энергии образуют стороны треугольника , они ограничены неравенствами треугольника: γ _ij < γ _jk + γ _ik, что означает, что ни одно из поверхностных натяжений не может превышать сумму двух других. Если три жидкости с поверхностной энергией, которая не соответствует этим неравенствам, будут приведены в контакт, не будет существовать равновесной конфигурации, соответствующей рисунку 3.

Упрощение до плоской геометрии, соотношение Юнга

Рисунок 5. Угол контакта капли жидкости, смоченной твердой твердой поверхностью.

Если β-фазу заменить плоской жесткой поверхностью, как показано на рисунке 5, тогда β = π, и второе уравнение суммарной силы упрощается до уравнения Юнга:

$\gamma _{SG}=\gamma _{SL}+\gamma _{LG}\cos \left(\theta \right)$

который связывает поверхностное натяжение между тремя фазами: твердой , жидкой и газообразной . Впоследствии это позволяет предсказать угол контакта капли жидкости с твердой поверхностью на основе знания трех задействованных поверхностных энергий. Это уравнение также применимо, если «газовая» фаза представляет собой другую жидкость, несмешивающуюся с каплей первой «жидкой» фазы.

Упрощение плоской геометрии, соотношение Юнга, полученное на основе вариационных вычислений.

Рассматривайте интерфейс как кривую $y(x)$ для $x\in I=[0,L]$ где $L$ является свободным параметром. Свободная энергия, которую необходимо минимизировать, равна

${\cal {F}}[y,L]=\int _{0}^{L}\left(\gamma _{LG}{\sqrt {1+y'^{2}}}+(\gamma _{SL}-\gamma _{SG})\right)dx$

с ограничениями $y(0)=y(L)=0$ который мы можем записать как $\int _{I}y'dx=0$ и фиксированный объем $\int _{I}ydx=A$.

Таким образом, модифицированный лагранжиан с учетом ограничений имеет вид

${\cal {L}}=\gamma _{LG}{\sqrt {1+y'^{2}}}+(\gamma _{SL}-\gamma _{SG})-\lambda _{1}y'-\lambda _{2}y$

где $\lambda _{i}$ являются множителями Лагранжа. По определению, импульс $p=\partial _{y'}{\cal {L}}$ и гамильтониан ${\cal {H}}=py'-{\cal {L}}$ который рассчитывается как:

${\cal {H}}=-\gamma _{LG}{\frac {1}{\sqrt {1+y'^{2}}}}-(\gamma _{SL}-\gamma _{SG})+\lambda _{2}y$

Теперь напомним, что граница свободна в $x$ направление и $L$ является свободным параметром. Следовательно, мы должны иметь:

${\frac {\partial {\cal {F}}}{\partial L}}=-{\cal {H}}=0$

На границе $y(L)=0$ и $(1+y'^{2})^{-1/2}=\cos \theta$, поэтому восстанавливаем уравнение Юнга.

Неидеально гладкие поверхности и контактный угол Юнга

Уравнение Юнга предполагает идеально плоскую и жесткую поверхность, часто называемую идеальной поверхностью . Во многих случаях поверхности далеки от этой идеальной ситуации, и здесь рассматриваются два случая: случай шероховатых поверхностей и случай гладких поверхностей, которые еще являются реальными (конечно жесткими). Даже на идеально гладкой поверхности капля будет принимать широкий спектр углов смачивания: от так называемого опережающего угла смачивания до $\theta _{\mathrm {A} }$, к так называемому углу смачивания, $\theta _{\mathrm {R} }$. Равновесный контактный угол ( $\theta _{\mathrm {c} }$) можно вычислить по формуле $\theta _{\mathrm {A} }$ и $\theta _{\mathrm {R} }$ как показал Тадмор как,

$\theta _{\mathrm {c} }=\arccos \left({\frac {r_{\mathrm {A} }\cos \left(\theta _{\mathrm {A} }\right)+r_{\mathrm {R} }\cos \left(\theta _{\mathrm {R} }\right)}{r_{\mathrm {A} }+r_{\mathrm {R} }}}\right)$

где

$r_{\mathrm {A} }=\left({\frac {\sin ^{3}\left(\theta _{\mathrm {A} }\right)}{2-3\cos \left(\theta _{\mathrm {A} }\right)+\cos ^{3}\left(\theta _{\mathrm {A} }\right)}}\right)^{\frac {1}{3}}~;~~r_{\mathrm {R} }=\left({\frac {\sin ^{3}\left(\theta _{\mathrm {R} }\right)}{2-3\cos \left(\theta _{\mathrm {R} }\right)+\cos ^{3}\left(\theta _{\mathrm {R} }\right)}}\right)^{\frac {1}{3}}$

Уравнение Юнга – Дюпре и коэффициент расширения.

Уравнение Янга-Дюпре ( Томас Янг , 1805; Антанас Дюпре и Поль Дюпре, 1869) показывает, что ни γ _SG, ни γ _SL не могут быть больше суммы двух других поверхностных энергий. Следствием этого ограничения является предсказание полного смачивания, когда γ _SG > γ _SL + γ _LG , и нулевого смачивания, когда γ _SL > γ _SG + γ _LG . Отсутствие решения уравнения Янга – Дюпре является показателем того, что для этих ситуаций не существует равновесной конфигурации с углом контакта от 0 до 180 °.

Полезным параметром для измерения смачивания является параметр растекания S ,

$S=\gamma _{SG}-\left(\gamma _{SL}+\gamma _{LG}\right)$

При S > 0 жидкость полностью смачивает поверхность (полное смачивание). При S < 0 происходит частичное смачивание.

Объединение определения параметра расширения с соотношением Юнга дает уравнение Янга – Дюпре:

$S=\gamma _{LG}\left(\cos \left(\theta \right)-1\right)$

который имеет физические решения для θ только тогда, когда S <0.

Обобщенная модель угла контакта капель на плоских и искривленных поверхностях.

Благодаря усовершенствованиям в методах измерения, таких как АСМ, конфокальная микроскопия и СЭМ, исследователи смогли создавать и отображать капли в еще меньших масштабах. С уменьшением размера капель появились новые экспериментальные наблюдения за смачиванием. Эти наблюдения подтверждают, что модифицированное уравнение Юнга не выдерживает микро-наномасштабов. Кроме того, модифицированное уравнение Юнга не поддерживает знак натяжения линии.

Для сидячей капли свободная энергия трехфазной системы может быть выражена как:

$\delta w=\gamma _{LV}dA_{LV}+\gamma _{SL}dA_{SL}+\gamma _{SV}dA_{SV}-\kappa dL-PdV-VdP$

При постоянном объеме в термодинамическом равновесии это сводится к:

$0={\frac {dA_{LG}}{dA_{SL}}}+{\frac {\gamma _{SL}-\gamma _{SG}}{\gamma _{LG}}}-{\frac {\kappa }{\gamma _{LG}}}{\frac {dL}{dA_{SL}}}-{\frac {V}{\gamma _{LG}}}{\frac {dP}{dA_{SL}}}$

Обычно термином VdP пренебрегают для больших капель, однако работа VdP становится значимой в небольших масштабах. Изменение давления при постоянном объеме на свободной границе жидкость-пар обусловлено давлением Лапласа , которое пропорционально средней кривизне капли и не равно нулю. Решение приведенного выше уравнения как для выпуклых, так и для вогнутых поверхностей дает:

$\cos(\theta \mp \alpha )=A+B{\frac {\cos(\alpha )}{a}}\pm C\sin(\theta \mp \alpha )(\cos(\theta )+1)^{2}{\biggl (}{\frac {\sin(\alpha )(\cos(\alpha )+2)}{(\cos(\alpha )+1)^{2}}}\mp {\frac {\sin(\theta )(\cos(\theta )+2)}{(\cos(\theta )+1)^{2}}}{\biggr )}$

Где постоянные параметры A, B и C определяются как:

Принципиальные изображения капель на плоских (а), вогнутых (б) и выпуклых (в) поверхностях

$A={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}$, $B={\frac {\kappa }{\gamma _{LG}}}$ и $C={\frac {\gamma }{3\gamma _{LG}}}$

Это уравнение связывает угол контакта $\theta$, геометрическое свойство сидячей капли по отношению к объемной термодинамике, энергия на границе трехфазного контакта и кривизна поверхности α. Для частного случая сидячей капли на плоской поверхности (α=0)

$\cos(\theta )={\frac {\gamma _{SG}-\gamma _{SL}}{\gamma _{LG}}}+{\frac {\kappa }{\gamma _{LG}}}{\frac {1}{a}}-{\frac {\gamma }{3\gamma _{LG}}}(2+\cos(\theta )-2\cos ^{2}(\theta )-\cos ^{3}(\theta ))$

Первые два члена представляют собой модифицированное уравнение Юнга: а третий член обусловлен давлением Лапласа. Это нелинейное уравнение правильно предсказывает знак и величину κ, выравнивание угла контакта в очень малых масштабах и гистерезис угла контакта.

Вычислительный прогноз смачивания

Для многих конфигураций поверхность/адсорбат данные о поверхностной энергии и экспериментальные наблюдения недоступны. Поскольку смачивающие взаимодействия имеют большое значение в различных приложениях, часто желательно предсказать и сравнить поведение смачивания различных поверхностей материалов с определенной кристаллографической ориентацией по отношению к воде или другим адсорбатам. Это можно сделать с атомистической точки зрения с помощью таких инструментов, как молекулярная динамика и теория функционала плотности . В теоретическом прогнозировании смачивания с помощью ab initio подходов, таких как DFT, воду обычно заменяют льдом. Это связано с тем, что расчеты DFT обычно проводятся в предположении условий нулевого теплового движения атомов, что, по сути, означает, что моделирование проводится при абсолютном нуле . Тем не менее, это упрощение дает результаты, которые актуальны для адсорбции воды в реальных условиях, а использование льда для теоретического моделирования смачивания является обычным явлением.

Неидеальные шероховатые твердые поверхности

Рисунок 6: Схема наступающих и отступающих углов контакта.

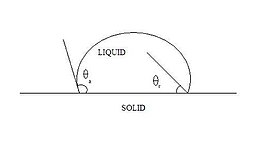
В отличие от идеальных поверхностей, реальные поверхности не обладают идеальной гладкостью, жесткостью и химической однородностью. Такие отклонения от идеальности приводят к явлению, называемому гистерезисом угла контакта , который определяется как разница между наступающим (θ _a ) и отступающим (θ _r ) углами контакта.

${\text{H}}=\,\theta _{a}-\,\theta _{r}$

Когда угол контакта находится между случаями наступления и отступления, линия контакта считается закрепленной, и можно наблюдать гистерезисное поведение, а именно гистерезис угла контакта . При превышении этих значений смещение линии контакта, например, как на рисунке 3, будет происходить либо за счет расширения, либо за счет втягивания капли. На рис. 6 показаны наступающие и отступающие углы контакта. Наступающий угол контакта является максимальным стабильным углом, тогда как угол отступления является минимальным стабильным углом. Гистерезис краевого угла возникает потому, что в неидеальном твердом теле обнаруживается множество различных термодинамически стабильных углов смачивания. Эти изменяющиеся термодинамически стабильные углы смачивания известны как метастабильные состояния.

Такое движение границы фаз, включающее надвигающиеся и удаляющиеся углы смачивания, известно как динамическое смачивание. Разница между динамическим и статическим углами смачивания пропорциональна капиллярному числу . $Ca$, Когда линия контакта продвигается вперед, покрывая большую часть поверхности жидкостью, угол контакта увеличивается и обычно связан со скоростью линии контакта. Если скорость линии контакта неограниченно увеличивается, угол контакта увеличивается, и по мере приближения к 180 ° газовая фаза увлекается тонким слоем между жидкостью и твердым телом. Это кинетический неравновесный эффект, возникающий в результате движения линии контакта с такой высокой скоростью, что полное смачивание произойти не может.

Хорошо известным отклонением от идеальных условий является то, что интересующая поверхность имеет шероховатую текстуру. Шероховатая текстура поверхности может относиться к одной из двух категорий: гомогенной или неоднородной. Однородный режим смачивания – это когда жидкость заполняет канавки шероховатой поверхности. Однако при гетерогенном режиме смачивания поверхность представляет собой смесь двух типов пятен. Важным примером такой составной поверхности является поверхность, состоящая из участков воздуха и твердого тела. Такие поверхности по-разному влияют на углы контакта смачивающих жидкостей. Кэсси-Бакстер и Венцель — две основные модели, которые пытаются описать смачивание текстурированных поверхностей. Однако эти уравнения применимы только в том случае, если размер капли достаточно велик по сравнению с масштабом шероховатости поверхности. Когда размер капель сравним с размером капель нижележащих столбов, следует учитывать влияние натяжения лески.

Модель Венцеля

Рисунок 7: Модель Венцеля

Модель Венцеля (Роберт Н. Венцель, 1936 г.) описывает режим однородного смачивания, как показано на рисунке 7, и определяется следующим уравнением для угла контакта на шероховатой поверхности:

$\cos \,\left(\theta ^{*}\right)=r\cos \,\left(\theta \right)$

где $\theta ^{*}$ - кажущийся угол контакта, который соответствует состоянию устойчивого равновесия (т.е. состоянию минимальной свободной энергии системы). Коэффициент шероховатости r является мерой того, как шероховатость поверхности влияет на однородную поверхность. Коэффициент шероховатости определяется как отношение истинной площади твердой поверхности к видимой площади.

θ — контактный угол Юнга , определенный для идеальной поверхности. Хотя уравнение Венцеля показывает, что угол контакта шероховатой поверхности отличается от внутреннего угла контакта, оно не описывает гистерезис угла контакта .

Модель Кэсси – Бакстера

Рисунок 8: Модель Кэсси-Бакстера.

При работе с неоднородной поверхностью модели Венцеля недостаточно. Необходима более сложная модель для измерения того, как изменяется видимый угол контакта при использовании различных материалов. Эта неоднородная поверхность, подобная той, что показана на рисунке 8, объясняется с помощью уравнения Кэсси-Бакстера ( закона Кэсси ):

$\cos \,\left(\theta ^{*}\right)=r_{f}\,f\,\cos \,\left(\theta _{\text{Y}}\right)+f-1$

Здесь r _f — коэффициент шероховатости площади влажной поверхности, а f — доля площади твердой поверхности, смоченной жидкостью. Когда f = 1 и r _f = r , уравнения Кэсси-Бакстера становятся уравнением Венцеля. С другой стороны, когда имеется много различных фракций шероховатости поверхности, каждая доля общей площади поверхности обозначается как $f_{i}$.

Суммирование всех $f_{i}$ равен 1 или общей поверхности. Кэсси-Бакстер также можно преобразовать в следующее уравнение:

$\gamma \cos \,\left(\theta ^{*}\right)=\sum _{n=1}^{N}f_{i}\left(\gamma _{\text{i,sv}}-\gamma _{\text{i,sl}}\right)$

Здесь $\gamma$ - поверхностное натяжение Кэсси – Бакстера между жидкостью и паром, $\gamma _{i,sv}$ - поверхностное натяжение твердого пара каждого компонента, и $\gamma _{i,sl}$ — поверхностное натяжение твердого тела и жидкости каждого компонента. Стоит упомянуть случай, когда капля жидкости помещается на подложку и создает под ней небольшие воздушные карманы. Этот случай для двухкомпонентной системы обозначается:

$\gamma \cos \,\left(\theta ^{*}\right)=f_{1}\left(\gamma _{\text{1,sv}}-\gamma _{\text{1,sl}}\right)-\left(1-f_{1}\right)\gamma$

Здесь ключевое отличие, на которое следует обратить внимание, заключается в том, что для второго компонента поверхностного натяжения между твердым телом и паром нет поверхностного натяжения. Это связано с предположением, что открытая поверхность воздуха находится под каплей и является единственным другим субстратом в системе. Впоследствии уравнение выражается как (1 – f ). Следовательно, уравнение Кэсси можно легко вывести из уравнения Кэсси – Бакстера. Экспериментальные результаты, касающиеся свойств поверхности систем Венцеля и Кэсси-Бакстера, показали эффект закрепления для угла Юнга от 180 до 90 °, области, классифицированной в рамках модели Кэсси-Бакстера. Эта композитная система жидкость/воздух в значительной степени гидрофобна. После этого был обнаружен резкий переход к режиму Венцеля, когда капля смачивает поверхность, но не далее краев капли. Фактически уравнения Юнга, Венцеля и Кэсси-Бакстера представляют собой условия трансверсальности вариационной задачи смачивания.

Фильм-предшественник

С появлением изображений с высоким разрешением исследователи начали получать экспериментальные данные, которые заставили их усомниться в предположениях уравнения Кэсси-Бакстера при расчете кажущегося угла контакта. Эти группы полагают, что видимый угол контакта во многом зависит от тройной линии. Тройная линия, соприкасающаяся с неоднородной поверхностью, не может опираться на неоднородную поверхность, как остальная часть капли. По идее, оно должно соответствовать несовершенству поверхности. Этот изгиб тройной линии нежелателен и не наблюдается в реальных ситуациях. Теория, которая сохраняет уравнение Кэсси-Бакстера и в то же время объясняет наличие минимизированного энергетического состояния тройной линии, основана на идее пленки-предшественника. Эта пленка субмикронной толщины опережает движение капли и располагается вокруг тройной линии. Более того, эта пленка-предшественник позволяет тройной линии изгибаться и принимать различные конформации, которые изначально считались неблагоприятными. Эту жидкость-предшественник наблюдали с помощью сканирующей электронной микроскопии окружающей среды (ESEM) на поверхностях с порами, образовавшимися в объеме. С введением концепции пленки-предшественника тройная линия может следовать энергетически возможным конформациям, тем самым правильно объясняя модель Кэсси-Бакстера.

«Эффект лепестка» против «эффекта лотоса»

Рисунок 9: «Эффект лепестка» и «эффект лотоса»

Собственную гидрофобность поверхности можно повысить за счет текстурирования с шероховатостью разной длины . Красная роза использует это преимущество, используя иерархию микро- и наноструктур на каждом лепестке, чтобы обеспечить достаточную шероховатость для супергидрофобности. Точнее, каждый лепесток розы имеет на поверхности набор микрососочков, а каждый сосочек, в свою очередь, имеет множество наноскладок. Термин « эффект лепестка » описывает тот факт, что капля воды на поверхности лепестка розы имеет сферическую форму, но не может скатиться, даже если лепесток перевернуть. Капли воды сохраняют сферическую форму благодаря супергидрофобности лепестка (угол смачивания около 152,4°), но не скатываются, поскольку поверхность лепестка имеет высокую силу сцепления с водой.

Сравнивая « эффект лепестка » с « эффектом лотоса », важно отметить некоторые поразительные различия. Структуру поверхности листа лотоса и лепестка розы, показанную на рисунке 9, можно использовать для объяснения двух разных эффектов.

Лист лотоса имеет случайно шероховатую поверхность и низкий гистерезис угла смачивания , что означает, что капля воды не способна смачивать промежутки микроструктуры между шипами. Это позволяет воздуху оставаться внутри текстуры, создавая неоднородную поверхность, состоящую как из воздуха, так и из твердого тела. В результате сила сцепления между водой и твердой поверхностью чрезвычайно мала, что позволяет воде легко скатываться (т.е. явление « самоочистки »).

Микро- и наноструктуры лепестка розы крупнее, чем у листа лотоса, что позволяет жидкой пленке пропитывать текстуру. Однако, как видно на рисунке 9, жидкость может проникать в канавки большего размера, но не может проникать в канавки меньшего размера. Это известно как режим пропитки Кэсси. Поскольку жидкость может смачивать более крупные канавки, сила сцепления между водой и твердым телом очень высока. Это объясняет, почему капля воды не упадет, даже если лепесток наклонить под углом или перевернуть. Этот эффект не удастся, если объем капли превышает 10 мкл, поскольку баланс между весом и поверхностным натяжением нарушен.

Переход Кэсси-Бакстера к Венцелю

Рисунок 10: Грибовидное состояние

В модели Кэсси-Бакстера капля находится поверх текстурированной поверхности, а под ней находится захваченный воздух. Во время перехода смачивания из состояния Кэсси в состояние Венцеля воздушные карманы перестают быть термодинамически стабильными, и жидкость начинает образовывать зародыши из середины капли, создавая «грибовидное состояние», как показано на рисунке 10. Условие проникновения определяется следующим образом:

$\cos \,\left(\theta _{\text{C}}\right)={\frac {\phi -1}{r-\phi }}$

где

• θ _C — критический угол контакта.
• Φ — доля границы раздела твердое тело/жидкость, при которой капля контактирует с поверхностью.
• r — сплошная шероховатость (для плоской поверхности r = 1)

Рисунок 11: Фронт проникновения распространяется за пределы падения

Фронт проникновения распространяется, минимизируя поверхностную энергию, пока не достигнет краев капли и, таким образом, не достигнет состояния Венцеля. Поскольку твердое вещество можно считать поглощающим материалом из-за шероховатости его поверхности, это явление растекания и впитывания называется гемивикингом. Контактные углы, при которых происходит растекание/пропитка, составляют от 0 до π/2.

Модель Венцеля справедлива между θ _C и π/2. Если контактный угол меньше Θ _C , фронт проникновения выходит за пределы капли и на поверхности образуется пленка жидкости. На рис. 11 изображен переход из состояния Венцеля в состояние поверхностной пленки. Пленка сглаживает шероховатости поверхности и модель Венцеля больше не применяется. В этом состоянии условие равновесия и соотношение Юнга дают:

$\cos \,\left(\theta ^{*}\right)=\phi \cos \,\left(\theta _{C}\right)+\left(1-\phi \right)$

Путем точной настройки шероховатости поверхности можно добиться перехода как между супергидрофобными, так и супергидрофильными областями. Как правило, чем шероховатее поверхность, тем она более гидрофобна.

Динамика распространения

Если каплю положить на гладкую горизонтальную поверхность, она, как правило, не находится в состоянии равновесия. Следовательно, он распространяется до тех пор, пока не будет достигнут равновесный радиус контакта (частичное смачивание). С учетом капиллярного, гравитационного и вязкого вкладов радиус капли как функция времени можно выразить как

$r(t)=r_{e}\left[1-\exp \left(-\left({\frac {2\gamma _{LG}}{r_{e}^{12}}}+{\frac {\rho g}{9r_{e}^{10}}}\right){\frac {24\lambda V^{4}\left(t+t_{0}\right)}{\pi ^{2}\eta }}\right)\right]^{\frac {1}{6}}.$

Для ситуации полного смачивания радиус капли в любой момент процесса растекания определяется выражением

$r(t)=\left[\left(\gamma _{LG}{\frac {96\lambda V^{4}}{\pi ^{2}\eta }}\left(t+t_{0}\right)\right)^{\frac {1}{2}}+\left({\frac {\lambda (t+t_{0})}{\eta }}\right)^{\frac {2}{3}}{\frac {24\rho gV^{\frac {3}{8}}}{7\cdot 96^{\frac {1}{3}}\pi ^{\frac {4}{3}}\gamma _{LG}^{\frac {1}{3}}}}\right]^{\frac {1}{6}},$

где

• γ _LG – поверхностное натяжение жидкости
• V — объем капли
• η — вязкость жидкости
• ρ — плотность жидкости
• g — гравитационная постоянная
• λ — коэффициент формы, 37,1   м ⁻¹
• t ₀ – экспериментальное время задержки
• r _e — радиус капли в равновесии

Изменение смачивающих свойств

ПАВ

Многие технологические процессы требуют контроля растекания жидкости по твердым поверхностям. Когда капля помещается на поверхность, она может полностью смачивать, частично смачивать или не смачивать поверхность. Уменьшая поверхностное натяжение с помощью поверхностно-активных веществ , можно добиться частичного или полного смачивания несмачивающего материала. Избыточная свободная энергия (σ) капли на твердой поверхности равна:

$\sigma =\gamma S+PV+\pi \,R^{2}\left(\gamma _{\text{SL}}-\gamma _{\text{SV}}\right)$

• γ – межфазное натяжение жидкость–пар.
• γ _SL — межфазное натяжение твердое тело и жидкость.
• γ _SV – межфазное натяжение твердое тело–пар.
• S – площадь границы раздела жидкость–пар.
• P — избыточное давление внутри жидкости
• R - радиус основания капли.

Согласно этому уравнению, избыточная свободная энергия минимизируется, когда γ уменьшается, γ _SL уменьшается или γ _SV увеличивается. Поверхностно-активные вещества абсорбируются на границах раздела жидкость-пар, твердое-жидкость и твердое-пар, что изменяет смачивающие свойства гидрофобных материалов, уменьшая свободную энергию. Когда поверхностно-активные вещества абсорбируются гидрофобной поверхностью, полярные головные группы обращены в раствор, а хвост обращен наружу. На более гидрофобных поверхностях поверхностно-активные вещества могут образовывать двойной слой на твердом веществе, в результате чего оно становится более гидрофильным. Динамический радиус падения можно охарактеризовать как начало растекания капли. Таким образом, угол контакта изменяется по следующему уравнению:

$\cos \,\left(\theta (t)\right)=\cos \,\left(\theta _{0}\right)+\left(\cos \,\left(\theta _{\infty }\right)-\cos \,\left(\theta _{0}\right)\right)\left(1-\mathrm {e} ^{-{\frac {t}{\tau }}}\right)$

• θ ₀ — начальный угол контакта
• θ _∞ — конечный угол контакта.
• τ — масштаб времени переноса поверхностно-активного вещества

По мере поглощения ПАВ поверхностное натяжение твердого тела и пара увеличивается и края капли становятся гидрофильными. В результате капля распространяется.

Изменения поверхности

Нити незаряженного ферроцензамещенного полимера прикреплены к гидрофобной поверхности диоксида кремния . Окисление ферроценильных групп приводит к образованию гидрофильной поверхности из-за электростатического притяжения между образовавшимися зарядами и полярным растворителем.

Ферроцен – окислительно -восстановительное металлоорганическое соединение. который можно включать в различные мономеры и использовать для создания полимеров , которые можно прикрепить к поверхности. Винилферроцен (ферроценилэтен) можно получить по реакции Виттига. с образованием поливинилферроцена (ПВФ), аналога полистирола а затем полимеризуется . Другим полимером, который может быть получен, является поли( 2-(метакрилоилокси)этилферроценкарбоксилат ), PFcMA. И PVFc, и PFcMA были прикреплены к пластинам диоксида кремния , а смачиваемость измерялась, когда полимерные цепи не заряжены и когда ферроценовые фрагменты окисляются с образованием положительно заряженных групп, как показано справа. Угол контакта с водой на пластинах, покрытых PFcMA, после окисления был на 70° меньше, тогда как в случае PVFc уменьшение составило 30°, и было показано, что переключение смачиваемости является обратимым. В случае PFcMA было исследовано влияние более длинных цепей с большим количеством ферроценовых групп (а также с большей молярной массой ), и было обнаружено, что более длинные цепи приводят к значительно большему уменьшению угла смачивания.

Кислородные вакансии

Оксиды редкоземельных элементов обладают внутренней гидрофобностью и, следовательно, могут использоваться в термически стабильных теплообменниках и других устройствах, связанных с высокотемпературной гидрофобностью. Присутствие кислородных вакансий на поверхности оксидов церия или других редкоземельных элементов играет важную роль в регулировании смачиваемости поверхности. Адсорбция воды на оксидных поверхностях может происходить как молекулярная адсорбция, при которой молекулы H ₂ O остаются неповрежденными на концевой поверхности, или как диссоциативная адсорбция , при которой OH и H адсорбируются отдельно. на твердых поверхностях. Обычно обнаруживается, что присутствие кислородных вакансий усиливает гидрофобность, одновременно способствуя диссоциативной адсорбции.

См. также

• Адсорбция - явление поверхностной адгезии.
• Тело там
• Противотуманные средства – химические вещества, предотвращающие конденсацию воды в виде мелких капель на поверхности.
• Осушение – отвод жидкости от поверхности, которую она была вынуждена покрыть.
• Электросмачивание
• Флотация — направленная вверх сила, противодействующая весу объекта, погруженного в жидкость. Страницы с краткими описаниями целей перенаправления.
• Техника сидячей капли - Метод определения поверхностной энергии твердого тела.
• Мыльный пузырь – тонкая пленка мыльной воды, окружающая воздух.
• Подъем ядра – Лабораторная техника
• Ток смачивания - минимальный электрический ток через контакт, позволяющий преодолеть сопротивление поверхностной пленки.
• Напряжение смачивания – минимальный электрический ток через контакт, необходимый для преодоления сопротивления поверхностной пленки. Страницы с краткими описаниями целей перенаправления.
• Лакский индекс смачиваемости
• Индекс смачиваемости USBM

Дальнейшее чтение

• де Женн, Пьер-Жиль; Брошар-Вайарт, Франсуаза; Кере, Дэвид (2004). Капиллярность и явления смачивания . Спрингер Нью-Йорк. дои : 10.1007/978-0-387-21656-0 . ISBN  978-1-4419-1833-8 . S2CID   137894832 .
• Виктор Михайлович Старов; Мануэль Дж. Веларде ; Клейтон Дж. Радке (2 апреля 2007 г.). Динамика смачивания и растекания . ЦРК Пресс. ISBN  978-1-4200-1617-8 .

Внешние ссылки

• Что такое смачиваемость?
• СМИ, связанные с намоканием, на Викискладе?