Квантовые тепловые двигатели и холодильники

Квантовый тепловой двигатель — это устройство, которое генерирует энергию из теплового потока между горячим и холодным резервуарами. Механизм работы двигателя можно описать законами квантовой механики . На первую реализацию квантового теплового двигателя указали Сковил и Шульц-Дюбуа в 1959 году. показывающая связь эффективности двигателя Карно и 3-уровневого мазера . Квантовые холодильники имеют структуру квантовых тепловых двигателей с целью перекачки тепла из холодной в горячую ванну, потребляя энергию. впервые предложено Гейзиком, Шульцем-Дюбуа, Де Грассом и Сковилем. Когда мощность подается лазером, этот процесс называется оптической накачкой или лазерным охлаждением , предложенным Вайнландом и Хэншем . Удивительно, но тепловые двигатели и холодильники могут работать в масштабе одной частицы, что оправдывает необходимость квантовой теории, называемой квантовой термодинамикой .

Трехуровневый усилитель как квантовый тепловой двигатель

Трехуровневый усилитель. Уровни 1 и 3 соединены с горячим резервуаром. Уровни 1 и 2 соединены с холодным резервуаром. Мощность получается при инверсии населенности между уровнями 3 и 2.

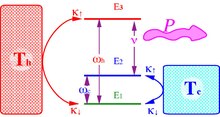
Трехуровневый усилитель — это образец квантового устройства. Он работает за счет использования горячей и холодной ванны. для поддержания инверсии населенностей между двумя энергетическими уровнями, которая используется для усиления света за счет вынужденного излучения. Уровень основного состояния ( 1-g ) и возбужденный уровень ( 3-h ) соединены с горячей ванной с температурой $T_{\text{h}}$. Энергетический разрыв – это $\hbar \omega _{\text{h}}=E_{3}-E_{1}$. Когда население на уровнях уравновешивается

${\frac {N_{\text{h}}}{N_{\text{g}}}}=e^{-{\frac {\hbar \omega _{\text{h}}}{k_{\text{B}}T_{\text{h}}}}}$

где $\hbar ={\frac {h}{2\pi }}$ Планка постоянная и $k_{\text{B}}$ — постоянная Больцмана . Холодная ванна температуры $T_{\text{c}}$ соединяет землю ( 1-g ) с промежуточным уровнем ( 2-c ) с энергетической щелью $E_{2}-E_{1}=\hbar \omega _{\text{c}}$. Когда уровни 2-c и 1-g уравновесятся, тогда

${\frac {N_{\text{c}}}{N_{\text{g}}}}=e^{-{\frac {\hbar \omega _{\text{c}}}{k_{\text{B}}T_{\text{c}}}}}$.

Устройство работает как усилитель , когда уровни ( 3-h ) и ( 2-c ) связаны с внешним полем частоты $\nu$. Для оптимальных условий резонанса $\nu =\omega _{\text{h}}-\omega _{\text{c}}$. Эффективность усилителя в преобразовании тепла в мощность равна отношению выходной работы к потраченному теплу:

$\eta ={\frac {\hbar \nu }{\hbar \omega _{\text{h}}}}=1-{\frac {\omega _{\text{c}}}{\omega _{\text{h}}}}$.

Усиление поля возможно только при положительном коэффициенте усиления (инверсия населенностей). $G=N_{\text{h}}-N_{\text{c}}\geq 0$. Это эквивалентно ${\frac {\hbar \omega _{\text{c}}}{k_{\text{B}}T_{\text{c}}}}\geq {\frac {\hbar \omega _{\text{h}}}{k_{\text{B}}T_{\text{h}}}}$. Подстановка этого выражения в формулу эффективности приводит к:

$\eta =1-{\frac {\omega _{\text{c}}}{\omega _{\text{h}}}}\leq 1-{\frac {T_{\text{c}}}{T_{\text{h}}}}=\eta _{\text{c}}$

где $\eta _{\text{c}}$– цикла Карно эффективность . Равенство получено при условии нулевого усиления $G=0$. Связь между квантовым усилителем и эффективностью Карно была впервые указана Сковилом и Шульцем-Дюбуа:

Реверс операции перемещения тепла из холодной ванны в горячую за счет потребления энергии представляет собой холодильник . Эффективность холодильника, определяемая как коэффициент полезного действия (КПД) для перевернутого устройства, составляет:

$\epsilon ={\frac {\omega _{\text{c}}}{\nu }}\leq {\frac {T_{\text{c}}}{T_{\text{h}}-T_{\text{c}}}}$

Типы

Квантовые устройства могут работать как непрерывно, так и по возвратно-поступательному циклу. К устройствам непрерывного действия относятся солнечные элементы, преобразующие солнечное излучение в электрическую энергию, термоэлектрические , где на выходе используется ток, и лазеры , где выходная мощность представляет собой когерентный свет. Основным примером холодильника непрерывного действия является оптическая накачка и лазерное охлаждение . Подобно классическим поршневым двигателям, квантовые тепловые двигатели также имеют цикл, разделенный на разные такты. Штрих — это отрезок времени, в котором происходит определенная операция (например, термализация или извлечение работы). Два соседних штриха не коммутируют друг с другом. Наиболее распространенными тепловыми машинами с возвратно-поступательным движением являются четырехтактные и двухтактные машины. Было предложено использовать возвратно-поступательные устройства, работающие либо по циклу Карно, либо по циклу Карно. или цикл Отто .

В обоих типах квантовое описание позволяет получить уравнение движения рабочего тела. и тепловой поток от резервуаров.

Квантовый возвратно-поступательный тепловой двигатель и холодильник

См. Также: Поршневой тепловой двигатель.

Квантовые версии большинства распространенных термодинамических циклов были изучены, например, цикл Карно , Цикл Стирлинга и цикл Отто .

Цикл Отто может служить образцом для других циклов возвратно-поступательного движения.

Квантовый цикл Отто, показанный в энтропии $\Omega$ энтропия энергии и энтропия фон Неймана . плоскость, на которой отображаются $\Omega$ является внутренней частотой устройства и управляется извне. Он имитирует обратный объем в цикле Отто . Красная и синяя линии — это горячие и холодные изохоры. Цикл представляет собой тепловой насос.

Он состоит из следующих четырех сегментов:

• Сегмент $A\rightarrow B$ изомагнитный или изохорный процесс , частичное равновесие с холодной ванной при постоянном гамильтониане. Динамику рабочего тела характеризует пропагатор ${U}/$.
• Сегмент $B\rightarrow C$ При намагничивании или адиабатическом сжатии внешнее поле изменяется, расширяя щель между уровнями энергии гамильтониана. Динамику характеризует пропагатор ${U}_{\text{ch}}$.
• Сегмент $C\rightarrow D$ изомагнитный или изохорный процесс частичного равновесия с горячей ванной, описываемый пропагатором $U_{\text{h}}$.
• Сегмент $D\rightarrow A$ размагничивание или адиабатическое расширение, уменьшающее энергетические щели в гамильтониане, характеризуемом пропагатором $U_{\text{hc}}$.

Распространитель четырехтактного цикла становится $U_{\text{global}}$, который является упорядоченным произведением распространителей сегментов:

${U}_{\text{global}}~~=~~{U}_{\text{hc}}{U}_{\text{h}}{U}_{\text{ch}}{U}_{\text{c}}$

Пропагаторы представляют собой линейные операторы, определенные в векторном пространстве, которое полностью определяет состояние рабочей среды. Как и во всех термодинамических циклах, пропагаторы последовательных сегментов не коммутируют. $[{\ U}_{i},{U}_{j}]\neq 0$. Коммутирующие пропагаторы приведут к нулевой мощности.

В возвратно-поступательном квантовом тепловом двигателе рабочим телом является квантовая система, такая как спиновые системы. или гармонический генератор. Для достижения максимальной мощности время цикла должно быть оптимизировано. В поршневом холодильнике есть две основные временные шкалы: время цикла. $\tau _{\text{cyc}}$ и внутренний временной масштаб $2\pi /\omega$. В общем, когда $\tau _{\text{cyc}}\gg 2\pi /\omega$ тот Двигатель работает в квазиадиабатических условиях. Единственный квантовый эффект можно обнаружить при низких температурах. где единица энергии устройства становится $\hbar \omega$ вместо $k_{\text{B}}T$. Эффективность в этом пределе $\eta =1-{\frac {\omega _{\text{c}}}{\omega _{\text{h}}}}$, всегда меньше эффективности Карно $\eta _{\text{c}}$. При высокой температуре и для гармонического рабочего тела КПД при максимальной мощности становится $\eta =1-{\sqrt {\frac {T_{\text{c}}}{T_{\text{h}}}}}$ что является эндообратимым результатом термодинамики .

При более коротких временах цикла рабочее тело не может адиабатически следовать за изменением внешнего параметра. Это приводит к явлениям, подобным трению. Для ускорения работы системы требуется дополнительная мощность. Признаком такой динамики является развитие когерентности, вызывающей дополнительную диссипацию. Удивительно, но динамика, приводящая к трению, квантована, а это означает, что решения адиабатического расширения /сжатия без трения можно найти за конечное время. В результате оптимизацию приходится проводить только в отношении выделенного времени. для обогрева транспорта. В этом режиме квантовая особенность когерентности ухудшает производительность. Оптимальная производительность без трения достигается, когда когерентность можно отменить.

Кратчайшие сроки цикла $\tau _{\text{cyc}}\ll 2\pi /\omega$, иногда называемые внезапными циклами, обладают универсальными свойствами. В этом случае когерентность способствует увеличению мощности цикла.

квантовый цикл двухтактного двигателя, эквивалентный циклу Отто, на основе двух кубитов Предложен . Первый кубит имеет частоту $\omega _{\text{h}}$ и второй $\omega _{\text{c}}$. Цикл состоит из первого этапа частичного уравновешивания двух кубитов с параллельной горячей и холодной ванной. Второй такт мощности состоит из частичной или полной замены между кубитами. Операция обмена генерируется унитарным преобразованием, сохраняющим энтропию. в результате это чистый силовой удар.

Холодильники с квантовым циклом Отто имеют тот же цикл, что и магнитное охлаждение .

Непрерывные квантовые двигатели

Квантовые двигатели непрерывного действия являются квантовыми аналогами турбин . Механизм вывода работы связан с внешним периодическим полем, обычно с электромагнитным полем. Таким образом, тепловая машина является моделью лазера . Модели различаются выбором рабочего вещества. и источник и сток тепла. Двухуровневый с внешним приводом, три уровня четырехуровневый и связанные гармонические осцилляторы были изучены.

Периодическое возбуждение расщепляет структуру энергетических уровней рабочего тела. Это разделение позволяет двухуровневому движку соединяться. выборочно к горячим и холодным ваннам и выработке энергии. С другой стороны, игнорирование этого расщепления при выводе уравнения движения нарушит второй закон термодинамики .

Нетермические виды топлива рассматривались для квантовых тепловых двигателей. Идея состоит в том, чтобы увеличить энергетическую ценность горячей ванны без увеличивая его энтропию. Этого можно достичь, используя согласованность или отжатая термальная ванна. Эти устройства не нарушают второй закон термодинамики.

Эквивалентность тепловых машин возвратно-поступательного и непрерывного действия в квантовом режиме

Двухтактные, четырехтактные и машины непрерывного действия сильно отличаются друг от друга. Однако было показано что существует квантовый режим, в котором все эти машины становятся термодинамически эквивалентными друг другу. Хотя внутрицикловая динамика в режиме эквивалентности сильно различается в разных типах двигателей, когда цикл завершается, все они выполняют одинаковый объем работы и потребляют одинаковое количество тепла (следовательно, они также имеют один и тот же КПД). . Эта эквивалентность связана с когерентным механизмом извлечения работы и не имеет классического аналога. Эти квантовые особенности были продемонстрированы экспериментально.

Тепловые двигатели и открытые квантовые системы

Простейший пример работает в условиях квазиравновесия. Его главной квантовой особенностью является дискретная структура энергетических уровней. Более реалистичные устройства работают вне равновесия, обладая фрикционными утечками тепла и конечным тепловым потоком. Квантовая термодинамика предлагает динамическую теорию, необходимую для систем, находящихся вне равновесия, таких как тепловые двигатели. включение динамики в термодинамику. Теория открытых квантовых систем составляет основную теорию. Для тепловых двигателей сокращенное описание динамики Рабочее вещество ищут, отслеживая горячие и холодные ванны. Отправной точкой является общий гамильтониан объединенных систем:

$H=H_{\text{s}}s+H_{\text{c}}+H_{\text{h}}{\text{h}}+H_{\text{sc}}+H_{\text{sh}}$

и системный гамильтониан $H_{\text{s}}(t)$ зависит от времени. Сокращенное описание приводит к уравнению движения системы:

${\frac {d}{dt}}\rho =-{\frac {i}{\hbar }}[H_{\text{s}},\rho ]+L_{\text{h}}(\rho )+L_{\text{c}}(\rho )$

где $\rho$ – оператор плотности, описывающий состояние рабочего тела и $L_{\text{h/c}}$ является генератором диссипативной динамики включающий в себя условия теплоотдачи от ванн. Используя эту конструкцию, общее изменение энергии подсистемы становится:

${\frac {d}{dt}}E=\left\langle {\frac {\partial H_{\text{s}}}{\partial t}}\right\rangle +\langle L_{\text{h}}(H_{\text{s}})\rangle +\langle L_{\text{c}}(H_{\text{s}})\rangle$

что приводит к динамической версии первого закона термодинамики :

• Сила $P=\left\langle {\frac {\partial H}{\partial t}}\right\rangle$
• Тепловые потоки $J_{\text{h}}=\langle L_{\text{h}}(H_{\text{s}})\rangle$ и $J_{\text{c}}=\langle L_{\text{c}}(H_{\text{s}})\rangle$.

Скорость производства энтропии становится:

${\frac {dS}{dt}}=-{\frac {J_{\text{h}}}{T_{\text{h}}}}-{\frac {J_{\text{c}}}{T_{\text{c}}}}\geq 0$

Глобальная структура квантовой механики отражена в выводе сокращенного описания. Вывод, соответствующий законам термодинамики, основан на предел слабой связи. Термодинамическая идеализация предполагает, что система и ванны некоррелированы, а это означает, что общее состояние объединенной системы всегда становится тензорным произведением:

$\rho =\rho _{\text{s}}\otimes \rho _{\text{h}}\otimes \rho _{\text{c}}~.$

В этих условиях динамические уравнения движения принимают вид: ${\frac {d}{dt}}\rho _{\text{s}}={L}\rho _{\text{s}}~,$ где ${L}$ - супероператор Лиувилля, описываемый в терминах гильбертова пространства системы, где резервуары описаны неявно. В формализме квантовой открытой системы $L$ может принять форму генератор Горини-Коссаковского-Сударшана-Линдблада (ГКС-Л) Марковский , также известный как уравнение Линдблада . Были предложены теории, выходящие за рамки режима слабой связи.

Квантовый абсорбционный холодильник

Абсорбционный холодильник имеет уникальное значение при создании автономного квантового устройства. Такое устройство не требует внешнего питания и работает без внешнего вмешательства в планирование операций. . Базовая конструкция включает три ванны; энергетическая ванна, горячая ванна и холодная ванна. Модель трехколесного велосипеда является шаблоном для абсорбционного холодильника.

Абсорбционный трехколесный холодильник Quantum. Устройство состоит из трех ванн, в которых $T_{\text{d}}\geq T_{\text{h}}\geq T_{\text{c}}$. Тепло передается от накопителя энергии и холодной ванны к горячей ванне.

Трехколесный двигатель имеет типовую конструкцию. Базовая модель состоит из трех термальных ванн: Горячая ванна с температурой $T_{\text{h}}$, холодная ванна с температурой $T_{\text{c}}$ и рабочая ванна с температурой $T_{\text{d}}$.

Каждая ванна подключена к двигателю через частотный фильтр, который можно моделировать тремя генераторами:

$H_{0}=\hbar \omega _{\text{h}}a^{\dagger }a+\hbar \omega _{\text{c}}b^{\dagger }b+\hbar \omega _{\text{d}}c^{\dagger }c~~,$

где $\omega _{\text{h}}$, $\omega _{\text{c}}$ и $\omega _{\text{d}}$ частоты фильтра на резонансе $\omega _{\text{d}}=\omega _{\text{h}}-\omega _{\text{c}}$.

Устройство работает как холодильник, снимая возбуждение как с холодной ванны, так и с рабочей ванны. и создание возбуждения в горячей ванне. Термин $a^{\dagger }bc$ в гамильтониане нелинейно и имеет решающее значение для двигателя или холодильника.

$H_{I}=\hbar \epsilon \left(ab^{\dagger }c^{\dagger }+a^{\dagger }bc\right)~~,$

где $\epsilon$ это сила сцепления.

Первый закон термодинамики представляет собой энергетический баланс тепловых потоков, исходящих из трех ванн и коллимирующихся в системе:

${\frac {dE_{\text{s}}}{dt}}={J}_{\text{h}}+{J}_{\text{c}}+{J}_{\text{d}}~~.$

В установившемся режиме в трехколесном велосипеде не накапливается тепло, поэтому ${\frac {dE_{\text{s}}}{dt}}=0$. Кроме того, в установившемся режиме энтропия генерируется только в ваннах, что приводит к второму закону термодинамики :

${\frac {d}{dt}}\Delta {S}_{\text{u}}~=~-{\frac {{J}_{\text{h}}}{T_{\text{h}}}}-{\frac {{J}_{\text{c}}}{T_{\text{c}}}}-{\frac {{J}_{\text{d}}}{T_{\text{d}}}}~\geq ~0~~.$

Эта версия второго закона является обобщением утверждения теоремы Клаузиуса ; тепло не переходит самопроизвольно от холодных тел к горячим. Когда температура $T_{\text{d}}\rightarrow \infty$энтропия в энергетической ванне не генерируется. Поток энергии без сопутствующего производства энтропии эквивалентен генерации чистой энергии: ${P}={J}_{\text{d}}$, где ${P}$ это выходная мощность.

Квантовые холодильники и третий закон термодинамики

По-видимому, существуют две независимые формулировки третьего закона термодинамики, обе первоначально были сформулированы Вальтером Нернстом . Первая формулировка известна как теорема о теплоте Нернста и может быть сформулирована как:

• Энтропия любого чистого вещества, находящегося в термодинамическом равновесии, приближается к нулю, когда температура приближается к нулю.

Вторая формулировка является динамической и известна как принцип недостижимости :

• Невозможно никакой процедурой, какой бы идеализированной она ни была, довести любую сборку до абсолютной нулевой температуры за конечное число операций.

В устойчивом состоянии второй закон термодинамики предполагает, что общее производство энтропии неотрицательно. Когда холодная ванна приближается к температуре абсолютного нуля, необходимо устранить расхождение производства энтропии на холодной стороне когда $T_{\text{c}}\rightarrow 0$, поэтому

${\dot {S}}_{\text{c}}\propto -T_{\text{c}}^{\alpha }~~~,~~~~\alpha \geq 0~~.$

Для $\alpha =0$ выполнение второго закона зависит от производства энтропии в других ваннах, что должно компенсировать отрицательное производство энтропии в холодной ванне. Первая формулировка третьего закона изменяет это ограничение. Вместо $\alpha \geq 0$ третий закон налагает $\alpha >0$, гарантируя, что при абсолютном нуле производство энтропии в холодной ванне равно нулю: ${\dot {S}}_{\text{c}}=0$. Это требование приводит к условию масштабирования теплового тока ${J}_{\text{c}}\propto T_{\text{c}}^{\alpha +1}$.

Вторую формулировку, известную как принцип недостижимости, можно перефразировать так:

• Ни один холодильник не может охладить систему до абсолютной нулевой температуры за конечное время.

Динамика процесса охлаждения определяется уравнением

${J}_{\text{c}}(T_{\text{c}}(t))=-c_{V}(T_{\text{c}}(t)){\frac {dT_{\text{c}}(t)}{dt}}~~.$

где $c_{V}(T_{\text{c}})$ – теплоемкость ванны. принимая ${J}_{\text{c}}\propto T_{\text{c}}^{\alpha +1}$ и $c_{V}\sim T_{\text{c}}^{\eta }$ с ${\eta }\geq 0$, мы можем количественно оценить эту формулировку, оценив характеристический показатель степени $\zeta$ процесса охлаждения,

${\frac {dT_{\text{c}}(t)}{dt}}\propto -T_{\text{c}}^{\zeta },~~~~~T_{\text{c}}\rightarrow 0,~~~~~{\zeta =\alpha -\eta +1}$

Это уравнение вводит связь между характеристическими показателями $\zeta$ и $\alpha$. Когда $\zeta <0$ тогда ванна охлаждается до нулевой температуры за конечное время, что влечет за собой нарушение третьего закона. Из последнего уравнения видно, что принцип недостижимости является более ограничительным, чем теорема о теплоте Нернста .

Дальнейшее чтение

Деффнер, Себастьян и Кэмпбелл, Стив. «Квантовая термодинамика: введение в термодинамику квантовой информации» (Morgan & Claypool Publishers, 2019).

Ф. Биндер, Л. А. Корреа, К. Гоголин, Дж. Андерс, Г. Адессо (ред.) «Термодинамика в квантовом режиме. Фундаментальные аспекты и новые направления». (Весна 2018 г.)

Геммер, Йохен, М. Мишель и Гюнтер Малер. «Квантовая термодинамика. Возникновение термодинамического поведения в составных квантовых системах. 2». (2009).

Петруччионе, Франческо и Хайнц-Петер Брейер. Теория открытых квантовых систем. Издательство Оксфордского университета, 2002.

Внешние ссылки

• «Наномасштабный тепловой двигатель превышает стандартный предел эффективности» . физ.орг .