Кинжал компактной категории

В теории категорий , разделе математики , кинжально-компактные категории (или кинжально-компактные замкнутые категории ) впервые появились в 1989 году в работе Серджио Допличера и Джона Э. Робертса о реконструкции компактных топологических групп из их категории конечномерных непрерывных унитарных групп. представления (то есть категории Таннака ). Они также появились в работах Джона Баэза и Джеймса Долана как пример полустрогих k -кратно моноидальных n -категорий , которые описывают общие топологические квантовые теории поля . для n = 1 и k = 3. Они представляют собой фундаментальную структуру Абрамского и Боба Кука Самсона категорической квантовой механики .

Обзор

Компактные категории кинжала могут использоваться для выражения и проверки некоторых фундаментальных квантовой информации протоколов , а именно: телепортации , телепортации логических вентилей и замены запутанности , а также стандартных понятий, таких как унитарность, внутренний продукт, след, двойственность Чоя-Джамиолковского , полная позитивность , утверждает Белл. и многие другие понятия описываются языком компактных категорий кинжала. Все это следует из приведенной ниже теоремы о полноте. Категориальная квантовая механика использует компактные категории кинжала в качестве фоновой структуры, относительно которой могут быть абстрактно определены другие квантовомеханические понятия, такие как квантовые наблюдаемые и их дополнительность. Это формирует основу для высокоуровневого подхода к квантовой обработке информации .

Формальное определение

— Компактная категория кинжала это симметричная моноидальная категория кинжала. $\mathbf {C}$ который также является компактно-закрытым , вместе с отношением, связывающим структуру кинжала с компактной структурой. Конкретно крестик используется для соединения блока с блоком, так что для всех $A$ в $\mathbf {C}$, коммутирует следующая диаграмма:

Dagger Compact Category

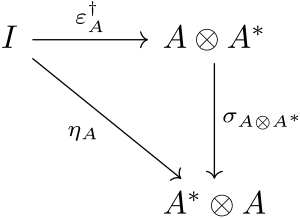
Подводя итог всем этим пунктам:

• Категория является замкнутой , если она имеет внутренний функтор hom ; то есть, если hom-множество морфизмов между двумя объектами категории является объектом самой категории (а не Set ).
• Категория называется моноидальной , если она снабжена ассоциативным бифунктором. $\mathbf {C} \otimes \mathbf {C} \to \mathbf {C}$ который ассоциативен, естественен и имеет левые и правые идентичности, подчиняющиеся определенным условиям связности .
• Моноидальная категория называется симметричной моноидальной , если для каждой пары A , B объектов из C существует изоморфизм $\sigma _{A,B}:A\otimes B\simeq B\otimes A$ это естественно как для A , так и для B и, опять же, подчиняется определенным условиям когерентности ( категории симметричной моноидации ). подробности см. в
• Моноидальная категория называется компактно-замкнутой , если каждый объект $A\in \mathbf {C}$ имеет двойной объект $A^{*}$. Категории с двойственными объектами снабжены двумя морфизмами: единицей $\eta _{A}:I\to A^{*}\otimes A$ и единица $\varepsilon _{A}:A\otimes A^{*}\to I$, которые удовлетворяют определенным условиям связности или дергания.
• Категория является кинжальной категорией, если она оснащена инволютивным функтором. $\dagger \colon \mathbf {C} ^{op}\rightarrow \mathbf {C}$ это тождество объектов, но оно отображает морфизмы на сопряженные с ними объекты.
• Моноидальная категория является кинжало-симметричной, если она является кинжалной категорией, симметрична и имеет условия когерентности, которые делают различные функторы естественными.

Компактная категория кинжала тогда является категорией, которая является каждой из вышеперечисленных и, кроме того, имеет условие, связывающее структуру кинжала с компактной структурой. Это делается путем привязки единицы к единице с помощью кинжала:

$\sigma _{A,A^{*}}\circ \varepsilon _{A}^{\dagger }=\eta _{A}$

показано на схеме передвижения выше. В категории FdHilb конечномерных гильбертовых пространств это последнее условие можно понимать как определение кинжала (эрмитова сопряженного) как транспонированного комплексно-сопряженного.

Примеры

Следующие категории относятся к компактным кинжалам.

• Категория FdHilb конечномерных гильбертовых пространств и линейных отображений . Морфизмы представляют собой линейные операторы между гильбертовыми пространствами. Произведение — обычное тензорное произведение , а кинжал здесь — эрмитово сопряжение .
• Категория Rel множеств и отношений . Произведение, конечно же, является декартовым произведением . Кинжал здесь как раз наоборот .
• Категория конечно порожденных проективных модулей над коммутативным кольцом . Кинжал здесь — это просто транспонирование матрицы .
• Категория nCob кобордизмов ​ . Здесь n-мерные кобордизмы — это морфизмы, дизъюнктное объединение — это тензор, а обращение объектов (замкнутые многообразия) — это кинжал. Топологическую квантовую теорию поля можно определить как функтор из nCob в FdHilb .
• Категория Span ( C ) промежутков для любой категории C с конечными пределами .

Бесконечномерные гильбертовы пространства не являются кинжально-компактными и описываются кинжально-симметричными моноидальными категориями .

Структурные теоремы

Селинджер показал, что компактные категории кинжала допускают диаграммный язык в стиле Джойал-Стрита. и доказал, что кинжальные компактные категории полны относительно конечномерных гильбертовых пространств. т. е. эквациональное утверждение на языке компактных категорий кинжала справедливо тогда и только тогда, когда оно может быть получено в конкретной категории конечномерных гильбертовых пространств и линейных отображений. не существует Аналогичной полноты для Rel или nCob .

Из этого результата о полноте следует, что на эту категорию распространяются различные теоремы из гильбертовых пространств. Например, теорема о запрете клонирования подразумевает, что не существует универсального морфизма клонирования. Полнота также подразумевает гораздо более приземленные особенности: компактные категории кинжала могут иметь базис так же, как может иметь базис гильбертово пространство. Операторы можно разложить по базису; операторы могут иметь собственные векторы и т. д . Это рассматривается в следующем разделе.

Основа

Теорема о полноте подразумевает, что основные понятия из гильбертовых пространств переносятся на любую категорию компактных кинжалов. Однако используемый типичный язык меняется. Понятие базиса дается в терминах коалгебры . Учитывая объект A из категории компактов кинжала, базисом является комоноидный объект. $(A,\delta ,\varepsilon )$. Этими двумя операциями являются копирование или коумножение δ: A → A ⊗ операция Кокоммутативный и коассоциативный морфизм и удаления или морфизм коединиц ε: A → I . Вместе они подчиняются пяти аксиомам:

Комультипликативность:

$(1_{A}\otimes \varepsilon )\circ \delta =1_{A}=(\varepsilon \otimes 1_{A})\circ \delta$

Коассоциативность:

$(1_{A}\otimes \delta )\circ \delta =(\delta \otimes 1_{A})\circ \delta$

Кокоммутативность:

$\sigma _{A,A}\circ \delta =\delta$

Изометрия:

$\delta ^{\dagger }\circ \delta =1_{A}$

Закон Фробениуса :

$(\delta ^{\dagger }\otimes 1_{A})\circ (1_{A}\otimes \delta )=\delta \circ \delta ^{\dagger }$

Чтобы увидеть, что эти отношения определяют базис векторного пространства в традиционном смысле, напишите коумножение и счетную единицу, используя обозначение скобки и понимая, что теперь это линейные операторы, действующие на векторы $|j\rangle$ в гильбертовом пространстве H :

${\begin{aligned}\delta :H&\to H\otimes H\\|j\rangle &\mapsto |j\rangle \otimes |j\rangle =|jj\rangle \\\end{aligned}}$

и

${\begin{aligned}\varepsilon :H&\to \mathbb {C} \\|j\rangle &\mapsto 1\\\end{aligned}}$

Единственные векторы $|j\rangle$ которые могут удовлетворять пяти вышеуказанным аксиомам, должны быть ортогональны друг другу; тогда единица однозначно определяет базис. Наводящие на размышления имена копирования и удаления для операторов коумножения и соединицы исходят из идеи, что теорема о запрете клонирования и теорема о запрете удаления утверждают, что единственные векторы, которые можно копировать или удалять, являются ортогональными базисными векторами.

Общие результаты

Учитывая приведенное выше определение базиса, можно сформулировать ряд результатов для гильбертовых пространств для компактных категорий кинжала. Ниже мы перечислим некоторые из них, взятые из если не указано иное.

• Базис также можно понимать как соответствующий наблюдаемому , в том смысле, что данная наблюдаемая влияет на (ортогональные) базисные векторы. То есть наблюдаемая представлена ​​объектом A вместе с двумя морфизмами, определяющими базис: $(A,\delta ,\varepsilon )$.
• Собственное состояние наблюдаемого $(A,\delta ,\varepsilon )$ какой-нибудь объект $\psi$ для чего

$\delta \circ \psi =\psi \otimes \psi$

Собственные состояния ортогональны друг другу.

• Объект $\psi$ дополняет наблюдаемое ​ $(A,\delta ,\varepsilon )$ если

$\delta ^{\dagger }\circ ({\overline {\psi }}\otimes \psi )=\varepsilon ^{\dagger }$

(В квантовой механике вектор состояния $\psi$ Говорят, что она дополняет наблюдаемую, если любой результат измерения равновероятен. а именно собственное состояние спина S _x равновероятно при измерении в базисе S _z , или собственные состояния импульса равновероятны при измерении в базисе положения.)

• Две наблюдаемые $(A,\delta _{X},\varepsilon _{X})$ и $(A,\delta _{Z},\varepsilon _{Z})$ дополняют друг друга, если

$\delta _{Z}^{\dagger }\circ \delta _{X}=\varepsilon _{Z}\circ \varepsilon _{X}^{\dagger }$

• Дополнительные объекты порождают унитарные преобразования . То есть,

$\delta ^{\dagger }\circ (\psi \otimes 1_{A})$

унитарно тогда и только тогда, когда $\psi$ является дополнением к наблюдаемому $(A,\delta ,\varepsilon )$

Ссылки

• Категория «Кинжал-компакт» в n Lab