Двойной объект

В теории категорий , разделе математики , двойственный объект является аналогом двойственного векторного пространства из линейной алгебры для объектов в произвольных моноидальных категориях . Это лишь частичное обобщение, основанное на категориальных свойствах двойственности конечномерных пространств векторных . Объект, допускающий двойственный объект, называется дуализируемым объектом . В этом формализме бесконечномерные векторные пространства не дуализуемы, поскольку двойственное векторное пространство V ^∗ не удовлетворяет аксиомам. ^[1] Часто объект является дуализируемым только тогда, когда он удовлетворяет некоторому свойству конечности или компактности . ^[2]

Категория , в которой каждый объект имеет двойник, называется автономной или жесткой . Категория конечномерных векторных пространств со стандартным тензорным произведением является жесткой, а категория всех векторных пространств - нет.

Мотивация

Пусть V конечномерное векторное пространство над некоторым полем K. — Стандартное понятие двойственного векторного пространства V ^∗ обладает следующим свойством: для любых K -векторных пространств U и W существует присоединение Hom _K ( U ⊗ V , W ) = Hom _K ( U , V ^∗ ⊗ W ), и это характеризует V ^∗ с точностью до единственного изоморфизма . Это выражение имеет смысл в любой категории с соответствующей заменой тензорного произведения векторных пространств. Для любой моноидальной категории ( C , ⊗) можно попытаться определить двойственный объект V как объект V ^∗ ∈ C с изоморфизмом бифункторов естественным

Hom _C ((–) ₁ ⊗ V , (–) ₂ ) → Hom _C ((–) ₁ , V ^∗ ⊗ (–) ₂)

Для корректного представления о двойственности это отображение должно быть не только естественным в смысле теории категорий, но и каким-то образом соответствовать моноидальной структуре. ^[1] Таким образом, фактическое определение двойственного объекта является более сложным.

В замкнутой моноидальной категории C , т.е. моноидальной категории с внутренним функтором Hom , альтернативным подходом является моделирование стандартного определения двойственного векторного пространства как пространства функционалов . Для объекта V ∈ C определим V ^∗ быть ${\underline {\mathrm {Hom} }}_{C}(V,\mathbb {1} _{C})$ , где 1 _C — моноидальное тождество. В некоторых случаях этот объект будет двойным объектом по отношению к V в указанном выше смысле, но в целом это ведет к другой теории. ^[3]

Определение

Рассмотрим объект $X$ в моноидальной категории $(\mathbf {C} ,\otimes ,I,\alpha ,\lambda ,\rho )$ . Объект $X^{*}$ называется левым двойственным $X$ если существуют два морфизма

\eta :I\to X\otimes X^{*}

, называемая кооценкой , и

\varepsilon :X^{*}\otimes X\to I

, называемая оценкой ,

такие, что следующие две диаграммы коммутируют:

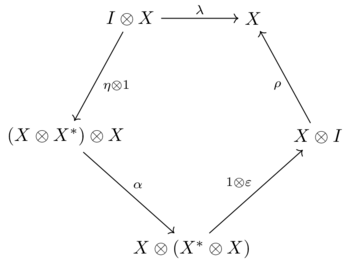и

Объект $X$ называется правым двойственным $X^{*}$ . Это определение принадлежит Dold & Puppe (1980) .

Левые двойственные числа канонически изоморфны, если они существуют, как и правые двойственные числа. Когда C сплетенный симметричный (или ), каждый левый дуальный является также правым дуальным , и наоборот.

Если рассматривать моноидальную категорию как бикатегорию с одним объектом, двойственная пара — это в точности присоединенная пара .

Примеры

Рассмотрим моноидальную категорию (Vect _K , ⊗ _K ) векторных пространств над полем K со стандартным тензорным произведением. Пространство V дуализуемо тогда и только тогда, когда оно конечномерно, и в этом случае двойственный объект V ^∗ совпадает со стандартным понятием двойственного векторного пространства .
Рассмотрим моноидальную категорию (Mod _R , ⊗ _R ) модулей над коммутативным кольцом R со стандартным тензорным произведением . Модуль M дуализируем тогда и только тогда, когда он является конечно порожденным проективным модулем . В этом случае двойственный объект M ^∗ также задается модулем гомоморфизмов Hom _R ( M , R ).
Рассмотрим гомотопическую категорию спектров точечных смэш - Ho(Sp) со произведением в качестве моноидальной структуры. Если M — компактный ретракт окрестностей в $\mathbb {R} ^{n}$ (например, компактное гладкое многообразие ), то соответствующий точечный спектр Σ ^∞( М ⁺) дуализируемо. Это следствие двойственности Спанье–Уайтхеда , из которой, в частности, следует двойственность Пуанкаре для компактных многообразий. ^[1]
Категория $\mathrm {End} (\mathbf {C} )$ эндофункторов категории $\mathbf {C}$ является моноидальной категорией относительно композиции функторов . Функтор $F$ является левым двойственным функтором $G$ тогда и только тогда, когда $F$ остается присоединенным к $G$ . ^[4]

Категории с двойниками

Моноидальную категорию, в которой каждый объект имеет левый (соответственно правый) двойственный, иногда называют левой (соответственно правой) автономной категорией. Алгебраические геометры называют ее левой (соответственно правой) жесткой категорией . Моноидальная категория, в которой каждый объект имеет как левый, так и правый двойственный объект, называется автономной категорией . Автономная категория, которая также является симметричной, называется компактной замкнутой категорией .

Следы

Любой эндоморфизм f дуализируемого объекта допускает след , который является некоторым эндоморфизмом моноидальной единицы C . В качестве особых случаев это понятие включает след в линейной алгебре и эйлерову характеристику цепного комплекса .

См. также

Дуализирующий объект

Ссылки

^ Jump up to: ^а ^б ^с Понто, Кейт; Шульман, Майкл (2014). «Следы в симметричных моноидальных категориях» . Математические изложения . 32 (3): 248–273. arXiv : 1107.6032 . Бибкод : 2011arXiv1107.6032P . дои : 10.1016/j.exmath.2013.12.003 .
^ Беккер, Джеймс С.; Готлиб, Дэниел Генри (1999). «История двойственности в алгебраической топологии» (PDF) . В Джеймсе, И.М. (ред.). История топологии . Северная Голландия. стр. 725–745. ISBN 978-0-444-82375-5 .
^ двойной объект в закрытой категории в n Lab
^ См., например Никшич, Д.; Этингоф, ИП ; Гелаки, С.; Острик, В. (2016). «Упражнение 2.10.4». Тензорные категории . Математические обзоры и монографии. Том. 205. Американское математическое общество. п. 41. ИСБН 978-1-4704-3441-0 .

Дольд, Альбрехт ; Пуппе, Дитер (1980), «Двойственность, след и перенос», Труды Международной конференции по геометрической топологии (Варшава, 1978) , PWN-Polish Scientific Publishers, стр. 81–102, ISBN 9788301017873 , МР 0656721 , OCLC 681088710
Фрейд, Питер ; Йеттер, Дэвид (1989). «Плетеные компактные закрытые категории с приложениями к низкомерной топологии» . Достижения в математике . 77 (2): 156–182. дои : 10.1016/0001-8708(89)90018-2 .
Джоял, Андре ; Стрит, Росс . «Геометрия тензорного исчисления II» (PDF) . Синтезирующая библиотека . 259 : 29–68. CiteSeerX 10.1.1.532.1533 .

Эта теории категорий статья, посвященная , незавершена . Вы можете помочь Википедии, расширив ее .

[traces-1] Jump up to: ^а ^б ^с Понто, Кейт; Шульман, Майкл (2014). «Следы в симметричных моноидальных категориях» . Математические изложения . 32 (3): 248–273. arXiv : 1107.6032 . Бибкод : 2011arXiv1107.6032P . дои : 10.1016/j.exmath.2013.12.003 .

[2] Беккер, Джеймс С.; Готлиб, Дэниел Генри (1999). «История двойственности в алгебраической топологии» (PDF) . В Джеймсе, И.М. (ред.). История топологии . Северная Голландия. стр. 725–745. ISBN 978-0-444-82375-5 .

[3] двойной объект в закрытой категории в n Lab

[4] См., например Никшич, Д.; Этингоф, ИП ; Гелаки, С.; Острик, В. (2016). «Упражнение 2.10.4». Тензорные категории . Математические обзоры и монографии. Том. 205. Американское математическое общество. п. 41. ИСБН 978-1-4704-3441-0 .

[1]

[2]

[3]

[4]