Параллакс в астрономии
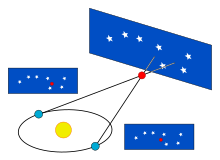

Наиболее важные фундаментальные измерения расстояний в астрономии основаны на тригонометрическом параллаксе , применяемом в методе звездного параллакса . По мере того как Земля вращается вокруг Солнца, положение ближайших звезд будет немного смещаться на более отдаленном фоне. Эти сдвиги представляют собой углы в равнобедренном треугольнике , где 2 а.е. (расстояние между крайними положениями орбиты Земли вокруг Солнца) составляют базовую часть треугольника, а расстояние до звезды представляет собой длинные катеты равной длины. Величина смещения довольно мала даже для ближайших звезд: она составляет 1 угловую секунду для объекта на расстоянии 1 парсек (3,26 светового года ), а затем уменьшается по угловой величине по мере увеличения расстояния. Астрономы обычно выражают расстояния в парсеках ( угловых секундах параллакса); световые годы используются в популярных средствах массовой информации.
в несколько раз Поскольку параллакс становится меньше с увеличением расстояния до звезды, полезные расстояния можно измерить только для звезд, которые находятся достаточно близко, чтобы иметь параллакс, превышающий точность измерения . В 1990-е годы, например, миссия Hipparcos получила параллаксы более ста тысяч звезд с точностью около миллисекунды дуги . [1] обеспечивая полезные расстояния для звезд до нескольких сотен парсеков. может космического телескопа Хаббл потенциально Широкоугольная камера 3 обеспечить точность от 20 до 40 угловых микросекунд, что позволяет надежно измерять расстояния до 5000 парсеков (16 000 световых лет) для небольшого количества звезд. [2] [3] Космическая миссия «Гайя» предоставила столь же точные расстояния до большинства звезд ярче 15-й звездной величины. [4]
Расстояния могут быть измерены с точностью до 10% до Галактического центра , находящегося на расстоянии около 30 000 световых лет. Звезды имеют скорость относительно Солнца, которая вызывает собственное движение (поперечное по небу) и радиальную скорость (движение к Солнцу или от него). Первое определяется путем построения графика изменения положения звезд за многие годы, а второе - путем измерения доплеровского сдвига спектра звезды, вызванного движением вдоль луча зрения. Для группы звезд с одинаковым спектральным классом и схожим диапазоном звездных величин средний параллакс можно получить на основе статистического анализа собственных движений относительно их лучевых скоростей. Этот метод статистического параллакса полезен для измерения расстояний до ярких звезд размером более 50 парсек и гигантских переменных звезд , включая цефеиды и переменные RR Лиры . [5]


Движение Солнца в пространстве обеспечивает более длинную базовую линию, что повысит точность измерений параллакса, известного как вековой параллакс . Для звезд диска Млечного Пути это соответствует средней базовой линии 4 а.е. в год, а для звезд гало базовая линия составляет 40 а.е. в год. Через несколько десятилетий базовая линия может быть на порядки больше, чем базовая линия Земля-Солнце, используемая для традиционного параллакса. Однако вековой параллакс вносит более высокий уровень неопределенности, поскольку относительная скорость наблюдаемых звезд является дополнительным неизвестным. При применении к выборкам из нескольких звезд неопределенность можно уменьшить; неопределенность обратно пропорциональна квадратному корню из размера выборки. [8]
Параллакс движущегося скопления — это метод, при котором движения отдельных звезд в ближайшем звездном скоплении можно использовать для определения расстояния до скопления. Только рассеянные скопления находятся достаточно близко, чтобы этот метод мог оказаться полезным. В частности, расстояние, полученное для Гиад, исторически было важной ступенью на лестнице расстояний.
Для других отдельных объектов могут быть сделаны фундаментальные оценки расстояния при особых обстоятельствах. Если расширение газового облака, такого как остаток сверхновой или планетарная туманность , можно наблюдать с течением времени, то параллакса расширения можно оценить расстояние до этого облака. Однако эти измерения страдают от неточностей в отклонении объекта от сферичности. Расстояние до двойных звезд , которые являются как визуальными , так и спектроскопическими двойными, также может быть оценено аналогичными способами, и они не страдают от вышеуказанной геометрической неопределенности. Общей характеристикой этих методов является то, что измерение углового движения сочетается с измерением абсолютной скорости (обычно получаемой с помощью эффекта Доплера ). Оценка расстояния получается путем вычисления того, насколько далеко должен находиться объект, чтобы его наблюдаемая абсолютная скорость соответствовала наблюдаемому угловому движению.
В частности, параллакс расширения может дать фундаментальную оценку расстояния до очень далеких объектов, поскольку выбросы сверхновых имеют большие скорости расширения и большие размеры (по сравнению со звездами). Кроме того, их можно наблюдать с помощью радиоинтерферометров , которые могут измерять очень малые угловые движения. В совокупности они дают фундаментальные оценки расстояний до сверхновых в других галактиках. [9] Хотя такие случаи ценны, они довольно редки, поэтому они служат важной проверкой последовательности на лестнице дистанции, а не сами по себе как рабочая лошадка.
Парсек
[ редактировать ]
Парсек используемая (обозначение: пк) — единица длины, для измерения больших расстояний до астрономических объектов за пределами Солнечной системы , примерно равная 3,26 световых лет или 206 265 астрономических единиц (АЕ), то есть 30,9 триллиона километров (19,2 триллиона миль ). . [а] Единица парсек получается с использованием параллакса и тригонометрии и определяется как расстояние, на котором 1 а.е. стягивает угол в одну угловую секунду. [10] ( 1/3600 градуса ) . Ближайшая звезда, Проксима Центавра , находится на расстоянии около 1,3 парсека (4,2 светового года) от Солнца : с этого расстояния расстояние между Землей и Солнцем составляет чуть меньше 1/3600 одного градуса . обзора [11] Большинство звезд, видимых невооруженным глазом, находятся в пределах нескольких сотен парсеков от Солнца, самые далекие - на расстоянии нескольких тысяч парсеков, а Галактика Андромеды - на расстоянии более 700 000 парсеков. [12]
Слово парсек представляет собой словосочетание «параллакс в одну секунду» и было придумано британским астрономом Гербертом Холлом Тернером в 1913 году. [13] упростить астрономам расчеты астрономических расстояний на основе только необработанных данных наблюдений. Частично по этой причине эту единицу предпочитают в астрономии и астрофизике , хотя световой год по-прежнему занимает видное место в научно-популярных текстах и в обычном использовании. Хотя парсеки используются для более коротких расстояний внутри Млечного Пути , для более крупных масштабов Вселенной требуются кратные парсекам, включая килопарсеки (кпк) для более удаленных объектов внутри и вокруг Млечного Пути, мегапарсеки (Мпк) для средних расстояний и гигапарсеков (Гпк) для многих квазаров и самых далеких галактик.
В августе 2015 года Международный астрономический союз (МАС) принял Резолюцию B2, в которой, как часть определения стандартизированной шкалы абсолютных и видимых болометрических величин , упоминалось существующее четкое определение парсека как точно 648 000 / π а.е., или примерно 3,085 677 581 491 3673 × 10 16 метры (на основе определения астрономической единицы, принятого МАС 2012 г.). Это соответствует малоугловому определению парсека, встречающемуся во многих астрономических справочниках. [14] [15]Звездный параллакс
[ редактировать ]
Звездный параллакс, создаваемый относительным движением между Землей и звездой , в модели Коперника можно рассматривать как возникающий из-за орбиты Земли вокруг Солнца: кажется, что звезда движется только относительно более удаленных объектов на небе. В геостатической модели движение звезды должно было бы считаться реальным , когда звезда колеблется по небу относительно звезд на заднем плане.
Звездный параллакс чаще всего измеряется с использованием годового параллакса , определяемого как разница в положении звезды, если смотреть с Земли и Солнца, т.е. угол, образуемый звездой средним радиусом орбиты Земли вокруг Солнца. Парсек угловой (3,26 светового года ) определяется как расстояние, на котором годовой параллакс равен 1 секунде . Годовой параллакс обычно измеряется путем наблюдения за положением звезды в разное время года по мере движения Земли по своей орбите. Измерение годового параллакса стало первым надежным способом определения расстояний до ближайших звезд. Первые успешные измерения звездного параллакса были произведены Фридрихом Бесселем в 1838 году для звезды 61 Лебедя с помощью гелиометра . [16] Звездный параллакс остается стандартом для калибровки других методов измерения. Точные расчеты расстояния на основе звездного параллакса требуют измерения расстояния от Земли до Солнца, которое теперь основано на радиолокационном отражении от поверхностей планет. [17]
Углы, участвующие в этих расчетах, очень малы и поэтому их трудно измерить. Ближайшая к Солнцу звезда (и, следовательно, звезда с самым большим параллаксом), Проксима Центавра , имеет параллакс 0,7687 ± 0,0003 угловых секунд. [18] Этот угол приблизительно соответствует углу объекта диаметром 2 сантиметра, расположенного на расстоянии 5,3 километра.

Тот факт, что звездный параллакс был настолько мал, что в то время его невозможно было наблюдать, использовался в качестве главного научного аргумента против гелиоцентризма в раннем Новом времени. , ясно Из геометрии Евклида что этот эффект был бы необнаружим, если бы звезды находились достаточно далеко, но по разным причинам такие гигантские расстояния казались совершенно неправдоподобными: одним из Тихо принципиальных возражений против коперниканского гелиоцентризма было то, что он Если бы это было совместимо с отсутствием наблюдаемого звездного параллакса, между орбитой Сатурна (на тот момент самой далекой известной планеты) и восьмой сферой (неподвижными звездами) должна была бы существовать огромная и маловероятная пустота. [20]
В 1989 году спутник Hipparcos был запущен в первую очередь для получения улучшенных параллаксов и собственных движений более чем 100 000 близлежащих звезд, что в десять раз увеличило охват метода. Несмотря на это, Hipparcos смог измерить углы параллакса только для звезд, находящихся на расстоянии около 1600 световых лет , что составляет немногим более одного процента диаметра Галактики Млечный Путь . Европейского космического агентства , Миссия Gaia запущенная в декабре 2013 года, может измерять углы параллакса с точностью до 10 микросекунд дуги , таким образом картируя близлежащие звезды (и, возможно, планеты) на расстоянии десятков тысяч световых лет от Земли. [21] [22] В апреле 2014 года астрономы НАСА сообщили, что космический телескоп Хаббл с помощью пространственного сканирования может точно измерять расстояния до 10 000 световых лет, что в десять раз лучше, чем предыдущие измерения. [19]
Суточный параллакс
[ редактировать ]Суточный параллакс — это параллакс, который меняется в зависимости от вращения Земли или от разницы в местоположении на Земле. Луна и, в меньшей степени, планеты земной группы или астероиды, видимые с разных точек зрения на Земле (в один и тот же момент), могут казаться по-разному расположенными на фоне неподвижных звезд. [23] [24]
Суточный параллакс был использован Джоном Флемстидом в 1672 году для измерения расстояния до Марса в момент его противостояния и с помощью этого для оценки астрономической единицы и размера Солнечной системы . [25]
Лунный параллакс
[ редактировать ]Лунный параллакс (часто сокращенно от лунного горизонтального параллакса или лунного экваториального горизонтального параллакса ) представляет собой особый случай (дневного) параллакса: Луна, будучи ближайшим небесным телом, имеет на сегодняшний день самый большой максимальный параллакс среди всех небесных тел, иногда превышающий 1 градус. [26]
Диаграмма звездного параллакса может также иллюстрировать лунный параллакс, если ее уменьшить и слегка изменить. Вместо «около звезды» читайте «Луна», и вместо круга внизу диаграммы, обозначающего размер орбиты Земли вокруг Солнца, примите его за размер земного шара, а круг вокруг поверхности Земли. Тогда лунный (горизонтальный) параллакс представляет собой разницу в угловом положении Луны относительно фона далеких звезд, если смотреть с двух разных точек зрения на Земле.
Одна из смотровых позиций — это место, с которого в данный момент Луну можно увидеть прямо над головой. То есть если смотреть вдоль вертикальной линии на диаграмме. Другая позиция просмотра — это место, откуда в тот же момент можно увидеть Луну на горизонте. То есть, если смотреть вдоль одной из диагональных линий, с позиции на поверхности Земли, примерно соответствующей одной из синих точек на модифицированной диаграмме.
Лунный (горизонтальный) параллакс альтернативно можно определить как угол, образующий на расстоянии Луны радиус Земли. [27] [28] - равен углу p на диаграмме в уменьшенном масштабе и изменении, как указано выше.
Лунный горизонтальный параллакс в любой момент времени зависит от линейного расстояния Луны от Земли. Линейное расстояние Земля-Луна постоянно меняется по мере того, как Луна движется по своей возмущенной и приблизительно эллиптической орбите вокруг Земли. Диапазон изменения линейного расстояния составляет примерно от 56 до 63,7 земных радиусов, что соответствует горизонтальному параллаксу примерно в градус дуги, но в пределах от примерно 61,4' до примерно 54'. [26] В «Астрономическом альманахе» и подобных публикациях для удобства астрономов (и астрономических навигаторов) периодически, например ежедневно, для удобства астрономов (и астрономических навигаторов) заносятся в таблицы лунный горизонтальный параллакс и/или линейное расстояние Луны от Земли, а также изучается, как эта координата меняется в зависимости от время является частью лунной теории .

Параллакс также можно использовать для определения расстояния до Луны .
Один из способов определить лунный параллакс из одного места — использовать лунное затмение. Полная тень Земли на Луне имеет видимый радиус кривизны, равный разнице между видимыми радиусами Земли и Солнца, видимыми с Луны. Можно видеть, что этот радиус равен 0,75 градуса, откуда (при видимом радиусе Солнца 0,25 градуса) мы получаем видимый радиус Земли 1 градус. Это дает для расстояния Земля-Луна 60,27 земного радиуса или 384 399 километров (238 854 миль). Эту процедуру впервые использовал Аристарх Самосский . [29] и Гиппарха , а позже проникла в творчество Птолемея . [30]
На диаграмме справа показано, как возникает ежедневный лунный параллакс на геоцентрической и геостатической модели планеты, в которой Земля находится в центре планетной системы и не вращается. Это также иллюстрирует тот важный момент, что параллакс не обязательно должен быть вызван каким-либо движением наблюдателя, вопреки некоторым определениям параллакса, которые утверждают, что это так, но может возникнуть исключительно из-за движения наблюдаемого.
Другой метод — сделать два снимка Луны одновременно из двух мест на Земле и сравнить положения Луны относительно звезд. Используя ориентацию Земли, эти два измерения положения и расстояние между двумя точками на Земле, можно триангулировать расстояние до Луны:

Об этом методе упоминает Жюль Верн в своем романе 1865 года «С Земли на Луну» :
До этого многие люди понятия не имели, как можно рассчитать расстояние, отделяющее Луну от Земли. Это обстоятельство было использовано, чтобы научить их тому, что это расстояние было получено путем измерения параллакса Луны. Если слово «параллакс» их удивляло, им говорили, что это угол, образованный двумя прямыми линиями, идущими от обоих концов радиуса Земли к Луне. Если у них возникали сомнения в совершенстве этого метода, им немедленно показывали, что это среднее расстояние не только составляет целых двести тридцать четыре тысячи триста сорок семь миль (94 330 лье), но и что астрономы не были ошибка более чем на семьдесят миль (≈ 30 лиг).
Солнечный параллакс
[ редактировать ]После того, как Коперник предложил свою гелиоцентрическую систему , в которой Земля вращается вокруг Солнца, стало возможным построить модель всей Солнечной системы без масштаба. Чтобы определить масштаб, необходимо измерить только одно расстояние внутри Солнечной системы, например, среднее расстояние от Земли до Солнца (теперь оно называется астрономической единицей , или АЕ). Когда это найдено с помощью триангуляции , это называется солнечным параллаксом , разницей в положении Солнца, если смотреть из центра Земли и точки на расстоянии одного радиуса Земли, то есть угол, образуемый на Солнце средним радиусом Земли. Знание солнечного параллакса и среднего радиуса Земли позволяет вычислить АС, что является первым небольшим шагом на долгом пути установления размера и возраста расширения. [31] видимой Вселенной.
Примитивный способ определения расстояния до Солнца через расстояние до Луны был предложен уже Аристархом Самосским в его книге «О размерах и расстояниях Солнца и Луны» . Он отметил, что Солнце, Луна и Земля образуют прямоугольный треугольник (с прямым углом к Луне) в момент первой или последней четверти Луны . Затем он подсчитал, что угол Луна-Земля-Солнце составляет 87°. Используя правильную геометрию , но неточные данные наблюдений, Аристарх пришел к выводу, что Солнце находится чуть менее чем в 20 раз дальше, чем Луна. Истинное значение этого угла близко к 89°50', а Солнце находится примерно в 390 раз дальше. [29]
Аристарх указывал, что Луна и Солнце имеют почти равные видимые угловые размеры , и поэтому их диаметры должны быть пропорциональны их расстояниям от Земли. Таким образом, он пришел к выводу, что Солнце примерно в 20 раз больше Луны. Этот вывод хотя и неверен, но логически вытекает из его неверных данных. Это предполагает, что Солнце больше Земли, что может служить подтверждением гелиоцентрической модели. [32]

Хотя результаты Аристарха были неверными из-за ошибок наблюдений, они были основаны на правильных геометрических принципах параллакса и стали основой для оценок размеров Солнечной системы почти на 2000 лет, пока прохождение Венеры в 1761 году не было правильно обнаружено . 1769. [29] Этот метод был предложен Эдмоном Галлеем в 1716 году, но он не дожил до результатов. Использование транзитов Венеры оказалось менее успешным, чем надеялись, из-за эффекта черной капли , но полученная оценка, 153 миллиона километров, всего на 2% выше принятого в настоящее время значения, 149,6 миллиона километров.
Намного позже Солнечную систему «масштабировали» с помощью параллакса астероидов , некоторые из которых, например Эрос , проходят гораздо ближе к Земле, чем Венера. В благоприятном противостоянии Эрос может приблизиться к Земле на расстояние 22 миллионов километров. [33] Во время противостояния 1900–1901 годов была запущена всемирная программа по измерению параллакса Эроса для определения солнечного параллакса (или расстояния до Солнца), результаты которого были опубликованы в 1910 году Артуром Хинксом из Кембриджа. [34] и Чарльз Д. Перрин из Ликской обсерватории университета Калифорнийского . [35]
Перрин опубликовал отчеты о ходе работы в 1906 году. [36] и 1908 год. [37] Он сделал 965 фотографий с помощью рефлектора Кроссли и выбрал 525 для измерения. [38] Аналогичная программа была затем реализована, при более близком подходе, в 1930–1931 годах Гарольдом Спенсером Джонсом . [39] Значение астрономической единицы (примерно расстояния Земля-Солнце), полученное с помощью этой программы, считалось определяющим до 1968 года, когда методы радиолокации и динамического параллакса начали давать более точные измерения.
Также радиолокационные отражения, как от Венеры (1958 г.), так и от астероидов, таких как Икар для определения солнечного параллакса использовались . Сегодня использование каналов космического корабля телеметрических решило эту старую проблему. В настоящее время принятое значение солнечного параллакса составляет 8,794143 угловых секунды. [40]
Параллакс движущегося кластера
[ редактировать ]Открытое звездное скопление Гиады в Тельце простирается на такую большую часть неба, на 20 градусов, что собственные движения, полученные на основе астрометрии, кажутся сходящимися с некоторой точностью к точке перспективы к северу от Ориона. Сочетание наблюдаемого видимого (углового) собственного движения в секундах дуги с также наблюдаемым истинным (абсолютным) удаляющимся движением, о чем свидетельствует доплеровское красное смещение звездных спектральных линий, позволяет оценить расстояние до скопления (151 световой год) и звезды его участников почти так же, как и при использовании годового параллакса. [41]
Динамический параллакс
[ редактировать ]Динамический параллакс иногда также использовался для определения расстояния до сверхновой, когда видно, что оптический волновой фронт вспышки распространяется через окружающие пылевые облака с кажущейся угловой скоростью, в то время как известно, что его истинная скорость распространения равна скорости света . [42]
Пространственно-временной параллакс
[ редактировать ]На основе усовершенствованных позиционирования релятивистских систем был разработан пространственно-временной параллакс, обобщающий обычное представление о параллаксе только в пространстве. Тогда поля событий в пространстве-времени можно вывести напрямую, без промежуточных моделей отклонения света массивными телами, таких как, например, используемая в формализме PPN . [43]
Статистический параллакс
[ редактировать ]Два связанных метода могут определять средние расстояния до звезд путем моделирования движения звезд. Оба называются статистическими параллаксами или по отдельности называются вековыми параллаксами и классическими статистическими параллаксами.
Движение Солнца в пространстве обеспечивает более длинную базовую линию, что повысит точность измерений параллакса, известного как вековой параллакс . Для звезд диска Млечного Пути это соответствует средней базовой величине 4 а.е. в год. Для звезд с гало базовый уровень составляет 40 а.е. в год. Через несколько десятилетий базовая линия может быть на порядки больше, чем базовая линия Земля-Солнце, используемая для традиционного параллакса. Вековый параллакс вводит более высокий уровень неопределенности, поскольку относительная скорость других звезд является дополнительным неизвестным. При применении к выборкам из нескольких звезд неопределенность можно уменьшить; точность обратно пропорциональна квадратному корню из размера выборки. [44]
Средние параллаксы и расстояния большой группы звезд можно оценить по их лучевым скоростям и собственным движениям . Это известно как классический статистический параллакс . Движения звезд моделируются таким образом, чтобы статистически воспроизводить дисперсию скоростей в зависимости от расстояния до них. [44] [45]
Другие методы измерения расстояний в астрономии
[ редактировать ]В астрономии термин «параллакс» стал означать метод оценки расстояний, не обязательно использующий истинный параллакс, например:
См. также
[ редактировать ]Примечания
[ редактировать ]- ^ Один триллион здесь — это короткая шкала , т.е. 10 12 (один миллион миллионов или миллиард в длинном масштабе).
Ссылки
[ редактировать ]- ^ Перриман, MAC; и др. (1999). «Каталог HIPPARCOS». Астрономия и астрофизика . 323 : L49–L52. Бибкод : 1997A&A...323L..49P .
- ^ Харрингтон, доктор юридических наук; Виллар, Р. (10 апреля 2014 г.). «Хаббл НАСА продлил звездную рулетку в 10 раз дальше в космос» . НАСА . Архивировано из оригинала 17 февраля 2019 года . Проверено 17 октября 2014 г.
- ^ Рисс, АГ; Казертано, С.; Андерсон, Дж.; МакКенти, Дж.; Филиппенко, А.В. (2014). «Параллакс за пределами килопарсека по результатам пространственного сканирования широкоугольной камерой 3 на космическом телескопе Хаббл». Астрофизический журнал . 785 (2): 161. arXiv : 1401.0484 . Бибкод : 2014ApJ...785..161R . дои : 10.1088/0004-637X/785/2/161 . S2CID 55928992 .
- ^ Браун, АГА ; и др. (сотрудничество Gaia) (август 2018 г.). « Выпуск данных Gaia 2: Краткое описание содержания и свойств опроса» . Астрономия и астрофизика . 616 . А1. arXiv : 1804.09365 . Бибкод : 2018A&A...616A...1G . дои : 10.1051/0004-6361/201833051 .
- ^ Б., Байдьянатх (2003). Введение в астрофизику . PHI Learning Private Limited. ISBN 978-81-203-1121-3 .
- ^ «Хаббл обнаружил, что Вселенная может расширяться быстрее, чем ожидалось» . Архивировано из оригинала 11 сентября 2018 года . Проверено 3 июня 2016 г.
- ^ «Хаббл растягивает звездную рулетку в десять раз дальше» . Изображения ЕКА/Хаббла . Архивировано из оригинала 30 октября 2017 года . Проверено 12 апреля 2014 г.
- ^ Поповски, П.; Гулд, А. (1998). «Математика статистического параллакса и локальной шкалы расстояний». arXiv : astro-ph/9703140 .
- ^ Бартель, Н.; и др. (1994). «Форма, скорость расширения и расстояние до сверхновой 1993J по данным РСДБ-измерений». Природа . 368 (6472): 610–613. Бибкод : 1994Natur.368..610B . дои : 10.1038/368610a0 . S2CID 4316734 .
- ^ «Весы космических расстояний – Млечный Путь» . Проверено 24 сентября 2014 г.
- ^ Бенедикт, Г.Ф.; и др. «Астрометрическая стабильность и точность датчика точного наведения № 3: параллакс и правильное движение Проксимы Центавра» (PDF) . Материалы семинара по калибровке HST . стр. 380–384 . Проверено 11 июля 2007 г.
- ^ «Далекие звезды» . Звездная дата . Техасский университет в Остине . 15 мая 2021 г. Проверено 5 сентября 2021 г.
- ^ Дайсон, Ф.В. (март 1913 г.). «Распределение в пространстве звезд в циркумполярном каталоге Кэррингтона» . Ежемесячные уведомления Королевского астрономического общества . 73 (5): 342. Бибкод : 1913MNRAS..73..334D . дои : 10.1093/mnras/73.5.334 .
[ абзац 14, стр. 342 ] Примем за единицу расстояния R* единицу, соответствующую параллаксу 1″·0 [… Сноска:]
* Для этой единицы расстояния необходимо дать название. Г-н Шарлье предложил «Сириометр» , но если игнорировать насилие над греческим языком, слово «Астрон» можно было бы принять . Профессор Тернер предлагает использовать парсек , который можно понимать как сокращенную форму «расстояния, соответствующего параллаксу в одну секунду». - ^ Кокс, Артур Н., изд. (2000). Астрофизические величины Аллена (4-е изд.). Нью-Йорк: AIP Press / Springer. Бибкод : 2000asqu.book.....C . ISBN 978-0387987460 .
- ^ Бинни, Джеймс; Тремейн, Скотт (2008). Галактическая динамика (2-е изд.). Принстон, Нью-Джерси: Издательство Принстонского университета. Бибкод : 2008gady.book.....B . ISBN 978-0-691-13026-2 .
- ^ Зейлик и Грегори 1998 , с. 44 .
- ^ Zeilik & Gregory 1998 , § 22-3, .
- ^ Бенедикт, Г. Фриц и др. (1999). «Интерферометрическая астрометрия Проксимы Центавра и звезды Барнарда с использованием датчика точного наведения 3 космического телескопа Хаббл: пределы обнаружения субзвездных спутников». Астрономический журнал . 118 (2): 1086–1100. arXiv : Astro-ph/9905318 . Бибкод : 1999AJ....118.1086B . дои : 10.1086/300975 . S2CID 18099356 .
- ↑ Перейти обратно: Перейти обратно: а б Харрингтон, доктор юридических наук; Виллард, Рэй (10 апреля 2014 г.). «Хаббл НАСА продлил звездную рулетку в 10 раз дальше в космос» . НАСА . Архивировано из оригинала 12 апреля 2014 года . Проверено 11 апреля 2014 г.
- ^ Добжицкий, Дж. (1973). Добжицкий, Ежи (ред.). Рецепция гелиоцентрической теории Коперника . стр. 51. doi : 10.1007/978-94-015-7614-7 . ISBN 978-90-481-8340-1 .
- ^ «Союз СТ-Б» успешно запустил космическую обсерваторию «Гея» . nasaspaceflight.com. 19 декабря 2013 года. Архивировано из оригинала 19 декабря 2013 года . Проверено 19 декабря 2013 г.
- ^ Хенни, Пол Дж. «Миссия Европейского космического агентства Гайя по изучению звезд» . Астрономия сегодня. Архивировано из оригинала 17 марта 2008 г. Проверено 8 марта 2008 г.
- ^ Зайдельманн, П. Кеннет (2005). Пояснительное приложение к Астрономическому альманаху . Университетские научные книги. стр. 123–125 . ISBN 978-1-891389-45-0 .
- ^ Барбьери, Чезаре (2007). Основы астрономии . ЦРК Пресс. стр. 132–135. ISBN 978-0-7503-0886-1 .
- ^ Ван Хелден, А. (2010). Измерение Вселенной: космические измерения от Аристарха до Галлея . Издательство Чикагского университета. Ч. 12.
- ↑ Перейти обратно: Перейти обратно: а б «Д». Астрономический альманах . [Министерство обороны] Военно-морское ведомство, Военно-морская обсерватория, Управление морского альманаха. 1981.
- ^ Астрономический альманах . [Министерство обороны] Военно-морское ведомство, Военно-морская обсерватория, Управление морского альманаха. 1981. с. М10.
- ^ Военно-морская обсерватория США. Офис морского альманаха; Великобритания. Морской альманах (2006). Пояснительное приложение к Астрономическому альманаху . Университетские научные книги. п. 125 . ISBN 978-1-891389-45-0 .
- ↑ Перейти обратно: Перейти обратно: а б с Гуцвиллер, Мартин К. (1998). «Луна-Земля-Солнце: старейшая задача трех тел». Обзоры современной физики . 70 (2): 589–639. Бибкод : 1998РвМП...70..589Г . дои : 10.1103/RevModPhys.70.589 .
- ^ Уэбб, Стивен (1999), «3.2 Аристарх, Гиппарх и Птолемей», Измерение Вселенной: лестница космологических расстояний , Springer, стр. 27–35, ISBN 9781852331061 . См., в частности, стр. 33: «Почти все, что мы знаем о Гиппархе, дошло до нас от Птолемея».
- ^ Фридман, WL (2000). «Постоянная Хаббла и возраст расширения Вселенной». Отчеты по физике . 333 (1): 13–31. arXiv : astro-ph/9909076 . Бибкод : 2000PhR...333...13F . дои : 10.1016/S0370-1573(00)00013-2 . S2CID 413222 .
- ^ Аль-Халили, Джим (2010), Следопыты: золотой век арабской науки , Penguin UK, стр. 270, ISBN 9780141965017 , заархивировано из оригинала 17 марта 2015 г.
Некоторые предполагают, что его расчет относительного размера Земли и Солнца привел Аристарха к выводу, что для Земли имело больше смысла вращаться вокруг гораздо большего Солнца, чем другое. в обход.
- ^ Уиппл 2007 , с. 47 .
- ^ Хинкс, Артур Р. (1909). «Документы о солнечном параллаксе № 7: общее решение на основе фотографических прямых восхождений Эроса в противостоянии 1900 года» . Ежемесячные уведомления Королевского астрономического общества . 69 (7): 544–67. Бибкод : 1909MNRAS..69..544H . дои : 10.1093/mnras/69.7.544 .
- ^ Перрин, Чарльз Д. (1910). Определение солнечного параллакса по фотографиям Эроса, сделанным с помощью рефлектора Кроссли Ликской обсерватории Калифорнийского университета (Первое изд.). Вашингтон, округ Колумбия: Вашингтонский Институт Карнеги. стр. 1–104.
- ^ Перрин, компакт-диск (1906). «Измерение и уменьшение фотографий Эроса, сделанных с помощью рефлектора Кроссли в 1900 году». Публикации Тихоокеанского астрономического общества . 18 (10): 226.
- ^ Перрин, Чарльз Д. (1908). «Прогресс в работе над солнечным параллаксом Эрос Кроссли» . Публикации Тихоокеанского астрономического общества . 20 (120): 184. Бибкод : 1908PASP...20..184P . дои : 10.1086/121816 . S2CID 121782316 .
- ^ Кэмпбелл, WW (1906). «Отчеты обсерваторий: Ликская обсерватория». Публикации Тихоокеанского астрономического общества . 19 (113): 92.
- ^ Джонс, Х. Спенсер (1941). «Солнечный параллакс и масса Луны по наблюдениям Эроса в противостоянии 1931 года». Память Рой. Астрон. Соц . 66 : 11–66.
- ^ «Астрономические константы» (PDF) . Военно-морская обсерватория США . Архивировано из оригинала (PDF) 20 июля 2011 г.
- ^ Виджай К. Нараянан; Эндрю Гулд (1999). «Точный тест систематики Hipparcos в отношении Гиад». Астрофизический журнал . 515 (1): 256. arXiv : astro-ph/9808284 . Бибкод : 1999ApJ...515..256N . дои : 10.1086/307021 . S2CID 15351552 .
- ^ Панагия, Н.; Гилмоцци, Р.; Макчетто, Ф.; Адорф, Х.-М.; и др. (1991). «Свойства околозвездного кольца SN 1987A и расстояние до Большого Магелланова Облака». Астрофизический журнал . 380 : Л23. Бибкод : 1991ApJ...380L..23P . дои : 10.1086/186164 .
- ^ Рубин, Дж.Л. (2015). «Релятивистские пентаметрические координаты из релятивистских локализующих систем и проективная геометрия пространственно-временного многообразия» . Электронный журнал теоретической физики . 12 (32): 83–112. Архивировано из оригинала 8 февраля 2015 г.
- ↑ Перейти обратно: Перейти обратно: а б Поповски, Петр; Гулд, Эндрю (29 января 1998 г.). «Математика статистического параллакса и локальной шкалы расстояний» . arXiv : astro-ph/9703140 . Бибкод : 1997astro.ph..3140P .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) - ^ Лейден, Эндрю С; Хэнсон, Роберт Б; Хоули, Сюзанна Л; Клемола, Арнольд Р.; Хэнли, Кристофер Дж (1996). «Абсолютная величина и кинематика звезд RR Лиры через статистический параллакс». Астрономический журнал . 112 : 2110. arXiv : astro-ph/9608108 . Бибкод : 1996AJ....112.2110L . дои : 10.1086/118167 . S2CID 8732647 .
