Квадратные одногранные соты порядка 4
| Квадратные одногранные соты порядка 4 | |
|---|---|
 Централизованно проецируется на сферу | |
| Тип | Вырожденные обычные соты |
| Символ Шлефли | {2,4,4} |
| Диаграммы Кокстера | |
| Клетки | {2,4} |
| Лица | {2} |
| Краевая фигура | {4} |
| Вершинная фигура | {4,4}  |
| Двойной | Заказать-2 квадратная плитка сотовая |
| Группа Коксетера | [2,4,4] |
| Характеристики | Обычный |
В геометрии представляют квадратные одногранные соты 4-го порядка , заполняющую пространство собой правильную мозаику (или соты ) с символом Шлефли {2,4,4}. По каждому краю у него 4 квадратных осоэдра {2,4}. Другими словами, это упаковка бесконечно высоких квадратных колонн. Это вырожденные соты в евклидовом пространстве, но их можно рассматривать как проекцию на сферу. Его вершинная фигура, квадратная мозаика , видна на каждом полушарии.
Изображения
[ редактировать ]Стереографические проекции сферической проекции, все края которых проецируются в круги.
 Центрировано на полюсе |
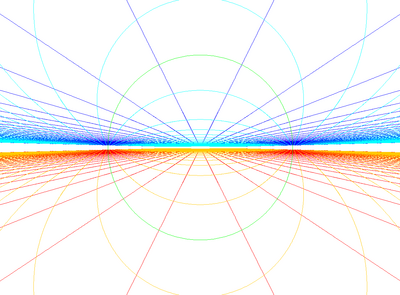 С центром на экваторе |
Связанные соты
[ редактировать ]Это часть последовательности сот с квадратной фигурой вершин:
| {p,4,4} соты |
|---|
Усеченные квадратные одногранные соты порядка 4
[ редактировать ]| Заказать-2 квадратная плитка сотовая Усеченные квадратные одногранные соты порядка 4  Частичная мозаика с кубами поочередного цвета. | |
|---|---|
| Тип | однородные выпуклые соты |
| Символ Шлефли | {4,4}×{} |
| Диаграммы Кокстера | |
| Клетки | {3,4} |
| Лица | {4} |
| Вершинная фигура | Квадратная пирамида |
| Двойной | |
| Группа Коксетера | [2,4,4] |
| Характеристики | Униформа |
Соты {2,4,4} можно усечь до t{2,4,4} или {}×{4,4}, диаграмма Кокстера. ![]()
![]()
![]()
![]()
![]()
![]()
![]() , представленный как слой кубов, частично показанный здесь с кубическими ячейками попеременного цвета. Торольд Госсет идентифицировал эти полуправильные бесконечные соты как кубическую полуклетку .
, представленный как слой кубов, частично показанный здесь с кубическими ячейками попеременного цвета. Торольд Госсет идентифицировал эти полуправильные бесконечные соты как кубическую полуклетку .
Чередование этих сот, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , состоит из бесконечных квадратных пирамид и бесконечных тетраэдров , между двумя квадратными мозаиками .
, состоит из бесконечных квадратных пирамид и бесконечных тетраэдров , между двумя квадратными мозаиками .
См. также
[ редактировать ]- Треугольные одногранные соты порядка 6
- Тетраэдрические соты порядка 7
- Список правильных многогранников
Ссылки
[ редактировать ]- Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Глава 10, Обычные соты в гиперболическом пространстве )











