Индекс Жаккара

Пересечение и объединение двух множеств A и B

Пересечение над объединением как мера сходства для обнаружения объектов на изображениях – важная задача компьютерного зрения .

Индекс Жаккара , также известный как коэффициент сходства Жаккара , представляет собой статистику, используемую для оценки сходства и разнообразия наборов выборок .

Он был разработан Гроувом Карлом Гилбертом в 1884 году как коэффициент проверки (v). и теперь его часто называют критическим индексом успеха в метеорологии. Позже он был независимо разработан Полем Жаккаром , первоначально дав французское название коэффициент де communauté , и независимо сформулированный снова Т. Танимото. его также называют индексом Танимото или коэффициентом Танимото Таким образом, в некоторых областях . Однако они идентичны в том, что обычно принимают отношение размера пересечения к объединению .

Обзор

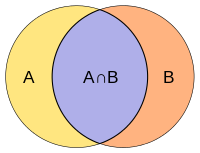
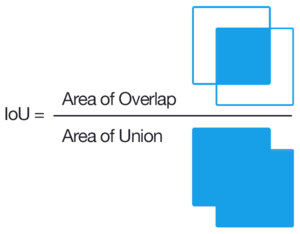
Коэффициент Жаккара измеряет сходство между конечными наборами выборок и определяется как размер пересечения, деленный на размер объединения наборов выборок:

$J(A,B)={\frac {|A\cap B|}{|A\cup B|}}={\frac {|A\cap B|}{|A|+|B|-|A\cap B|}}.$

Обратите внимание, что по замыслу $0\leq J(A,B)\leq 1.$ Если A пересечение B пусто, то J ( A , B ) = 0. Коэффициент Жаккара широко используется в информатике, экологии, геномике и других науках, где двоичные или бинаризованные данные используются . Для проверки гипотез с помощью коэффициента Жаккара доступны как методы точного решения, так и методы аппроксимации.

Сходство Жаккара применимо и к сумкам, т. е. мультисетам . Здесь есть аналогичная формула, но используемые символы обозначают пересечение сумок и сумму сумок (а не объединение). Максимальное значение — 1/2.

$J(A,B)={\frac {|A\cap B|}{|A\uplus B|}}={\frac {|A\cap B|}{|A|+|B|}}.$

Расстояние Жаккара , которое измеряет несходство между наборами выборок, является дополнительным к коэффициенту Жаккара и получается путем вычитания коэффициента Жаккара из 1 или, что то же самое, путем деления разницы размеров объединения и пересечения двух наборов на размер союза:

$d_{J}(A,B)=1-J(A,B)={\frac {|A\cup B|-|A\cap B|}{|A\cup B|}}.$

Альтернативная интерпретация расстояния Жаккара - как отношение размера симметричной разности $A\mathbin {\triangle } B=(A\cup B)-(A\cap B)$ в профсоюз. Расстояние Жаккара обычно используется для расчета n × n для кластеризации и многомерного масштабирования n матрицы размера наборов выборок.

Это расстояние является метрикой совокупности всех конечных множеств.

Существует также версия расстояния Жаккара для мер , включая вероятностные меры . Если $\mu$ является мерой измеримого пространства $X$, то мы определяем коэффициент Жаккара как

$J_{\mu }(A,B)={\frac {\mu (A\cap B)}{\mu (A\cup B)}},$

и расстояние Жаккара на

$d_{\mu }(A,B)=1-J_{\mu }(A,B)={\frac {\mu (A\mathbin {\triangle } B)}{\mu (A\cup B)}}.$

Необходимо соблюдать осторожность, если $\mu (A\cup B)=0$ или $\infty$, поскольку в этих случаях эти формулы не определены четко.

Схема MinHash с независимыми и независимыми перестановками, хеширования чувствительной к локальности , может использоваться для эффективного вычисления точной оценки коэффициента сходства Жаккара пар наборов, где каждый набор представлен сигнатурой постоянного размера, полученной из минимальных значений хеш-функции. .

Сходство асимметричных двоичных атрибутов

Учитывая два объекта, A и B , каждый из которых имеет n двоичных атрибутов, коэффициент Жаккара является полезной мерой перекрытия, которое A и B разделяют со своими атрибутами. Каждый атрибут A и B может иметь значение 0 или 1. Общее количество каждой комбинации атрибутов для A и B определяется следующим образом:

$M_{11}$ представляет общее количество атрибутов, где A и B имеют значение 1.

$M_{01}$ представляет общее количество атрибутов, где атрибут A равен 0, а атрибут B равен 1.

$M_{10}$ представляет общее количество атрибутов, где атрибут A равен 1, а атрибут B равен 0.

$M_{00}$ представляет общее количество атрибутов, где A и B имеют значение 0.

А Б	0	1
0	$M_{00}$	$M_{10}$
1	$M_{01}$	$M_{11}$

Каждый атрибут должен относиться к одной из этих четырех категорий, а это означает, что

$M_{11}+M_{01}+M_{10}+M_{00}=n.$

Коэффициент подобия Жаккара J определяется как

$J={M_{11} \over M_{01}+M_{10}+M_{11}}.$

Расстояние Жаккара d _J определяется как

$d_{J}={M_{01}+M_{10} \over M_{01}+M_{10}+M_{11}}=1-J.$

Статистические выводы можно сделать на основе коэффициентов сходства Жаккара и, следовательно, связанных с ними показателей. Учитывая два набора выборок A и B с n атрибутами, можно провести статистическую проверку, чтобы увидеть, является ли перекрытие статистически значимым . Точное решение доступно, хотя вычисления могут быть дорогостоящими по мере увеличения n . Доступны методы оценки либо путем аппроксимации полиномиального распределения , либо путем начальной загрузки.

Отличие от простого коэффициента соответствия (SMC)

При использовании для двоичных атрибутов индекс Жаккара очень похож на простой коэффициент соответствия . Основное отличие состоит в том, что в SMC есть термин $M_{00}$ в числителе и знаменателе, тогда как индекс Жаккара этого не делает. Таким образом, SMC считает как взаимное присутствие (когда атрибут присутствует в обоих наборах), так и взаимное отсутствие (когда атрибут отсутствует в обоих наборах) как совпадения и сравнивает их с общим количеством атрибутов во вселенной, тогда как индекс Жаккара только считает взаимное присутствие совпадением и сравнивает его с количеством атрибутов, выбранных хотя бы одним из двух наборов.

Например, при анализе рыночной корзины корзина двух потребителей, которых мы хотим сравнить, может содержать лишь небольшую часть всех доступных продуктов в магазине, поэтому SMC обычно возвращает очень высокие значения сходства, даже если корзины имеют очень большое сходство. малое сходство, что делает индекс Жаккара более подходящим показателем сходства в этом контексте. Например, рассмотрим супермаркет с 1000 товарами и двумя покупателями. В корзине первого покупателя соль и перец, а в корзине второго — соль и сахар. В этом сценарии сходство между двумя корзинами, измеренное индексом Жаккара, составит 1/3, но при использовании SMC сходство становится 0,998.

В других контекстах, где 0 и 1 несут эквивалентную информацию (симметрию), SMC является лучшей мерой сходства. Например, векторы демографических переменных, хранящихся в фиктивных переменных , таких как пол, лучше сравнивать с SMC, чем с индексом Жаккара, поскольку влияние пола на сходство должно быть одинаковым, независимо от того, определяется ли мужской пол как 0, а женский. как 1 или наоборот. Однако, когда у нас есть симметричные фиктивные переменные, можно воспроизвести поведение SMC, разделив фиктивные переменные на два двоичных атрибута (в данном случае, мужской и женский), преобразуя их таким образом в асимметричные атрибуты, позволяя использовать индекс Жаккара без внесение какой-либо предвзятости. Однако SMC остается более эффективным в вычислительном отношении в случае симметричных фиктивных переменных, поскольку не требует добавления дополнительных измерений.

Взвешенное сходство и расстояние Жаккара

Если $\mathbf {x} =(x_{1},x_{2},\ldots ,x_{n})$ и $\mathbf {y} =(y_{1},y_{2},\ldots ,y_{n})$ два вектора со всеми действительными $x_{i},y_{i}\geq 0$, то их коэффициент сходства Жаккара (также известный как сходство Ружички) определяется как

$J_{\mathcal {W}}(\mathbf {x} ,\mathbf {y} )={\frac {\sum _{i}\min(x_{i},y_{i})}{\sum _{i}\max(x_{i},y_{i})}},$

и расстояние Жаккара (также известное тогда как расстояние Зёргеля)

$d_{J{\mathcal {W}}}(\mathbf {x} ,\mathbf {y} )=1-J_{\mathcal {W}}(\mathbf {x} ,\mathbf {y} ).$

В еще большей общности, если $f$ и $g$ две неотрицательные измеримые функции в измеримом пространстве $X$ с мерой $\mu$, то мы можем определить

$J_{\mathcal {W}}(f,g)={\frac {\int \min(f,g)d\mu }{\int \max(f,g)d\mu }},$

где $\max$ и $\min$ являются точечными операторами. Тогда расстояние Жаккара равно

$d_{J{\mathcal {W}}}(f,g)=1-J_{\mathcal {W}}(f,g).$

Тогда, например, для двух измеримых множеств $A,B\subseteq X$, у нас есть $J_{\mu }(A,B)=J(\chi _{A},\chi _{B}),$ где $\chi _{A}$ и $\chi _{B}$ являются характеристическими функциями соответствующего множества.

Вероятность Жаккара, сходство и расстояние

Описанное выше взвешенное подобие Жаккара обобщает индекс Жаккара на положительные векторы, где набор соответствует двоичному вектору, заданному индикаторной функцией , т.е. $x_{i}\in \{0,1\}$. Однако он не обобщает индекс Жаккара на распределения вероятностей, где набор соответствует равномерному распределению вероятностей, т.е.

$x_{i}={\begin{cases}{\frac {1}{|X|}}&i\in X\\0&{\text{otherwise}}\end{cases}}$

Всегда меньше, если наборы различаются по размеру. Если $|X|>|Y|$, и $x_{i}=\mathbf {1} _{X}(i)/|X|,y_{i}=\mathbf {1} _{Y}(i)/|Y|$ затем

$J_{\mathcal {W}}(x,y)={\frac {|X\cap Y|}{|X\setminus Y|+|X|}}<J(X,Y).$

Вероятностный индекс Жаккара можно интерпретировать как пересечение симплексов.

Вместо этого обобщение, которое является непрерывным между распределениями вероятностей и соответствующими наборами поддержки, имеет вид

$J_{\mathcal {P}}(x,y)=\sum _{x_{i}\neq 0,y_{i}\neq 0}{\frac {1}{\sum _{j}\max \left({\frac {x_{j}}{x_{i}}},{\frac {y_{j}}{y_{i}}}\right)}}$

которая называется «Вероятностью» Жаккара. Он имеет следующие ограничения на взвешенный Жаккар на векторах вероятности.

$J_{\mathcal {W}}(x,y)\leq J_{\mathcal {P}}(x,y)\leq {\frac {2J_{\mathcal {W}}(x,y)}{1+J_{\mathcal {W}}(x,y)}}$

Здесь верхней границей является (взвешенный) коэффициент Сёренсена–Дайса . Соответствующее расстояние, $1-J_{\mathcal {P}}(x,y)$, является метрикой распределений вероятностей и псевдометрикой неотрицательных векторов.

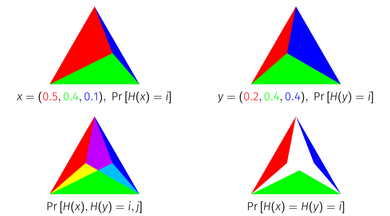
Вероятностный индекс Жаккара имеет геометрическую интерпретацию как площадь пересечения симплексов . Каждая точка на единице $k$-симплекс соответствует распределению вероятностей на $k+1$ элементы, поскольку единица $k$-симплекс – это множество точек в $k+1$ размеры, сумма которых равна 1. Чтобы геометрически получить индекс Жаккара вероятности, представьте распределение вероятностей в виде единичного симплекса, разделенного на подсимплексы в соответствии с массой каждого предмета. Если вы наложите два распределения, представленных таким образом, друг на друга и пересечете симплексы, соответствующие каждому элементу, оставшаяся площадь будет равна индексу Жаккара вероятности распределений.

Оптимальность вероятностного индекса Жаккара

Наглядное доказательство оптимальности индекса Жаккара вероятности для трехэлементных распределений.

Рассмотрим задачу построения случайных величин так, чтобы они как можно чаще сталкивались друг с другом. То есть, если $X\sim x$ и $Y\sim y$, мы хотели бы построить $X$ и $Y$ максимизировать $\Pr[X=Y]$. Если мы посмотрим только на два распределения $x,y$ изолированно, высший $\Pr[X=Y]$ мы можем достичь, определяется выражением $1-{\text{TV}}(x,y)$ где ${\text{TV}}$ это расстояние общего изменения . Однако предположим, что нас интересует не только максимизация этой конкретной пары, предположим, что мы хотели бы максимизировать вероятность столкновения любой произвольной пары. Можно построить бесконечное количество случайных величин, по одной для каждого распределения. $x$и стремиться максимизировать $\Pr[X=Y]$ для всех пар $x,y$. В довольно строгом смысле, описанном ниже, индекс Жаккара вероятности является оптимальным способом выравнивания этих случайных величин.

Для любого метода отбора проб $G$ и дискретные распределения $x,y$, если $\Pr[G(x)=G(y)]>J_{\mathcal {P}}(x,y)$ тогда для некоторых $z$ где $J_{\mathcal {P}}(x,z)>J_{\mathcal {P}}(x,y)$ и $J_{\mathcal {P}}(y,z)>J_{\mathcal {P}}(x,y)$, или $\Pr[G(x)=G(z)]<J_{\mathcal {P}}(x,z)$ или $\Pr[G(y)=G(z)]<J_{\mathcal {P}}(y,z)$.

То есть ни один метод выборки не может достичь большего количества коллизий, чем $J_{\mathcal {P}}$ на одной паре, не добившись меньшего количества коллизий, чем $J_{\mathcal {P}}$ на другой паре, где приведенная пара более похожа при $J_{\mathcal {P}}$ чем увеличенная пара. Эта теорема верна для индекса Жаккара множеств (если интерпретировать его как равномерное распределение) и вероятности Жаккара, но не для взвешенного Жаккара. (В теореме используется слово «метод выборки» для описания совместного распределения по всем распределениям в пространстве, поскольку оно основано на использовании алгоритмов взвешенного минхеширования , которые достигают этого как вероятности столкновения.)

Эта теорема имеет наглядное доказательство для трехэлементных распределений с использованием симплексного представления.

Сходство и расстояние Танимото

В литературе и Интернете встречаются различные формы функций, описываемых как сходство Танимото и расстояние Танимото. Большинство из них являются синонимами сходства Жаккара и расстояния Жаккара, но некоторые математически различны. Множество источников цитировать технический отчет IBM как основополагающая ссылка. Отчет доступен в нескольких библиотеках .

В «Компьютерной программе для классификации растений», опубликованной в октябре 1960 г., Приведен метод классификации, основанный на коэффициенте сходства и производной функции расстояния. Кажется, это наиболее авторитетный источник по значению терминов «Сходство Танимото» и «Расстояние Танимото». Коэффициент сходства эквивалентен сходству Жаккара, но функция расстояния не совпадает с расстоянием Жаккара.

Определения сходства и расстояния Танимото

В этой статье «коэффициент сходства» дается для растровых изображений , где каждый бит массива фиксированного размера представляет наличие или отсутствие характеристики моделируемого объекта. Определение отношения — это количество общих битов, деленное на количество битов, установленных ( т.е. ненулевых) в любой выборке.

Представлено математически, если образцы X и Y являются растровыми изображениями, $X_{i}$ это i -й бит X , и $\land ,\lor$ являются побитовыми операторами и , или соответственно, то коэффициент подобия $T_{s}$ является

$T_{s}(X,Y)={\frac {\sum _{i}(X_{i}\land Y_{i})}{\sum _{i}(X_{i}\lor Y_{i})}}$

Если вместо этого каждая выборка моделируется как набор атрибутов, это значение равно коэффициенту Жаккара двух наборов. Жаккар в статье не цитируется, и вполне вероятно, что авторы об этом не знали.

Танимото далее определяет «коэффициент расстояния» на основе этого соотношения, определенного для растровых изображений с ненулевым сходством:

$T_{d}(X,Y)=-\log _{2}(T_{s}(X,Y))$

Этот коэффициент намеренно не является показателем расстояния. Он выбран таким образом, чтобы два образца, сильно отличающиеся друг от друга, были похожи на третий. Легко построить пример, опровергающий свойство неравенства треугольника .

Другие определения расстояния Танимото

Расстояние Танимото часто ошибочно называют синонимом расстояния Жаккара. $1-T_{s}$. Эта функция является правильной метрикой расстояния. «Расстояние Танимото» часто называют подходящим показателем расстояния, вероятно, из-за его путаницы с расстоянием Жаккара.

Если сходство Жаккара или Танимото выражается через битовый вектор, то его можно записать как

$f(A,B)={\frac {A\cdot B}{\|A\|^{2}+\|B\|^{2}-A\cdot B}}$

где тот же расчет выражается через векторное скалярное произведение и величину. Это представление основано на том факте, что для битового вектора (где значение каждого измерения равно 0 или 1) тогда

$A\cdot B=\sum _{i}A_{i}B_{i}=\sum _{i}(A_{i}\land B_{i})$

и

$\|A\|^{2}=\sum _{i}A_{i}^{2}=\sum _{i}A_{i}.$

Это потенциально запутанное представление, поскольку функция, выраженная над векторами, является более общей, если ее область определения явно не ограничена. Свойства $T_{s}$ не обязательно распространяются на $f$. В частности, разностная функция $1-f$ не сохраняет неравенство треугольника и, следовательно, не является правильной метрикой расстояния, тогда как $1-T_{s}$ является.

Существует реальная опасность того, что сочетание «Расстояния Танимото», определяемого с помощью этой формулы, с утверждением «Расстояние Танимото является правильной метрикой расстояния» приведет к ложному выводу о том, что функция $1-f$ на самом деле это метрика расстояния для векторов или мультимножеств в целом, тогда как ее использование в алгоритмах поиска по сходству или кластеризации может не дать правильных результатов.

Губы использует определение сходства Танимото, которое эквивалентно $f$, и относится к расстоянию Танимото как к функции $1-f$. Однако в статье ясно указано, что контекст ограничен использованием (положительного) весового вектора. $W$ такой, что для любого вектора A рассматриваемого $A_{i}\in \{0,W_{i}\}.$ В этих обстоятельствах функция является правильной метрикой расстояния, и поэтому набор векторов, управляемых таким весовым вектором, образует метрическое пространство под этой функцией.

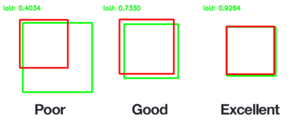
Индекс Жаккара в матрицах путаницы двоичной классификации

В матрицах путаницы, используемых для двоичной классификации , индекс Жаккара можно представить в виде следующей формулы:

${\text{Jaccard index}}={\frac {TP}{TP+FP+FN}}$

где TP — истинные положительные результаты, FP — ложные положительные результаты и FN — ложные отрицательные результаты.

См. также

• Коэффициент перекрытия
• Простой коэффициент соответствия
• Расстояние Хэмминга
• Коэффициент Сёренсена–Дайса , что эквивалентно: $J=S/(2-S)$ и $S=2J/(1+J)$ ( $J$: индекс Жаккара, $S$: коэффициент Сёренсена – Дайса)
• Индекс Тверского
• Корреляция
• Взаимная информация , нормализованным метрическим вариантом которой является энтропийное расстояние Жаккара.

Дальнейшее чтение

• Тан П.Н., Штайнбах М., Кумар В. (2005). Введение в интеллектуальный анализ данных . ISBN  0-321-32136-7 .

Внешние ссылки

• Конспекты лекций «Введение в интеллектуальный анализ данных» от Тана, Штайнбаха, Кумара
• Обнаружение особенностей спутниковых изображений Kaggle Dstl — оценка