Правило Судного дня

Джон Конвей , изобретатель алгоритма Судного дня

Правило Судного дня , Алгоритм Судного дня или Метод Судного дня — это алгоритм определения дня недели по заданной дате. Он обеспечивает вечный календарь , поскольку григорианский календарь движется циклами по 400 лет. Алгоритм мысленных вычислений был разработан Джоном Конвеем в 1973 году. черпая вдохновение из Льюиса Кэрролла алгоритма вечного календаря . Он использует преимущества того, что каждый год имеет определенный день недели, на который определенные легко запоминающиеся даты, называемые «судными днями выпадают »; например, последний день февраля, 4/4, 6/6, 8/8, 10/10 и 12/12 приходится на один и тот же день недели в любом году.

Применение алгоритма Судного дня включает в себя три этапа: определение опорного дня для столетия, вычисление опорного дня для года на основе даты для столетия и выбор ближайшей даты из тех, которые всегда выпадают на Судный день, например: 4/4 и 6/6, а также подсчет количества дней ( по модулю 7 ) между этой датой и рассматриваемой датой, чтобы получить день недели. Этот метод применим как к григорианскому календарю , так и к юлианскому календарю , хотя их судными днями обычно являются разные дни недели.

Алгоритм настолько прост, что его можно вычислить в уме. Конвей обычно мог дать правильный ответ менее чем за две секунды. Чтобы улучшить свою скорость, он практиковался в календарных вычислениях на своем компьютере, который был запрограммирован задавать ему случайные даты каждый раз, когда он входил в систему.

Якорные дни некоторых современных лет

Якорным днем ​​Судного дня в текущем году по григорианскому календарю (2024 г.) является четверг. По некоторым другим современным годам:

Якорные дни за годы с 1796 по 2105 год.

Воскресенье	Понедельник	Вторник	Среда	Четверг	Пятница	Суббота
	1796	1797	1798	1799	1800	1801
1802	1803		1804	1805	1806	1807
	1808	1809	1810	1811		1812
1813	1814	1815		1816	1817	1818
1819		1820	1821	1822	1823
1824	1825	1826	1827		1828	1829
1830	1831		1832	1833	1834	1835
	1836	1837	1838	1839		1840
1841	1842	1843		1844	1845	1846
1847		1848	1849	1850	1851
1852	1853	1854	1855		1856	1857
1858	1859		1860	1861	1862	1863
	1864	1865	1866	1867		1868
1869	1870	1871		1872	1873	1874
1875		1876	1877	1878	1879
1880	1881	1882	1883		1884	1885
1886	1887		1888	1889	1890	1891
	1892	1893	1894	1895		1896
1897	1898	1899	1900	1901	1902	1903
	1904	1905	1906	1907		1908
1909	1910	1911		1912	1913	1914
1915		1916	1917	1918	1919
1920	1921	1922	1923		1924	1925
1926	1927		1928	1929	1930	1931
	1932	1933	1934	1935		1936
1937	1938	1939		1940	1941	1942
1943		1944	1945	1946	1947
1948	1949	1950	1951		1952	1953
1954	1955		1956	1957	1958	1959
	1960	1961	1962	1963		1964
1965	1966	1967		1968	1969	1970
1971		1972	1973	1974	1975
1976	1977	1978	1979		1980	1981
1982	1983		1984	1985	1986	1987
	1988	1989	1990	1991		1992
1993	1994	1995		1996	1997	1998
1999		2000	2001	2002	2003
2004	2005	2006	2007		2008	2009
2010	2011		2012	2013	2014	2015
	2016	2017	2018	2019		2020
2021	2022	2023		2024	2025	2026
2027		2028	2029	2030	2031
2032	2033	2034	2035		2036	2037
2038	2039		2040	2041	2042	2043
	2044	2045	2046	2047		2048
2049	2050	2051		2052	2053	2054
2055		2056	2057	2058	2059
2060	2061	2062	2063		2064	2065
2066	2067		2068	2069	2070	2071
	2072	2073	2074	2075		2076
2077	2078	2079		2080	2081	2082
2083		2084	2085	2086	2087
2088	2089	2090	2091		2092	2093
2094	2095		2096	2097	2098	2099
2100	2101	2102	2103		2104	2105

Таблица заполняется горизонтально, пропуская по одному столбцу для каждого високосного года. Эта таблица повторяется каждые 28 лет, за исключением годов григорианского календаря, кратных 100 (например, 1800, 1900 и 2100, которые не являются високосными годами), которые также не кратны 400 (например, 2000, который все еще является високосный год). Полный цикл составляет 28 лет (1461 неделя) по юлианскому календарю и 400 лет (20871 неделя) по григорианскому календарю.

Памятные даты, которые всегда приходятся на Судный день

Можно найти день недели данной календарной даты, используя ближайший конец света в качестве ориентира. Чтобы помочь в этом, ниже приводится список легко запоминающихся дат каждого месяца, которые всегда приходятся на конец света.

Последний день февраля всегда является судным днем. Для января 3 января является судным днем ​​в невисокосные годы, а 4 января - судным днем ​​в високосные годы, которые можно запомнить как «3-е в течение 3 лет из 4 и 4-е в 4-м году». Для марта можно запомнить либо День Пи , либо « 0 марта », причем последнее относится к дню перед 1 марта, то есть к последнему дню февраля.

С апреля по декабрь четные месяцы обозначаются двойными датами: 4/4, 6/6, 8/8, 10/10 и 12/12, причем все они приходятся на Судный день. Нечетные месяцы можно запомнить мнемоникой «Работаю с 9 до 5 в 7-11 », т. е. 5/9, 11/7, а также 9/5 и 11/7 – это все дни конца света (это верно как для соглашений «День/Месяц», так и для «Месяц/День»).

Несколько известных дат, таких как День независимости в США , День подарков и День святого Валентина в невисокосные годы, также каждый год выпадают на конец света. В приведенной ниже таблице представлены только мнемоники, представленные в перечисленных источниках.

Месяц	Памятная дата	Месяц/День	Мнемоника	Полный список дней
январь	3 января (независимые годы), 4 января (високосные годы)	1/3 ИЛИ 1/4 (1/31 ИЛИ 1/32)	3-й 3 года в 4 и 4-й в 4 -м (или: последний день января, притворяясь, что в високосные годы приходится 32 января. )	3 , 10, 17, 24, 31 ИЛИ 4 , 11, 18, 25, 32
февраль	28 февраля (невисокосные годы), 29 февраля (високосные годы)	2/0 ИЛИ 2/1 (2/28 ИЛИ 2/29)	последний день января, притворяясь, что в високосные годы приходится 32 января. (или: последний день февраля)	0, 7, 14, 21, 28 ИЛИ 1, 8, 15, 22, 29
Маршировать	« 0 марта », 14 марта.	3/0 И 3/14	последний день февраля, День Пи	0 , 7, 14 , 21, 28
апрель	4 апреля	4/4	4/4 , 6/6, 8/8, 10/10, 12/12	4 , 11, 18, 25
Может	9 мая	5/9	с 9 до 5 в 7-11	2, 9 , 16, 23, 30
Июнь	6 июня	6/6	4/4, 6/6 , 8/8, 10/10, 12/12	6 , 13, 20, 27
Июль	11 июля	7/11	с 9 до 5 в 7-11	4, 11 , 18, 25
Август	8 августа	8/8	4/4, 6/6, 8/8 , 10/10, 12/12	1, 8 , 15, 22, 29
Сентябрь	5 сентября	9/5	с 9 до 5 в 7-11	5 , 12, 19, 26
Октябрь	10 октября	10/10	4/4, 6/6, 8/8, 10/10 , 12/12	3, 10 , 17, 24, 31
ноябрь	7 ноября	11/7	с 9 до 5 в 7-11	7 , 14, 21, 28
декабрь	12 декабря	12/12	4/4, 6/6, 8/8, 10/10, 12/12	5, 12 , 19, 26

Поскольку конец света для конкретного года напрямую связан с будними днями дат в период с марта по февраль следующего года, то для января и февраля того же года приходится выделять невисокосные и високосные годы.

Месяц	М	Конец света
Ян	1	3/4	К/Л	К/Д
февраль	2	0/1
Мар	3	7/0	М + 4	день С
Может	5	9
июль	7	11
Сентябрь	9	5	М − 4
ноябрь	11	7
Ян	13	9/2		День Б
апрель	4	4	М	день С
июнь	6	6
август	8	8
октябрь	10	10
декабрь	12	12
февраль	14	13/−1	М - 1	День Б

Январь и февраль можно считать последними двумя месяцами предыдущего года.

Пример

Чтобы узнать, в какой день недели Рождество 2021 года, действуйте следующим образом: в 2021 году Судный день приходится на воскресенье. Поскольку 12 декабря — Судный день, 25 декабря, будучи спустя тринадцать дней (на две недели меньше дня), выпало на субботу. Рождество всегда является днем ​​недели перед судным днем. Кроме того, 4 июля ( День независимости США ) всегда приходится на тот же день недели, что и Судный день, как и Хэллоуин (31 октября), День Пи (14 марта) и 26 декабря ( День подарков ).

Мнемонические названия дней недели

Поскольку этот алгоритм предполагает обработку дней недели как чисел по модулю 7, Джон Конвей предложил думать о днях недели как «Нет дня» или «Суббота» (воскресенье), «Один день», «Два дня», «Тройной день», Четверодневка», «Пятидневка» и «Шестидневка», чтобы вспомнить соотношение числа и дня недели, не пересчитывая их в голове.

день недели	Индекс число	Мнемоника
Воскресенье	0	Ни дня или Сандей
Понедельник	1	Один день
Вторник	2	Двухдневный
Среда	3	Треблсдей
Четверг	4	Четверной день
Пятница	5	Пятидневный
Суббота	6	Шесть в день

Есть некоторые языки, такие как славянские языки , китайский , греческий , португальский , галисийский и иврит , в которых названия дней недели основаны на их позиционном порядке . Славяне и китайцы согласны с приведенной выше таблицей; другие упомянутые языки считаются с воскресенья первым днем.

В поисках якорного дня года

Сначала возьмем якорный день за столетие. Для целей правила Судного дня столетие начинается с 00-го года и заканчивается 99-м. В следующей таблице показаны опорные дни столетий 1600–1699, 1700–1799, 1800–1899, 1900–1999, 2000–2099, 2100–2199 и 2200–2299.

Века	Якорный день	Мнемоника	Индекс (день недели)
1600–1699	Вторник	—	2 (Два дня)
1700–1799	Воскресенье	—	0 (недневной)
1800–1899	Пятница	—	5 (Пятидневка)
1900–1999	Среда	Мы в прошлом дне (большинство ныне живущих людей родились в том веке)	3 (Тройной день)
2000–2099	Вторник	Г-Вторник-К или Два дня ( Y2K был во главе этого столетия)	2 (вторник)
2100–2199	Воскресенье	Двадцать один день — воскресенье (2100 год – начало следующего столетия)	0 (недневной)
2200–2299	Пятница	—	5 (Пятидневка)

Для григорианского календаря:

Математическая формула

5 × ( c mod 4) mod 7 + вторник = якорь.

алгоритмический

Пусть r = c mod 4

если r = 0, то якорь = вторник

если r = 1 , то якорь = воскресенье

если r = 2 , то якорь = пятница

если r = 3 , то якорь = среда

Для юлианского календаря:

6 c mod 7 + воскресенье = якорь.

Примечание: $c={\biggl \lfloor }{{\text{year}} \over 100}{\biggr \rfloor }$.

Затем найдите опорный день года. Чтобы добиться этого, по словам Конвея:

1. Разделите две последние цифры года (назовем это y ) на 12 и пусть a будет нижней частью частного .
2. Пусть b — остаток того же частного.
3. Разделите остаток на 4 и пусть c будет нижней частью частного.
4. Пусть d будет суммой трех чисел ( d = a + b + c ). (Здесь снова можно разделить на семь и взять остаток. Это число, как и должно быть, эквивалентно y плюс нижний предел y, разделенный на четыре.)
5. Отсчитайте вперед указанное количество дней ( d или остаток ⁠ д / 7 ⁠ ) с якорного дня, чтобы получить годовой.

${\begin{matrix}\left({\left\lfloor {\frac {y}{12}}\right\rfloor +y{\bmod {1}}2+\left\lfloor {\frac {y{\bmod {1}}2}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {{anchor}={\rm {Doomsday}}}}\end{matrix}}$

Например, для 1966 года двадцатого века:

${\begin{matrix}\left({\left\lfloor {\frac {66}{12}}\right\rfloor +66{\bmod {1}}2+\left\lfloor {\frac {66{\bmod {1}}2}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {Wednesday}}&=&\left(5+6+1\right){\bmod {7}}+{\rm {Wednesday}}\\\ &=&{\rm {Monday}}\end{matrix}}$

Как описано в пункте 4 выше, это эквивалентно:

${\begin{matrix}\left({66+\left\lfloor {\frac {66}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {Wednesday}}&=&\left(66+16\right){\bmod {7}}+{\rm {Wednesday}}\\\ &=&{\rm {Monday}}\end{matrix}}$

Итак, конец света в 1966 году выпал на понедельник.

Точно так же конец света в 2005 году приходится на понедельник:

$\left({\left\lfloor {\frac {5}{12}}\right\rfloor +5{\bmod {1}}2+\left\lfloor {\frac {5{\bmod {1}}2}{4}}\right\rfloor }\right){\bmod {7}}+{\rm {{Tuesday}={\rm {Monday}}}}$

Почему это работает

Правило Судного дня

Расчет опорного дня Судного дня фактически рассчитывает количество дней между любой заданной датой базового года и той же датой текущего года, а затем берет остаток по модулю 7. Когда обе даты приходятся после високосного дня (если он есть), разница всего 365 у + ⁠ y / 4 ⁠ (округляется в меньшую сторону). Но 365 равно 52 × 7 + 1, поэтому, взяв остаток, мы получаем просто

$\left(y+\left\lfloor {\frac {y}{4}}\right\rfloor \right){\bmod {7}}.$

Это дает более простую формулу, если удобно делить большие значения y на 4 и на 7. Например, мы можем вычислить

$\left(66+\left\lfloor {\frac {66}{4}}\right\rfloor \right){\bmod {7}}=(66+16){\bmod {7}}=82{\bmod {7}}=5$

что дает тот же ответ, что и в примере выше.

Значение числа 12 заключается в том, что образец ${\bigl (}y+{\bigl \lfloor }{\tfrac {y}{4}}{\bigr \rfloor }{\bigr )}{\bmod {7}}$ почти повторяется каждые 12 лет. Через 12 лет мы получим ${\bigl (}12+{\tfrac {12}{4}}{\bigr )}{\bmod {7}}=15{\bmod {7}}=1$. Если мы заменим y на y mod 12 , мы потеряем этот лишний день; но добавляя обратно ${\bigl \lfloor }{\tfrac {y}{12}}{\bigr \rfloor }$ компенсирует эту ошибку, давая окончательную формулу.

Для расчета григорианского якорного дня столетия: за тремя «общими столетиями» (каждое из которых имеют 24 високосных года) следует «високосное столетие» (имеющее 25 високосных лет). Общий век приближает конец света на

$(100+24){\bmod {7}}=2+3=5$

дней (эквивалентно двум дням назад). Високосный век переносит Судный день на 6 дней вперед (что эквивалентно одному дню назад).

Таким образом, столетия приближают конец света на

$\left(5c+{\biggl \lfloor }{c \over 4}{\biggr \rfloor }\right){\bmod {7}}$,

но это эквивалентно

$(5(c{\bmod {4}})){\bmod {7}}$.

Четыре столетия приближают конец света на

$-2-2-2-1=-7,\qquad -7\equiv 0\quad {\pmod {7}}$;

таким образом, четыре столетия образуют цикл, который оставляет Судный день неизменным (отсюда и «mod 4» в формуле века).

Метод «нечет + 11»

Простая блок-схема, показывающая метод Odd+11 для расчета опорного дня.

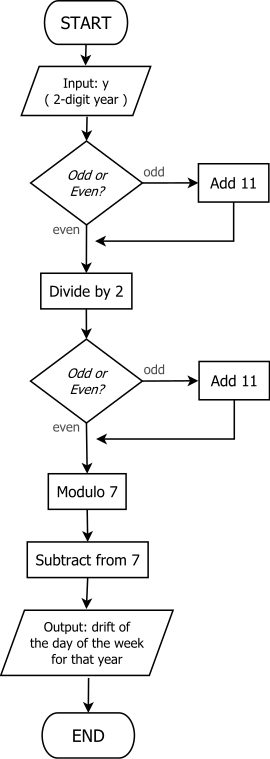
Более простой метод определения ведущего дня года был обнаружен в 2010 году Чемберленом Фонгом и Майклом К. Уолтерсом. и описаны в их статье, представленной на 7-м Международном конгрессе по промышленной и прикладной математике (2011 г.). Называется методом «нечет + 11», он эквивалентен для вычислений

$\left(y+\left\lfloor {\frac {y}{4}}\right\rfloor \right){\bmod {7}}$.

Он хорошо подходит для вычислений в уме, поскольку не требует деления на 4 (или 12), а процедуру легко запомнить благодаря многократному использованию правила «нечет + 11». Кроме того, сложение на 11 очень легко выполнить в уме при десятичной арифметике .

Расширяя это, чтобы получить опорный день, процедуру часто описывают как накопление текущего общего T за шесть шагов, а именно:

1. Пусть T — две последние цифры года.
2. Если T нечетное, добавьте 11.
3. Теперь пусть Т = ⁠ T / 2 ⁠ .
4. Если T нечетное, добавьте 11.
5. Теперь пусть T = 7 − ( T mod 7) .
6. Отсчитайте вперед T дней от опорного дня столетия, чтобы получить опорный день года.

Применяя этот метод, например, к 2005 году, шаги, описанные в общих чертах, будут следующими:

1. Т = 5
2. T = 5 + 11 = 16 (добавляем 11, потому что T нечетное)
3. Т = ⁠ 16 / 2 ⁠ = 8
4. T = 8 (ничего не делать, поскольку T четное)
5. Т = 7 - (8 по модулю 7) = 7 - 1 = 6
6. Судный день 2005 года = 6 + вторник = понедельник

Явная формула метода нечетный+11:

$7-\left[{\frac {y+11(y\,{\bmod {2}})}{2}}+11\left({\frac {y+11(y\,{\bmod {2}})}{2}}{\bmod {2}}\right)\right]{\bmod {7}}$.

Хотя это выражение выглядит устрашающим и сложным, на самом деле оно простое. из-за общего подвыражения ⁠ y + 11( y mod 2) / 2 ⁠, который нужно вычислить только один раз.

Каждый раз, когда необходимо добавить 11, вычитание 17 дает эквивалентные результаты. Хотя вычитание 17 может показаться более трудным для мысленного выполнения, чем сложение 11, бывают случаи, когда вычитание 17 проще, особенно если число представляет собой двузначное число, оканчивающееся на 7 (например, 17, 27, 37, ..., 77, 87 и 97).

Переписка с доминиальным письмом

Судный день связан с доминантной буквой года следующим образом.

Конец света	Доминическое письмо
	Високосный год	Високосный год
Воскресенье	С	округ Колумбия
Понедельник	Б	КБ
Вторник	А	НЕТ
Среда	Г	АГ
Четверг	Ф	подруга
Пятница	И	ИП
Суббота	Д	ЭД

Найдите в таблице ниже доминантную букву (DL).

Сотни лет		Д л	Остальные цифры года				#
Джулиан (р ÷ 7)	григорианский (р ÷ 4)
р5 19	16 20 р0	А	00 06   17 23	28 34   45 51	56 62   73 79	84 90	0
р4 18	15 19 р3	Г	01 07 12 18	29 35 40 46	57 63 68 74	85 91 96	1
р3 17	Н/Д	Ф	02   13 19 24	30   41 47 52	58   69 75 80	86   97	2
р2 16	18 22 р2	И	03 08 14   25	31 36 42   53	59 64 70   81	87 92 98	3
р1 15	Н/Д	Д	09 15 20 26	37 43 48 54	65 71 76 82	93 99	4
р0 14	17 21 р1	С	04 10   21 27	32 38   49 55	60 66   77 83	88 94	5
р6 13	Н/Д	Б	05 11 16 22	33 39 44 50	61 67 72 78	89 95	6

В 2024 году доминантная буква — BA + 2 = GF.

Обзор всех Судных дней

Месяц	Даты	Номера недель *
Январь (невисокосные годы)	3, 10, 17, 24, 31	1–5
Январь (високосные годы)	4, 11, 18, 25	1–4
Февраль (независимые годы)	7, 14, 21, 28	6–9
Февраль (високосные годы)	1, 8, 15, 22, 29	5–9
Маршировать	7, 14, 21, 28	10–13
апрель	4, 11, 18, 25	14–17
Может	2, 9, 16, 23, 30	18–22
Июнь	6, 13, 20, 27	23–26
Июль	4, 11, 18, 25	27–30
Август	1, 8, 15, 22, 29	31–35
Сентябрь	5, 12, 19, 26	36–39
Октябрь	3, 10, 17, 24, 31	40–44
ноябрь	7, 14, 21, 28	45–48
декабрь	5, 12, 19, 26	49–52

* В високосные годы n-й конец света приходится на ISO неделю n . В обычные годы день после n- го конца света приходится на неделю n . Таким образом, в невисокосный год номер недели в сам судный день на единицу меньше, если это воскресенье, то есть в невисокосный год, начинающийся в пятницу (например, 2010, 2021 и 2027).

Компьютерная формула опорного дня года

Для использования на компьютере удобны следующие формулы для опорного дня года.

Для григорианского календаря:

${\mbox{anchor day}}={\mbox{Tuesday}}+y+\left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor +\left\lfloor {\frac {y}{400}}\right\rfloor ={\mbox{Tuesday}}+5\times (y{\bmod {4}})+4\times (y{\bmod {1}}00)+6\times (y{\bmod {4}}00)$

Например, судный день в 2009 году приходится на субботу по григорианскому календарю (принятому в настоящее время календарю), поскольку

${\mbox{Saturday (6)}}{\bmod {7}}={\mbox{Tuesday (2)}}+2009+\left\lfloor {\frac {2009}{4}}\right\rfloor -\left\lfloor {\frac {2009}{100}}\right\rfloor +\left\lfloor {\frac {2009}{400}}\right\rfloor$

Другой пример: Судный день 1946 года приходится на четверг, поскольку

${\mbox{Thursday (4)}}{\bmod {7}}={\mbox{Tuesday (2)}}+1946+\left\lfloor {\frac {1946}{4}}\right\rfloor -\left\lfloor {\frac {1946}{100}}\right\rfloor +\left\lfloor {\frac {1946}{400}}\right\rfloor$

Для юлианского календаря:

${\mbox{anchor day}}={\mbox{Sunday}}+y+\left\lfloor {\frac {y}{4}}\right\rfloor ={\mbox{Sunday}}+5\times (y{\bmod {4}})+3\times (y{\bmod {7}})$

Формулы применимы также для пролептического григорианского календаря и пролептического юлианского календаря . Они используют функцию пола и астрономическую нумерацию лет до нашей эры.

Для сравнения см. расчет числа дней по юлианскому календарю .

400-летний цикл якорных дней

Юлианские столетия				-1600Дж -900Дж -200 Дж 500 Дж 1200Дж 1900 Дж 2600Дж 3300Дж	-1500Дж -800Дж -100 Дж 600Дж 1300Дж 2000Дж 2700Дж 3400Дж	-1400 Дж -700Дж 0Дж 700Дж 1400Дж 2100Дж 2800Дж 3500Дж	-1300Дж -600Дж 100 Дж 800Дж 1500 Дж 2200Дж 2900Дж 3600Дж	-1200Дж -500Дж 200 Дж 900Дж 1600 Дж 2300Дж 3000Дж 3700Дж	-1100Дж -400Дж 300Дж 1000Дж 1700Дж 2400Дж 3100Дж 3800Дж	-1000Дж -300 Дж 400 Дж 1100Дж 1800 Дж 2500Дж 3200Дж 3900Дж
григорианский века Годы				-1600 -1200 -800 -400 0 400 800 1200 1600 2000 2400 2800 3200 3600		-1500 -1100 -700 -300 100 500 900 1300 1700 2100 2500 2900 3300 3700		-1400 -1000 -600 -200 200 600 1000 1400 1800 2200 2600 3000 3400 3800		-1300 -900 -500 -100 300 700 1100 1500 1900 2300 2700 3100 3500 3900
00	28	56	84	Вт.	Мой.	Солнце.	Сб.	Пт.	Собирать.	Обвенчались.
01	29	57	85	Обвенчались.	Вт.	Мой.	Солнце.	Сб.	Пт.	Собирать.
02	30	58	86	Собирать.	Обвенчались.	Вт.	Мой.	Солнце.	Сб.	Пт.
03	31	59	87	Пт.	Собирать.	Обвенчались.	Вт.	Мой.	Солнце.	Сб.
04	32	60	88	Солнце.	Сб.	Пт.	Собирать.	Обвенчались.	Вт.	Мой.
05	33	61	89	Мой.	Солнце.	Сб.	Пт.	Собирать.	Обвенчались.	Вт.
06	34	62	90	Вт.	Мой.	Солнце.	Сб.	Пт.	Собирать.	Обвенчались.
07	35	63	91	Обвенчались.	Вт.	Мой.	Солнце.	Сб.	Пт.	Собирать.
08	36	64	92	Пт.	Собирать.	Обвенчались.	Вт.	Мой.	Солнце.	Сб.
09	37	65	93	Сб.	Пт.	Собирать.	Обвенчались.	Вт.	Мой.	Солнце.
10	38	66	94	Солнце.	Сб.	Пт.	Собирать.	Обвенчались.	Вт.	Мой.
11	39	67	95	Мой.	Солнце.	Сб.	Пт.	Собирать.	Обвенчались.	Вт.
12	40	68	96	Обвенчались.	Вт.	Мой.	Солнце.	Сб.	Пт.	Собирать.
13	41	69	97	Собирать.	Обвенчались.	Вт.	Мой.	Солнце.	Сб.	Пт.
14	42	70	98	Пт.	Собирать.	Обвенчались.	Вт.	Мой.	Солнце.	Сб.
15	43	71	99	Сб.	Пт.	Собирать.	Обвенчались.	Вт.	Мой.	Солнце.
16	44	72		Мой.	Солнце.	Сб.	Пт.	Собирать.	Обвенчались.	Вт.
17	45	73		Вт.	Мой.	Солнце.	Сб.	Пт.	Собирать.	Обвенчались.
18	46	74		Обвенчались.	Вт.	Мой.	Солнце.	Сб.	Пт.	Собирать.
19	47	75		Собирать.	Обвенчались.	Вт.	Мой.	Солнце.	Сб.	Пт.
20	48	76		Сб.	Пт.	Собирать.	Обвенчались.	Вт.	Мой.	Солнце.
21	49	77		Солнце.	Сб.	Пт.	Собирать.	Обвенчались.	Вт.	Мой.
22	50	78		Мой.	Солнце.	Сб.	Пт.	Собирать.	Обвенчались.	Вт.
23	51	79		Вт.	Мой.	Солнце.	Сб.	Пт.	Собирать.	Обвенчались.
24	52	80		Собирать.	Обвенчались.	Вт.	Мой.	Солнце.	Сб.	Пт.
25	53	81		Пт.	Собирать.	Обвенчались.	Вт.	Мой.	Солнце.	Сб.
26	54	82		Сб.	Пт.	Собирать.	Обвенчались.	Вт.	Мой.	Солнце.
27	55	83		Солнце.	Сб.	Пт.	Собирать.	Обвенчались.	Вт.	Мой.

Поскольку в григорианском календаре 146 097 дней, или ровно 20 871 семидневная неделя, за 400 лет якорный день повторяется каждые четыре столетия. Например, опорный день 17:00–1799 совпадает с опорным днем ​​21:00–2199, т. е. воскресенье.

Полный 400-летний цикл конца света приведен в соседней таблице. Столетия указаны для григорианского и пролептического григорианского календаря , если не отмечены буквой J для юлианского календаря. Високосные годы по григорианскому календарю выделены.

Отрицательные годы используют астрономическую нумерацию лет . Год 25 до н.э. равен -24, что показано в столбце -100J (пролептический юлианский) или -100 (пролептический григорианский) в строке 76.

Частота григорианского Судного дня в 400-летнем цикле по дням недели и типу года.

	Воскресенье	Понедельник	Вторник	Среда	Четверг	Пятница	Суббота	Общий
Невисокосные годы	43	43	43	43	44	43	44	303
Високосные годы	13	15	13	15	13	14	14	97
Общий	56	58	56	58	57	57	58	400

Високосный год, в котором понедельник является судным днем, означает, что воскресенье — один из 97 пропущенных дней в 400-летней последовательности. Таким образом, общее количество лет, в которых воскресенье является судным днем, составляет 71 минус количество високосных лет, когда понедельник является судным днем, и т. д. Поскольку понедельник как судный день пропускается в 29 февраля 2000 г., а структура високосных дней симметрична относительно этого високосного дня, частоты количество судных дней в будние дни (с добавлением обычных и високосных лет) симметрично относительно понедельника. Частота судных дней високосных лет в будние дни симметрична относительно судного дня 2000 года, вторника.

Частоту нахождения конкретной даты в определенном дне недели можно легко определить из вышеизложенного (для даты с 1 января по 28 февраля свяжите ее с судным днем ​​предыдущего года).

Например, 28 февраля — это один день после конца света предыдущего года, поэтому во вторник, четверг, воскресенье и т. д. оно повторяется по 58 раз. 29 февраля — конец света високосного года, поэтому в понедельник и среду оно повторяется по 15 раз. и т. д.

28-летний цикл

Что касается частоты конца света в юлианском 28-летнем цикле, то на каждый будний день приходится 1 високосный год и 3 обычных года, причем последний через 6, 17 и 23 года после первого (то есть с интервалами в 6, 11, 6 и 5 лет). годы распределены неравномерно, поскольку через 12 лет день в череде Судных Дней пропускается). Тот же цикл применяется к любой дате, начиная с 1 марта, приходящейся на определенный будний день.

Для любой даты до 28 февраля, приходящейся на определенный день недели, три неисчислимых года составляют 5, 11 и 22 года после високосного года, то есть с интервалами 5, 6, 11 и 6 лет. Таким образом, цикл тот же, но с 5-летним интервалом после, а не перед високосным годом.

Таким образом, для любой даты, кроме 29 февраля, интервалы между невисокосными годами, приходящимися на определенный день недели, равны 6, 11, 11. См., например, внизу страницы Невисокосный год, начинающийся в понедельник, годы в диапазоне 1906–2091.

Поскольку 29 февраля приходится на определенный будний день, он бывает только один за каждые 28 лет, и это, конечно же, високосный год.

Юлианский календарь

Григорианский календарь в настоящее время точно соответствует астрономическим событиям, таким как солнцестояния . Эта модификация юлианского календаря была впервые введена в 1582 году. Чтобы исправить дрейф календаря, 10 дней были пропущены, поэтому судный день был перенесен на 10 дней назад (т.е. на 3 дня): за четвергом 4 октября (по юлианскому календарю, судный день - среда) следовала пятница 15 октября (по григорианскому календарю, судный день - воскресенье). В таблицу включены годы по юлианскому календарю, но алгоритм предназначен только для григорианского и пролептического григорианского календаря.

Отметим, что григорианский календарь был принят не одновременно во всех странах, поэтому на протяжении многих веков в разных регионах использовались разные даты одного и того же дня.

Полные примеры

Пример 1 (1985 г.)

Предположим, мы хотим узнать день недели 18 сентября 1985 года. Начнем с опорного дня столетия, среды. К этому добавьте a , b и c выше:

• а это пол ⁠ 85/12 ⁠ , что равно 7.
• b равно 85 mod 12 , что равно 1 .
• c — пол ⁠ b / 4 ⁠ , что равно 0.

Это дает a + b + c = 8 . Отсчитав 8 дней от среды, мы достигнем четверга, который является судным днем ​​в 1985 году. (Используя числа: в арифметике по модулю 7 8 соответствует 1. Поскольку опорным днем ​​столетия является среда (индекс 3), а 3 + 1 = 4 , судный день в 1985 году был четвергом (индекс 4).) Теперь мы сравниваем 18 сентября с ближайшим судным днем, 5 сентября. Мы видим, что 18-е число приходится на 13 дней после конца света, т.е. на один день меньше двух недель. Следовательно, 18-е число было средой (днем, предшествующим четвергу). (Используя числа: в арифметике по модулю 7 13 соответствует 6 или, более кратко, -1. Таким образом, мы отнимаем единицу от конца света, четверга, и получаем, что 18 сентября 1985 года было средой.)

Пример 2 (другие века)

Предположим, мы хотим найти день недели, когда Гражданская война в США разразилась в форте Самтер , то есть 12 апреля 1861 года. 18 × 5 + ⌊ ⁠ 18/4 ​ ⌋ ⁠ ; ​или просто посмотрите на диаграмму выше, в которой перечислены опорные дни столетия). Цифры 61 обозначали смещение на шесть дней, поэтому судный день был четвергом. Следовательно, 4 апреля было четвергом, а 12 апреля, восемь дней спустя, было пятницей.

См. также

• Порядковая дата
• Computus — алгоритм Гаусса для расчета даты Пасхи
• Сравнение Целлера - алгоритм (1882 г.) для расчета дня недели для любой даты по юлианскому или григорианскому календарю.
• Ментальный расчет

Внешние ссылки

• Энциклопедия расчета дней недели Ганса-Христиана Солки, 2010 г.
• Мировые рекорды по мысленному вычислению дня недели по григорианскому календарю
• Национальные рекорды по поиску календарных дат
• Мировой рейтинг дат Memoriad Mental Calendar (все соревнования вместе взятые)
• Алгоритм Судного дня
• Находим день недели
• Стихотворение, объясняющее правило Судного дня в Wayback Machine (архивировано 18 октября 2006 г.)
• Калькулятор Судного дня на время и дату