показатель Ляпунова

Пояснения к показателю Ляпунова

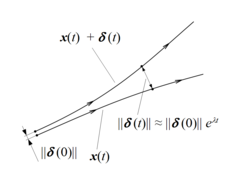
В математике показатель Ляпунова или характеристический показатель Ляпунова динамической системы — величина, характеризующая скорость разделения бесконечно малых траекторий . Количественно две траектории в фазовом пространстве с начальным вектором разделения $\delta \mathbf {Z} _{0}$ расходятся (при условии, что расхождение можно рассматривать в рамках линеаризованного приближения) со скоростью, определяемой выражением

$$|\delta \mathbf {Z} (t)|\approx e^{\lambda t}|\delta \mathbf {Z} _{0}|$$

где $\lambda$ – показатель Ляпунова.

Скорость разделения может быть различной для разных ориентаций исходного вектора разделения. Таким образом, существует спектр показателей Ляпунова , число которых равно размерности фазового пространства. Самый большой из них принято называть максимальным показателем Ляпунова (MLE), поскольку он определяет понятие предсказуемости динамической системы. системы Положительное значение MLE обычно воспринимается как признак хаотичности (при соблюдении некоторых других условий, например, компактности фазового пространства). Обратите внимание, что произвольный начальный вектор разделения обычно будет содержать некоторый компонент в направлении, связанном с MLE, и из-за экспоненциальной скорости роста влияние других показателей будет стираться с течением времени.

Экспонент носит имя Александра Ляпунова .

Определение максимального показателя Ляпунова

Максимальный показатель Ляпунова можно определить следующим образом: $$\lambda =\lim _{t\to \infty }\lim _{|\delta \mathbf {Z} _{0}|\to 0}{\frac {1}{t}}\ln {\frac {|\delta \mathbf {Z} (t)|}{|\delta \mathbf {Z} _{0}|}}$$

Предел $|\delta \mathbf {Z} _{0}|\to 0$ обеспечивает справедливость линейного приближенияв любое время.

Для системы дискретного времени (карты или итерации с фиксированной точкой) $x_{n+1}=f(x_{n})$, для орбиты, начинающейся с $x_{0}$ это переводится как: $$\lambda (x_{0})=\lim _{n\to \infty }{\frac {1}{n}}\sum _{i=0}^{n-1}\ln |f'(x_{i})|$$

Определение спектра Ляпунова

Ведущий вектор Ляпунова.

Для динамической системы с уравнением эволюции ${\dot {x}}_{i}=f_{i}(x)$ в n –мерном фазовом пространстве спектр показателей Ляпунова $$\{\lambda _{1},\lambda _{2},\ldots ,\lambda _{n}\}\,,$$в общем, зависит от отправной точки $x_{0}$. Однако нас обычно будет интересовать аттрактор (или аттракторы) динамической системы, и с каждым аттрактором обычно связан один набор показателей степени. Выбор начальной точки может определить, на каком аттракторе окажется система, если их несколько. (Для гамильтоновых систем, не имеющих аттракторов, это не проблема.) Показатели Ляпунова описывают поведение векторов в касательном пространстве фазового пространства и определяются из матрицы Якобиана $$J_{ij}(t)=\left.{\frac {df_{i}(x)}{dx_{j}}}\right|_{x(t)}$$этот якобиан определяет эволюцию касательных векторов, заданную матрицей $Y$, через уравнение $${\dot {Y}}=JY$$с начальным состоянием $Y_{ij}(0)=\delta _{ij}$. Матрица $Y$ описывает, как небольшое изменение в точке $x(0)$ распространяется до конечной точки $x(t)$. Предел $$\Lambda =\lim _{t\rightarrow \infty }{\frac {1}{2t}}\log(Y(t)Y^{T}(t))$$определяет матрицу $\Lambda$ (условия существования предела даются теоремой Оселедца ). Показатели Ляпунова $\lambda _{i}$ определяются собственными значениями $\Lambda$.

Набор показателей Ляпунова будет одинаковым почти для всех стартовых точек эргодической компоненты динамической системы.

Показатель Ляпунова для нестационарной линеаризации

Чтобы ввести показатель Ляпунова, рассмотрим фундаментальную матрицу $X(t)$ (например, для линеаризации вдоль стационарного решения $x_{0}$ в непрерывной системе) фундаментальная матрица равна $\exp \left(\left.{\frac {df^{t}(x)}{dx}}\right|_{x_{0}}t\right)$ состоящее из линейно независимых решений первого порядка приближения системы. Сингулярные значения $\{\alpha _{j}{\big (}X(t){\big )}\}_{1}^{n}$ матрицы $X(t)$ являются квадратными корнями собственных значений матрицы $X(t)^{*}X(t)$.Самый крупный показатель Ляпунова $\lambda _{\mathrm {max} }$ заключается в следующем $$\lambda _{\mathrm {max} }=\max \limits _{j}\limsup _{t\rightarrow \infty }{\frac {1}{t}}\ln \alpha _{j}{\big (}X(t){\big )}.$$Ляпунов доказал, что если система первого приближения регулярна (например, все системы с постоянными и периодическими коэффициентами регулярны) и ее наибольший показатель Ляпунова отрицателен, то решение исходной системы асимптотически устойчиво по Ляпунову .Позднее О. Перрон заявил, что требование регулярности первого приближения существенно.

Эффекты Перрона при инверсии знака наибольшего показателя Ляпунова

В 1930 г. О. Перрон построил пример системы второго порядка, в которой первое приближение имеет отрицательные показатели Ляпунова вдоль нулевого решения исходной системы, но в то же время это нулевое решение исходной нелинейной системы является неустойчивым по Ляпунову. Более того, в некоторой окрестности этого нулевого решения почти все решения исходной системы имеют положительные показатели Ляпунова. Также можно построить обратный пример, в котором первое приближение имеет положительные показатели Ляпунова вдоль нулевого решения исходной системы, но в то же время это нулевое решение исходной нелинейной системыЛяпунов стабилен. В дальнейшем был изучен эффект инверсии знака показателей Ляпунова решений исходной системы и системы первого приближения с теми же начальными данными.называется эффектом Перрона.

Контрпример Перрона показывает, что отрицательный наибольший показатель Ляпунова, как правило, не указывает на стабильность, и чтоположительный наибольший показатель Ляпунова, как правило, не указывает на хаос.

Поэтому нестационарная линеаризация требует дополнительного обоснования.

Основные свойства

Если система консервативна (т. е. в ней нет диссипации ), элемент объема фазового пространства будет оставаться неизменным вдоль траектории. Таким образом, сумма всех показателей Ляпунова должна быть равна нулю. Если система диссипативна, сумма показателей Ляпунова отрицательна.

Если система является потоком и траектория не сходится к одной точке, один показатель всегда равен нулю — показатель Ляпунова, соответствующий собственному значению $L$ с собственным вектором по направлению потока.

Значение спектра Ляпунова

Спектр Ляпунова можно использовать для оценки скорости производства энтропии.фрактальной размерности и хаусдорфовой размерности рассматриваемой динамической системы . В частности, из знания спектра Ляпунова можно получить так называемую размерность Ляпунова (или размерность Каплана – Йорка ) $D_{KY}$, который определяется следующим образом: $$D_{KY}=k+\sum _{i=1}^{k}{\frac {\lambda _{i}}{|\lambda _{k+1}|}}$$где $k$ — максимальное целое число такое, что сумма $k$ наибольшие показатели по-прежнему неотрицательны. $D_{KY}$ представляет собой верхнюю границу информационного измерения системы. Более того, сумма всех положительных показателей Ляпунова дает оценку энтропии Колмогорова – Синая в соответствии с теоремой Песина. Наряду с широко используемыми численными методами оценки и вычисления размерности Ляпунова существует эффективный аналитический подход, основанный на прямом методе Ляпунова со специальными функциями типа Ляпунова. Показатели Ляпунова ограниченной траектории и размерность Ляпунова аттрактора инвариантны относительно диффеоморфизма фазового пространства.

Мультипликативный обратный наибольшему показателю Ляпунова иногда называют в литературе временем Ляпунова и определяет характерное e время -свертывания. Для хаотических орбит время Ляпунова будет конечным, тогда как для регулярных орбит оно будет бесконечным.

Численный расчет

Точки внутри и снаружи множества Мандельброта, раскрашенные показателем Ляпунова.

Как правило, расчет показателей Ляпунова, определенных выше, не может быть выполнен аналитически, и в большинстве случаев приходится прибегать к численным методам. Ранний пример, который также представляет собой первую демонстрацию экспоненциального расхождения хаотических траекторий, был проведен Р. Х. Миллером в 1964 году. В настоящее время наиболее часто используемая численная процедура оценивает $L$ матрица, основанная на усреднении нескольких аппроксимаций за конечное время предела, определяющего $L$.

Один из наиболее используемых и эффективных численных методов расчета спектра Ляпунова для гладкой динамической системы основан на периодической Грама – Шмидта ортонормировке векторов Ляпунова , чтобы избежать рассогласования всех векторов в направлении максимального расширения. Описан спектр Ляпунова различных моделей. Представлены исходные коды для нелинейных систем, таких как отображение Энона, уравнения Лоренца, дифференциальное уравнение с запаздыванием и т. д.

Для расчета показателей Ляпунова по ограниченным экспериментальным данным были предложены различные методы. Однако применение этих методов сопряжено с множеством трудностей, и к таким проблемам следует подходить с осторожностью. Основная трудность заключается в том, что данные не полностью исследуют фазовое пространство, а ограничиваются аттрактором, который имеет очень ограниченное (если таковое имеется) расширение в определенных направлениях. Эти более тонкие или более сингулярные направления в наборе данных связаны с более отрицательными показателями. Было показано, что использование нелинейных отображений для моделирования эволюции малых смещений от аттрактора значительно улучшает способность восстановления спектра Ляпунова. при условии, что данные имеют очень низкий уровень шума. Также был исследован исключительный характер данных и их связь с более отрицательными показателями.

Локальный показатель Ляпунова

В то время как (глобальный) показатель Ляпунова дает меру полной предсказуемости системы, иногда представляет интерес оценить локальную предсказуемость вокруг точки x ₀ в фазовом пространстве. Это можно сделать через значения матрицы Якоби J собственные ⁰ ( х ₀ ) . Эти собственные значения также называются локальными показателями Ляпунова. Локальные показатели степени не инвариантны относительно нелинейной замены координат.

Условный показатель Ляпунова

Этот термин обычно используется в отношении синхронизации хаоса , в которой есть две системы, которые связаны, обычно однонаправленно, так что есть приводная (или ведущая) система и ответная (или ведомая) система. Условные показатели — это показатели системы реагирования, в которой система возбуждения рассматривается просто как источник (хаотического) сигнала возбуждения. Синхронизация происходит, когда все условные показатели отрицательны.

См. также

• Теория Хаоса
• Хаотическое смешивание для альтернативного вывода
• Гипотеза Идена о размерности Ляпунова
• Теория Флоке
• Теорема Лиувилля (гамильтониан)
• Ляпуновское измерение
• Ляпуновское время
• Количественный анализ рецидивов
• Oseledets theorem
• Эффект бабочки

Дальнейшее чтение

• Кузнецов, Николай; Райтманн, Волкер (2020). Оценки размерности аттрактора для динамических систем: теория и вычисления . Чам: Спрингер.
• М.-Ф. Данка и Н.В. Кузнецов (2018). «Код Matlab для показателей Ляпунова систем дробного порядка». Международный журнал бифуркации и хаоса . 25 (5): 1850067–1851392. arXiv : 1804.01143 . Бибкод : 2018IJBC...2850067D . дои : 10.1142/S0218127418500670 .
• Цвитанович П., Артузо Р., Майниери Р., Таннер Г. и Ваттай Г. Хаос: классический и квантовый Институт Нильса Бора, Копенгаген, 2005 г. - учебник о хаосе, доступный по лицензии свободной документации.
• Фредди Кристиансен и Ханс Хенрик Руг (1997). «Расчет спектров Ляпунова с непрерывной ортонормировкой Грама – Шмидта» . Нелинейность . 10 (5): 1063–1072. arXiv : чао-дин/9611014 . Бибкод : 1997Nonli..10.1063C . дои : 10.1088/0951-7715/10/5/004 . S2CID   122976405 . Архивировано из оригинала 25 апреля 2006 г.
• Салман Хабиб и Роберт Д. Райн (1995). «Симплектическое вычисление показателей Ляпунова». Письма о физических отзывах . 74 (1): 70–73. arXiv : чао-дин/9406010 . Бибкод : 1995PhRvL..74...70H . doi : 10.1103/PhysRevLett.74.70 . ПМИД   10057701 . S2CID   19203665 .
• Говиндан Рангараджан; Салман Хабиб и Роберт Д. Райн (1998). «Показатели Ляпунова без масштабирования и реортогонализации». Письма о физических отзывах . 80 (17): 3747–3750. arXiv : чао-дин/9803017 . Бибкод : 1998PhRvL..80.3747R . doi : 10.1103/PhysRevLett.80.3747 . S2CID   14483592 .
• С. Цзэн; Р. Эйхольт и Р. А. Пилке (1991). «Оценка спектра показателя Ляпунова по коротким временным рядам низкой точности». Письма о физических отзывах . 66 (25): 3229–3232. Бибкод : 1991PhRvL..66.3229Z . дои : 10.1103/PhysRevLett.66.3229 . ПМИД   10043734 .
• Э. Аурел; Дж. Боффетта; Крисанти; Г Паладин; Вульпиани (1997). «Предсказуемость в целом: расширение понятия показателя Ляпунова». Дж. Физ. А: Математика. Ген . 30 (1): 1–26. arXiv : чао-дин/9606014 . Бибкод : 1997JPhA...30....1A . дои : 10.1088/0305-4470/30/1/003 . S2CID   54697488 .
• Ф. Джинелли; П. Поджи; Турчи; Х. Шатэ; Р Ливи; Полити (2007). «Характеристика динамики с помощью ковариантных векторов Ляпунова» (PDF) . Письма о физических отзывах . 99 (13): 130601. arXiv : 0706.0510 . Бибкод : 2007PhRvL..99m0601G . doi : 10.1103/PhysRevLett.99.130601 . hdl : 2158/253565 . ПМИД   17930570 . S2CID   21992110 . Архивировано из оригинала (PDF) 31 октября 2008 г.

Программное обеспечение

• [1] Р. Хеггер, Х. Канц и Т. Шрайбер, Нелинейный анализ временных рядов, TISEAN 3.0.1 (март 2007 г.).
• [2] Продукт ChaosKit от Scientio вычисляет показатели Ляпунова среди других хаотических мер. Доступ предоставляется онлайн через веб-службу и демо-версию Silverlight.
• [3] Архивировано 28 июня 2022 г. в Wayback Machine. Лаборатория программного обеспечения для математических развлечений доктора Рональда Джо Рекорда включает в себя графический клиент X11, lyap, для графического исследования показателей Ляпунова принудительной логистической карты и других карт единичного интервала. Также доступны содержимое и страницы руководства лаборатории программного обеспечения mathrec.
• [4] Программное обеспечение на этой странице было разработано специально для эффективного и точного расчета полного спектра показателей. Сюда входит LyapOde для случаев, когда уравнения движения известны, а также Lyap для случаев, связанных с экспериментальными данными временных рядов. LyapOde, включающий в себя исходный код, написанный на «C», также умеет вычислять условные показатели Ляпунова для связанных идентичных систем. Он предназначен для того, чтобы позволить пользователю предоставить свой собственный набор уравнений модели или использовать одно из включенных. Никаких ограничений на количество переменных, параметров и т. д. нет. Ляп, включающий исходный код, написанный на Фортране, также может рассчитывать векторы направления Ляпунова и характеризовать сингулярность аттрактора, что является основной причиной трудностей при вычислении более отрицательные показатели из данных временных рядов. В обоих случаях имеется обширная документация и примеры входных файлов. Программное обеспечение можно скомпилировать для работы в системах Windows, Mac или Linux/Unix. Программное обеспечение работает в текстовом окне и не имеет графических возможностей, но может генерировать выходные файлы, которые можно легко построить с помощью такой программы, как Excel.

Внешние ссылки

• Перроновы эффекты инверсии знака показателя Ляпунова