Приближенно конечномерная C*-алгебра

В математике приближенно конечномерная (AF) C*-алгебра это C*-алгебра , которая является индуктивным пределом последовательности — конечномерных C * -алгебр. Приближенная конечномерность была впервые определена и описана комбинаторно Олой Браттели . Позже Джордж А. Эллиотт дал полную классификацию алгебр AF, используя функтор K ₀ , диапазон которого состоит из упорядоченных абелевых групп с достаточно хорошей порядковой структурой.

Теорема классификации AF-алгебр служит прототипом результатов классификации для более крупных классов сепарабельных простых аменабельных стабильно конечных C*-алгебр. Его доказательство делится на две части. Инвариантом здесь является K ₀ с его структурой естественного порядка; это функтор . Сначала доказывается существование : гомоморфизм между инвариантами должен подниматься до *-гомоморфизма алгебр. Во-вторых, доказывается уникальность : подъем должен быть уникальным с точностью до приблизительной унитарной эквивалентности. Классификация тогда следует из так называемого переплетающегося аргумента . Для унитальных алгебр AF как существование, так и единственность следуют из того факта, что полугруппа проекций Мюррея-фон Неймана в алгебре AF сократима.

Аналогом простых AF C*-алгебр в мире алгебр фон Неймана являются гиперконечные факторы, которые были классифицированы Конном и Хаагерупом .

В контексте некоммутативной геометрии и топологии обобщениями C0 _{AF C*-алгебры являются некоммутативными} ( X ), где X — вполне несвязное метризуемое пространство.

Определение и основные свойства

Конечномерные C*-алгебры

Произвольная конечномерная С*-алгебра А с точностью до изоморфизма принимает следующий вид:

\oplus _{k}M_{n_{k}},

где M _i обозначает полную матричную алгебру матриц размера i × i .

до унитарной эквивалентности унитальный *-гомоморфизм Φ : → _Mi Mj обязательно _{С точностью} имеет вид

\Phi (a)=a\otimes I_{r},

где р · я знак равно j . Число r называется кратностью Φ. В общем случае, гомоморфизм с единицей между конечномерными C*-алгебрами

\Phi :\oplus _{1}^{s}M_{n_{k}}\rightarrow \oplus _{1}^{t}M_{m_{l}}

задается с точностью до унитарной эквивалентности матрицей × s частичной t кратности ( r _{l k} ), удовлетворяющей для всех l

\sum _{k}r_{lk}n_{k}=m_{l}.\;

В неединичном случае равенство заменяется на ≤. Графически Φ, что эквивалентно ( r _{l k} ), может быть представлена ее диаграммой Браттели . Диаграмма Браттели представляет собой ориентированный граф с узлами, соответствующими каждому n _k и m _l, а число стрелок от n _k до m _l представляет собой частичную кратность r _lk .

Рассмотрим категорию, объектами которой являются классы изоморфизма конечномерных С*-алгебр, а морфизмами которой являются *-гомоморфизмы по модулю унитарной эквивалентности. Согласно приведенному выше обсуждению, объекты можно рассматривать как векторы с элементами в N , а морфизмы — это матрицы частичной кратности.

алгебры

AC*-алгебра называется AF , если она является прямым пределом последовательности конечномерных C*-алгебр:

A=\varinjlim \cdots \rightarrow A_{i}\,{\stackrel {\alpha _{i}}{\rightarrow }}A_{i+1}\rightarrow \cdots ,

где каждое A _i — конечномерная C*-алгебра, а связующие отображения α _i — *-гомоморфизмы. Будем считать, что каждое α _i единично. Индуктивная система, задающая алгебру АФ, не единственна. Всегда можно перейти к подпоследовательности. Подавив соединительные карты, A также можно записать как

A={\overline {\cup _{n}A_{n}}}.

Диаграмма Браттели оператора A формируется из диаграмм Браттели элемента { α _i } очевидным образом. Например, треугольник Паскаля с узлами, соединенными соответствующими стрелками вниз, представляет собой диаграмму Браттели алгебры AF. диаграмма Браттели алгебры CAR Справа представлена . Две стрелки между узлами означают, что каждая соединительная карта является вложением кратности 2.

1\rightrightarrows 2\rightrightarrows 4\rightrightarrows 8\rightrightarrows \dots

(Диаграмма Браттели алгебры CAR)

Если алгебра АФ A = (∪ _n A _n ) ⁻ идеал J в A принимает вид ∪ _n ( J ∩ An ₎, то ⁻. В частности, J сама является алгеброй AF. Учитывая диаграмму Браттели A и некоторое подмножество S узлов, поддиаграмма, порожденная S, дает индуктивную систему, которая задает идеал A . Фактически, каждый идеал возникает таким образом.

Благодаря наличию матричных единиц в индуктивной последовательности алгебры AF имеют следующую локальную характеризацию: C*-алгебра A является AF тогда и только тогда, когда A сепарабельна и любое конечное подмножество A «почти содержится» в некотором конечном размерная C*-подалгебра.

Проекции в ∪ _An фактически _{образуют} приблизительную единицу A . n

Ясно, что расширение конечномерной С*-алгебры другой конечномерной С*-алгеброй снова конечномерно. В более общем смысле расширение алгебры AF с помощью другой алгебры AF снова является AF. ^[1]

Классификация

до ₀

K -теоретико- K0 является _группа инвариантом C*-алгебр. Она берет свое начало в топологической К-теории и служит диапазоном своего рода «функции размерности». алгебры AF A Для K ₀ ( A ) можно определить следующим образом.Пусть M _n ( A ) — C*-алгебра матриц размера n × n, элементы которой являются элементами A . M _n ( A ) можно вложить в M _{n + 1} ( A ) канонически, в «левый верхний угол». Рассмотрим алгебраический прямой предел

M_{\infty }(A)=\varinjlim \cdots \rightarrow M_{n}(A)\rightarrow M_{n+1}(A)\rightarrow \cdots .

Обозначим проекции (самосопряженные идемпотенты) в этой алгебре через P ( A ). Два элемента p и q называются эквивалентными по Мюррею-фон Нейману и обозначаются p ~ q , если p = vv* и q = v*v для некоторой частичной изометрии v в M _∞ ( A ). Ясно, что ~ — отношение эквивалентности. Определим бинарную операцию + на множестве эквивалентностей P ( A )/~ с помощью

[p]+[q]=[p\oplus q]

где ⊕ дает ортогональную прямую сумму двух конечномерных матриц, соответствующих p и q . Хотя мы могли бы выбрать матрицы сколь угодно большой размерности для замены p и q , наш результат в любом случае будет эквивалентным. Это делает P ( A )/~ полугруппой , обладающей свойством сокращения . Обозначим эту полугруппу через K ₀ ( A ) ⁺. Выполнение построения группы Гротендика дает абелеву группу K ₀ ( A ).

K ₀ ( A ) имеет структуру естественного порядка: мы говорим [ p ] ≤ [ q ], если p эквивалентен по Мюррею-фон Нейману подпроекции q . Это делает K0 _, ( A ) упорядоченной группой положительный конус которой равен ( _K0 A ) . ⁺.

Например, для конечномерной С*-алгебры

A=\oplus _{k=1}^{m}M_{n_{k}},

у одного есть

(K_{0}(A),K_{0}(A)^{+})=(\mathbb {Z} ^{m},\mathbb {Z} _{+}^{m}).

Двумя существенными особенностями отображения A ↦ K ₀ ( A ) являются:

K ₀ — (ковариантный) функтор . *-гомоморфизм α : A → B между алгебрами AF индуцирует групповой гомоморфизм α _* : K ₀ ( A ) → K ₀ ( B ). В частности, когда A и B оба конечномерны, α _* можно отождествить с матрицей частичных кратностей α .
K ₀ соблюдает прямые ограничения. Если А знак равно ∪ _п α _п ( А _п ) ⁻, то K ₀ ( A ) — прямой предел ∪ _n α _{n *} ( K ₀ ( A _n )).

Группа измерений

Поскольку M∞ _{точностью} ( M∞ _может ( A изоморфно M∞ ₍ ) ) A ), K0 _{различать алгебры AF только с} до стабильного изоморфизма . Например, М ₂ и М ₄ не изоморфны, а стабильно изоморфны; K ₀ ( M ₂ ) знак равно K ₀ ( M ₄ ) знак равно Z .

Для обнаружения классов изоморфизма необходим более тонкий инвариант. Для алгебры AF A мы определяем масштаб K 0 _{), как подмножество ,} ( A ), обозначаемый Γ( A элементы которого представлены проекциями в A :

\Gamma (A)=\{[p]\,|\,p^{*}=p^{2}=p\in A\}.

Когда A унитален с единицей 1 _A , элемент K ₀ [1 _A ] является максимальным элементом Γ( A ) и фактически

\Gamma (A)=\{x\in K_{0}(A)\,|\,0\leq x\leq [1_{A}]\}.

Тройка ( K ₀ , K ₀⁺, Γ( ) ) называется группой размерностей A . A Если A = M _s , его группа размерностей равна ( Z , Z ⁺, {1, 2,..., с }).

Групповой гомоморфизм между группами размерностей называется сжимающим , если он сохраняет масштаб. Двумерная группа называется изоморфной, если между ними существует сжимающий групповой изоморфизм.

Размерная группа сохраняет существенные свойства К ₀ :

*-гомоморфизм α : A → B между алгебрами AF фактически индуцирует гомоморфизм сжимающих групп α _* на группах размерностей. Когда A и B оба конечномерны и соответствуют каждой матрице частичных кратностей ψ , существует единственный с точностью до унитарной эквивалентности *-гомоморфизм α : A → B такой, что α _* = ψ .
Если А знак равно ∪ _п α _п ( А _п ) ⁻, то группа размерностей A является прямым пределом групп An _{размерностей} .

Теорема Эллиотта

Теорема Эллиотта утверждает, что группа размерностей является полным инвариантом алгебр AF: две алгебры AF A и B изоморфны тогда и только тогда, когда их группы размерностей изоморфны.

Прежде чем можно будет набросать доказательство теоремы Эллиотта, необходимы два предварительных факта. Первый из них подводит итог вышеизложенному обсуждению конечномерных C*-алгебр.

Лемма Для двух конечномерных C*-алгебр A и B и сжимающего гомоморфизма ψ : K ₀ ( A ) → K ₀ ( B ) существует *-гомоморфизм φ : A → B такой, что φ _* = ψ , и φ единственна с точностью до унитарной эквивалентности.

Лемму можно распространить на случай, когда B есть AF. Отображение ψ на уровне K ₀ можно «переместить назад», на уровне алгебр, на некоторую конечную ступень индуктивной системы.

Лемма. Пусть A конечномерен и B AF, B = (∪ _n B _n ) ⁻. Пусть βm _— канонический Bm в B. гомоморфизм Тогда для любого сжимающего гомоморфизма ψ : K ₀ ( A ) → K ₀ ( B ) существует *-гомоморфизм φ : A → B _m такой, что β _m* φ _* = ψ , и φ единственен с точностью до унитарной эквивалентности. в Б.

Доказательство леммы основано на простом наблюдении, что K ₀ ( A ) конечно порождено и, поскольку K ₀ подчиняется прямым пределам, K ₀ ( B ) = ∪ _n β _n* K ₀ ( B _n ).

Теорема (Эллиотта) Две алгебры AF A и B изоморфны тогда и только тогда, когда их группы размерностей ( K ₀ ( A ), K ₀⁺( A ), Γ( A )) и ( K ₀ ( B ), K ₀⁺( B ), Γ( B )) изоморфны.

Суть доказательства стала известна как переплетающийся аргумент Эллиотта . Учитывая изоморфизм между группами размерностей, можно построить диаграмму коммутирующих треугольников между прямыми системами A и B, применяя вторую лемму.

Наметим доказательство нетривиальной части теоремы, соответствующей последовательности коммутативных диаграмм справа.

Полет Φ: ( К ₀ ( А ), К ₀⁺( А ), Γ( ) ) → ( K ₀ ( B ), K _А⁺( B ), Γ( B )) — изоморфизм группы размерностей.

Рассмотрим композицию отображений Φ α _1* : K ₀ ( A ₁ ) → K ₀ ( B ). По предыдущей лемме существуют B ₁ и *-гомоморфизм φ ₁ : A ₁ → B ₁ такие, что первая диаграмма справа коммутирует.
Тот же аргумент применим к β _1* Φ ⁻¹ показывает, что вторая диаграмма коммутирует для некоторого A ₂ .
Сравнивая диаграммы 1 и 2, получаем диаграмму 3.
Используя свойство прямого предела и перемещая A ₂ при необходимости дальше вниз, получаем диаграмму 4 — коммутативный треугольник на уровне K ₀ .
Для конечномерных алгебр два *-гомоморфизма индуцируют одно и то же отображение на тогда _K0 и только тогда, когда они унитарно эквивалентны. Итак, составив при необходимости ψ ₁ с унитарным сопряжением, мы имеем коммутативный треугольник на уровне алгебр.
По индукции мы имеем диаграмму коммутирующих треугольников, указанную на последней диаграмме. Отображение φ : A → B является прямым пределом последовательности { φ _n }. Пусть ψ : B → A — прямой предел последовательности { ψ _n }. Ясно, что φ и ψ взаимно обратны. Следовательно, A и B изоморфны.

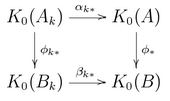
, на уровне K0 _{Более того} соседняя диаграмма коммутирует для каждого k . В силу единственности прямого предела отображений ф _* = Ф.

Теорема Эффроса-Хендельмана-Шена

Группа размерностей алгебры AF является группой Рисса . Теорема Эффроса-Хендельмана-Шена утверждает, что верно обратное. Каждая группа Рисса заданного масштаба возникает как группа размерностей некоторой алгебры AF. Это задает диапазон классифицирующего функтора K ₀ для AF-алгебр и завершает классификацию.

Группы Рисса

Группа G с частичным порядком называется упорядоченной группой . Набор G ⁺ 0 называется положительным конусом G . элементов ≥ Говорят, что группа G неперфорирована, если k · g ∈ G ⁺ подразумевает g ∈ G ⁺.

Следующее свойство называется свойством разложения Рисса : если x , yi _x ≥ 0 и ⩽ Σ y _i , то существует x _i ≥ 0 такой, что x = Σ x _i и x _i ⩽ y _i для каждого i .

Группа Рисса ( G , G ⁺) — упорядоченная группа, неперфорированная и обладающая свойством разложения Рисса.

Ясно, что если A конечномерен, ( K ₀ , K ₀⁺) — группа Рисса, где Z ^к дан по входному порядку. Два свойства групп Рисса сохраняются в прямых пределах, если предположить, что структура порядка в прямом пределе происходит из структур индуктивной системы. Итак ( К ₀ , К ₀⁺) — группа Рисса для алгебры AF A .

Ключевым шагом на пути к теореме Эффроса-Хендельмана-Шена является тот факт, что каждая группа Рисса является прямым пределом Z ^к каждый из которых имеет каноническую структуру порядка. иногда называют критерием Шена Это зависит от следующей технической леммы, которую в литературе .

Критерий Шена.

Лемма Пусть ( G , G ⁺) — группа Рисса, φ : ( Z ^к, С ^к₊) → ( G , G ⁺) — положительный гомоморфизм. Тогда существуют отображения σ и ψ , как указано на соседней диаграмме, такие, что ker( σ ) = ker( φ ).

Следствие. Любая группа Рисса ( G , G ⁺) можно выразить как прямой предел

(G,G^{+})=\varinjlim (\mathbb {Z} ^{n_{k}},\mathbb {Z} _{+}^{n_{k}}),

где все связующие гомоморфизмы в ориентированной системе в правой части положительны.

Теорема

Теорема Если ( G , G ⁺) — счетная группа Рисса масштаба Γ( G ), то существует алгебра AF A такая, что ( K ₀ , K ₀⁺, Γ( А )) знак равно ( грамм , грамм ⁺, Γ( G )). В частности, если Γ( G ) = [0, u _G ] с максимальным элементом u _G , то A унитальна с [1 _A ] = [ u _G ].

Рассмотрим сначала специальный случай, когда Γ( ) = [0, uG _] с максимальным элементом uG _G . Предполагать

(G,G^{+})=\varinjlim (H_{k},H_{k}^{+}),\quad {\mbox{where}}\quad (H,H_{k}^{+})=(\mathbb {Z} ^{n_{k}},\mathbb {Z} _{+}^{n_{k}}).

Переходя к подпоследовательности, если необходимо, пусть

\Gamma (H_{1})=\{v\in H_{1}^{+}|\phi _{1}(v)\in \Gamma (G)\},

где φ ₁ ( ты ₁ ) знак равно ты _G для некоторого элемента ты ₁ . Теперь рассмотрим идеал порядка G _1, порожденный u ₁ . Поскольку каждый H ₁ имеет структуру канонического порядка, G ₁ представляет собой прямую сумму Z (с возможным количеством копий меньше, чем в H ₁ ). Таким образом, это дает конечномерную алгебру A ₁ , группа размерностей которой равна ( G ₁ G ₁⁺, [0, u ₁ ]). Затем переместите u ₁ вперед, определив u ₂ = φ ₁₂ ( u ₁ ). И снова u ₂ определяет конечномерную алгебру A ₂ . Существует соответствующий гомоморфизм α ₁₂ такой, что α _12* = φ ₁₂ . Индукция дает направленную систему

A=\varinjlim A_{k},

чье K ₀

\varinjlim (G_{k},G_{k}^{+}),

с масштабом

\cup _{k}\phi _{k}[0,u_{k}]=[0,u_{G}].

Это доказывает частный случай.

Аналогичный аргумент применим и в целом. Заметьте, что шкала по определению является ориентированным множеством . Если Γ( G ) = { v _k }, можно выбрать u _k ∈ Γ( G ) так, что u _k ≥ v ₁ ... v _k . Те же рассуждения, что и выше, доказывают теорему.

Примеры

По определению равномерно гиперконечные алгебры AF и унитальны. Их группы размерностей являются подгруппами Q . Например, для матриц M ₂ размера 2 × 2 K ₀ ( M ₂ ) — это группа рациональных чисел вида ⁠ a / 2 ⁠ для a в Z . Масштаб: Γ( M ₂ ) = {0, ⁠ 1/2 ⁠ 1 , }. Для CAR-алгебры A 0 K ₀ ( A ) — это группа рациональных чисел масштаба K _{двоично -} ( A ) ∩ [0, 1], при этом 1 = [1 _A ]. Все такие группы просты в смысле, соответствующем упорядоченным группам. Таким образом, алгебры СВФ являются простыми С*-алгебрами. В общем случае группы, не плотные в Q, группами размерности Mk _{являются} для некоторого k .

Коммутативные С*-алгебры, охарактеризованные Гельфандом , являются АФ именно тогда, когда спектр несвязен полностью . ^[2] Непрерывные функции C ( X ) на канторовом множестве X являются одним из таких примеров.

Программа классификации Эллиотта

Эллиотт предположил, что другие классы C*-алгебр могут быть классифицированы с помощью K-теоретико-инвариантов. Для C*-алгебры A определяется инвариант Эллиотта как

{\mbox{Ell}}(A)=((K_{0}(A),K_{0}(A)^{+},\Gamma (A)),K_{1}(A),T^{+}(A),\rho _{A}),

где $T^{+}(A)$ — следовые положительные линейные функционалы в топологии слабого*, а $\rho _{A}$ является естественным сочетанием между $T^{+}(A)$ и $K_{0}(A)$ .

Исходная гипотеза Эллиотта утверждала, что инвариант Эллиотта классифицирует простые сепарабельные аменабельные C*-алгебры с единицей.

В литературе можно встретить несколько гипотез такого рода с соответствующими модифицированными/уточненными инвариантами Эллиотта.

Алгебры фон Неймана

В соответствующем контексте приблизительно конечномерная или гиперконечная алгебра фон Неймана — это алгебра с сепарабельным предуалом и содержит слабо плотную AF C*-алгебру. Мюррей и фон Нейман показали, что с точностью до изоморфизма существует единственный гиперконечный _{типа II 1} фактор . Конн получил аналогичный результат для фактора II _∞ . Пауэрс продемонстрировал семейство неизоморфных гиперконечных факторов типа III с мощностью континуума. Сегодня у нас есть полная классификация гиперконечных факторов.

Примечания

^ Лоуренс Г. Браун. Расширения алгебр AF: проблема поднятия проекций. Операторные алгебры и приложения, Труды симпозиумов по чистой математике, вып. 38, часть 1, стр. 175–176, Американская математическая общество, 1982 г.
^ Дэвидсон 1996, с. 77.

Ссылки

Браттели, Ола. (1972), Индуктивные пределы конечномерных C*-алгебр , Тран. амер. Математика. Соц. 171 , 195-234.
Дэвидсон, К.Р. (1996), C*-алгебры на примерах , Монографии Полевого института 6 , Американское математическое общество.
Эффрос Э.Г. , Хандельман Д.Э. и Шен К.Л. (1980), Группы размерностей и их аффинные представления , Amer. Дж. Математика. 102 , 385-402.
Эллиотт, Джорджия (1976), О классификации индуктивных пределов последовательностей полупростых конечномерных алгебр , J. Algebra 38 , 29-44.
Эллиотт Г.А. и Томс А.С. (2008), Свойства регулярности в программе классификации сепарабельных аменабельных C-алгебр , Bull. амер. Математика. Соц. 45 , 229-245.
Филлмор, Пенсильвания (1996), Руководство пользователя по операторным алгебрам , Wiley-Interscience.
Рёрдам, М. (2002), Классификация ядерных C*-алгебр , Энциклопедия математических наук 126 , Springer-Verlag.

Внешние ссылки

«АФ-алгебра» , Математическая энциклопедия , EMS Press , 2001 [1994]

[1] Лоуренс Г. Браун. Расширения алгебр AF: проблема поднятия проекций. Операторные алгебры и приложения, Труды симпозиумов по чистой математике, вып. 38, часть 1, стр. 175–176, Американская математическая общество, 1982 г.

[2] Дэвидсон 1996, с. 77.

[1]

[2]