Оптическая аберрация

1: Изображение линзой с хроматической аберрацией . 2: Объектив с меньшей хроматической аберрацией.

В оптике что аберрация — это свойство оптических систем, таких как линзы , которое приводит к тому, свет распространяется по некоторой области пространства, а не фокусируется в одной точке. Аберрации приводят к размытию или искажению изображения, формируемого объективом, причем характер искажения зависит от типа аберрации. Аберрацию можно определить как отклонение характеристик оптической системы от предсказаний параксиальной оптики . В системе формирования изображений это происходит, когда свет из одной точки объекта не сходится (или не расходится) в одну точку после прохождения через систему. Аберрации возникают не из-за недостатков оптических элементов, а потому, что простая параксиальная теория не является полностью точной моделью воздействия оптической системы на свет.

Оптическая система формирования изображения с аберрацией создает нерезкое изображение. Производителям оптических инструментов необходимо корректировать оптические системы, чтобы компенсировать аберрации.

Аберрации можно проанализировать с помощью методов геометрической оптики . В статьях об отражении , преломлении и каустике обсуждаются общие особенности отраженных и преломленных лучей .

Обзор

Отражение от сферического зеркала. Лучи, падающие (красные) в сторону от центра зеркала, создают отраженные лучи (зеленые), которые не попадают в фокус F. Это происходит из-за сферической аберрации .

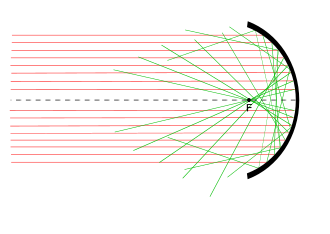
В идеальной линзе свет из любой точки объекта пройдет через линзу и соберется в одной точке плоскости изображения (или, в более общем смысле, поверхности изображения ). Однако настоящие линзы не фокусируют свет точно в одной точке, даже если они изготовлены идеально. Эти отклонения от идеализированных характеристик линзы называются аберрациями линзы.

Аберрации делятся на два класса: монохроматические и хроматические . Монохроматические аберрации вызваны геометрией линзы или зеркала и возникают как при отражении света, так и при его преломлении. Они появляются даже при использовании монохроматического света , отсюда и название.

Хроматические аберрации вызваны дисперсией линзы — изменением показателя преломления в зависимости от длины волны . Из-за дисперсии световые волны разной длины фокусируются в разных точках. Хроматическая аберрация не проявляется при использовании монохроматического света.

Монохроматические аберрации

Наиболее распространенными монохроматическими аберрациями являются:

• Расфокусировка
• Сферическая аберрация
• Есть
• Астигматизм
• Кривизна поля
• Искажение изображения

Хотя дефокусировка технически является оптической аберрацией низшего порядка, ее обычно не считают аберрацией объектива, поскольку ее можно исправить, перемещая линзу (или плоскость изображения), чтобы привести плоскость изображения в оптический фокус объектива. .

В дополнение к этим аберрациям, поршень и наклон являются эффектами, которые смещают положение фокусной точки. Поршень и наклон не являются настоящими оптическими аберрациями, поскольку, когда идеальный волновой фронт изменяется поршнем и наклоном, он все равно будет формировать идеальное изображение без аберраций, только сдвинутое в другое положение.

Хроматические аберрации

Сравнение идеального изображения кольца (1) и изображений только с осевой (2) и только поперечной (3) хроматической аберрацией

Основная статья: Хроматическая аберрация

Хроматическая аберрация возникает, когда волны разной длины не фокусируются в одной и той же точке. Типы хроматических аберраций:

• Осевая (или «продольная») хроматическая аберрация.
• Боковая (или «поперечная») хроматическая аберрация

Теория монохроматической аберрации

См. также: Объектив (оптика)

В идеальной оптической системе в теории оптики классической лучи света, исходящие из какой-либо точки объекта, объединяются в точку изображения ; и поэтому пространство объекта воспроизводится в пространстве изображений. Введение простых вспомогательных членов Гауссу по названные фокусными расстояниями и фокальными плоскостями , позволяют определить изображение любого объекта для любой системы. Однако теория Гаусса верна лишь до тех пор, пока углы, образуемые всеми лучами с оптической осью (симметричной осью системы), бесконечно малы, т. е. с бесконечно малыми объектами, изображениями и линзами; на практике эти условия могут не реализоваться, и изображения, проецируемые неисправленными системами, как правило, нечеткие и часто размытые, если апертура или поле зрения превышают определенные пределы.

Расследования Джеймса Клерка Максвелла и Эрнст Аббе показал, что свойства этих воспроизведений, т. е. относительное положение и величина изображений, являются не особыми свойствами оптических систем, а необходимыми следствиями предположения (по Аббе) о воспроизведении всех точек пространства в точках изображения, и независимы от способа, которым осуществляется воспроизведение. Эти авторы показали, однако, что ни одна оптическая система не может оправдать эти предположения, поскольку они противоречат фундаментальным законам отражения и преломления. Следовательно, теория Гаусса предоставляет лишь удобный метод приближения реальности; реалистичные оптические системы не соответствуют этому недостижимому идеалу. В настоящее время все, что можно сделать, — это проецировать одну плоскость на другую плоскость; но даже в этом случае всегда возникают отклонения, и маловероятно, что они когда-либо будут полностью исправлены.

Аберрация осевых точек (сферическая аберрация в узком смысле)

Рисунок 1

Пусть S (рис. 1) — любая оптическая система, лучи, исходящие из точки оси О под углом и1, объединятся в точке оси О'1; и те, что под углом и2 в точке оси О'2. Если есть преломление на коллективной сферической поверхности или через тонкую положительную линзу, O'2 будет лежать перед O'1 до тех пор, пока угол u2 больше, чем u1 ( при коррекции ); и наоборот, с дисперсионной поверхностью или линзами ( чрезмерная коррекция ). Каустика в первом случае напоминает знак > (больше); во втором < (меньше чем). Если угол u1 очень мал, O'1 — гауссово изображение; O'1 O'2 называется продольной аберрацией, а O'1R - аберрацией карандашей боковой с апертурой u2. Если карандаш с углом и2 представляет собой угол максимальной аберрации из всех переданных карандашей, то в плоскости, перпендикулярной оси О'1, имеется круговой диск нерезкости радиуса О'1R, а в параллельной плоскости при O'2 еще один радиусом O'2R2; между этими двумя находится диск наименьшего замешательства.

Наибольшее отверстие карандашей, принимающих участие в воспроизведении О, т. е. угол и, обычно определяется краем одной из линз или отверстием в тонкой пластинке, расположенной между линзами, перед ними или позади них. системы. Это отверстие называется упором или диафрагмой ; Аббе использовал термин диафрагма как для отверстия , так и для ограничивающего края линзы. Компонент S1 системы, расположенный между диафрагмой и объектом О, проецирует изображение диафрагмы, названное Аббе входным зрачком ; выходной зрачок — это изображение, формируемое компонентом S2, который расположен за диафрагмой. Все лучи, исходящие из О и проходящие через диафрагму, проходят также через входной и выходной зрачки, так как они являются изображениями диафрагменной диафрагмы. Поскольку максимальная апертура карандашей, выходящих из точки О, равна углу u, образуемому входным зрачком в этой точке, величина аберрации будет определяться положением и диаметром входного зрачка. Если система находиться целиком за диафрагменной диафрагмой, то это сам входной зрачок ( передний упор ); если полностью впереди, то это выходной зрачок ( задний упор ).

Если точка объекта бесконечно удалена, все лучи, полученные первым членом системы, параллельны, а их пересечения после прохождения системы изменяются в зависимости от высоты падения их перпендикуляра, т. е. их расстояния от оси. Это расстояние заменяет угол u в предыдущих соображениях; а апертура, т. е. радиус входного зрачка, является его максимальным значением.

Аберрация элементов, т.е. мельчайшие объекты, расположенные под прямым углом к ​​оси.

Если лучи, исходящие из точки О (рис. 1), совпадают, то из этого не следует, что точки на участке плоскости, перпендикулярном точке О оси, также будут совпадать, даже если эта часть плоскости очень мала. При увеличении диаметра линзы (т. е. при увеличении апертуры) соседняя точка N будет воспроизводиться, но сопровождаться аберрациями, сравнимыми по величине с ON. Этих аберраций можно избежать, если, согласно Аббе, условие синуса sin u'1/sin u1=sin u'2/sin u2 выполняется для всех лучей, воспроизводящих точку O. Если точка объекта O бесконечно удалена, u1 и u2 следует заменить на h1 и h2 — высоты падения перпендикуляров; тогда синусоидальное состояние становится sin u'1/h1=sin u'2/h2. Система, удовлетворяющая этому условию и свободная от сферических аберраций, называется апланатической (греч. а-, привативный, план, блуждающий). Это слово впервые было использовано Робертом Блэром для характеристики высшего ахроматизма, а впоследствии многими авторами также для обозначения свободы от сферической аберрации.

Поскольку аберрация увеличивается с удалением луча от центра линзы, аберрация увеличивается с увеличением диаметра линзы (или, соответственно, диаметра апертуры), а значит, может быть минимизирована за счет уменьшения апертуры, при стоимость также уменьшения количества света, попадающего в плоскость изображения.

Аберрация боковых точек объекта (точек за осью) узкими карандашами — астигматизм

Основная статья: Астигматизм (оптические системы)

Чтобы узнать об астигматизме глаза, см. Астигматизм .

Рисунок 2

Точка О (рис. 2) на конечном расстоянии от оси (или при бесконечно удаленном предмете — точка, образующая конечный угол при системе) вообще даже тогда не воспроизводится резко, если пучок лучей, испускающий от него и траверсную систему делают бесконечно узкими за счет уменьшения диафрагменного диафрагмы; такой карандаш состоит из лучей, которые могут пройти от точки предмета через теперь уже бесконечно малый входной зрачок. Видно (без учета исключительных случаев), что карандаш встречается с преломляющей или отражающей поверхностью не под прямым углом; поэтому он астигматичен (греч. а-, приватив, стигмия, точка). Назвав центральный луч, проходящий через входной зрачок, осью карандаша или главным лучом, можно сказать: лучи карандаша пересекаются не в одной точке, а в двух фокальных линиях, которые можно считать расположенными под прямым углом. к главному лучу; из них один лежит в плоскости, содержащей главный луч и ось системы, т. е. в первом главном сечении или меридиональном сечении , а другой - под прямым углом к ​​нему, т.е. во втором главном сечении или сагиттальном сечении. Мы получаем, следовательно, ни в одной перехватывающей плоскости за системой, как, например, фокусировочный экран, изображение точки объекта; с другой стороны, в каждой из двух плоскостей отдельно образуются линии О' и О" (в соседних плоскостях образуются эллипсы), а в плоскости между О' и О" - круг наименьшего нерезкости. Интервал О'О", называемый астигматической разницей, обычно увеличивается с увеличением угла W, образуемого главным лучом OP с осью системы, т. е. с полем зрения. Две поверхности астигматического изображения соответствуют одной плоскости объекта . ; и они соприкасаются в точке оси; на одной лежат фокальные линии первого рода, на другой - второго. Системы, в которых две астигматические поверхности совпадают, называются анастигматическими или стигматическими.

Сэр Исаак Ньютон, вероятно, был первооткрывателем астигмы; положение линий астигматического изображения определял Томас Янг; и теория была разработана Аллваром Галлстрандом . Библиография П. Кульмана приведена в книге Морица фон Рора «Генерация изображений в оптических приборах» .

Аберрация боковых точек объекта широкими карандашами — кома

При более широком открытии упора для боковых точек возникают такие же отклонения, как уже обсуждалось для осевых точек; но в данном случае они гораздо сложнее. Ход лучей в меридиональном сечении уже не симметричен главному лучу карандаша; и на пересекающей плоскости вместо светящейся точки появляется пятно света, не симметричное относительно точки и часто имеющее сходство с кометой, хвост которой направлен к оси или от нее. Из-за этого внешнего вида он получил свое название. Несимметричная форма меридионального карандаша — ранее единственного рассматриваемого — является комой только в более узком смысле; другие ошибки комы лечили Артур Кёниг и Мориц фон Рор. а затем Аллваром Галлстрандом.

Кривизна поля изображения

Основная статья: Кривизна поля Петцваля

Если устранить указанные выше ошибки, объединить две астигматические поверхности и получить резкое изображение при широкой апертуре, то остается необходимость корректировать кривизну поверхности изображения, особенно когда изображение приходится получать на плоской поверхности, например в фотографии. В большинстве случаев поверхность вогнута в сторону системы.

Искажение изображения

Рис. 3а: Бочкообразное искажение

Рис. 3b: Подушкообразное искажение

Даже если изображение резкое, оно может быть искажено по сравнению с идеальной проекцией через точечное отверстие . При точечной проекции увеличение объекта обратно пропорционально его расстоянию до камеры вдоль оптической оси, так что камера, направленная прямо на плоскую поверхность, воспроизводит эту плоскую поверхность. Искажение можно рассматривать как неравномерное растяжение изображения или, что то же самое, как изменение увеличения по полю. Хотя «искажение» может включать в себя произвольную деформацию изображения, наиболее выраженным видом искажения, создаваемым обычной оптикой формирования изображения, является «бочкообразное искажение», при котором центр изображения увеличивается больше, чем периметр (рисунок 3а). Обратный вариант, при котором периметр увеличивается больше, чем центр, известен как «подушкообразное искажение» (рис. 3б). Этот эффект называется искажением объектива или искажением изображения , и существуют алгоритмы для его исправления.

Системы, свободные от искажений, называются ортоскопическими (ортос, правый, скопеин смотреть) или прямолинейными (прямые).

Рисунок 4

Эта аберрация совершенно отлична от аберрации резкости воспроизведения; при нерезком воспроизведении возникает вопрос об искажении, если на рисунке можно распознать только части предмета. Если в нерезком изображении пятно света соответствует точке объекта, центр тяжести пятна можно рассматривать как точку изображения, то есть точку, в которой плоскость, принимающая изображение, например, фокусировочный экран, пересекает луч, проходящий через середину остановки. Это предположение оправдано, если плохое изображение на фокусировочном экране остается неподвижным при уменьшении диафрагмы; на практике это обычно происходит. Этот луч, названный Аббе главным лучом (не путать с главными лучами теории Гаусса), проходит через центр входного зрачка перед первым преломлением и центр выходного зрачка после последнего преломления. Отсюда следует, что правильность рисунка зависит исключительно от главных лучей; и не зависит от резкости или кривизны поля изображения. Ссылаясь на рис. 4, имеем O'Q'/OQ = a' tan w'/a tan w = 1/N, где N — масштаб или увеличение изображения. Чтобы N было постоянным для всех значений w, a' tan w'/a tan w также должно быть постоянным. Если отношение a'/a достаточно постоянно, как это часто бывает, приведенное выше соотношение сводится к условию Эйри , т.е. tan w'/ tan w= константа. Это простое соотношение (см. Camb. Phil. Trans., 1830, 3, стр. 1) выполняется во всех системах, симметричных относительно своей диафрагмы (кратко называемых симметричными или голосимметричными объективами ), или состоящих из двух одинаковых, но разнокалиберные компоненты, вынесенные из диафрагмы в соотношении их размеров и представляющие ей одинаковую кривизну (полусимметричные объективы); в этих системах tan w'/tan w = 1.

На постоянство a'/a, необходимое для поддержания этого соотношения, указывали Р. Х. Боу (Brit. Journ. Photog., 1861) и Томас Саттон (Photographic Notes, 1862); его лечили О. Люммер и М. фон Рор (Zeit. f. Instrumentenk., 1897, 17 и 1898, 18, стр. 4). Для этого необходимо, чтобы середина диафрагменной диафрагмы воспроизводилась в центрах входного и выходного зрачков без сферических аберраций. М. фон Рор показал, что для систем, не удовлетворяющих ни условию Эйри, ни условию Боу-Саттона, отношение a' cos w'/a tan w будет постоянным на одном расстоянии от объекта. Этому комбинированному условию в точности удовлетворяют голосимметричные объективы, воспроизводящие с масштабом 1, и полусимметричные, если масштаб воспроизведения равен отношению размеров двух компонентов.

Модель аберраций Цернике

Плоскость изображения балки с плоской вершиной под действием первых 21 полинома Цернике.

Эффект аберраций Цернике в логарифмическом масштабе. Видны минимумы интенсивности.

Круговые профили волнового фронта, связанные с аберрациями, можно математически смоделировать с использованием полиномов Цернике . Полиномы Цернике, разработанные Фрицем Цернике в 1930-х годах, ортогональны по окружности единичного радиуса. Сложный профиль аберрированного волнового фронта может быть аппроксимирован полиномами Цернике, чтобы получить набор коэффициентов аппроксимации , которые индивидуально представляют различные типы аберраций. Эти коэффициенты Цернике линейно независимы , поэтому отдельные вклады аберраций в общий волновой фронт могут быть изолированы и количественно оценены отдельно.

бывают четные и нечетные Полиномы Цернике . Четные полиномы Цернике определяются как

$Z_{n}^{m}(\rho ,\phi )=R_{n}^{m}(\rho )\,\cos(m\,\phi )\!$

и нечетные полиномы Цернике как

$Z_{n}^{-m}(\rho ,\phi )=R_{n}^{m}(\rho )\,\sin(m\,\phi ),\!$

где m и n — целые неотрицательные числа с $n\geq m$, Φ — азимутальный угол в радианах , а ρ — нормированное радиальное расстояние. Радиальные полиномы $R_{n}^{m}$ не имеют азимутальной зависимости и определяются как

$R_{n}^{m}(\rho )=\!\sum _{k=0}^{(n-m)/2}\!\!\!{\frac {(-1)^{k}\,(n-k)!}{k!\,((n+m)/2-k)!\,((n-m)/2-k)!}}\;\rho ^{n-2\,k}\quad {\mbox{if }}n-m{\mbox{ is even}}$

и $R_{n}^{m}(\rho )=0$ если $n-m$ странно.

Первые несколько полиномов Цернике, умноженные на соответствующие коэффициенты аппроксимации, составляют:

$a_{0}\times 1$	«Поршень», равный среднему значению волнового фронта.
$a_{1}\times \rho \cos(\phi )$	«X-Tilt», отклонение общего луча в сагиттальном направлении
$a_{2}\times \rho \sin(\phi )$	«Y-Tilt», отклонение габаритного луча в тангенциальном направлении.
$a_{3}\times (2\rho ^{2}-1)$	«Расфокусировка», параболический волновой фронт, возникающий из-за того, что он не в фокусе.
$a_{4}\times \rho ^{2}\cos(2\phi )$	«Астигматизм 0°», цилиндрическая форма по оси X или Y.
$a_{5}\times \rho ^{2}\sin(2\phi )$	«Астигматизм 45 °», цилиндрическая форма, ориентированная под углом ± 45 ° от оси X.
$a_{6}\times (3\rho ^{2}-2)\rho \cos(\phi )$	«X-Coma», комическое изображение, пылающее в горизонтальном направлении.
$a_{7}\times (3\rho ^{2}-2)\rho \sin(\phi )$	«Y-Кома», комическое изображение, пылающее в вертикальном направлении.
$a_{8}\times (6\rho ^{4}-6\rho ^{2}+1)$	«Сферическая аберрация третьего порядка».

где $\rho$ - нормированный радиус зрачка с $0\leq \rho \leq 1$, $\phi$ - азимутальный угол вокруг зрачка с $0\leq \phi \leq 2\pi$, а подгоночные коэффициенты $a_{0},\ldots ,a_{8}$ – ошибки волнового фронта в длинах волн.

Как и в Фурье синтезе с использованием синусов и косинусов , волновой фронт может быть идеально представлен достаточно большим количеством полиномов Цернике более высокого порядка. Однако волновые фронты с очень крутыми градиентами или очень высокой пространственной структурой частот , например, возникающие в результате распространения через атмосферную турбулентность или аэродинамические поля потока , плохо моделируются полиномами Цернике, которые имеют тенденцию фильтровать низкие частоты для точного пространственного определения волнового фронта. В этом случае другие методы подбора, такие как фракталы или разложение по сингулярным значениям, могут дать улучшенные результаты подбора.

Полиномы окружности были введены Фрицем Цернике для оценки точечного изображения аберрированной оптической системы с учетом эффектов дифракции . Идеальное изображение точки при наличии дифракции было описано еще Эйри еще в 1835 году. Потребовалось почти сто лет, чтобы прийти к всеобъемлющей теории и моделированию точечного изображения аберрированных систем (Цернике и Нейбоер). Анализ Нейбоера и Цернике описывает распределение интенсивности, близкое к оптимальной фокальной плоскости. Недавно была разработана расширенная теория, позволяющая рассчитывать амплитуду и интенсивность точечного изображения в гораздо большем объеме в фокальной области ( расширенная теория Нейбура-Цернике ). Эта расширенная теория формирования точечного изображения Нейбура-Цернике или «функция рассеяния точки» нашла применение в общих исследованиях формирования изображения, особенно для систем с высокой числовой апертурой , а также для характеристики оптических систем с точки зрения их аберраций.

Аналитическая обработка аберраций

Предыдущий обзор некоторых ошибок воспроизведения принадлежит теории аберраций Аббе, в которой определенные аберрации обсуждаются отдельно; он хорошо подходит для практических нужд, так как при построении оптического прибора стремятся устранить некоторые погрешности, выбор которых оправдан опытом. Однако в математическом смысле этот выбор произволен; воспроизведение конечного объекта с конечной апертурой влечет за собой, по всей вероятности, бесконечное число аберраций. Это число конечно только в том случае, если объект и апертура предполагаются бесконечно малыми определенного порядка ; и с каждым порядком бесконечной малости, т. е. с каждой степенью приближения к действительности (к конечным объектам и отверстиям), связано определенное количество аберраций. Эту связь обеспечивают только теории, которые рассматривают аберрации вообще и аналитически посредством неопределенных рядов.

Рисунок 5

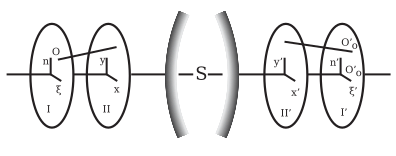
Луч, исходящий из точки объекта О (рис. 5), можно определить координатами (ξ, η). Из этой точки О в предметной плоскости I, перпендикулярной оси, и две другие координаты (x, y), точка, в которой луч пересекает входной зрачок, т. е. плоскость II. Аналогично соответствующий луч изображения может быть определен точками (ξ', η') и (x', y') в плоскостях I' и II'. Начало этих четырех плоских систем координат может быть коллинеарно оси оптической системы; и соответствующие оси могут быть параллельны. Каждая из четырех координат ξ', η', x', y' является функцией ξ, η, x, y; а если предположить, что поле зрения и апертура бесконечно малы, то ξ, η, x, y будут одного и того же порядка бесконечно малых; следовательно, разложив ξ', η', x', y' по возрастающим степеням ξ, η, x, y, получаются ряды, в которых необходимо учитывать только низшие степени. Легко видеть, что если оптическая система симметрична, начала систем координат коллинеарны с оптической осью и соответствующие оси параллельны, то при изменении знаков ξ, η, x, y значения ξ', η' , x', y' также должны изменить свой знак, но сохранить свои арифметические значения; это означает, что ряд ограничен нечетными степенями неотмеченных переменных.

Характер воспроизведения состоит в том, что лучи, исходящие из точки О, соединяются в другой точке О'; вообще говоря, это не так, поскольку ξ', η' меняются, если ξ, η постоянны, а x, y – переменны. Можно предположить, что плоскости I' и II' нарисованы там, где изображения плоскостей I и II образованы лучами вблизи оси по обычным правилам Гаусса; и путем расширения этих правил, однако не соответствующего действительности, можно было построить гауссово изображение точки О'0 _с координатами ξ'0 _, η'0 _. точки О, находящейся на некотором расстоянии от оси Записывая Dξ'=ξ'-ξ' ₀ и Dη'=η'-η' ₀ , тогда Dξ' и Dη' представляют собой аберрации, принадлежащие ξ, η и x, y, и являются функциями этих величин, которые при разложении последовательно содержат только нечетные степени по тем же причинам, что и указанные выше. За счет аберраций всех лучей, проходящих через О, в плоскости I' образуется пятно света, размер которого зависит от низших степеней ξ, η, x, y, содержащихся в аберрациях. Эти степени, названные Й. Петцваль числовые порядки изображения, следовательно, представляют собой только нечетные степени; условие образования образа т-го порядка состоит в том, что в рядах по Dξ' и Dη' коэффициенты при степенях 3-й, 5-й...(т-2)-й степени должны обращаться в нуль. Поскольку образы теории Гаусса третьего порядка, следующая задача — получить образ 5-го порядка, либо сделать коэффициенты при степенях 3-й степени нулевыми. Это требует выполнения пяти уравнений; другими словами, имеется пять изменений 3-го порядка, исчезновение которых дает изображение 5-го порядка.

Выражение этих коэффициентов через константы оптической системы, т. е. радиусы, толщины, показатели преломления и расстояния между линзами, было решено Л. Зейделем ; в 1840 г. Я. Петцваль построил свой портретный объектив на основе аналогичных расчетов, которые никогда не публиковались. Теорию разработал С. Финтерсвальдер, который также опубликовал посмертную статью Зейделя, содержащую краткий обзор его работ; более простую форму дал А. Кербер. А. Кениг и М. фон Рор представили метод Кербера, вывели формулы Зейделя из геометрических соображений, основанных на методе Аббе, и геометрически интерпретировали аналитические результаты.

Аберрации могут быть также выражены через характеристическую функцию системы и ее дифференциальные коэффициенты, а не через радиусы и т. д. линз; эти формулы не применимы непосредственно, но дают, однако, связь между числом аберраций и их порядком. Сэр Уильям Роуэн Гамильтон (British Assoc. Report, 1833, стр. 360) таким образом вывел аберрации третьего порядка; а в более позднее время метод продолжили Клерк Максвелл ( Proc. London Math. Soc., 1874–1875; (см. также трактаты Р. С. Хита и Л. А. Германа), М. Тизен ( Berlin. Akad. Sitzber., 1890, 35, с. 804), Г. Брунса ( Leipzig. Math. Phys. Ber., 1895, 21, с. 410), и особенно успешно К. Шварцшильда ( Göttingen. Akad. Abhandl., 1905, 4, No. 1), открывший таким образом аберрации 5-го порядка (их девять) и, возможно, самое краткое доказательство практических (Зейделя) формул А. Гулстранда (см. выше и Ann. d. Phys., 1905, 18, с. 941) основал свою теорию аберраций на дифференциальной геометрии поверхностей.

Аберрациями третьего порядка являются: 1) аберрация точки оси; (2) аберрации точек, расстояние от оси которых очень мало, менее третьего порядка — отклонение от синусоидального состояния и кома здесь попадают в один класс; (3) астигматизм; (4) кривизна поля; (5) искажение.

1. Аберрации осевых точек третьего порядка рассматриваются во всех учебниках по оптике. Это очень важно при проектировании телескопа. В телескопах за апертуру обычно принимают линейный диаметр объектива. Это не то же самое, что апертура микроскопа, которая основана на входном зрачке или поле зрения, видимом со стороны объекта, и выражается как угловое измерение. Аберрациями более высокого порядка в конструкции телескопа можно в основном пренебречь. Для микроскопов этим нельзя пренебрегать. Для одиночной линзы очень малой толщины и заданной силы аберрация зависит от отношения радиусов r:r' и является минимальной (но никогда не нулевой) для определенного значения этого отношения; он изменяется обратно пропорционально показателю преломления (сила линзы остается постоянной). Суммарная аберрация двух или более соприкасающихся очень тонких линз, будучи суммой отдельных аберраций, может равняться нулю. Это также возможно, если линзы имеют одинаковый алгебраический знак. Из тонких положительных линз с n=1,5 для коррекции сферической аберрации третьего порядка необходимы четыре. Однако эти системы не имеют большого практического значения. В большинстве случаев комбинируются две тонкие линзы, одна из которых имеет именно такую ​​сильную положительную аберрацию ( недостаточная коррекция, см. выше), в то время как другое является отрицательным; первая должна быть положительной линзой, а вторая – отрицательной; однако силы могут различаться, поэтому желаемый эффект линзы сохраняется. Обычно преимуществом является обеспечение большого преломляющего эффекта с помощью нескольких более слабых линз, чем одной мощной линзы. Одной, а также несколькими и даже бесконечным числом тонких линз, соприкасающихся, можно воспроизвести без аберрации третьего порядка не более двух осевых точек. Свобода от аберрации для двух точек оси, одна из которых бесконечно удалена, известна как условие Гершеля. Все эти правила действительны, поскольку не учитываются толщина и расстояние между линзами.
2. Условие свободы от комы третьего порядка важно и для объективов телескопов; это известно как состояние Фраунгофера . (4) После устранения аберрации На оси, комы и астигматизма соотношение неплоскостности поля в третьем порядке выражается уравнением Петцваля S1/r(n'−n) = 0, где r — радиус преломляющей поверхности, n и n' — показатели преломления соседних сред, S — знак суммы всех преломляющих поверхностей.

Практическое устранение аберраций

Лазерные направляющие звезды помогают устранить атмосферные искажения.

Классическая задача визуализации состоит в том, чтобы идеально воспроизвести конечную плоскость (объект) на другой плоскости (изображение) через конечную апертуру. Невозможно сделать это идеально для более чем одной такой пары плоскостей (это было доказано с возрастающей общностью Максвеллом в 1858 году, Брунсом в 1895 году и Каратеодори в 1926 году, см. резюме в Walther, A., J. Opt. Соц. А 6 , 415–422 (1989)). Однако для одной пары плоскостей (например, для одной фокусировки объектива) проблема в принципе может быть решена идеально. Примерами такой теоретически совершенной системы являются линза Люнебурга и «рыбий глаз» Максвелла .

Практические методы решают эту задачу с точностью, большей частью достаточной для специального назначения каждого вида приборов. Задачу о нахождении системы, воспроизводящей данный объект на данной плоскости с заданным увеличением (с учетом аберраций), можно было бы решить с помощью теории приближения; однако в большинстве случаев аналитические трудности были слишком велики для старых методов расчета, но их можно улучшить за счет применения современных компьютерных систем. Однако решения были получены в частных случаях. В настоящее время конструкторы почти всегда пользуются обратным методом: составляют систему на основе определенных, часто весьма личных опытов, и проверяют тригонометрическим расчетом путей нескольких лучей, дает ли система желаемое воспроизведение (примеры приведены в А. Глейхен, Lehrbuch der geometrischen Optik , Лейпциг и Берлин, 1902). Радиусы, толщины и расстояния постоянно изменяются до тех пор, пока ошибки изображения не станут достаточно малыми. Этим методом исследуются лишь отдельные ошибки воспроизводства, особенно отдельные члены или все из названных выше. Теория аналитической аппроксимации часто применяется временно, поскольку ее точности обычно недостаточно.

Чтобы сделать сферическую аберрацию и отклонение от синусоидального условия малыми во всей апертуре, лучу с конечным углом апертуры и* (шириной бесконечно удаленных предметов: с конечной высотой падения h*) придается то же самое расстояние пересечения и такое же отношение синуса, как и у соседнего с осью (u* или h* не может быть намного меньше, чем наибольшая апертура U или H, которая будет использоваться в системе). Лучи с углом раскрытия меньшим, чем u*, не будут иметь одинаковое расстояние пересечения и одинаковое соотношение синусов; эти отклонения называются зонами, и конструктор стремится свести их к минимуму. То же справедливо и для ошибок, зависящих от угла поля зрения w: астигматизм, кривизна поля и дисторсия устраняются при определенном значении w*, зоны астигматизма, кривизна поля и дисторсия - при меньших значениях w. . Практик-оптик называет такие системы: с поправкой на угол апертуры и* (высота падения h*) или на угол поля зрения w*. Сферические аберрации и изменения синусоидальных отношений часто представляются графически как функции апертуры, точно так же, как отклонения двух астигматических поверхностей изображения от плоскости изображения точки оси представляются как функции углов поля зрения. .

Следовательно, окончательная форма практической системы основывается на компромиссе; Увеличение апертуры приводит к уменьшению доступного поля зрения, и наоборот. Но большая апертура даст большее разрешение. Типичными можно считать следующее:

1. Самая большая апертура; необходимые поправки — для точки оси и синусоидального состояния; ошибки поля зрения практически не учитываются; пример — мощные объективы микроскопа.
2. Широкоугольный объектив ; необходимые поправки — на астигматизм, кривизну поля и дисторсию; ошибки апертуры учитываются незначительно; примеры — фотографические широкоугольные объективы и окуляры.
   Между этими крайними примерами стоит обычный объектив : он больше корректируется в отношении диафрагмы; цели для групп больше связаны с полем зрения.
3. Длиннофокусные объективы имеют маленькое поле зрения, и аберрации по оси очень важны. Поэтому зоны должны быть как можно меньшими, а дизайн должен подчеркивать простоту. По этой причине эти линзы лучше всего подходят для аналитических вычислений.

Хроматическая или цветовая аберрация

В оптических системах, состоящих из линз, положение, величина и ошибки изображения зависят от показателей преломления используемого стекла (см. « Линза (оптика) и монохроматическая аберрация » выше). Так как показатель преломления меняется в зависимости от цвета или длины волны света (см. Дисперсия ), то отсюда следует, что система линз (нескорректированных) проецирует изображения разных цветов в несколько разных местах и ​​размерах и с разными аберрациями; т.е. существуют хроматические различия расстояний пересечения, увеличений и монохроматических аберраций. Если используется смешанный свет (например, белый свет), все эти изображения формируются и вызывают путаницу, называемую хроматической аберрацией; например, вместо белого поля на темном фоне воспринимается цветное поле или узкий спектр. Отсутствие этой ошибки называется ахроматизмом, а исправленная таким образом оптическая система называется ахроматической. Говорят, что система хроматически недостаточно исправлена, если она демонстрирует хроматическую ошибку того же типа, что и тонкая положительная линза, в противном случае говорят, что она перекорректировано.

Если, во-первых, пренебречь монохроматическими аберрациями (другими словами, принять теорию Гаусса), то всякое воспроизведение будет определяться положением фокальных плоскостей и величиной фокусных расстояний, или если фокусные расстояния, как обычно бывает равным трем константам воспроизводства. Эти константы определяются данными системы (радиусами, толщинами, расстояниями, индексами и т. д. линз); поэтому их зависимость от показателя преломления, а следовательно и от цвета, являются расчетными. Показатели преломления для разных длин волн должны быть известны для каждого типа используемого стекла. Таким образом соблюдаются условия, что любая константа воспроизведения одинакова для двух разных цветов, т. е. эта константа ахроматизирована. Например, можно одной толстой линзой в воздухе ахроматизировать положение фокальной плоскости на величину фокусного расстояния. Если все три константы воспроизведения ахроматизированы, то гауссово изображение для всех расстояний до объектов одинаково для двух цветов, и говорят, что система находится в устойчивом ахроматизме.

На практике выгоднее (по Аббе) определить хроматическую аберрацию (например, расстояние пересечения) для фиксированного положения объекта и выразить ее суммой, в которой каждый компонент содержит величину, причитающуюся каждому преломляющая поверхность. В плоскости, содержащей точку изображения одного цвета, другой цвет создает диск нерезкости; это похоже на путаницу, вызванную двумя зонами сферической аберрации. Для бесконечно удаленных объектов радиус хроматического диска нерезкости пропорционален линейной апертуре и не зависит от фокусного расстояния ( см. выше , Монохроматическая аберрация точки оси ); а так как этот диск становится менее вредным при увеличении изображения данного предмета или при увеличении фокусного расстояния, то отсюда следует, что ухудшение изображения пропорционально отношению апертуры к фокусному расстоянию, т. е. относительному апертуру. (Это объясняет гигантские фокусные расстояния, которые были в моде до открытия ахроматизма.)

Примеры:

1. В очень тонкой линзе на воздухе должна соблюдаться только одна константа воспроизведения, так как фокусное расстояние и расстояние до фокуса равны. Если показатель преломления одного цвета будет $n$и для другого $n+dn$, а степени или обратные величины фокусных расстояний будут $f$ и $f+df$, затем $${\dfrac {df}{f}}={\dfrac {dn}{(n-1)}}={\dfrac {1}{n}},$$ $dn$ называется дисперсией, а $n$ рассеивающая способность стекла.
2. Две тонкие линзы в контакте: пусть $f_{1}$ и $f_{2}$ – силы, соответствующие линзам с показателями преломления $n_{1}$ и $n_{2}$ и радиусы $r'_{1}$, $r''_{1}$, и $r'_{2}$, $r''_{2}$ соответственно; позволять $f$ обозначают полную мощность, а $df$, $dn_{1}$, $dn_{2}$ изменения $f$, $n_{1}$, и $n_{2}$ с цветом. Тогда имеют место следующие соотношения:
   • $f=f_{1}-f_{2}=(n_{1}-1)(1/r'_{1}-1/r''_{1})+(n2-1)(1/r'_{2}-1/r''_{2})=(n_{1}-1)k_{1}+(n_{2}-1)k_{2}$; и
   • $df=k_{1}dn_{1}+k_{2}dn_{2}$. Для ахроматизма $df=0$, следовательно, из (3)
   • $k_{1}/k_{2}=-dn_{2}/dn_{1}$, или $f_{1}/f_{2}=-n_{1}/n_{2}$. Поэтому $f_{1}$ и $f_{2}$ должны иметь разные алгебраические знаки, или система должна состоять из коллективной и дисперсионной линз. Следовательно, полномочия этих двух должны быть разными (для того, чтобы $f$ не равна нулю (уравнение 2)), и дисперсионные силы также должны быть разными (согласно 4).

Ньютон не смог осознать существование сред с различной дисперсионной способностью, требуемой ахроматизмом; следовательно, он построил большие отражатели вместо рефракторов. Джеймс Грегори и Леонард Эйлер пришли к правильному взгляду на основе ложного представления об ахроматизме глаза; это было установлено Честером Мором Холлом в 1728 году, Клингеншерной в 1754 году и Доллондом в 1757 году, которые сконструировали знаменитые ахроматические телескопы. (См. телескоп .)

Стекло с более слабой дисперсионной способностью (большая $v$) называют коронным стеклом ; что с большей дисперсионной способностью, бесцветное стекло . Для построения ахроматической коллективной линзы ( $f$ положительно) из уравнения (4) следует, что коллективная линза I. из крон-стекла и дисперсионная линза II. необходимо выбирать бесцветное стекло; последний, хотя и более слабый, хроматически корректирует другой за счет своей большей дисперсионной способности. Для ахроматической линзы с дисперсией необходимо принять обратное. В настоящее время это обычный тип объектива телескопа; значения четырех радиусов должны удовлетворять уравнениям (2) и (4). Можно также постулировать два других условия: первое — это всегда устранение аберрации на оси; второе — либо условие Гершеля , либо условие Фраунгофера, причем последнее является лучшим (см. выше « Монохроматическая аберрация» ). На практике, однако, часто бывает полезнее избежать второго условия, обеспечивая контакт линз, т.е. равные радиусы. По мнению П. Рудольфа (Eder's Jahrb. f. Photog., 1891, 5, с. 225; 1893, 7, с. 221), склеенные объективы тонких линз позволяют устранить сферическую аберрацию на оси, если, как указано выше, , коллективная линза имеет меньший показатель преломления; с другой стороны, они позволяют устранить астигматизм и кривизну поля, если коллективная линза имеет больший показатель преломления (это следует из уравнения Петцваля; см. Л. Зейдель, Astr. Nachr., 1856, стр. 289) . Если сцементированная система положительна, то и более мощная линза должна быть положительной; и, согласно (4), большей мощности принадлежит более слабая дисперсионная мощность (большая $v$), то есть коронное стекло; следовательно, коронное стекло должно иметь больший показатель преломления для астигматических и плоских изображений. Однако во всех более ранних видах стекла дисперсионная способность увеличивалась с увеличением показателя преломления; то есть, $v$ уменьшилось, как $n$ повысился; но некоторые из йенских стекол Э. Аббе и О. Шотта были крон-стеклами с высоким показателем преломления, а ахроматические системы из таких крон-стекл с кремневыми стеклами с меньшим показателем преломления называются новыми ахроматами и применялись П. Рудольф в первых анастигматах (фотообъективах).

Вместо того, чтобы делать $df$ исчезнуть, ему можно присвоить определенное значение, которое за счет сложения двух линз создаст любое желаемое хроматическое отклонение, например, достаточное для устранения отклонения, присутствующего в других частях системы. Если линзы I. и II. быть склеенным и иметь одинаковый показатель преломления для одного цвета, то его эффект для этого цвета будет таким же, как у цельной линзы; путем такого разложения линзы ее можно по желанию сделать хроматической или ахроматической, не изменяя ее сферического эффекта. Если его хроматический эффект ( $df/f$) больше, чем у той же линзы, поскольку она изготовлена ​​из более дисперсионного из двух используемых стекол, ее называют гиперхромной.

Для двух тонких линз, разделенных расстоянием $D$ условие ахроматизма $D=v_{1}f_{1}+v_{2}f_{2}$; если $v_{1}=v_{2}$ (например, если линзы изготовлены из одного и того же стекла), это сводится к $D=(f_{1}+f_{2})/2$, известное как состояние окуляров.

Если константу воспроизведения, например фокусное расстояние, сделать одинаковой для двух цветов, то она не будет одинаковой для других цветов, если использовать два разных стекла. Например, условие ахроматизма (4) для двух контактирующих тонких линз выполняется только в одной части спектра, поскольку $dn_{2}/dn_{1}$ варьируется в пределах спектра. Этот факт был впервые установлен И. Фраунгофером, определившим цвета посредством темных линий солнечного спектра; и показал, что соотношение дисперсии двух стекол варьируется примерно на 20% от красного до фиолетового (отклонение для стекла и воды составляет около 50%). Если, следовательно, для двух цветов, а и b, $f_{a}=f_{b}=f$, то для третьего цвета c фокусное расстояние будет другим; то есть, если c лежит между a и b, то $f_{c}<f$и наоборот; эти алгебраические результаты следуют из того факта, что в сторону красного цвета преобладает дисперсия положительного кронного стекла, а в сторону фиолетового — отрицательного кремня. Эти хроматические ошибки систем, которые являются ахроматическими для двух цветов, называются вторичным спектром и зависят от апертуры и фокусного расстояния так же, как и первичные хроматические ошибки.

На рис. М. фон Рора 6, взято из «Теории и истории фотографического объектива» , по оси абсцисс — фокусные расстояния, а по ординатам — длины волн. Используемые линии Фраунгофера показаны в соседней таблице.

А'	С	Д	Зеленая ртуть .	Ф	Г'	Фиолетовый ртуть.
767.7	656.3	589.3	546.1	486.2	454.1	405,1 нм

Рисунок 6

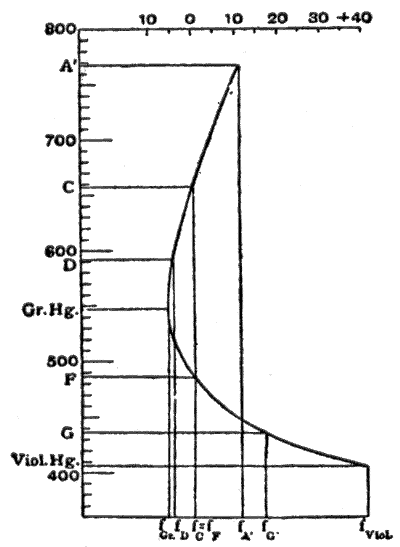
Фокусные расстояния для линий C и F выравниваются. В районе 550 нм касательная к кривой параллельна оси длин волн; а фокусное расстояние меняется меньше всего в достаточно большом диапазоне цветов, поэтому в этом соседстве цветовой союз на высоте. Более того, эта область спектра является той, которая кажется человеческому глазу наиболее яркой, и, следовательно, эта кривая вторичного спектра, полученная путем создания $f_{C}=f_{F}$, является, по данным опытов сэра Г. Г. Стокса (Proc. Roy. Soc., 1878), наиболее пригодным для зрительных приборов ( оптический ахроматизм, ). Аналогичным образом для систем, используемых в фотографии, вершина цветовой кривой должна располагаться в положении максимальной чувствительности пластинок; обычно предполагается, что это точка G'; и для этого линии F и фиолетовой ртути объединяются. Эта уловка специально применяется в объективах для астрономической фотографии ( чистый актинический ахроматизм ). Однако для обычной фотографии есть один недостаток: изображение на фокусировочном экране и правильная настройка фоточувствительной пластинки не совпадают; в астрономической фотографии эта разница постоянна, но в других видах она зависит от расстояния до объектов. По этой причине линии D и G' объединены для обычных фотографических объективов; оптическое, как и актиническое изображение, хроматически уступает, но оба лежат в одном и том же месте; и, следовательно, лучшая коррекция лежит в F (это известно как актиническая коррекция или освобождение от химического фокуса ).

Должны ли быть в двух контактирующих линзах одинаковые фокусные расстояния для трех цветов a, b и c, т.е. $f_{a}=f_{b}=f_{c}=f$, то относительная парциальная дисперсия $(n_{c}-n_{b})(n_{a}-n_{b})$ должно быть одинаковым для двух видов используемого стекла. Это следует из рассмотрения уравнения (4) для двух пар цветов ac и bc. До недавнего времени не было известно очков с пропорциональной степенью поглощения; но Р. Блэр (Trans. Edin. Soc., 1791, 3, стр. 3), П. Барлоу и Ф. С. Арчер преодолели эту трудность, построив жидкие линзы между стеклянными стенками. Фраунгофер приготовил очки, уменьшающие вторичный спектр; но постоянный успех был обеспечен только с появлением йенских очков Э. Аббе и О. Шоттом. При использовании очков, не имеющих пропорциональной дисперсии, отклонение третьего цвета можно устранить двумя линзами, если между ними допустить интервал; или тремя контактирующими линзами, которые не все могут состоять из старых очков. При соединении трех цветов ахроматизм более высокого порядка получается ; еще существует остаточный третичный спектр, но им всегда можно пренебречь.

Теория Гаусса является лишь приближением; все равно возникают монохроматические или сферические аберрации, которые для разных цветов будут разными; и если бы они были компенсированы одним цветом, изображение другого цвета оказалось бы тревожным. Наиболее важным является хроматическая разница аберрации точки оси, которая все еще присутствует и нарушает изображение после того, как параосевые лучи разных цветов объединены соответствующей комбинацией очков. Если коллективную систему скорректировать по оси оси для определенной длины волны, то из-за большей дисперсии отрицательных компонент — кремневых стекол — возникнет сверхкоррекция для более коротких длин волн (это ошибка отрицательных компонент). и недостаточная коррекция для более длинных волн (ошибка линз из кронового стекла преобладает в красном цвете). Эту ошибку рассмотрели Жан ле Рон д'Аламбер и особенно подробно К. Ф. Гаусс. Он быстро увеличивается с увеличением апертуры и более важен при средних апертурах, чем вторичный спектр параксиальных лучей; следовательно, сферическую аберрацию необходимо устранить для двух цветов, а если это невозможно, то ее следует устранить для тех конкретных длин волн, которые наиболее эффективны для рассматриваемого прибора (графическое изображение этой ошибки дано у М. фон Рора, Теория и история фотообъектива ).

Условие воспроизведения элемента поверхности в месте резко воспроизведенной точки — константа синусоидальной зависимости должно выполняться и при больших апертурах для нескольких цветов. Э. Аббе удалось вычислить объективы микроскопа, свободные от ошибки точки оси и удовлетворяющие условию синуса для нескольких цветов, которые поэтому, по его определению, были апланатическими для нескольких цветов ; такие системы он назвал апохроматическими . Хотя увеличение отдельных зон одинаково, оно не одинаково для красного и для синего; и есть хроматическая разница в увеличении. В таком же количестве, но в противоположном смысле, его производят окуляры, которые Аббе использовал с этими объективами ( компенсирующие окуляры ), так что он устраняется на изображении всего микроскопа. Лучшие объективы телескопов и фотографические объективы, предназначенные для трехцветной работы, также являются апохроматическими, даже если они не обладают таким же качеством коррекции, как объективы микроскопа. Хроматические различия других ошибок воспроизведения редко имеют практическое значение.

См. также

• Аберрации глаза
• Оптический телескоп § Пять аберраций Зейделя
• Кодирование волнового фронта

Внешние ссылки

• Цели микроскопа: раздел «Оптические аберрации» на веб-сайте «Молекулярные выражения» , Майкл В. Дэвидсон, Мортимер Абрамовиц, Olympus America Inc. и Университет штата Флорида.