Numerical method for differential equations
В численном анализе метод локальной линеаризации (ЛЛ) представляет собой общую стратегию разработки числовых интеграторов для дифференциальных уравнений, основанную на локальной (кусочной) линеаризации данного уравнения на последовательных интервалах времени. Затем числовые интеграторы итеративно определяются как решение полученного кусочно-линейного уравнения в конце каждого последовательного интервала. Метод ЛЛ был разработан для различных уравнений, таких как обыкновенные , запаздывающие , случайные и стохастические дифференциальные уравнения. Интеграторы LL являются ключевым компонентом в реализации методов вывода для оценки неизвестных параметров и ненаблюдаемых переменных дифференциальных уравнений с учетом временных рядов (потенциально зашумленных) наблюдений. Схемы LL идеально подходят для работы со сложными моделями в различных областях, таких как нейронаука , финансы , управление лесным хозяйством , техника управления , математическая статистика и т. д.
Предыстория [ править ] Дифференциальные уравнения стали важным математическим инструментом для описания эволюции во времени ряда явлений, например, вращения планет вокруг Солнца, динамики цен активов на рынке, пожара нейронов, распространения эпидемий и т. д. Однако поскольку точные решения этих уравнений обычно неизвестны, необходимы численные аппроксимации к ним, полученные с помощью численных интеграторов. В настоящее время многие приложения в инженерных и прикладных науках, ориентированные на динамические исследования, требуют разработки эффективных численных интеграторов, максимально сохраняющих динамику этих уравнений. С этой основной мотивацией были разработаны интеграторы локальной линеаризации.
линеаризации высокого порядка Метод локальной Метод локальной линеаризации высокого порядка (HOLL) устойчивость и динамику линейных уравнений. Интеграторы получаются путем разделения на последовательных интервалах времени решения x исходного уравнения на две части: решение z локально линеаризованного уравнения плюс аппроксимация невязки высокого порядка. r = x − z {\displaystyle \mathbf {r} =\mathbf {x} -\mathbf {z} }
Схема локальной линеаризации [ править ] Схема локальной линеаризации (LL) рекурсивный алгоритм , который позволяет численно реализовать дискретизацию , полученную на основе метода LL или HOLL, для класса дифференциальных уравнений.
Методы LL для ODE [ править ] Рассмотрим d -мерное обыкновенное дифференциальное уравнение (ОДУ)
d x ( t ) d t = f ( t , x ( t ) ) , t ∈ [ t 0 , T ] , ( 4.1 ) {\displaystyle {\frac {d\mathbf {x} \left(t\right)}{dt}}=\mathbf {f} \left(t,\mathbf {x} \left(t\right)\right),\qquad t\in \left[t_{0},T\right],\qquad \qquad \qquad \qquad (4.1)}
с начальным состоянием x ( t 0 ) = x 0 {\displaystyle \mathbf {x} (t_{0})=\mathbf {x} _{0}} f {\displaystyle \mathbf {f} }
Позволять ( t ) h = { t n : n = 0 , . . , N } {\displaystyle \left(t\right)_{h}=\{t_{n}:n=0,..,N\}} [ t 0 , T ] {\displaystyle [t_{0},T]} h таким, что t n < t n + 1 {\displaystyle t_{n}<t_{n+1}} h n = t n + 1 − t n ≤ h {\displaystyle h_{n}=t_{n+1}-t_{n}\leq h} t n {\displaystyle t_{n}} констант дает
x ( t n + h ) = x ( t n ) + ϕ ( t n , x ( t n ) ; h ) + r ( t n , x ( t n ) ; h ) , {\displaystyle \mathbf {x} (t_{n}+h)=\mathbf {x} (t_{n})+\mathbf {\phi } (t_{n},\mathbf {x} (t_{n});h)+\mathbf {r} (t_{n},\mathbf {x} (t_{n});h),}
где
ϕ ( t n , z n ; h ) = ∫ 0 h e f x ( t n , z n ) ( h − s ) ( f ( t n , z n ) + f t ( t n , z n ) s ) d s {\displaystyle \mathbf {\phi } (t_{n},\mathbf {z} _{n};h)=\int \limits _{0}^{h}e^{\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})(h-s)}(\mathbf {f} (t_{n},\mathbf {z} _{n})+\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})s)\,ds\qquad }
результат линейного приближения, и
r ( t n , z n ; h ) = ∫ 0 h e f x ( t n , z n ) ( h − s ) g n ( s , x ( t n + s ) ) d s , ( 4.2 ) {\displaystyle \mathbf {r} (t_{n},\mathbf {z} _{n};h)=\int \limits _{0}^{h}e^{\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})(h-s)}\mathbf {g} _{n}(s,\mathbf {x} (t_{n}+s))\,ds,\qquad \qquad \qquad (4.2)}
– остаток линейного приближения. Здесь, f x {\displaystyle \mathbf {f} _{\mathbf {x} }} f t {\displaystyle \mathbf {f} _{t}} f по переменным x и t соответственно, и g n ( s , u ) = f ( s , u ) − f x ( t n , z n ) u − f t ( t n , z n ) ( s − t n ) − f ( t n , z n ) + f x ( t n , z n ) z n . {\displaystyle \mathbf {g} _{n}(s,\mathbf {u} )=\mathbf {f} (s,\mathbf {u} )-\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})\mathbf {u} -\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})(s-t_{n})-\mathbf {f} (t_{n},\mathbf {z} _{n})+\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})\mathbf {z} _{n}.}
Локальная дискретизация линейная Для временной дискретизации ( t ) h {\displaystyle \left(t\right)_{h}} Локальная линейная дискретизация ОДУ (4.1) в каждой точке t n + 1 ∈ ( t ) h {\displaystyle t_{n+1}\in \left(t\right)_{h}} [1] [2]
z n + 1 = z n + ϕ ( t n , z n ; h n ) , with z 0 = x 0 . ( 4.3 ) {\displaystyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h_{n}),\qquad {\text{ with }}\quad \mathbf {z} _{0}=\mathbf {x} _{0}.\qquad \qquad \qquad \qquad (4.3)}
Локальная линейная дискретизация (4.3) сходится с порядком 2 [3]
высокого порядка дискретизация Локальная линейная Для временной дискретизации ( t ) h , {\displaystyle (t)_{h},} локальная линейная (ХОЛЛ) дискретизация ОДУ (4.1) высокого порядка в каждой t n + 1 ∈ ( t ) h {\displaystyle t_{n+1}\in (t)_{h}} [1] [4] [5] [6]
z n + 1 = z n + ϕ ( t n , z n ; h n ) + r ~ ( t n , z n ; h n ) , with z 0 = x 0 , ( 4.4 ) {\displaystyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h_{n})+{\widetilde {\mathbf {r} }}(t_{n},\mathbf {z} _{n};h_{n}),\qquad {\text{ with }}\quad \mathbf {z} _{0}=\mathbf {x} _{0},\qquad \qquad \qquad (4.4)}
где r ~ {\displaystyle {\tilde {r}}} α {\displaystyle \alpha } 2 ) аппроксимация невязки r ( i . e . , | r ( t n , z n ; h ) − r ~ ( t n , z n ; h ) | ∝ h α + 1 ) . {\displaystyle (i.e.,\left\vert \mathbf {r} (t_{n},\mathbf {z} _{n};h)-{\widetilde {\mathbf {r} }}(t_{n},\mathbf {z} _{n};h)\right\vert \propto h^{\alpha +1}).} сходится с порядком α {\displaystyle \alpha }
Дискретизация ХОЛЛА может быть получена двумя способами: [1] [4] [5] [6] r ; и 2) (на основе интегратора) с использованием числового интегратора для дифференциального представления r, определенного формулой
d r ( t ) d t = q ( t n , z n ; t , r ( t ) ) , with r ( t n ) = 0 , ( 4.5 ) {\displaystyle {\frac {d\mathbf {r} (t)}{dt}}=\mathbf {q} (t_{n},\mathbf {z} _{n};t\mathbf {,\mathbf {r} } (t)\mathbf {)} ,\qquad {\text{ with }}\qquad \mathbf {r} (t_{n})=\mathbf {0,} \qquad \qquad \qquad (4.5)}
для всех t ∈ [ t k , t k + 1 ] {\displaystyle t\in \lbrack t_{k},t_{k+1}]}
q ( t n , z n ; s , ξ ) = f ( s , z n + ϕ ( t n , z n ; s − t n ) + ξ ) − f x ( t n , z n ) ϕ ( t n , z n ; s − t n ) − f t ( t n , z n ) ( s − t n ) − f ( t n , z n ) . {\displaystyle \mathbf {q} (t_{n},\mathbf {z} _{n};s\mathbf {,\xi } )=\mathbf {f} (s,\mathbf {z} _{n}+\mathbf {\phi } \left(t_{n},\mathbf {z} _{n};s-t_{n}\right)+\mathbf {\xi } )-\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})\mathbf {\phi } (t_{n},\mathbf {z} _{n};s-t_{n})-\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})(s-t_{n})-\mathbf {f} (t_{n},\mathbf {z} _{n}).}
Локально линеаризованная дискретизация Рунге-Кутты [6] [4] z n + 1 = z n + ϕ ( t n , z n ; h n ) + h n ∑ j = 1 s b j k j , with k i = q ( t n , z n ; t n + c i h n , h n ∑ j = 1 i − 1 a i j k j ) , {\displaystyle \qquad \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h_{n})+h_{n}\sum _{j=1}^{s}b_{j}\mathbf {k} _{j},\quad {\text{ with }}\quad \mathbf {k} _{i}=\mathbf {q} (t_{n},\mathbf {z} _{n};{\text{ }}t_{n}+c_{i}h_{n}\mathbf {,} \mathbf {} h_{n}\sum _{j=1}^{i-1}a_{ij}\mathbf {k} _{j}),}
которое получается в результате решения (4.5) по s-этапной явной схеме Рунге–Кутты (РК) с коэффициентами c = [ c i ] , A = [ a i j ] a n d b = [ b j ] {\displaystyle \mathbf {c} =\left[c_{i}\right],\mathbf {A} =\left[a_{ij}\right]\quad and\quad \mathbf {b} =\left[b_{j}\right]}
Локальная линейная дискретизация Тейлора [5]
z n + 1 = z n + ϕ ( t n , z n ; h n ) + ∫ 0 h n e ( h n − s ) f x ( t n , z n ) ∑ j = 2 p c n , j j ! s j d s , with c n , j = ( d j + 1 x ( t ) d t j + 1 − f x ( t n , z n ) d j x ( t ) d t j ) ∣ t = z n , {\displaystyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h_{n})+\int _{0}^{h_{n}}e^{(h_{n}-s)\mathbf {f} _{\mathbf {x} }\left(t_{n},\mathbf {z} _{n}\right)}\sum _{j=2}^{p}{\frac {\mathbf {c} _{n,j}}{j!}}s^{j}\,ds,{\text{ with }}\mathbf {c} _{n,j}=\left({\frac {d^{j+1}\mathbf {x} (t)}{dt^{j+1}}}-\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n}){\frac {d^{j}\mathbf {x} (t)}{dt^{j}}}\right)\mid _{t=\mathbf {z} _{n}},}
что является результатом аппроксимации g n {\displaystyle \mathbf {g} _{n}} порядка p усеченным разложением Тейлора .
Дискретизация экспоненциального распространения многошагового типа z n + 1 = z n + ϕ ( t n , z n ; h ) + h ∑ j = 0 p − 1 γ j ∇ j g n ( t n , z n ) , w i t h γ j = ( − 1 ) j ∫ 0 1 e ( 1 − θ ) h f x ( t n , z n ) ( − θ j ) d θ , {\textstyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h)+h\sum _{j=0}^{p-1}\gamma _{j}\nabla ^{j}\mathbf {g} _{n}(t_{n},\mathbf {z} _{n}),\quad with\quad \gamma _{j}=(-1)^{j}\int \limits _{0}^{1}e^{(1-\theta )h\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})}\left({\begin{array}{c}-\theta \\j\end{array}}\right)d\theta ,}
что является результатом интерполяции g n {\displaystyle \mathbf {g} _{n}} p на t n , … , t n − p + 1 {\displaystyle t_{n},\ldots ,t_{n-p+1}} ∇ j g n ( t m , z m ) {\displaystyle \nabla ^{j}\mathbf {g} _{n}(t_{m},\mathbf {z} _{m})} j -ю обратную разность g n ( t m , z m ) {\displaystyle \mathbf {g} _{n}(t_{m},\mathbf {z} _{m})}
Дискретизация экспоненциального распространения типа Рунге Кутты [7] z n + 1 = z n + ϕ ( t n , z n ; h ) + h ∑ j = 0 p − 1 γ j , p ∇ j g n ( t n , z n ) , with γ j , p = ∫ 0 1 e ( 1 − θ ) h f x ( t n , z n ) ( θ p j ) d θ , {\textstyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h)+h\sum _{j=0}^{p-1}\gamma _{j,p}\nabla ^{j}\mathbf {g} _{n}(t_{n},\mathbf {z} _{n}),\quad {\text{ with }}\quad \gamma _{j,p}=\int \limits _{0}^{1}e^{(1-\theta )h\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})}\left({\begin{array}{c}\theta p\\j\end{array}}\right)d\theta ,}
что является результатом интерполяции g n {\displaystyle \mathbf {g} _{n}} p на t n , … , t n + ( p − 1 ) h / p {\displaystyle t_{n},\ldots ,t_{n}+(p-1)h/p}
Линеализованная экспоненциальная дискретизация Адамса [8] z n + 1 = z n + ϕ ( t n , z n ; h ) + h ∑ j = 1 p − 1 ∑ l = 1 j γ j + 1 l ∇ l g n ( t n , z n ) , with γ j + 1 = ( − 1 ) j + 1 ∫ 0 1 e ( 1 − θ ) h f x ( t n , z n ) θ ( − θ j ) d θ , {\textstyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h)+h\sum _{j=1}^{p-1}\sum _{l=1}^{j}{\frac {\gamma _{j+1}}{l}}\nabla ^{l}\mathbf {g} _{n}(t_{n},\mathbf {z} _{n}),\quad {\text{ with }}\quad \gamma _{j+1}=(-1)^{j+1}\int \limits _{0}^{1}e^{(1-\theta )h\mathbf {f} _{\mathbf {x} }\left(t_{n},\mathbf {z} _{n}\right)}\theta \left({\begin{array}{c}-\theta \\j\end{array}}\right)d\theta ,}
что является результатом интерполяции g n {\displaystyle \mathbf {g} _{n}} Эрмита степени p на t n , … , t n − p + 1 {\displaystyle t_{n},\ldots ,t_{n-p+1}}
Схемы локальной линеаризации [ править ] Вся численная реализация y n {\displaystyle \mathbf {y} _{n}} z n {\displaystyle \mathbf {z} _{n}} ϕ ~ j {\displaystyle {\widetilde {\phi }}_{j}} ϕ j {\displaystyle \phi _{j}}
ϕ j ( A , h ) = ∫ 0 h e ( h − s ) A s j − 1 d s , j = 1 , 2 … , {\displaystyle \phi _{j}(\mathbf {A} ,h)=\int \limits _{0}^{h}e^{(h-s)\mathbf {A} }s^{j-1}\,ds,\qquad j=1,2\ldots ,}
где A — матрица размера d × d . Каждая численная реализация y n {\displaystyle \mathbf {y} _{n}} z n {\displaystyle \mathbf {z} _{n}} схемой локальной линеаризации . [1] [9]
Вычисление интегралов с экспоненты использованием матричной Среди ряда алгоритмов вычисления интегралов ϕ j {\displaystyle \phi _{j}} [10] [5] [11]
∑ i = 1 l ϕ i ( A , h ) a i = L e h H r , {\displaystyle \sum \nolimits _{i=1}^{l}\phi _{i}(\mathbf {A} ,h)\mathbf {a} _{i}=\mathbf {L} e^{h\mathbf {H} }\mathbf {r} ,}
где a i {\displaystyle \mathbf {a} _{i}} d -мерными векторами,
H = [ A v l v l − 1 ⋯ v 1 0 0 1 ⋯ 0 0 0 0 ⋱ 0 ⋮ ⋮ ⋮ ⋱ 1 0 0 0 ⋯ 0 ] ∈ R ( d + l ) × ( d + l ) , {\displaystyle \mathbf {H} ={\begin{bmatrix}\mathbf {A} &\mathbf {v} _{l}&\mathbf {v} _{l-1}&\cdots &\mathbf {v} _{1}\\\mathbf {0} &\mathbf {0} &1&\cdots &0\\\mathbf {0} &\mathbf {0} &0&\ddots &0\\\vdots &\vdots &\vdots &\ddots &1\\\mathbf {0} &\mathbf {0} &0&\cdots &0\end{bmatrix}}\in \mathbb {R} ^{(d+l)\times (d+l)},}
L = [ I 0 d × l ] {\displaystyle \mathbf {L} =[\mathbf {I} \quad \mathbf {0} _{d\times l}]} r = [ 0 1 × ( d + l − 1 ) 1 ] ⊺ , {\displaystyle \mathbf {r} =[\mathbf {0} _{1\times (d+l-1)}\quad 1]^{\intercal },} v i = a i ( i − 1 ) ! {\displaystyle \mathbf {v} _{i}=\mathbf {a} _{i}(i-1)!} I {\displaystyle \mathbf {I} } d .
Если P p , q ( 2 − k H h ) {\displaystyle \mathbf {P} _{p,q}(2^{-k}\mathbf {H} h)} p ; q ) Паде -аппроксимацию e 2 − k H h {\displaystyle e^{2^{-k}\mathbf {H} h}} k — наименьшее натуральное число такое, что | 2 − k H h | ≤ 1 2 , t h e n {\displaystyle |2^{-k}\mathbf {H} h|\leq {\frac {1}{2}},then} [12] [9]
| ∑ i = 1 l ϕ i ( A , h ) a i − L ( P p , q ( 2 − k H h ) ) 2 k r | ∝ h p + q + 1 . {\displaystyle \left\vert \sum \nolimits _{i=1}^{l}\phi _{i}(\mathbf {A} ,h)\mathbf {a} _{i}-\mathbf {L} \left(\mathbf {\mathbf {P} } _{p,q}(2^{-k}\mathbf {H} h)\right)^{2^{k}}\mathbf {r} \right\vert \varpropto h^{p+q+1}.}
Если k m , k p , q ( h , H , r ) {\displaystyle \mathbf {\mathbf {k} } _{m,k}^{p,q}(h,\mathbf {H} ,\mathbf {r} )} (m; p; q; k) Крылова–Паде аппроксимацию e h H r {\displaystyle e^{h\mathbf {H} }\mathbf {r} } [12]
| ∑ i = 1 l ϕ i ( A , h ) a i − L k m , k p , q ( h , H , r ) | ∝ h min ( m , p + q + 1 ) , {\displaystyle \left\vert \sum \nolimits _{i=1}^{l}\phi _{i}(\mathbf {A} ,h)\mathbf {a} _{i}-\mathbf {L\mathbf {k} } _{m,k}^{p,q}(h,\mathbf {H} ,\mathbf {r} )\right\vert \varpropto h^{\min({m,p+q+1})},}
где m ≤ d {\displaystyle m\leq d}
Схемы ЛЛ Ордена-2 [ править ] y n + 1 = y n + L ( P p , q ( 2 − k n M n h n ) ) 2 k n r , {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r,} } [13] [9] ( 4.6 ) {\displaystyle \qquad \qquad (4.6)}
где матрицы M n {\displaystyle \mathbf {M} _{n}} L и r определяются как
M n = [ f x ( t n , y n ) f t ( t n , y n ) f ( t n , y n ) 0 0 1 0 0 0 ] ∈ R ( d + 2 ) × ( d + 2 ) , {\displaystyle \mathbf {M} _{n}={\begin{bmatrix}\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {y} _{n})&\mathbf {f} _{t}(t_{n},\mathbf {y} _{n})&\mathbf {f} (t_{n},\mathbf {y} _{n})\\0&0&1\\0&0&0\end{bmatrix}}\in \mathbb {R} ^{(d+2)\times (d+2)},}
L = [ I 0 d × 2 ] {\displaystyle \mathbf {L} =\left[{\begin{array}{ll}\mathbf {I} &\mathbf {0} _{d\times 2}\end{array}}\right]} r ⊺ = [ 0 1 × ( d + 1 ) 1 ] {\displaystyle \mathbf {r} ^{\intercal }=\left[{\begin{array}{ll}\mathbf {0} _{1\times (d+1)}&1\end{array}}\right]} p + q > 1 {\displaystyle p+q>1} [3]
y n + 1 = y n + L k m n , k n p , q ( h n , M n , r ) , with m n > 2. {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L\mathbf {k} } _{m_{n},k_{n}}^{p,q}(h_{n},\mathbf {M} _{n},\mathbf {r} )\mathbf {,} \qquad {\text{ with }}\qquad m_{n}>2.}
Схемы Ордена-3 LL-Тейлора [ править ] y n + 1 = y n + L 1 ( P p , q ( 2 − k n T n h n ) ) 2 k n r 1 , {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L} _{1}(\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {T} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r} _{1}\mathbf {,} } [5] ( 4.7 ) {\displaystyle \qquad \qquad (4.7)}
где для автономных ОДУ матрицы T n , L 1 {\displaystyle \mathbf {T} _{n},\mathbf {L} _{1}} r 1 {\displaystyle \mathbf {r} _{1}}
T n = [ f x ( y n ) ( I ⊗ f ⊺ ( y n ) ) f x x ( y n ) f ( y n ) 0 f ( y n ) 0 0 0 0 0 0 0 1 0 0 0 0 ] ∈ R ( d + 3 ) × ( d + 3 ) , {\displaystyle \mathbf {T} _{n}=\left[{\begin{array}{cccc}\mathbf {f} _{\mathbf {x} }(\mathbf {y} _{n})&(\mathbf {I} \otimes \mathbf {f} ^{\intercal }(\mathbf {y} _{n}))\mathbf {f} _{\mathbf {xx} }(\mathbf {y} _{n})\mathbf {f} (\mathbf {y} _{n})&\mathbf {0} &\mathbf {f} (\mathbf {y} _{n})\\0&0&0&0\\0&0&0&1\\0&0&0&0\end{array}}\right]\in \mathbb {R} ^{(d+3)\times (d+3)},}
L 1 = [ I 0 d × 3 ] a n d r 1 ⊺ = [ 0 1 × ( d + 2 ) 1 ] {\displaystyle \mathbf {L} _{1}=\left[{\begin{array}{ll}\mathbf {I} &\mathbf {0} _{d\times 3}\end{array}}\right]\quad and\quad \mathbf {r} _{1}^{\intercal }=\left[{\begin{array}{ll}\mathbf {0} _{1\times (d+2)}&1\end{array}}\right]} f x x {\displaystyle \mathbf {f} _{\mathbf {xx} }} f по x и p + q > 2 . Для больших систем ОДУ
y n + 1 = y n + L k m n , k n p , q ( h n , T n , r ) , with m n > 3. {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L\mathbf {k} } _{m_{n},k_{n}}^{p,q}(h_{n},\mathbf {T} _{n},\mathbf {r} )\mathbf {,} \qquad {\text{ with }}\qquad m_{n}>3.}
Схемы ЛЛ-РК Приказ-4 [ править ] y n + 1 = y n + u 4 + h n 6 ( 2 k 2 + 2 k 3 + k 4 ) , {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {u} _{4}+{\frac {h_{n}}{6}}(2\mathbf {k} _{2}+2\mathbf {k} _{3}+\mathbf {k} _{4}),\quad } [4] [6] ( 4.8 ) {\displaystyle \qquad \qquad (4.8)}
где
u j = L ( P p , q ( 2 − κ j M n c j h n ) ) 2 κ j r {\displaystyle \mathbf {u} _{j}=\mathbf {L} (\mathbf {P} _{p,q}(2^{-\kappa _{j}}\mathbf {M} _{n}c_{j}h_{n}))^{2^{\kappa _{j}}}\mathbf {r} }
и
k j = f ( t n + c j h n , y n + u j + c j h n k j − 1 ) − f ( t n , y n ) − f x ( t n , y n ) u j − f t ( t n , y n ) c j h n , {\displaystyle \mathbf {k} _{j}=\mathbf {f} \left(t_{n}+c_{j}h_{n},\mathbf {y} _{n}+\mathbf {u} _{j}+c_{j}h_{n}\mathbf {k} _{j-1}\right)-\mathbf {f} \left(t_{n},\mathbf {y} _{n}\right)-\mathbf {f} _{\mathbf {x} }\left(t_{n},\mathbf {y} _{n}\right)\mathbf {u} _{j}\ -\mathbf {f} _{t}\left(t_{n},\mathbf {y} _{n}\right)c_{j}h_{n},}
с k 1 ≡ 0 , c = [ 0 1 2 1 2 1 ] , {\displaystyle \mathbf {k} _{1}\equiv \mathbf {0} ,c=\left[{\begin{array}{cccc}0&{\frac {1}{2}}&{\frac {1}{2}}&1\end{array}}\right],} р + q > 3 . Для больших систем ОДУ вектор u j {\displaystyle \mathbf {u} _{j}} u j = L k m j , k j p , q ( c j h n , M n , r ) {\displaystyle \mathbf {u} _{j}=\mathbf {L\mathbf {k} } _{m_{j},k_{j}}^{p,q}(c_{j}h_{n},\mathbf {M} _{n},\mathbf {r} )} m j > 4. {\displaystyle m_{j}>4.}
y n + 1 = y n + u s + h n ∑ j = 1 s b j k j and y ^ n + 1 = y n + u s + h n ∑ j = 1 s b ^ j k j , {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {u} _{s}+h_{n}\sum _{j=1}^{s}b_{j}\mathbf {k} _{j}\qquad {\text{ and }}\qquad {\widehat {\mathbf {y} }}_{n+1}=\mathbf {y} _{n}+\mathbf {u} _{s}+h_{n}\sum _{j=1}^{s}{\widehat {b}}_{j}\mathbf {k} _{j},\quad } [14] [15] ( 4.9 ) {\displaystyle \qquad \qquad (4.9)}
где s = 7 – количество ступеней,
k j = f ( t n + c j h n , y n + u j + h n ∑ i = 1 s − 1 a j , i k i ) − f ( t n , y n ) − f x ( t n , y n ) u j − f t ( t n , y n ) c j h n , {\displaystyle \mathbf {k} _{j}=\mathbf {f(} t_{n}+c_{j}h_{n},\mathbf {y} _{n}+\mathbf {u} _{j}+h_{n}\sum _{i=1}^{s-1}a_{j,i}\mathbf {k} _{i})-\mathbf {f} \left(t_{n},\mathbf {y} _{n}\right)-\mathbf {f} _{\mathbf {x} }\left(t_{n},\mathbf {y} _{n}\right)\mathbf {u} _{j}\ -\mathbf {f} _{t}\left(t_{n},\mathbf {y} _{n}\right)c_{j}h_{n},}
с k 1 ≡ 0 {\displaystyle \mathbf {k} _{1}\equiv \mathbf {0} } a j , i , b j , b ^ j a n d c j {\displaystyle a_{j,i},b_{j},{\widehat {b}}_{j}\quad and\quad c_{j}} коэффициенты Рунге–Кутты Дормана и Принса , p + q > 4. Вектор u j {\displaystyle \mathbf {u} _{j}}
Стабильность и динамика [ править ] Рис. 1 Фазовый портрет (пунктирная линия) и приближенный фазовый портрет (сплошная линия) нелинейного ОДУ (4.10)-(4.11), рассчитанного по схеме LL 2-го порядка (4.2), классической схеме Рюгена-Кутты RK 4-го порядка 4 схемы LLRK 4 порядка 4 (4.8) с размером шага h=1/2 и p=q=6. По построению дискретизации LL и HOLL наследуют стабильность и динамику линейных ОДУ, но это не относится к схемам LL в целом. С p ≤ q ≤ p + 2 {\displaystyle p\leq q\leq p+2} A -стабильны [4] q = p + 1 или q = p + 2 ЛЛ-схемы (4.6)–(4.9) также являются L -стабильными [4] p + q . [4] [9] p = q = 6 и m n {\displaystyle m_{n}} d , все вышеописанные схемы LL поддаются «точному вычислению» (с точностью до арифметики с плавающей запятой ) линейных ОДУ на современных персональных компьютерах. [4] [9] жесткие и сильно колебательные линейные уравнения. Более того, ЛЛ-схемы (4.6)-(4.9) регулярны для линейных ОДУ и наследуют симплектическую структуру гамильтоновых гармонических осцилляторов . [5] [13] устойчивых и неустойчивых многообразий вокруг гиперболических точек равновесия и периодических орбит , чем другие численные схемы с тем же размером шага. [5] [13] фазовый портрет ОДУ
d x 1 d t = − 2 x 1 + x 2 + 1 − μ f ( x 1 , λ ) ( 4.10 ) d x 2 d t = x 1 − 2 x 2 + 1 − μ f ( x 2 , λ ) ( 4.11 ) {\displaystyle {\begin{aligned}&{\frac {dx_{1}}{dt}}=-2x_{1}+x_{2}+1-\mu f(x_{1},\lambda )\qquad \qquad (4.10)\\[6pt]&{\frac {dx_{2}}{dt}}=x_{1}-2x_{2}+1-\mu f(x_{2},\lambda )\qquad \qquad \quad (4.11)\end{aligned}}} с f ( u , λ ) = u ( 1 + u + λ u 2 ) − 1 {\displaystyle f(u,\lambda )=u(1+u+\lambda u^{2})^{-1}} μ = 15 {\displaystyle \mu =15} λ = 57 {\displaystyle \lambda =57} устойчивые стационарные точки и одну неустойчивую стационарную точку в области 0 ≤ x 1 , x 2 ≤ 1 {\displaystyle 0\leq x_{1},x_{2}\leq 1}
Методы LL для DDE [ править ] Рассмотрим d -мерное дифференциальное уравнение с запаздыванием (DDE).
d x ( t ) d t = f ( t , x ( t ) , x t ( − τ 1 ) , … , x t ( − τ m ) ) , t ∈ [ t 0 , T ] , ( 5.1 ) {\displaystyle {\frac {d\mathbf {x} (t)}{dt}}=\mathbf {f} (t,\mathbf {x} (t),\mathbf {x} _{t}(-\tau _{1}),\ldots ,\mathbf {x} _{t}(-\tau _{m})),\qquad t\in [t_{0},T],\qquad \qquad (5.1)}
с m постоянными задержками τ i > 0 {\displaystyle \tau _{i}>0} x t 0 ( s ) = φ ( s ) {\displaystyle \mathbf {x} _{t_{0}}(s)=\mathbf {\varphi } (s)} s ∈ [ − τ , 0 ] , {\displaystyle s\in [-\tau ,0],} f — дифференцируемая функция, x t : [ − τ , 0 ] ⟶ R d {\displaystyle \mathbf {x} _{t}:[-\tau ,0]\longrightarrow \mathbb {R} ^{d}}
x t ( s ) := x ( t + s ) , s ∈ [ − τ , 0 ] , {\displaystyle \mathbf {x} _{t}(s):=\mathbf {x} (t+s),{\text{ }}s\in [-\tau ,0],}
для всех t ∈ [ t 0 , T ] , φ : [ − τ , 0 ] ⟶ R d {\displaystyle t\in [t_{0},T],\mathbf {\varphi } :[-\tau ,0]\longrightarrow \mathbb {R} ^{d}} τ = max { τ 1 , … , τ m } . {\displaystyle \tau =\max \left\{\tau _{1},\ldots ,\tau _{m}\right\}.}
Локальная дискретизация линейная Для временной дискретизации ( t ) h {\displaystyle (t)_{h}} Локальная линейная дискретизация ДДУ (5.1) в каждой точке t n + 1 ∈ ( t ) h {\displaystyle t_{n+1}\in (t)_{h}} [11]
z n + 1 = z n + Φ ( t n , z n , h n ; z ~ t n 1 , … , z ~ t n m ) , ( 5.2 ) {\displaystyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\Phi (t_{n},\mathbf {z} _{n},h_{n};{\widetilde {\mathbf {z} }}_{t_{n}}^{1},\ldots ,{\widetilde {\mathbf {z} }}_{t_{n}}^{m}),\qquad \qquad (5.2)}
где
Φ ( t n , z n , h n ; z ~ t n 1 , … , z ~ t n m ) = ∫ 0 h n e A n ( h n − u ) [ ∑ i = 1 m B n i ( z ~ t n i ( u − τ i ) − z ~ t n i ( − τ i ) ) + d n ] d u + ∫ 0 h n ∫ 0 u e A n ( h n − u ) c n d r d u {\displaystyle \Phi (t_{n},\mathbf {z} _{n},h_{n};{\widetilde {\mathbf {z} }}_{t_{n}}^{1},\ldots ,{\widetilde {\mathbf {z} }}_{t_{n}}^{m})=\int \limits _{0}^{h_{n}}e^{\mathbf {A} _{n}(h_{n}-u)}\left[\sum \limits _{i=1}^{m}\mathbf {B} _{n}^{i}({\widetilde {\mathbf {z} }}_{t_{n}}^{i}(u-\tau _{i})-{\widetilde {\mathbf {z} }}_{t_{n}}^{i}(-\tau _{i}))+\mathbf {d} _{n}\right]\,du+\int \limits _{0}^{h_{n}}\int \limits _{0}^{u}e^{\mathbf {A} _{n}(h_{n}-u)}\mathbf {c} _{n}\,dr\,du}
z ~ t n i : [ − τ i , 0 ] ⟶ R d {\displaystyle {\widetilde {\mathbf {z} }}_{t_{n}}^{i}:\left[-\tau _{i},0\right]\longrightarrow \mathbb {R} ^{d}}
z ~ t n i ( s ) := z ~ i ( t n + s ) , s ∈ [ − τ i , 0 ] , {\displaystyle {\widetilde {\mathbf {z} }}_{t_{n}}^{i}(s):={\widetilde {\mathbf {z} }}^{i}(t_{n}+s),{\text{ }}s\in [-\tau _{i},0],}
и z ~ i : [ t n − τ i , t n ] ⟶ R d {\displaystyle {\widetilde {\mathbf {z} }}^{i}:\left[t_{n}-\tau _{i},t_{n}\right]\longrightarrow \mathbb {R} ^{d}} x ( t ) {\displaystyle \mathbf {x} (t)} t ∈ [ t n − τ i , t n ] {\displaystyle t\in \lbrack t_{n}-\tau _{i},t_{n}]} z ~ i ( t n ) = z n . {\displaystyle {\widetilde {\mathbf {z} }}^{i}(t_{n})=\mathbf {z} _{n}.}
A n = f x ( t n , z n , z ~ t n 1 ( − τ 1 ) , … , z ~ t n m ( − τ d ) ) , B n i = f x t ( − τ i ) ( t n , z n , z ~ t n 1 ( − τ 1 ) , … , z ~ t n m ( − τ d ) ) {\displaystyle \mathbf {A} _{n}=\mathbf {f} _{x}(t_{n},\mathbf {z} _{n},{\widetilde {\mathbf {z} }}_{t_{n}}^{1}(-\tau _{1}),\ldots ,{\widetilde {\mathbf {z} }}_{t_{n}}^{m}(-\tau _{d})),{\text{ }}\mathbf {B} _{n}^{i}=\mathbf {f} _{x_{t}(-\tau _{i})}(t_{n},\mathbf {z} _{n},{\widetilde {\mathbf {z} }}_{t_{n}}^{1}(-\tau _{1}),\ldots ,{\widetilde {\mathbf {z} }}_{t_{n}}^{m}(-\tau _{d}))}
являются постоянными матрицами и
c n = f t ( t n , z n , z ~ t n 1 ( − τ 1 ) , … , z ~ t n m ( − τ d ) ) and d n = f ( t n , z n , z ~ t n 1 ( − τ 1 ) , … , z ~ t n m ( − τ d ) ) {\displaystyle \mathbf {c} _{n}=\mathbf {f} _{t}(t_{n},\mathbf {z} _{n},{\widetilde {\mathbf {z} }}_{t_{n}}^{1}(-\tau _{1}),\ldots ,{\widetilde {\mathbf {z} }}_{t_{n}}^{m}(-\tau _{d})){\text{ and }}\mathbf {d} _{n}=\mathbf {f(} t_{n},\mathbf {z} _{n},{\widetilde {\mathbf {z} }}_{t_{n}}^{1}(-\tau _{1}),\ldots ,{\widetilde {\mathbf {z} }}_{t_{n}}^{m}(-\tau _{d}))}
являются постоянными векторами. f t , f x a n d f x t ( − τ i ) {\displaystyle \mathbf {f} _{t},\mathbf {f} _{x}\quad and\quad \mathbf {f} _{x_{t}(-\tau _{i})}} f по переменным t и x x t ( − τ i ) {\displaystyle \mathbf {x} _{t}(-\tau _{i})} α = min { 2 , r } , {\displaystyle \alpha =\min\{2,r\},} z ~ t n i {\displaystyle {\widetilde {\mathbf {z} }}_{t_{n}}^{i}} z t n i {\displaystyle \mathbf {z} _{t_{n}}^{i}} r ( i . e . , | z t n i ( u − τ i ) − z ~ t n i ( u − τ i ) | ∝ h n r {\displaystyle r\quad (i.e.,\left\vert \mathbf {z} _{t_{n}}^{i}\mathbf {(} u-\tau _{i}\mathbf {)} -{\widetilde {\mathbf {z} }}_{t_{n}}^{i}\mathbf {(} u-\tau _{i}\mathbf {)} \right\vert \propto h_{n}^{r}} u ∈ [ 0 , h n ] ) {\displaystyle u\in \lbrack 0,h_{n}])}
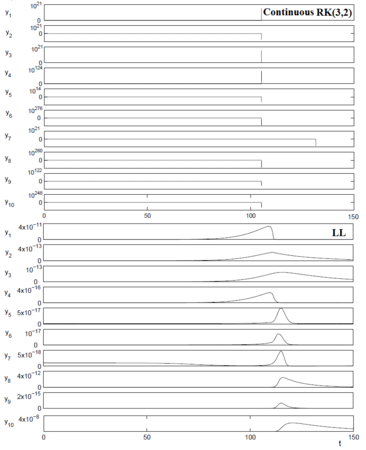
Схемы локальной линеаризации [ править ] Рис. 2. Примерные пути Марчука и др. (1991) противовирусная иммунная модель, описываемая жесткой системой десятимерных нелинейных DDE с пятью временными задержками: вверху — Рунге–Кутты (2,3) непрерывная схема ; внизу — схема ЛЛ (5.3). Размер шага h = 0,01 фиксированный, а p = q = 6. В зависимости от приближений z ~ t n i {\displaystyle {\widetilde {\mathbf {z} }}_{t_{n}}^{i}} ϕ {\displaystyle \mathbf {\phi } } y n {\displaystyle \mathbf {y} _{n}} z n {\displaystyle \mathbf {z} _{n}} схемой локальной линеаризации .
Схемы LL с полиномом 2-го порядка [ править ] y n + 1 = y n + L ( P p , q ( 2 − k n M n h n ) ) 2 k n r , {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r,} \quad } [11] ( 5.3 ) {\displaystyle \qquad (5.3)}
где матрицы M n , L {\displaystyle \mathbf {M} _{n},\mathbf {L} } r {\displaystyle \mathbf {r} }
M n = [ A n c n + ∑ i = 1 m B n i α n i d n 0 0 1 0 0 0 ] ∈ R ( d + 2 ) × ( d + 2 ) , {\displaystyle \mathbf {M} _{n}={\begin{bmatrix}\mathbf {A} _{n}&\mathbf {c} _{n}+\sum \limits _{i=1}^{m}\mathbf {B} _{n}^{i}\mathbf {\alpha } _{n}^{i}&\mathbf {d} _{n}\\0&0&1\\0&0&0\end{bmatrix}}\in \mathbb {R} ^{(d+2)\times (d+2)},}
L = [ I 0 d × 2 ] {\displaystyle \mathbf {L} =\left[{\begin{array}{ll}\mathbf {I} &\mathbf {0} _{d\times 2}\end{array}}\right]} r ⊺ = [ 0 1 × ( d + 1 ) 1 ] , h n ≤ τ {\displaystyle \mathbf {r} ^{\intercal }=\left[{\begin{array}{ll}\mathbf {0} _{1\times (d+1)}&1\end{array}}\right],h_{n}\leq \tau } p + q > 1 {\displaystyle p+q>1} A n {\displaystyle \mathbf {A} _{n}} B n i {\displaystyle \mathbf {B} _{n}^{i}} c n {\displaystyle \mathbf {c} _{n}} d n {\displaystyle \mathbf {d} _{n}} z {\displaystyle \mathbf {z} } y {\displaystyle \mathbf {y} } α n i = ( y ( t n + 1 − τ i ) − y ( t n − τ i ) ) / h n , {\displaystyle \mathbf {\alpha } _{n}^{i}=(\mathbf {y} (t_{n+1}-\tau _{i})-\mathbf {y} (t_{n}-\tau _{i}))/h_{n},}
y ( t ) = y n t + L ( P p , q ( 2 − k n M n t ( t − t n t ) ) ) 2 k n r , {\displaystyle \mathbf {y} \left(t\right)=\mathbf {y} _{n_{t}}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n_{t}}(t-t_{n_{t}})))^{2^{k_{n}}}\mathbf {r} ,}
с n t = max { n = 0 , 1 , 2 , . . . , : t n ≤ t and t n ∈ ( t ) h } {\displaystyle n_{t}=\max\{n=0,1,2,...,:t_{n}\leq t{\text{ and }}t_{n}\in \left(t\right)_{h}\}} локальная линейная аппроксимация решения (5.1), определенная с помощью схемы ЛЛ (5.3) для всех t ∈ [ t 0 , t n ] {\displaystyle t\in \lbrack t_{0},t_{n}]} y ( t ) = φ ( t ) {\displaystyle \mathbf {y} \left(t\right)=\mathbf {\varphi } \left(t\right)} t ∈ [ t 0 − τ , t 0 ] {\displaystyle t\in \left[t_{0}-\tau ,t_{0}\right]}
y n + 1 = y n + L k m n , k n p , q ( h n , M n , r ) a n d y ( t ) = y n t + L k m n t , k n t p , q ( t − t n t , M n t , r ) , {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L\mathbf {k} } _{m_{n},k_{n}}^{p,q}(h_{n},\mathbf {M} _{n},\mathbf {r} )\quad and\quad \mathbf {y} \left(t\right)=\mathbf {y} _{n_{t}}+\mathbf {L\mathbf {k} } _{m_{n_{t}},k_{n_{t}}}^{p,q}(t-t_{n_{t}},\mathbf {M} _{n_{t}},\mathbf {r} ),}
с p + q > 1 {\displaystyle p+q>1} m n > 2 {\displaystyle m_{n}>2}
Методы LL для RDE [ править ] Рассмотрим d -мерное случайное дифференциальное уравнение (СДУ)
d x ( t ) d t = f ( x ( t ) , ξ ( t ) ) , t ∈ [ t 0 , T ] , ( 6.1 ) {\displaystyle {\frac {d\mathbf {x} \left(t\right)}{dt}}=\mathbf {f} (\mathbf {x} (t),\mathbf {\xi } (t)),\quad t\in \left[t_{0},T\right],\qquad \qquad \qquad (6.1)} с начальным состоянием x ( t 0 ) = x 0 , {\displaystyle \mathbf {x} (t_{0})=\mathbf {x} _{0},} ξ {\displaystyle \mathbf {\xi } } k -мерный сепарабельный конечный непрерывный случайный процесс , а f — дифференцируемая функция. Предположим, что реализация (путь) ξ {\displaystyle \mathbf {\xi } }
Локальная дискретизация линейная Для временной дискретизации ( t ) h {\displaystyle \left(t\right)_{h}} Локальная линейная дискретизация РДУ (6.1) в каждой точке t n + 1 ∈ ( t ) h {\displaystyle t_{n+1}\in \left(t\right)_{h}} [16]
z n + 1 = z n + ϕ ( t n , z n ; h n ) , with z 0 = x 0 , {\displaystyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h_{n}),\qquad {\text{ with }}\qquad \mathbf {z} _{0}=\mathbf {x} _{0},}
где
ϕ ( t n , z n ; h n ) = ∫ 0 h n e f x ( z n , ξ ( t n ) ) ( h n − u ) ( f ( z n , ξ ( t n ) ) + f ξ ( z n , ξ ( t n ) ) ( ξ ~ ( t n + u ) − ξ ~ ( t n ) ) ) d u {\displaystyle \mathbf {\phi } (t_{n},\mathbf {z} _{n};h_{n})=\int \limits _{0}^{h_{n}}e^{\mathbf {f} _{\mathbf {x} }(\mathbf {z} _{n},\mathbf {\xi } (t_{n}))(h_{n}-u)}(\mathbf {f(z} _{n},\mathbf {\xi } (t_{n}))+\mathbf {f} _{\mathbf {\xi } }(\mathbf {z} _{n},\mathbf {\xi } (t_{n}))({\widetilde {\mathbf {\xi } }}(t_{n}+u)-{\widetilde {\mathbf {\xi } }}(t_{n})))\,du}
и ξ ~ {\displaystyle {\widetilde {\mathbf {\xi } }}} ξ {\displaystyle \mathbf {\xi } } t ∈ [ t 0 , T ] . {\displaystyle t\in \left[t_{0},T\right].} f x {\displaystyle \mathbf {f} _{x}} f ξ {\displaystyle \mathbf {f} _{\xi }} f {\displaystyle \mathbf {f} } x {\displaystyle \mathbf {x} } ξ {\displaystyle \xi }
Схемы локальной линеаризации [ править ] Рис. 3. Фазовый портрет траекторий схем Эйлера и ЛЛ при интегрировании нелинейного СДУ (6.2)–(6.3) с размером шага h = 1/32 и p = q = 6. В зависимости от приближений ξ ~ {\displaystyle {\widetilde {\mathbf {\xi } }}} ξ {\displaystyle \mathbf {\xi } } ϕ {\displaystyle \mathbf {\phi } } y n {\displaystyle \mathbf {y} _{n}} z n {\displaystyle \mathbf {z} _{n}} схемой локальной линеаризации.
y n + 1 = y n + L ( P p , q ( 2 − k n M n h n ) ) 2 k n r , {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r,} \quad } [16] [17] где матрицы M n , L a n d r {\displaystyle \mathbf {M} _{n},\quad \mathbf {L} \quad and\quad \mathbf {r} }
M n = [ f x ( y n , ξ ( t n ) ) f ξ ( y n , ξ ( t n ) ( ξ ( t n + 1 ) − ξ ( t n ) ) / h n f ( y n , ξ ( t n ) ) 0 0 1 0 0 0 ] {\displaystyle \mathbf {M} _{n}=\left[{\begin{array}{ccc}\mathbf {f} _{\mathbf {x} }\left(\mathbf {y} _{n},\mathbf {\xi } (t_{n})\right)&\mathbf {f} _{\mathbf {\xi } }(\mathbf {y} _{n},\mathbf {\xi } (t_{n})(\mathbf {\xi } (t_{n+1})-\mathbf {\xi } (t_{n}))/h_{n}&\mathbf {f} \left(\mathbf {y} _{n},\mathbf {\xi } (t_{n})\right)\\0&0&1\\0&0&0\end{array}}\right]}
L = [ I 0 d × 2 ] {\displaystyle \mathbf {L} =\left[{\begin{array}{ll}\mathbf {I} &\mathbf {0} _{d\times 2}\end{array}}\right]} r ⊺ = [ 0 1 × ( d + 1 ) 1 ] {\displaystyle \mathbf {r} ^{\intercal }=\left[{\begin{array}{ll}\mathbf {0} _{1\times (d+1)}&1\end{array}}\right]} p+q>1 . Для больших систем RDE [17]
y n + 1 = y n + L k m n , k n p , q ( h n , M n , r ) , p + q > 1 a n d m n > 2. {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L\mathbf {k} } _{m_{n},k_{n}}^{p,q}(h_{n},\mathbf {M} _{n},\mathbf {r} ),\quad p+q>1\quad and\quad m_{n}>2.}
Скорость сходимости обеих схем равна m i n { 2 , 2 γ } {\displaystyle min\{2,2\gamma \}} γ {\displaystyle \gamma } ξ {\displaystyle \mathbf {\xi } }
На рис. 3 представлен фазовый портрет РДЭ.
d x 1 d t = − x 2 + ( 1 − x 1 2 − x 2 2 ) x 1 sin ( w H ( t ) ) 2 , x 1 ( 0 ) = 0.8 ( 6.2 ) {\displaystyle {\frac {dx_{1}}{dt}}=-x_{2}+\left(1-x_{1}^{2}-x_{2}^{2}\right)x_{1}\sin(w^{H}(t))^{2},\quad \qquad x_{1}(0)=0.8\qquad (6.2)}
d x 2 d t = x 1 + ( 1 − x 1 2 − x 2 2 ) x 2 sin ( w H ( t ) ) 2 , x 2 ( 0 ) = 0.1 , ( 6.3 ) {\displaystyle {\frac {dx_{2}}{dt}}=x_{1}+(1-x_{1}^{2}-x_{2}^{2})x_{2}\sin(w^{H}(t))^{2},\qquad \qquad x_{2}(0)=0.1,\qquad (6.3)}
и ее аппроксимация двумя численными схемами, где w H {\displaystyle w^{H}} дробный броуновский процесс с показателем Херста H=0,45 .
методы LL SDE для Сильные Рассмотрим d -мерное стохастическое дифференциальное уравнение (СДУ)
d x ( t ) = f ( t , x ( t ) ) d t + ∑ i = 1 m g i ( t ) d w i ( t ) , t ∈ [ t 0 , T ] , ( 7.1 ) {\displaystyle d\mathbf {x} (t)=\mathbf {f} (t,\mathbf {x} (t))dt+\sum \limits _{i=1}^{m}\mathbf {g} _{i}(t)d\mathbf {w} ^{i}(t),\quad t\in \left[t_{0},T\right],\qquad \qquad \qquad (7.1)}
с начальным состоянием x ( t 0 ) = x 0 {\displaystyle \mathbf {x} (t_{0})=\mathbf {x} _{0}} f {\displaystyle \mathbf {f} } g i {\displaystyle \mathbf {g} _{i}} w = ( w 1 , … , w m ) {\displaystyle \mathbf {w=(\mathbf {w} } ^{1},\ldots ,\mathbf {w} ^{m}\mathbf {)} } m -мерным стандартным винеровским процессом .
Локальная дискретизация линейная Для временной дискретизации ( t ) h {\displaystyle \left(t\right)_{h}} γ {\displaystyle \mathbb {\gamma } } Сильная локальная линейная дискретизация решения СДУ (7.1) определяется рекуррентным соотношением [18] [19]
z n + 1 = z n + ϕ γ ( t n , z n ; h n ) + ξ ( t n , z n ; h n ) , w i t h z 0 = x 0 , {\displaystyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } _{\mathbb {\gamma } }(t_{n},\mathbf {z} _{n};h_{n})+\mathbf {\xi } (t_{n},\mathbf {z} _{n};h_{n}),\quad with\quad \mathbf {z} _{0}=\mathbf {x} _{0},}
где
ϕ γ ( t n , z n ; δ ) = ∫ 0 δ e f x ( t n , y n ) ( δ − u ) ( f ( t n , z n ) + a γ ( t n , z n ) u ) d u {\displaystyle \mathbf {\phi } _{\mathbb {\gamma } }(t_{n},\mathbf {z} _{n};\delta )=\int _{0}^{\delta }e^{\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {y} _{n})(\delta -u)}(\mathbf {f(} t_{n},\mathbf {z} _{n})+\mathbf {a} ^{\mathbb {\gamma } }(t_{n},\mathbf {z} _{n})u)du}
и
ξ ( t n , z n ; δ ) = ∑ i = 1 m ∫ t n t n + δ e f x ( t n , z n ) ( t n + δ − u ) g i ( u ) d w i ( u ) . {\displaystyle \mathbf {\xi } \left(t_{n},\mathbf {z} _{n};\delta \right)=\sum \limits _{i=1}^{m}\int \nolimits _{t_{n}}^{t_{n}+\delta }e^{\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})(t_{n}+\delta -u)}\mathbf {g} _{i}(u)\,d\mathbf {w} ^{i}(u).}
Здесь,
a γ ( t n , z n ) = { f t ( t n , z n ) for γ = 1 f t ( t n , z n ) + 1 2 ∑ j = 1 m ( I ⊗ g j ⊺ ( t n ) ) f x x ( t n , z n ) g j ( t n ) for γ = 1.5 , {\displaystyle \mathbf {a} ^{\mathbb {\gamma } }(t_{n},\mathbf {z} _{n})=\left\{{\begin{array}{cl}\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})&{\text{for }}\qquad \mathbb {\gamma } =1\\\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})+{\frac {1}{2}}\sum \limits _{j=1}^{m}(\mathbf {I} \otimes \mathbf {g} _{j}^{\intercal }(t_{n}))\mathbf {f} _{\mathbf {xx} }(t_{n},\mathbf {z} _{n})\mathbf {g} _{j}(t_{n})&{\text{for }}\quad \mathbb {\gamma } =1.5,\end{array}}\right.}
f x , f t {\displaystyle \mathbf {f} _{\mathbf {x} },\mathbf {f} _{t}} f {\displaystyle \mathbf {f} } x {\displaystyle \mathbf {x} } t f x x {\displaystyle \mathbf {f} _{\mathbf {xx} }} f {\displaystyle \mathbf {f} } x {\displaystyle \mathbf {x} } z n + 1 {\displaystyle \mathbf {z} _{n+1}} сходится с порядком γ {\displaystyle \mathbb {\gamma } }
высокого порядка дискретизация Локальная линейная После локальной линеаризации дрейфового члена (7.1) при ( t n , z n ) {\displaystyle (t_{n},\mathbf {z} _{n})} r {\displaystyle \mathbf {r} }
d r ( t ) = q γ ( t n , z n ; t , r ( t ) ) d t + ∑ i = 1 m g i ( t ) d w i ( t ) , r ( t n ) = 0 {\displaystyle d\mathbf {r} (t)=\mathbf {q} _{\gamma }(t_{n},\mathbf {z} _{n};t\mathbf {,\mathbf {r} } (t))\,dt+\sum \limits _{i=1}^{m}\mathbf {g} _{i}(t)\,d\mathbf {w} ^{i}(t)\mathbf {,} \qquad \mathbf {r} (t_{n})=\mathbf {0} }
для всех t ∈ [ t n , t n + 1 ] {\displaystyle t\in \lbrack t_{n},t_{n+1}]}
q γ ( t n , z n ; s , ξ ) = f ( s , z n + ϕ γ ( t n , z n ; s − t n ) + ξ ) − f x ( t n , z n ) ϕ γ ( t n , z n ; s − t n ) − a γ ( t n , z n ) ( s − t n ) − f ( t n , z n ) . {\displaystyle \mathbf {q} _{\gamma }(t_{n},\mathbf {z} _{n};s\mathbf {,\xi } )=\mathbf {f} (s,\mathbf {z} _{n}+\mathbf {\phi } _{\gamma }(t_{n},\mathbf {z} _{n};s-t_{n})+\mathbf {\xi } )-\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})\mathbf {\phi } _{\gamma }(t_{n},\mathbf {z} _{n};s-t_{n})-\mathbf {a} ^{\gamma }(t_{n},\mathbf {z} _{n})(s-t_{n})-\mathbf {f} (t_{n},\mathbf {z} _{n}).}
Локальная линейная дискретизация высокого порядка СДУ (7.1) в каждой точке t n + 1 ∈ ( t ) h {\displaystyle t_{n+1}\in (t)_{h}} [20]
z n + 1 = z n + ϕ γ ( t n , z n ; h n ) + r ~ ( t n , z n ; h n ) , with z 0 = x 0 , {\displaystyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } _{\gamma }(t_{n},\mathbf {z} _{n};h_{n})+{\widetilde {\mathbf {r} }}(t_{n},\mathbf {z} _{n};h_{n}),\qquad {\text{ with }}\qquad \mathbf {z} _{0}=\mathbf {x} _{0},}
где r ~ {\displaystyle {\widetilde {\mathbf {r} }}} r {\displaystyle \mathbf {r} } α {\displaystyle \alpha } 1,5 . Сильная дискретизация ХОЛЛА. z n + 1 {\displaystyle \mathbf {z} _{n+1}} α {\displaystyle \alpha }
Схемы локальной линеаризации [ править ] В зависимости от способа расчета ϕ γ {\displaystyle \mathbf {\phi } _{\mathbb {\gamma } }} ξ {\displaystyle \mathbf {\xi } } r ~ {\displaystyle {\widetilde {\mathbf {r} }}} y n {\displaystyle \mathbf {y} _{n}} z n {\displaystyle \mathbf {z} _{n}} схемой сильной локальной линеаризации (SLL) .
Схемы SLL заказа 1 [ править ] y n + 1 = y n + L ( P p , q ( 2 − k n M n h n ) ) 2 k n r + ∑ i = 1 m g i ( t n ) Δ w n i , {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r+} \sum \limits _{i=1}^{m}\mathbf {g} _{i}(t_{n})\Delta \mathbf {w} _{n}^{i},\quad } [21] ( 7.2 ) {\displaystyle \qquad \qquad (7.2)}
где матрицы M n {\displaystyle \mathbf {M} _{n}} L {\displaystyle \mathbf {L} } r {\displaystyle \mathbf {r} } Δ w n i {\displaystyle \Delta \mathbf {w} _{n}^{i}} iid нулевое среднее гауссовской случайной величины с дисперсией h n {\displaystyle h_{n}} p + q > 1. Для больших систем СДУ [21] ( P p , q ( 2 − k n M n h n ) ) 2 k n r {\displaystyle (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r} } k m n , k n p , q ( h n , M n , r ) {\displaystyle \mathbf {\mathbf {k} } _{m_{n},k_{n}}^{p,q}(h_{n},\mathbf {M} _{n},\mathbf {r} )}
Схемы SLL заказа 1.5 [ править ] y n + 1 = y n + L ( P p , q ( 2 − k n M n h n ) ) 2 k n r + ∑ i = 1 m ( g i ( t n ) Δ w n i f x ( t n , y ~ n ) g i ( t n ) Δ z n i + d g i ( t n ) d t ( Δ w n i h n − Δ z n i ) ) , ( 7.3 ) {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r} +\sum \limits _{i=1}^{m}\left(\mathbf {g} _{i}(t_{n})\Delta \mathbf {w} _{n}^{i}\mathbf {f} _{\mathbf {x} }(t_{n},{\widetilde {\mathbf {y} }}_{n})\mathbf {g} _{i}(t_{n})\Delta \mathbf {z} _{n}^{i}+{\frac {d\mathbf {g} _{i}(t_{n})}{dt}}(\Delta \mathbf {w} _{n}^{i}h_{n}-\Delta \mathbf {z} _{n}^{i})\right),\qquad \qquad (7.3)}
где матрицы M n {\displaystyle \mathbf {M} _{n}} L {\displaystyle \mathbf {L} } r {\displaystyle \mathbf {r} }
M n = [ f x ( t n , y n ) f t ( t n , y n ) + 1 2 ∑ j = 1 m ( I ⊗ g j ⊺ ( t n ) ) f x x ( t n , y n ) g j ( t n ) f ( t n , y n ) 0 0 1 0 0 0 ] ∈ R ( d + 2 ) × ( d + 2 ) , {\displaystyle \mathbf {M} _{n}={\begin{bmatrix}\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {y} _{n})&\mathbf {f} _{t}(t_{n},\mathbf {y} _{n})+{\frac {1}{2}}\sum \limits _{j=1}^{m}\left(\mathbf {I} \otimes \mathbf {g} _{j}^{\intercal }(t_{n})\right)\mathbf {f} _{\mathbf {xx} }(t_{n},\mathbf {y} _{n})\mathbf {g} _{j}(t_{n})&\mathbf {f} (t_{n},\mathbf {y} _{n})\\0&0&1\\0&0&0\end{bmatrix}}\in \mathbb {R} ^{(d+2)\times (d+2)},}
L = [ I 0 d × 2 ] , r ⊺ = [ 0 1 × ( d + 1 ) 1 ] {\displaystyle \mathbf {L} =\left[{\begin{array}{ll}\mathbf {I} &\mathbf {0} _{d\times 2}\end{array}}\right],\mathbf {r} ^{\intercal }=\left[{\begin{array}{ll}\mathbf {0} _{1\times (d+1)}&1\end{array}}\right]} Δ z n i {\displaystyle \Delta \mathbf {z} _{n}^{i}} E ( ( Δ z n i ) 2 ) = 1 3 h n 3 {\displaystyle E\left((\Delta \mathbf {z} _{n}^{i})^{2}\right)={\frac {1}{3}}h_{n}^{3}} E ( Δ w n i Δ z n i ) = 1 2 h n 2 {\displaystyle E(\Delta \mathbf {w} _{n}^{i}\Delta \mathbf {z} _{n}^{i})={\frac {1}{2}}h_{n}^{2}} p+q>1 [12] . Для больших систем СДУ [12] ( P p , q ( 2 − k n M n h n ) ) 2 k n r {\displaystyle (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r} } k m n , k n p , q ( h n , M n , r ) {\displaystyle \mathbf {\mathbf {k} } _{m_{n},k_{n}}^{p,q}(h_{n},\mathbf {M} _{n},\mathbf {r} )}
Заказать 2 схемы SLL-Тейлора [ править ] y t n + 1 = y n + L ( P p , q ( 2 − k n M n h n ) ) 2 k n r + ∑ j = 1 m g j ( t n ) Δ w n j + ∑ j = 1 m f x ( t n , y n ) g j ( t n ) J ~ ( j , 0 ) + ∑ j = 1 m d g j d t ( t n ) J ~ ( 0 , j ) {\displaystyle \mathbf {y} _{t_{n+1}}=\mathbf {y} _{n}+\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r} +\sum \limits _{j=1}^{m}\mathbf {g} _{j}\left(t_{n}\right)\Delta \mathbf {w} _{n}^{j}+\sum \limits _{j=1}^{m}\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {y} _{n})\mathbf {g} _{j}\left(t_{n}\right){\widetilde {J}}_{\left(j,0\right)}+\sum \limits _{j=1}^{m}{\frac {d\mathbf {g} _{_{j}}}{dt}}\left(t_{n}\right){\widetilde {J}}_{\left(0,j\right)}}
+ ∑ j 1 , j 2 = 1 m ( I ⊗ g j 2 ⊺ ( t n ) ) f x x ( t n , y n ) g j 1 ( t n ) J ~ ( j 1 , j 2 , 0 ) , ( 7.4 ) {\displaystyle \qquad \qquad +\sum \limits _{j_{1},j_{2}=1}^{m}\left(\mathbf {I} \otimes \mathbf {g} _{j_{2}}^{\intercal }\left(t_{n}\right)\right)\mathbf {f} _{\mathbf {xx} }(t_{n},\mathbf {y} _{n})\mathbf {g} _{j_{1}}\left(t_{n}\right){\widetilde {J}}_{\left(j_{1},j_{2},0\right),}\qquad \qquad (7.4)}
где M n {\displaystyle \mathbf {M} _{n}} L {\displaystyle \mathbf {L} } r {\displaystyle \mathbf {r} } Δ w n i {\displaystyle \Delta \mathbf {w} _{n}^{i}} J ~ α {\displaystyle {\widetilde {J}}_{\alpha }} приближением второго порядка кратного интеграла Стратонова J α {\displaystyle J_{\alpha }} [20]
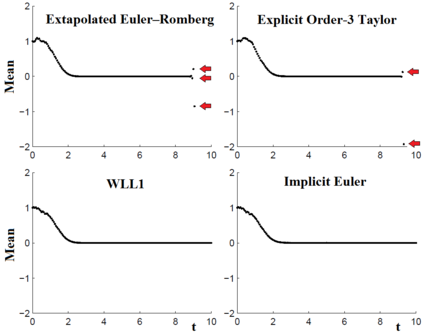
Заказать 2 схемы СЛЛ-РК [ править ] Рис. 4, вверху : Эволюция областей на фазовой плоскости гармонического осциллятора (7.6) при ε=0 и ω=σ=1. Изображения исходного единичного круга (зеленый) получены в три момента времени T по точному решению (черный) и по схемам SLL1 (синий) и Неявный Эйлер (красный) с h=0,05 . Внизу : ожидаемое значение энергии (сплошная линия) вдоль решения нелинейного осциллятора (7.6) с ε=1 и ω=100 и его аппроксимация (кружки), вычисленная методом Монте-Карло с помощью 10 000 симуляций схемы SLL1 с h. =1/2 и p=q=6 . Для СДУ с одним винеровским шумом (m=1 ) [20]
y t n + 1 = y n + ϕ ~ ( t n , y n ; h n ) + h n 2 ( k 1 + k 2 ) + g ( t n ) Δ w n + ( g ( t n + 1 ) − g ( t n ) ) h n J ( 0 , 1 ) ( 7.5 ) {\displaystyle \mathbf {y} _{t_{n+1}}=\mathbf {y} _{n}+{\widetilde {\mathbf {\phi } }}(t_{n},\mathbf {y} _{n};h_{n})+{\frac {h_{n}}{2}}\left(\mathbf {k} _{1}+\mathbf {k} _{2}\right)+\mathbf {g} \left(t_{n}\right)\Delta w_{n}+{\frac {\left(\mathbf {g} \left(t_{n+1}\right)-\mathbf {g} \left(t_{n}\right)\right)}{h_{n}}}J_{\left(0,1\right)}\quad (7.5)}
{\displaystyle \quad \quad \quad }
где
k 1 = f ( t n + h n 2 , y n + ϕ ~ ( t n , y n ; h n 2 ) + γ + ) − f x ( t n , y n ) ϕ ~ ( t n , y n ; h n 2 ) − f ( t n , y n ) − f t ( t n , y n ) h n 2 , {\displaystyle \mathbf {k} _{1}=\mathbf {f} (t_{n}+{\frac {h_{n}}{2}},\mathbf {y} _{n}+{\widetilde {\mathbf {\phi } }}(t_{n},\mathbf {y} _{n};{\frac {h_{n}}{2}})+\gamma _{+})-\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {y} _{n}){\widetilde {\mathbf {\phi } }}(t_{n},\mathbf {y} _{n};{\frac {h_{n}}{2}})-\mathbf {f} \left(t_{n},\mathbf {y} _{n}\right)-\mathbf {f} _{t}\left(t_{n},\mathbf {y} _{n}\right){\frac {h_{n}}{2}},} k 2 = f ( t n + h n 2 , y n + ϕ ~ ( t n , y n ; h n 2 ) + γ − ) − f x ( t n , y n ) ϕ ~ ( t n , y n ; h n 2 ) − f ( t n , y n ) − f t ( t n , y n ) h n 2 , {\displaystyle \mathbf {k} _{2}=\mathbf {f} (t_{n}+{\frac {h_{n}}{2}},\mathbf {y} _{n}+{\widetilde {\mathbf {\phi } }}(t_{n},\mathbf {y} _{n};{\frac {h_{n}}{2}})+\gamma _{-})-\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {y} _{n}){\widetilde {\mathbf {\phi } }}(t_{n},\mathbf {y} _{n};{\frac {h_{n}}{2}})-\mathbf {f} \left(t_{n},\mathbf {y} _{n}\right)-\mathbf {f} _{t}\left(t_{n},\mathbf {y} _{n}\right){\frac {h_{n}}{2}},} с γ ± = 1 h n g ( t n ) ( J ~ ( 1 , 0 ) ± 2 J ~ ( 1 , 1 , 0 ) h n − J ~ ( 1 , 0 ) 2 ) {\displaystyle \gamma _{\pm }={\frac {1}{h_{n}}}\mathbf {g} \left(t_{n}\right){\Bigl (}{\widetilde {J}}_{\left(1,0\right)}\pm {\sqrt {2{\widetilde {J}}_{\left(1,1,0\right)}h_{n}-{\widetilde {J}}_{\left(1,0\right)}^{2}}}{\Bigr )}}
Здесь, ϕ ~ ( t n , y n ; h n ) = L ( P p , q ( 2 − k n M n h n ) ) 2 k n r {\displaystyle {\widetilde {\mathbf {\phi } }}(t_{n},\mathbf {y} _{n};h_{n})=\mathbf {L} (\mathbf {P} _{p,q}(2^{-k_{n}}\mathbf {M} _{n}h_{n}))^{2^{k_{n}}}\mathbf {r} } ϕ ~ ( t n , y n ; h n ) = L k m n , k n p , q ( h n , M n , r ) {\displaystyle {\widetilde {\mathbf {\phi } }}(t_{n},\mathbf {y} _{n};h_{n})=\mathbf {L\mathbf {k} } _{m_{n},k_{n}}^{p,q}(h_{n},\mathbf {M} _{n},\mathbf {r} )} M n {\displaystyle \mathbf {M} _{n}} L {\displaystyle \mathbf {L} } r {\displaystyle \mathbf {r} } Δ w n i {\displaystyle \Delta \mathbf {w} _{n}^{i}} J ~ α {\displaystyle {\widetilde {J}}_{\alpha }} 2 , p+q>1 и m n > 2 {\displaystyle m_{n}>2}
Стабильность и динамика [ править ] По построению сильные дискретизации LL и HOLL наследуют устойчивость и динамику линейных СДУ, но это не относится к сильным схемам LL в целом. схемы ЛЛ (7.2)-(7.5) с p ≤ q ≤ p + 2 {\displaystyle p\leq q\leq p+2} A -стабильными, включая жесткие и высококолебательные линейные уравнения. [12] случайными аттракторами эти схемы также имеют случайный аттрактор, сходящийся по вероятности к точному при уменьшении размера шага и сохраняющий эргодичность этих уравнений для любого размера шага. [20] [12] [20] [22] g i ( t ) ≈ 0 {\displaystyle \mathbf {g} _{i}(t)\approx 0} [20]
d x ( t ) = y ( t ) d t , x 1 ( 0 ) = 0.01 d y ( t ) = − ( ω 2 x ( t ) + ϵ x 4 ( t ) ) d t + σ d w t , x 1 ( 0 ) = 0.1 , ( 7.6 ) {\displaystyle {\begin{array}{ll}dx(t)=y(t)dt,&x_{1}(0)=0.01\\dy(t)=-(\omega ^{2}x(t)+\epsilon x^{4}(t))dt+\sigma dw_{t},&x_{1}(0)=0.1,\end{array}}\qquad \qquad (7.6)}
и их аппроксимации двумя численными схемами.
методы LL SDE Слабые для Рассмотрим d -мерное стохастическое дифференциальное уравнение
d x ( t ) = f ( t , x ( t ) ) d t + ∑ i = 1 m g i ( t ) d w i ( t ) , t ∈ [ t 0 , T ] , ( 8.1 ) {\displaystyle d\mathbf {x} (t)=\mathbf {f} (t,\mathbf {x} (t))dt+\sum \limits _{i=1}^{m}\mathbf {g} _{i}(t)d\mathbf {w} ^{i}(t),\qquad t\in \left[t_{0},T\right],\qquad \qquad (8.1)}
с начальным состоянием x ( t 0 ) = x 0 {\displaystyle \mathbf {x} (t_{0})=\mathbf {x} _{0}} f {\displaystyle \mathbf {f} } g i {\displaystyle \mathbf {g} _{i}} w = ( w 1 , … , w m ) {\displaystyle \mathbf {w=(\mathbf {w} } ^{1},\ldots ,\mathbf {w} ^{m}\mathbf {)} } m -мерный стандартный винеровский процесс.
Локальная дискретизация линейная Для временной дискретизации ( t ) h {\displaystyle \left(t\right)_{h}} β {\displaystyle \mathbb {\beta } } ( = 1 , 2 ) {\displaystyle (=1,2)} Слабая локальная линейная дискретизация решения СДУ (8.1) определяется рекурсивным соотношением [23]
z n + 1 = z n + ϕ β ( t n , z n ; h n ) + η ( t n , z n ; h n ) , w i t h z 0 = x 0 , {\displaystyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } _{\mathbb {\beta } }(t_{n},\mathbf {z} _{n};h_{n})+\mathbf {\eta } (t_{n},\mathbf {z} _{n};h_{n}),\quad with\quad \mathbf {z} _{0}=\mathbf {x} _{0},}
где
ϕ β ( t n , z n ; δ ) = ∫ 0 δ e f x ( t n , z n ) ( δ − u ) ( f ( t n , z n ) + b β ( t n , z n ) u ) d u {\displaystyle \mathbf {\phi } _{\mathbb {\beta } }(t_{n},\mathbf {z} _{n};\delta )=\int _{0}^{\delta }e^{\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})(\delta -u)}(\mathbf {f(} t_{n},\mathbf {z} _{n})+\mathbf {b} ^{\mathbb {\beta } }(t_{n},\mathbf {z} _{n})u)du}
с
b β ( t n , z n ) = { f t ( t n , z n ) for β = 1 f t ( t n , z n ) + 1 2 ∑ j = 1 m ( I ⊗ g j ⊺ ( t n ) ) f x x ( t n , z n ) g j ( t n ) for β = 2 , {\displaystyle \mathbf {b} ^{\mathbb {\beta } }(t_{n},\mathbf {z} _{n})={\begin{cases}\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})&{\text{for }}\mathbb {\beta } =1\\\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})+{\frac {1}{2}}\sum \limits _{j=1}^{m}\left(\mathbf {I} \otimes \mathbf {g} _{j}^{\intercal }\left(t_{n}\right)\right)\mathbf {f} _{\mathbf {xx} }(t_{n},\mathbf {z} _{n})\mathbf {g} _{j}\left(t_{n}\right)&{\text{for }}\mathbb {\beta } =2,\end{cases}}}
и η ( t n , z n ; δ ) {\displaystyle \mathbf {\eta } (t_{n},\mathbf {z} _{n};\delta )}
Σ ( t n , z n ; δ ) = ∫ 0 δ e f x ( t n , z n ) ( δ − s ) G ( t n + s ) G ⊺ ( t n + s ) e f x ⊺ ( t n , z n ) ( δ − s ) d s . {\displaystyle \mathbf {\Sigma } (t_{n},\mathbf {z} _{n};\delta )=\int \limits _{0}^{\delta }e^{\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})(\delta -s)}\mathbf {G} (t_{n}+s)\mathbf {G} ^{\intercal }(t_{n}+s)e^{\mathbf {f} _{\mathbf {x} }^{\intercal }(t_{n},\mathbf {z} _{n})(\delta -s)}ds.}
Здесь, f x {\displaystyle \mathbf {f} _{\mathbf {x} }} f t {\displaystyle \mathbf {f} _{t}} f {\displaystyle \mathbf {f} } x {\displaystyle \mathbf {x} } t соответственно f x x {\displaystyle \mathbf {f} _{\mathbf {xx} }} f {\displaystyle \mathbf {f} } x {\displaystyle \mathbf {x} } G ( t ) = [ g 1 ( t ) , … , g m ( t ) ] {\displaystyle \mathbf {G} (t)=[\mathbf {g} _{1}(t),\ldots ,\mathbf {g} _{m}(t)]} z n + 1 {\displaystyle \mathbf {z} _{n+1}} сходится с порядком β {\displaystyle \mathbb {\beta } }
Схемы локальной линеаризации [ править ] В зависимости от способа расчета ϕ β {\displaystyle \mathbf {\phi } _{\mathbb {\beta } }} Σ {\displaystyle \mathbf {\Sigma } } y n {\displaystyle \mathbf {y} _{n}} z n {\displaystyle \mathbf {z} _{n}} схемой слабой локальной линеаризации (WLL) .
Схема WLL заказа 1 [ править ] y n + 1 = y n + B 14 + ( B 12 B 11 ⊺ ) 1 / 2 ξ n {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {B} _{14}+(\mathbf {B} _{12}\mathbf {B} _{11}^{\intercal })^{1/2}\mathbf {\xi } _{n}} [24] [25]
где для СДУ с автономными коэффициентами диффузии B 11 {\displaystyle \mathbf {B} _{11}} B 12 {\displaystyle \mathbf {B} _{12}} B 14 {\displaystyle \mathbf {B} _{14}} разделенной матрицей B = P p , q ( 2 − k n M n h n ) ) 2 k n {\displaystyle \mathbf {B} =\mathbf {P} _{p,q}(2^{-k_{n}}{\mathcal {M}}_{n}h_{n}))^{2^{k_{n}}}}
M n = [ f x ( t n , y n ) G G ⊺ f t ( t n , y n ) f ( t n , y n ) 0 − f x ⊺ ( t n , y n ) 0 0 0 0 0 1 0 0 0 0 ] ∈ R ( 2 d + 2 ) × ( 2 d + 2 ) , {\displaystyle {\mathcal {M}}_{n}=\left[{\begin{array}{cccc}\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {y} _{n})&\mathbf {GG} ^{\intercal }&\mathbf {f} _{t}(t_{n},\mathbf {y} _{n})&\mathbf {f} (t_{n},\mathbf {y} _{n})\\\mathbf {0} &-\mathbf {f} _{\mathbf {x} }^{\intercal }(t_{n},\mathbf {y} _{n})&\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &0&1\\\mathbf {0} &\mathbf {0} &0&0\end{array}}\right]\in \mathbb {R} ^{(2d+2)\times (2d+2)},}
и { ξ n } {\displaystyle \{\mathbf {\xi } _{n}\}} d -мерных независимых двухточечных распределенных случайных векторов, удовлетворяющих P ( ξ n k = ± 1 ) = 1 2 {\displaystyle P(\xi _{n}^{k}=\pm 1)={\frac {1}{2}}}
Схема WLL заказа 2 [ править ] y n + 1 = y n + B 16 + ( B 14 B 11 ⊺ ) 1 / 2 ξ n , {\displaystyle \mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {B} _{16}+(\mathbf {B} _{14}\mathbf {B} _{11}^{\intercal })^{1/2}\mathbf {\xi } _{n},} [24] [25]
где B 11 {\displaystyle \mathbf {B} _{11}} B 14 {\displaystyle \mathbf {B} _{14}} B 16 {\displaystyle \mathbf {B} _{16}} B = P p , q ( 2 − k n M n h n ) ) 2 k n {\displaystyle \mathbf {B} =\mathbf {P} _{p,q}(2^{-k_{n}}{\mathcal {M}}_{n}h_{n}))^{2^{k_{n}}}}
M n = [ J H 2 H 1 H 0 a 2 a 1 0 − J ⊺ I 0 0 0 0 0 − J ⊺ I 0 0 0 0 0 − J ⊺ 0 0 0 0 0 0 0 1 0 0 0 0 0 0 ] ∈ R ( 4 d + 2 ) × ( 4 d + 2 ) , {\displaystyle {\mathcal {M}}_{n}=\left[{\begin{array}{cccccc}\mathbf {J} &\mathbf {H} _{2}&\mathbf {H} _{1}&\mathbf {H} _{0}&\mathbf {a} _{2}&\mathbf {a} _{1}\\\mathbf {0} &-\mathbf {J} ^{\intercal }&\mathbf {I} &\mathbf {0} &\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &-\mathbf {J} ^{\intercal }&\mathbf {I} &\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &\mathbf {0} &-\mathbf {J} ^{\intercal }&\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &\mathbf {0} &\mathbf {0} &0&1\\\mathbf {0} &\mathbf {0} &\mathbf {0} &\mathbf {0} &0&0\end{array}}\right]\in \mathbb {R} ^{(4d+2)\times (4d+2)},}
J = f x ( t n , y n ) a 1 = f ( t n , y n ) a 2 = f t ( t n , y n ) + 1 2 ∑ i = 1 m ( I ⊗ ( g i ( t n ) ) ⊺ ) f x x ( t n , y n ) g i ( t n ) {\displaystyle \mathbf {J} =\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {y} _{n})\qquad \mathbf {a} _{1}=\mathbf {f} (t_{n},\mathbf {y} _{n})\qquad \mathbf {a} _{2}=\mathbf {f} _{t}(t_{n},\mathbf {y} _{n})+{\frac {1}{2}}\sum \limits _{i=1}^{m}(\mathbf {I} \otimes (\mathbf {g} ^{i}(t_{n}))^{\intercal })\mathbf {f} _{\mathbf {xx} }(t_{n},\mathbf {y} _{n})\mathbf {g} ^{i}(t_{n})}
и
H 0 = G ( t n ) G ⊺ ( t n ) H 1 = G ( t n ) d G ⊺ ( t n ) d t + d G ( t n ) d t G ⊺ ( t n ) H 2 = d G ( t n ) d t d G ⊺ ( t n ) d t . {\displaystyle \mathbf {H} _{0}=\mathbf {G} (t_{n})\mathbf {G} ^{\intercal }(t_{n})\qquad \mathbf {H} _{1}=\mathbf {G} (t_{n}){\frac {d\mathbf {G} ^{\intercal }(t_{n})}{dt}}+{\frac {d\mathbf {G} (t_{n})}{dt}}\mathbf {G} ^{\intercal }(t_{n})\qquad \mathbf {H} _{2}={\frac {d\mathbf {G} (t_{n})}{dt}}{\frac {d\mathbf {G} ^{\intercal }(t_{n})}{dt}}{\text{.}}}
Стабильность и динамика [ править ] Рис. 5. 100 симуляциях различных схем с h=1/16 и p=q=6 . По построению слабые LL-дискретизации наследуют устойчивость и динамику линейных СДУ, но это не относится к слабым LL-схемам в целом. Схемы WLL, с p ≤ q ≤ p + 2 , {\displaystyle p\leq q\leq p+2,} первые два момента линейных СДУ и наследует среднеквадратическую устойчивость или нестабильность, которую может иметь такое решение. [24] эргодичность линейных уравнений и являются геометрически эргодическими для некоторых классов нелинейных СДУ. [26] g i ( t ) ≈ 0 {\displaystyle \mathbf {g} _{i}(t)\approx 0} [24]
d x = − t 2 x d t + 3 2 ( t + 1 ) e − t 3 / 3 d w t , x ( 0 ) = 1 , ( 8.2 ) {\displaystyle dx=-t^{2}x{\text{ }}dt+{\frac {3}{2(t+1)}}e^{-t^{3}/3}{\text{ }}dw_{t},\qquad \qquad x(0)=1,\qquad \quad (8.2)}
рассчитывается по различным схемам.
Исторические заметки [ править ] Ниже представлена временная шкала основных разработок метода локальной линеаризации (LL).
Поуп Д.А. (1963) представляет дискретизацию LL для ОДУ и схему LL, основанную на расширении Тейлора. [2] Озаки Т. (1985) представляет метод LL для интегрирования и оценки СДУ. Термин «локальная линеаризация» используется впервые. [27] Бискай Р. и др. (1996) переформулировали сильный метод ЛЛ для СДУ. [19] Сёдзи И. и Озаки Т. (1997) переформулируют слабый метод LL для СДУ. [23] Хохбрук М. и др. (1998) представили схему LL для ОДУ, основанную на аппроксимации подпространств Крылова. [3] Хименес Х.К. (2002) представляет схему LL для ОДУ и СДУ, основанную на рациональной аппроксимации Паде. [21] Карбонелл FM и др. (2005) представили метод LL для RDE. [16] Хименес Дж.С. и др. (2006) представили метод LL для DDE. [11] Де ла Круз Х. и др. (2006, 2007) и Токман М. (2006) представляют два класса интеграторов HOLL для ОДУ: основанные на интеграторах [6] [7] [5] Де ла Круз Х. и др. (2010) представили сильный метод ХОЛЛА для СДУ. [20] ^ Jump up to: Перейти обратно: а б с д Хименес Х.К. (2009). «Методы локальной линеаризации для численного интегрирования обыкновенных дифференциальных уравнений: обзор». Технический отчет ICTP . 035: 357–373. ^ Jump up to: Перейти обратно: а б Поуп, Д.А. (1963). «Экспоненциальный метод численного интегрирования обыкновенных дифференциальных уравнений». Комм. АКМ, 6 (8), 491–493. дои: 10.1145/366707.367592 . ^ Jump up to: Перейти обратно: а б с Хохбрук М., Любич К. и Сельхофер Х. (1998). «Экспоненциальные интеграторы для больших систем дифференциальных уравнений». СИАМ Дж. Сайент. Вычислить. 19 (5), 1552–1574. дои:10.1137/S1064827595295337 . ^ Jump up to: Перейти обратно: а б с д и ж г час де ла Крус Х.; Бискайский Р.Дж.; Хименес Х.К.; Карбонелл Ф. (2013). «Локальная линеаризация - методы Рунге Кутты: класс A-стабильных явных интеграторов для динамических систем». Математика. Вычислить. Моделирование. 57 (3–4): 720–740. doi:10.1016/j.mcm.2012.08.011 . ^ Jump up to: Перейти обратно: а б с д и ж г час де ла Крус Х.; Бискайский Р.Дж.; Карбонелл Ф.; Одзаки Т.; Хименес Х.К. (2007). «Метод локальной линеаризации более высокого порядка для решения обыкновенных дифференциальных уравнений». Прил. Математика. Вычислить. 185: 197–212. doi:10.1016/j.amc.2006.06.096 . ^ Jump up to: Перейти обратно: а б с д и де ла Крус Х.; Бискайский Р.Дж.; Карбонелл Ф.; Хименес Х.К.; Одзаки Т. (2006). «Методы локальной линеаризации-Рунге-Кутты (LLRK) для решения обыкновенных дифференциальных уравнений». Конспект лекций по информатике 3991: 132–139, Springer-Verlag. дои:10.1007/11758501_22 . ISBN 978-3-540-34379-0 . ^ Jump up to: Перейти обратно: а б Токман М. (2006). «Эффективная интеграция больших жестких систем ОДУ с итерационными методами экспоненциального распространения (EPI)». Дж. Компьютер. Физика. 213 (2): 748–776. doi:10.1016/j.jcp.2005.08.032 . ^ М. Хохбрук.; А. Остерманн. (2011). «Экспоненциальные многошаговые методы типа Адамса». БИТ Число. Математика. 51 (4): 889–908. doi:10.1007/s10543-011-0332-6 . ^ Jump up to: Перейти обратно: а б с д и Хименес, Дж. К., и Карбонелл, Ф. (2005). «Скорость сходимости схем локальной линеаризации начальных задач». Прил. Математика. Компьютер., 171(2), 1282–1295. doi:10.1016/j.amc.2005.01.118 . ^ Карбонелл Ф.; Хименес Х.К.; Педросо Л.М. (2008). «Вычисление кратных интегралов с использованием матричных экспонент». Дж. Компьютер. Прил. Математика. 213: 300–305. doi:10.1016/j.cam.2007.01.007 . ^ Jump up to: Перейти обратно: а б с д Хименес Х.К.; Педросо Л.; Карбонелл Ф.; Эрнандес В. (2006). «Метод локальной линеаризации численного интегрирования дифференциальных уравнений с запаздыванием». СИАМ Дж. Нумер. Анализ. 44 (6): 2584–2609. дои: 10.1137/040607356 . ^ Jump up to: Перейти обратно: а б с д и ж Хименес Х.К.; де ла Крус Х. (2012). «Скорость сходимости схем сильной локальной линеаризации стохастических дифференциальных уравнений с аддитивным шумом». БИТ Число. Математика. 52 (2): 357–382. doi:10.1007/s10543-011-0360-2 . ^ Jump up to: Перейти обратно: а б с Хименес Х.К.; Бискайский Р.; Мора С.; Родригес Л.М. (2002). «Динамические свойства метода локальной линеаризации для начальных задач». Прил. Математика. Вычислить. 126: 63–68. doi:10.1016/S0096-3003(00)00100-4 . ^ Хименес Дж.К.; Сотолонго А.; Санчес-Борно Ж.М. (2014). «Локально линеаризованный метод Рунге Кутты Дормана и Принца». Прил. Математика. Вычислить. 247: 589–606. doi:10.1016/j.amc.2014.09.001 . ^ Наранхо-Нода, Хименес Х.К. (2021) «Локально линеаризованный метод Рунге_Кутты Дормана и Принца для больших систем задач начального значения». Дж.Компьютер. Физика. 426: 109946. doi:10.1016/j.jcp.2020.109946 . ^ Jump up to: Перейти обратно: а б с Карбонелл Ф., Хименес Дж. К., Бискай Р. Дж. и Де Ла Круз Х. (2005). «Метод локальной линеаризации численного интегрирования случайных дифференциальных уравнений». БИТ Номер. Математика. 45(1), 1-14. doi:10.1007/S10543-005-2645-9 . ^ Jump up to: Перейти обратно: а б Хименес Х.К.; Карбонелл Ф. (2009). «Скорость сходимости схем локальной линеаризации случайных дифференциальных уравнений». БИТ Число. Математика. 49 (2): 357–373. doi:10.1007/s10543-009-0225-0 . ^ Хименес Х.К., Сёдзи И., Озаки Т. (1999) «Моделирование стохастического дифференциального уравнения с помощью метода локальной линеаризации. Сравнительное исследование». Дж. Статист. Физика. 99: 587-602, дои: 10.1023/А: 1004504506041 . ^ Jump up to: Перейти обратно: а б Бискай, Р., Хименес, Дж. К., Риера, Дж. Дж., и Вальдес, Пенсильвания (1996). «Метод локальной линеаризации численного решения стохастических дифференциальных уравнений». Анналы Инст. Статис. Математика. 48(4), 631-644. дои:10.1007/BF00052324 . ^ Jump up to: Перейти обратно: а б с д и ж г де ла Крус Х.; Бискайский Р.Дж.; Хименес Х.К.; Карбонелл Ф.; Одзаки Т. (2010). «Методы локальной линеаризации высокого порядка: подход к построению A-стабильных явных схем высокого порядка для стохастических дифференциальных уравнений с аддитивным шумом». БИТ Число. Математика. 50 (3): 509–539. doi:10.1007/s10543-010-0272-6 . ^ Jump up to: Перейти обратно: а б с Хименес, JC (2002). «Простое алгебраическое выражение для оценки схем локальной линеаризации стохастических дифференциальных уравнений». Прил. Математика. Письма, 15 (6), 775–780. doi:10.1016/S0893-9659(02)00041-1 . ^ де ла Крус Х.; Хименес Х.К.; Зубелли Дж. П. (2017). «Локально линеаризованные методы моделирования стохастических осцилляторов, управляемых случайными силами». БИТ Число. Математика. 57: 123–151. doi:10.1007/s10543-016-0620-2 . ^ Jump up to: Перейти обратно: а б Сёдзи И. и Одзаки Т. (1997). «Сравнительное исследование методов оценки непрерывных во времени случайных процессов». Дж. Анал временных рядов. 18(5), 485-506. дои: 10.1111/1467-9892.00064 . ^ Jump up to: Перейти обратно: а б с д Хименес Х.К.; Карбонелл Ф. (2015). «Скорость сходимости слабых схем локальной линеаризации стохастических дифференциальных уравнений с аддитивным шумом». Дж. Компьютер. Прил. Математика. 279: 106–122. doi:10.1016/j.cam.2014.10.021 . ^ Jump up to: Перейти обратно: а б Карбонелл Ф.; Хименес Х.К.; Бискайский Р.Дж. (2006). «Слабая локальная линейная дискретизация стохастических дифференциальных уравнений: сходимость и численные схемы». Дж. Компьютер. Прил. Математика. 197: 578–596. doi:10.1016/j.cam.2005.11.032 . ^ Хансен Н.Р. (2003) «Геометрическая эргодичность приближений дискретного времени к многомерной диффузии». Бернулли. 9: 725-743, doi:10.3150/bj/1066223276 . ^ Одзаки, Т. (1985). «Нелинейные модели временных рядов и динамические системы». Справочник по статистике, 5, 25-83. doi:10.1016/S0169-7161(85)05004-0 . 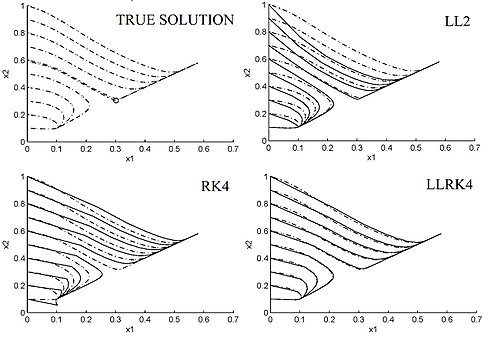



![{\displaystyle {\frac {d\mathbf {x} \left(t\right)}{dt}}=\mathbf {f} \left(t,\mathbf {x} \left(t\right)\right ),\qquad t\in \left[t_{0},T\right],\qquad \qquad \qquad \qquad (4.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b689077ae401751f25375eb3338ed66cc57f756a)



![{\displaystyle [t_{0},T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/986ba7ea2bc36ce31beb5c5f4faffbfb6405f69b)



















![{\displaystyle т\in \lbrack t_{k},t_{k+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dacd0fb31482f9ac95b8c3261d9dc00f1055dca4)


![{\displaystyle \mathbf {c} =\left[c_{i}\right],\mathbf {A} =\left[a_{ij}\right]\quad and\quad \mathbf {b} =\left[ б_{j}\вправо]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fbc317004aaf306e62ecc1c6d08e4f49d9d0543)

















![{\displaystyle \mathbf {L} =[\mathbf {I} \quad \mathbf {0} _ {d\times l}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75b8ac2636b6ebd86e0bba8f06886336cfc6ec82)
![{\displaystyle \mathbf {r} =[\mathbf {0} _{1\times (d+l-1)}\quad 1]^{\intercal },}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3710227203d25399ba90fb8e8f94a9d34ff29aa9)














![{\displaystyle \mathbf {L} =\left[{\begin{array}{ll}\mathbf {I} &\mathbf {0} _{d\times 2}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05d54f18477ecdb4b717abf25a75b96d17729bcd)
![{\displaystyle\mathbf{r}^{\intercal}=\left[{\begin{array}{ll}\mathbf{0}_{1\times(d+1)}&1\end{array}}\ верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f82230fb66e66705351377690e9f14c8d4a41224)






![{\displaystyle\mathbf{T}_{n}=\left[{\begin{array}{cccc}\mathbf{f}_{\mathbf{x}}(\mathbf{y}_{n})& (\mathbf{I}\otimes\mathbf{f}^{\intercal}(\mathbf{y}_{n}))\mathbf{f}_{\mathbf{xx}}(\mathbf{y}_ {n})\mathbf{f}(\mathbf{y}_{n})&\mathbf{0}&\mathbf{f}(\mathbf{y}_{n})\\0&0&0&0\\0&0&0&1\ \0&0&0&0\end{array}}\right]\in\mathbb{R}^{(d+3)\times(d+3)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04b4535597fcece8be4c40e7b4ae75229d8f9831)
![{\displaystyle\mathbf{L}_{1}=\left[{\begin{array}{ll}\mathbf{I} &\mathbf{0}_{d\times3}\end{array}}\ right ]\quad and\quad\mathbf{r}_{1}^{\intercal}=\left[{\begin{array}{ll}\mathbf{0}_{1\times(d+2)} &1 \end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f495cb0102ab17316c499936bd236cdb35f4ebbd)






![{\displaystyle\mathbf{k}_{1}\equiv\mathbf{0},c=\left[{\begin{array}{cccc}0&{\frac {1}{2}}&{\frac { 1}{2}}&1\end{array}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c7569810b131c3d8e9ad24b6201f9454d90fbbc)










![{\displaystyle {\begin{aligned}&{\frac {dx_{1}}{dt}}=-2x_{1}+x_{2}+1-\mu f(x_{1},\lambda)\ qquad \qquad (4.10)\\[6pt]&{\frac {dx_{2}}{dt}}=x_{1}-2x_{2}+1-\mu f(x_{2},\lambda ) \qquad \qquad \quad (4.11)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/855ec9f888ae9f2a03221800414cbf76ef9edd46)




![{\displaystyle {\frac {d\mathbf {x} (t)}{dt}}=\mathbf {f} (t,\mathbf {x} (t),\mathbf {x} _{t}(- \tau _{1}),\ldots ,\mathbf {x} _{t}(-\tau _{m})),\qquad t\in [t_{0},T],\qquad \qquad ( 5.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/682b3725e57d7e2ee5324a0a139b7e2d1063767b)


![{\displaystyle s\in [-\tau,0],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e9d0232ea2938ec04dafc8665c88403f10670c3)
![{\displaystyle \mathbf {x} _{t}:[-\tau,0]\longrightarrow \mathbb {R} ^{d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026aa256631bc0e92437d8cea3a76cd0c6c2aded)
![{\displaystyle \mathbf {x} _{t}(s):=\mathbf {x} (t+s),{\text{ }}s\in [-\tau,0],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/857fd392ec867a13d23dcb2ea2d705d132a706d6)
![{\displaystyle t\in [t_{0},T],\mathbf {\varphi} :[-\tau,0]\longrightarrow \mathbb {R} ^{d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/332fbe38ea2b9aa1ca97db545170bba5e188883f)



![{\displaystyle \Phi (t_{n},\mathbf {z}_{n},h_{n};{\widetilde {\mathbf {z} }}_{t_{n}}^{1},\ ldots ,{\widetilde {\mathbf {z} }}_{t_{n}}^{m})=\int \limits _{0}^{h_{n}}e^{\mathbf {A}_ {n}(h_{n}-u)}\left[\sum \limits _{i=1}^{m}\mathbf {B}_{n}^{i}({\widetilde {\mathbf { z} }}_{t_{n}}^{i}(u-\tau _{i})-{\widetilde {\mathbf {z} }}_{t_{n}}^{i}(- \tau _{i}))+\mathbf {d}_{n}\right]\,du+\int \limits _{0}^{h_{n}}\int \limits _{0}^{u }e^{\mathbf {A}_{n}(h_{n}-u)}\mathbf {c}_{n}\,dr\,du}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d522057eb0209091646bcc9221b24d9e13d0e371)
![{\displaystyle {\widetilde {\mathbf {z}}}_{t_{n}}^{i}:\left[-\tau _{i},0\right]\longrightarrow \mathbb {R} ^{ д}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3f4bc0cc5b10a10d0844d2265aababd5028d6e4)
![{\displaystyle {\widetilde {\mathbf {z} }}_{t_{n}}^{i}(s):= {\widetilde {\mathbf {z} }}^{i}(t_{n} +s),{\text{ }}s\in [-\tau _{i},0],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4c1d308208faf6bc44261b2ce1b128a9f394195)
![{\displaystyle {\widetilde {\mathbf {z}}}^{i}:\left[t_{n}-\tau _{i},t_{n}\right]\longrightarrow \mathbb {R} ^{ д}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/922ac10d7369b3ff0ffe9487ebb8a509a1305574)

![{\ displaystyle t \ in \ lbrack t_ {n} - \ tau _ {i}, t_ {n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f287009ce5d61c9d7ed2a843c93dfdef6226a50)









![{\displaystyle u\in \lbrack 0,h_{n}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/956d5d79b8e61251940a26652b1ecead7daa8b6c)






![{\displaystyle\mathbf{r}^{\intercal}=\left[{\begin{array}{ll}\mathbf{0}_{1\times(d+1)}&1\end{array}}\ вправо],h_{n}\leq \tau}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05fdb2050667c7b12025db96c59b015211204a57)









![{\displaystyle t\in \lbrack t_{0},t_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ed17e1a454d79e9e85aa3fdb316727d17eb069b)

![{\displaystyle т\in \left[t_{0}-\tau, t_{0}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99fafe4165d02d310ce7c3f55c6fbfc1742d2d65)


![{\displaystyle {\frac {d\mathbf {x} \left(t\right)}{dt}} =\mathbf {f} (\mathbf {x} (t),\mathbf {\xi } (t) ),\quad t\in \left[t_{0},T\right],\qquad \qquad \qquad (6.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06e7f4c5cbe530e829f8edf84e2e49d0829a2ef0)





![{\ displaystyle t \ in \ left [t_ {0}, T \ right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aedde214e225a352a24c1c922043d56a7d90588b)





![{\displaystyle \mathbf {M}_{n}=\left[{\begin{array}{ccc}\mathbf {f}_ {\mathbf {x} }\left(\mathbf {y}_{n} ,\mathbf {\xi } (t_{n})\right)&\mathbf {f}_ {\mathbf {\xi } }(\mathbf {y}_{n},\mathbf {\xi } (t_ {n})(\mathbf {\xi } (t_{n+1})-\mathbf {\xi } (t_{n}))/h_{n}&\mathbf {f} \left(\mathbf { y}_{n},\mathbf {\xi } (t_{n})\right)\\0&0&1\\0&0&0\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de2e549c00febeadc80e1df68d44a6a66abd159a)






![{\displaystyle d\mathbf {x} (t)=\mathbf {f} (t,\mathbf {x} (t))dt+\sum \limits _ {i=1}^{m} \mathbf {g} _{i}(t)d\mathbf {w} ^{i}(t),\quad t\in \left[t_{0},T\right],\qquad \qquad \qquad (7.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/464be59af5611f27dd6d946030a7202ce481c427)











![{\displaystyle т\in \lbrack t_ {n},t_ {n+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b15f801777044ac19f6f4e6551c3e78da54f33c5)













![{\displaystyle\mathbf {L} =\left[{\begin{array}{ll}\mathbf{I} &\mathbf{0}_{d\times2}\end{array}}\right],\ mathbf {r}^{\intercal}=\left[{\begin{array}{ll}\mathbf{0}_{1\times(d+1)}&1\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4096111183a23671fc2d181a96e16ca7b7df6d6c)
















![{\displaystyle d\mathbf {x} (t)=\mathbf {f} (t,\mathbf {x} (t))dt+\sum \limits _ {i=1}^{m} \mathbf {g} _{i}(t)d\mathbf {w} ^{i}(t),\qquad t\in \left[t_{0},T\right],\qquad \qquad (8.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4db0bd45e90a7c91e2715a14caf58e220b2e0b36)







![{\ displaystyle \ mathbf {G} (t) = [\ mathbf {g} _ {1} (t), \ ldots, \ mathbf {g} _ {m} (t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12433070ae8deb0a55bf46601f3b7c2b4c410c28)







![{\displaystyle {\mathcal{M}}_{n}=\left[{\begin{array}{cccc}\mathbf{f}_{\mathbf{x}}(t_{n},\mathbf{y }_{n})&\mathbf{GG}^{\intercal}&\mathbf{f}_{t}(t_{n},\mathbf{y}_{n})&\mathbf{f}( t_ {n},\mathbf{y}_{n})\\\mathbf{0}&-\mathbf{f}_{\mathbf{x}}^{\interval }(t_{n},\mathbf {y} _{n})&\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &0&1\\\mathbf {0} &\mathbf {0} &0&0\end {массив}}\right]\in\mathbb{R}^{(2d+2)\times(2d+2)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b6c5cb6cc2c1a036002082a4dcad32b5080660)




![{\displaystyle {\mathcal {M}}_{n}=\left[{\begin{array}{cccccc}\mathbf {J} &\mathbf {H} _{2} &\mathbf {H} _{ 1}&\mathbf {H} _{0}&\mathbf {a} _{2}&\mathbf {a} _{1}\\\mathbf {0} &-\mathbf {J} ^{\intercal }&\mathbf {I} &\mathbf {0} &\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &-\mathbf {J} ^{\intercal } &\mathbf {I} &\mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &\mathbf {0} &-\mathbf {J} ^{\intercal }& \mathbf {0} &\mathbf {0} \\\mathbf {0} &\mathbf {0} &\mathbf {0} &\mathbf {0} &0&1\\\mathbf {0} &\mathbf {0} &\mathbf {0} &\mathbf {0} &0&0\end{array}}\right]\in \mathbb {R} ^{(4d+2)\times (4d+2)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e92d5869bcb0a0b5db4944c8170713c0c5a096a6)



