Ромбитетрагексагональная черепица
| Ромбитетрагексагональная черепица | |
|---|---|
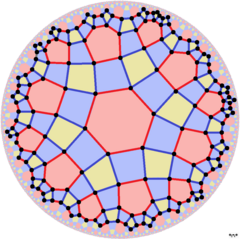
 Модель диска Пуанкаре гиперболической плоскости | |
| Тип | Гиперболическая равномерная мозаика |
| Конфигурация вершин | 4.4.6.4 |
| Символ Шлефли | rr{6,4} или |
| Символ Витхоффа | 4 | 6 2 |
| Диаграмма Кокстера | |
| Группа симметрии | [6,4], (*642) |
| Двойной | Дельтоидная тетрагексагональная мозаика |
| Характеристики | Вершинно-транзитивный |
В геометрии ромбитетрагексагональная мозаика — это равномерная мозаика гиперболической плоскости . Он имеет символ Шлефли rr{6,4}. Его можно рассматривать как построенную в виде выпрямленной тетрагексагональной мозаики r{6,4}, а также расширенной шестиугольной мозаики 4-го порядка или расширенной квадратной мозаики 6-го порядка .
Конструкции
[ редактировать ]Существуют две однородные конструкции этого мозаики: одна из симметрии [6,4] или (*642), а во-вторых, удаление зеркальной середины, [6,1 + ,4], дает прямоугольную фундаментальную область [∞,3,∞], (*3222).
| Имя | Ромбитетрагексагональная черепица | |
|---|---|---|
| Изображение |  |  |
| Симметрия | [6,4] ( *642 ) | [6,1 + ,4] = [∞,3,∞] ( *3222 ) |
| Символ Шлефли | рр{6,4} | т 0,1,2,3 {∞,3,∞} |
| Диаграмма Кокстера |
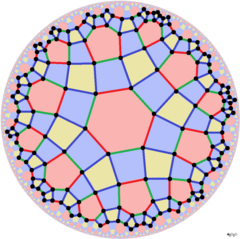
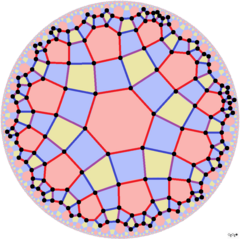
Если включить раскраску краев, можно увидеть три формы более низкой симметрии: ![]()
![]()
![]()
![]()
![]() видит шестиугольники как усеченные треугольники с двумя цветными краями, с [6,4 + ] (4*3) симметрия.
видит шестиугольники как усеченные треугольники с двумя цветными краями, с [6,4 + ] (4*3) симметрия. ![]()
![]()
![]()
![]()
![]() видит желтые квадраты как прямоугольники с двумя цветными краями, с [6 + ,4] (6*2) симметрия. Симметрия последней четверти объединяет эти раскраски с [6 + ,4 + ] (32×) симметрия, с 2- и 3-кратными точками вращения и скользящими отражениями.
видит желтые квадраты как прямоугольники с двумя цветными краями, с [6 + ,4] (6*2) симметрия. Симметрия последней четверти объединяет эти раскраски с [6 + ,4 + ] (32×) симметрия, с 2- и 3-кратными точками вращения и скользящими отражениями.
| Конструкции более низкой симметрии |
|---|
Эта четырехцветная мозаика связана с полуправильным бесконечным косым многогранником с той же фигурой вершин в евклидовом трехмерном пространстве с призматической сотовой конструкцией ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Симметрия
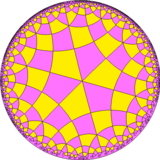
[ редактировать ]Двойная мозаика, называемая дельтоидной тетрагексагональной мозаикой , представляет собой фундаментальные области орбифолда *3222, показанного здесь из трех разных центров. Его основной областью является четырехугольник Ламберта с тремя прямыми углами. Эту симметрию можно увидеть из треугольной симметрии [6,4], (*642) с удаленным одним зеркалом, построенной как [6,1 + ,4], (*3222). Удаление половины синих зеркал снова удваивает домен до симметрии *3322.
Связанные многогранники и мозаика
[ редактировать ]| * n 42 мутация симметрии расширенных мозаик: n .4.4.4 |
|---|
| Однородные тетрагексагональные мозаики |
|---|
| Однородные мозаики по симметрии *3222 |
|---|
См. также
[ редактировать ]- Квадратная плитка
- Замощения правильных многоугольников
- Список однородных плоских мозаик
- Список правильных многогранников
Ссылки
[ редактировать ]- Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
- «Глава 10: Правильные соты в гиперболическом пространстве». Красота геометрии: двенадцать эссе . Дуврские публикации. 1999. ISBN 0-486-40919-8 . LCCN 99035678 .
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Гиперболическая мозаика» . Математический мир .
- Вайсштейн, Эрик В. «Гиперболический диск Пуанкаре» . Математический мир .
- Галерея гиперболических и сферических плиток
- KaleidoTile 3: образовательное программное обеспечение для создания сферических, плоских и гиперболических мозаик.
- Гиперболические плоские мозаики, Дон Хэтч