Подъемное имущество

В математике , в частности в теории категорий , свойство подъема — это свойство пары морфизмов в категории . Он используется в теории гомотопий в рамках алгебраической топологии для определения свойств морфизмов, начиная с явно заданного класса морфизмов. Это заметно проявляется в теории модельных категорий , аксиоматической структуре теории гомотопий, введенной Дэниелом Квилленом . Он также используется в определении системы факторизации и слабой системы факторизации — понятий, связанных с понятием модельной категории, но менее ограничительных. Некоторые элементарные понятия также могут быть выражены с использованием свойства подъема, начиная со списка (контр)примеров.

Формальное определение

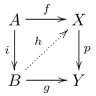
Морфизм $i$ в категории обладает свойством левого подъема относительно морфизма $p$, и $p$ также имеет право подъемного свойства в отношении $i$, иногда обозначаемый $i\perp p$ или $i\downarrow p$, тогда и только тогда, когда для каждого морфизма имеет место следующая импликация $f$ и $g$ в категории:

• если внешний квадрат следующей диаграммы коммутирует, то существует $h$ завершения диаграммы, т.е. для каждого $f:A\to X$ и $g:B\to Y$ такой, что $p\circ f=g\circ i$ существует $h:B\to X$ такой, что $h\circ i=f$ и $p\circ h=g$.

Иногда это также называют морфизмом $i$ ортогональна морфизму ​ $p$; однако это также может относиться кболее сильное свойство, которое всякий раз, когда $f$ и $g$ такие же, как и выше, диагональный морфизм $h$ существует и также должен быть уникальным.

Для класса $C$ морфизмов в категории, ее левый ортогонал $C^{\perp \ell }$ или $C^{\perp }$ по подъемному свойству, соответственно, его право ортогональному $C^{\perp r}$ или ${}^{\perp }C$, является классом всех морфизмов, которые обладают левым и соответственно правым свойством подъема относительно каждого морфизма в классе $C$. В обозначениях

$${\begin{aligned}C^{\perp \ell }&:=\{i\mid \forall p\in C,i\perp p\}\\C^{\perp r}&:=\{p\mid \forall i\in C,i\perp p\}\end{aligned}}$$

Взяв ортогональ класса $C$ - это простой способ определить класс морфизмов, исключая неизоморфизмы из $C$, что полезно при вычислении погони за диаграммой .

в категории Множество множеств Таким образом , правый ортогональный $\{\emptyset \to \{*\}\}^{\perp r}$ простейшей несюръекции $\emptyset \to \{*\},$ — класс сюръекций. Левый и правый ортогонали $\{x_{1},x_{2}\}\to \{*\},$ простейшие неинъекции , оба являются именно классом инъекций,

$$\{\{x_{1},x_{2}\}\to \{*\}\}^{\perp \ell }=\{\{x_{1},x_{2}\}\to \{*\}\}^{\perp r}=\{f\mid f{\text{ is an injection }}\}.$$

Ясно, что $C^{\perp \ell r}\supset C$ и $C^{\perp r\ell }\supset C$. Класс $C^{\perp r}$ всегда замкнут относительно ретрактов, откатов , (маленьких) произведений (если они существуют в категории) и композиции морфизмов и содержит все изоморфизмы (то есть обратимые морфизмы) базовой категории. Тем временем, $C^{\perp \ell }$ замкнут относительно ретрактов, выталкиваний , (маленьких) копродукций и трансфинитной композиции ( фильтрованных копределов ) морфизмов (всякий раз, когда они существуют в категории), а также содержит все изоморфизмы.

Примеры

Ряд понятий можно определить, перейдя несколько раз к левой или правой ортогонали, начиная со списка явных примеров, т. е. как $C^{\perp \ell },C^{\perp r},C^{\perp \ell r},C^{\perp \ell \ell }$, где $C$ — класс, состоящий из нескольких явно заданных морфизмов. Полезно предположить, что свойство левого подъема класса $C$ это своего рода отрицаниесвойства находиться в $C$, и что подъем вправо – это тоже своего рода отрицание. Следовательно, классы, полученные из $C$ взяв ортогонали нечетное количество раз, например $C^{\perp \ell },C^{\perp r},C^{\perp \ell r\ell },C^{\perp \ell \ell \ell }$ и т. д., представляют собой различные виды отрицания $C$, так $C^{\perp \ell },C^{\perp r},C^{\perp \ell r\ell },C^{\perp \ell \ell \ell }$ каждый состоит из морфизмов, далеких от свойства $C$.

Примеры подъемных свойств в алгебраической топологии

Карта $f:U\to B$ имеет свойство подъема пути, если и только если $\{0\}\to [0,1]\perp f$ где $\{0\}\to [0,1]$ – это включение одной конечной точки отрезка в интервал $[0,1]$.

Карта $f:U\to B$ обладает свойством поднятия гомотопий тогда и только тогда, когда $X\to X\times [0,1]\perp f$ где $X\to X\times [0,1]$ это карта $x\mapsto (x,0)$.

Примеры несущих свойств из категорий моделей

Расслоения и кофибрации.

• Пусть Top — категория топологических пространств и пусть $C_{0}$ быть классом карт $S^{n}\to D^{n+1}$, вложения границы $S^{n}=\partial D^{n+1}$ мяча в мяч $D^{n+1}$. Позволять $WC_{0}$ — класс отображений, вложивших верхнюю полусферу в диск. $WC_{0}^{\perp \ell },WC_{0}^{\perp \ell r},C_{0}^{\perp \ell },C_{0}^{\perp \ell r}$ — это классы расслоений, ациклических корасслоений, ациклических расслоений и корасслоений.

• Пусть sSet — категория симплициальных множеств . Позволять $C_{0}$ — класс граничных включений $\partial \Delta [n]\to \Delta [n]$, и пусть $WC_{0}$ быть классом роговых включений $\Lambda ^{i}[n]\to \Delta [n]$. Тогда классы расслоений, ациклических корасслоений, ациклических расслоений и корасслоений равны соответственно $WC_{0}^{\perp \ell },WC_{0}^{\perp \ell r},C_{0}^{\perp \ell },C_{0}^{\perp \ell r}$.

• Позволять $\mathbf {Ch} (R)$ — категория цепных комплексов над коммутативным кольцом $R$. Позволять $C_{0}$ быть классом отображений формы

$$\cdots \to 0\to R\to 0\to 0\to \cdots \to \cdots \to R{\xrightarrow {\operatorname {id} }}R\to 0\to 0\to \cdots ,$$

и $WC_{0}$ быть

$$\cdots \to 0\to 0\to 0\to 0\to \cdots \to \cdots \to R{\xrightarrow {\operatorname {id} }}R\to 0\to 0\to \cdots .$$

Затем $WC_{0}^{\perp \ell },WC_{0}^{\perp \ell r},C_{0}^{\perp \ell },C_{0}^{\perp \ell r}$ — это классы расслоений, ациклических корасслоений, ациклических расслоений и корасслоений.

Элементарные примеры в различных категориях

В наборе ,

• $\{\emptyset \to \{*\}\}^{\perp r}$ это класс сюръекций,

• $(\{a,b\}\to \{*\})^{\perp r}=(\{a,b\}\to \{*\})^{\perp \ell }$ это класс инъекций.

В категории $R{\text{-}}\mathbf {Mod}$ модулей над коммутативным кольцом $R$,

• $\{0\to R\}^{\perp r},\{R\to 0\}^{\perp r}$ — класс сюръекций, соотв. инъекции,

• Модуль $M$ является проективным , соотв. инъективный , если и только если $0\to M$ находится в $\{0\to R\}^{\perp r\ell }$, соотв. $M\to 0$ находится в $\{R\to 0\}^{\perp rr}$.

В категории $\mathbf {Grp}$ групп ​ ,

• $\{\mathbb {Z} \to 0\}^{\perp r}$, соотв. $\{0\to \mathbb {Z} \}^{\perp r}$, — класс инъекций, соотв. сюръективы (где $\mathbb {Z}$ обозначает бесконечную циклическую группу ),

• Группа $F$ это свободная группа, если и только если $0\to F$ находится в $\{0\to \mathbb {Z} \}^{\perp r\ell },$

• Группа $A$ только без кручения, если $0\to A$ находится в $\{n\mathbb {Z} \to \mathbb {Z} :n>0\}^{\perp r},$

• Подгруппа ​ $A$ из $B$ это чисто тогда и только тогда $A\to B$ находится в $\{n\mathbb {Z} \to \mathbb {Z} :n>0\}^{\perp r}.$

Для конечной группы $G$,

• $\{0\to {\mathbb {Z} }/p{\mathbb {Z} }\}\perp 1\to G$ если порядок ​ $G$ является основным для $p$ если только $\{{\mathbb {Z} }/p{\mathbb {Z} }\to 0\}\perp G\to 1$,

• $G\to 1\in (0\to {\mathbb {Z} }/p{\mathbb {Z} })^{\perp rr}$ если только $G$ это $p$-группа ,

• $H$ нильпотентен тогда и только тогда, когда диагональное отображение $H\to H\times H$ находится в $(1\to *)^{\perp \ell r}$ где $(1\to *)$ обозначает класс отображений $\{1\to G:G{\text{ arbitrary}}\},$

• конечная группа $H$ разрешимо только тогда, когда тогда и $1\to H$ находится в
  $$\{0\to A:A{\text{ abelian}}\}^{\perp \ell r}=\{[G,G]\to G:G{\text{ arbitrary }}\}^{\perp \ell r}.$$

В категории $\mathbf {Top}$ топологических пространств, пусть $\{0,1\}$, соотв. $\{0\leftrightarrow 1\}$ обозначают дискретный , соотв. антидискретное пространство с двумя точками 0 и 1. Пусть $\{0\to 1\}$ обозначим пространство Серпинского двух точек, где точка 0 открыта, а точка 1 закрыта, и пусть $\{0\}\to \{0\to 1\},\{1\}\to \{0\to 1\}$ и т. д. обозначают очевидные вложения.

• пространство $X$ удовлетворяет аксиоме разделения T ₀ тогда и только тогда, когда $X\to \{*\}$ находится в $(\{0\leftrightarrow 1\}\to \{*\})^{\perp r},$

• пространство $X$ удовлетворяет аксиоме разделения T ₁ тогда и только тогда, когда $\emptyset \to X$ находится в $(\{0\to 1\}\to \{*\})^{\perp r},$

• $(\{1\}\to \{0\to 1\})^{\perp \ell }$ — класс карт с плотным изображением ,

• $(\{0\to 1\}\to \{*\})^{\perp \ell }$ это класс карт $f:X\to Y$ такая, что топология на $A$ это откат топологии на $B$, то есть топология на $A$ — топология с наименьшим количеством открытых множеств, такая, что отображение непрерывно ,

• $(\emptyset \to \{*\})^{\perp r}$ — класс сюръективных отображений,

• $(\emptyset \to \{*\})^{\perp r\ell }$ — класс карт формы $A\to A\cup D$ где $D$ является дискретным,

• $(\emptyset \to \{*\})^{\perp r\ell \ell }=(\{a\}\to \{a,b\})^{\perp \ell }$ это класс карт $A\to B$ такая, что каждая компонента связности $B$ пересекает $\operatorname {Im} A$,

• $(\{0,1\}\to \{*\})^{\perp r}$ — класс инъективных отображений,

• $(\{0,1\}\to \{*\})^{\perp \ell }$ это класс карт $f:X\to Y$ такой, что прообраз связного замкнутого открытого подмножества $Y$ является связным замкнутым подмножеством открытым $X$, например $X$ подключен тогда и только тогда, когда $X\to \{*\}$ находится в $(\{0,1\}\to \{*\})^{\perp \ell }$,

• для подключенного пространства $X$, каждая непрерывная функция на $X$ ограничен тогда и только тогда, когда $\emptyset \to X\perp \cup _{n}(-n,n)\to \mathbb {R}$ где $\cup _{n}(-n,n)\to \mathbb {R}$ это карта несвязного объединения открытых интервалов $(-n,n)$ в реальную линию $\mathbb {R} ,$

• пространство $X$ является Хаусдорфом тогда и только тогда, когда для любого инъективного отображения $\{a,b\}\hookrightarrow X$, оно держится $\{a,b\}\hookrightarrow X\perp \{a\to x\leftarrow b\}\to \{*\}$ где $\{a\leftarrow x\to b\}$ обозначает трехточечное пространство с двумя открытыми точками $a$ и $b$, и закрытая точка $x$,

• пространство $X$ это совершенно нормально , если только $\emptyset \to X\perp [0,1]\to \{0\leftarrow x\to 1\}$ где открытый интервал $(0,1)$ идет в $x$, и $0$ карты в точку $0$, и $1$ карты в точку $1$, и $\{0\leftarrow x\to 1\}$ обозначает трехточечное пространство с двумя замкнутыми точками $0,1$ и одна открытая точка $x$.

В категории метрических пространств с равномерно непрерывными отображениями.

• Пространство $X$ является полным, если и только если $\{1/n\}_{n\in \mathbb {N} }\to \{0\}\cup \{1/n\}_{n\in \mathbb {N} }\perp X\to \{0\}$ где $\{1/n\}_{n\in \mathbb {N} }\to \{0\}\cup \{1/n\}_{n\in \mathbb {N} }$ - очевидное включение между двумя подпространствами вещественной прямой с индуцированной метрикой, и $\{0\}$ — метрическое пространство, состоящее из одной точки,

• Подпространство $i:A\to X$ закрыто, если только $\{1/n\}_{n\in \mathbb {N} }\to \{0\}\cup \{1/n\}_{n\in \mathbb {N} }\perp A\to X.$

Ссылки

• Хови, Марк (1999). Категории моделей .