Осевой ток

Осевой ток , также называемый псевдовекторным или киральным током, представляет собой сохраняющийся ток, связанный с киральной симметрией или осевой симметрией системы.

Источник

Согласно теореме Нётер , каждой симметрии системы соответствует сохраняющаяся величина. Например, вращательная инвариантность системы подразумевает сохранение ее углового момента , или пространственно-временная инвариантность предполагает сохранение энергии-импульса. В теории поля квантовой внутренняя симметрия также приводит к сохранению величин. Например, U(1) преобразование КЭД калибровочное предполагает сохранение электрического заряда . Аналогично, если теория обладает внутренней киральной или осевой симметрией, будет сохраняться величина, называемая осевым зарядом . Кроме того, подобно тому, как движение электрически заряженной частицы создает электрический ток , движущийся осевой заряд представляет собой осевой ток.

Определение

Осевой ток, возникающий в результате движения аксиально заряженной движущейся частицы, формально определяется как $j_{5}^{\mu }={\overline {\psi }}\gamma ^{5}\gamma ^{\mu }\psi$, где $\psi$ - поле частицы , представленное спинором Дирака (поскольку частица обычно представляет собой со спином -1/2 фермион ) и $\gamma ^{5}$ и $\gamma ^{\mu }$ — Дирака гамма-матрицы .

Для сравнения: электромагнитный ток, создаваемый электрически заряженной движущейся частицей, равен $j^{\mu }={\overline {\psi }}\gamma ^{\mu }\psi$.

Значение

Как объяснялось выше, аксиальный ток является просто эквивалентом электромагнитного тока для осевой симметрии, а не для симметрии U (1). Другая точка зрения открывается, если вспомнить, что киральная симметрия - это инвариантность теории относительно вращения поля $\psi _{\rm {L}}\rightarrow e^{i\theta _{\rm {L}}}\psi _{\rm {L}}$ и $\psi _{\rm {R}}\rightarrow \psi _{\rm {R}}$ (или альтернативно $\psi _{\rm {L}}\rightarrow \psi _{\rm {L}}$ и $\psi _{\rm {R}}\rightarrow e^{i\theta _{\rm {R}}}\psi _{\rm {R}}$), где $\psi _{\rm {L}}$ обозначает левое поле и $\psi _{\rm {R}}$ правша. Из этого, а также из того, что $\psi =\psi _{\rm {L}}+\psi _{\rm {R}}$ и определение $j_{5}^{\mu }$ Выше видно, что аксиальный ток представляет собой разницу между током левых фермионов и током правых, тогда как электромагнитный ток представляет собой сумму.

Киральную симметрию демонстрируют векторные калибровочные теории с безмассовыми фермионами. Поскольку в природе не существует известных безмассовых фермионов, киральная симметрия является в лучшем случае приблизительной симметрией в фундаментальных теориях, и аксиальный ток не сохраняется. (Примечание: это явное нарушение киральной симметрии ненулевыми массами не следует путать со спонтанным нарушением киральной симметрии , которое играет доминирующую роль в адронной физике .) Важным следствием такого несохранения является нейтрального пиона распад и киральная аномалия , что напрямую связано с шириной распада пиона .

Приложения

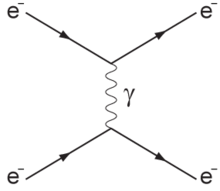
Осевой ток является важной частью формализма, описывающего реакции рассеяния при высоких энергиях . В такой реакции две частицы разлетаются друг от друга, обменивая силовой бозон , например фотон , на электромагнитное рассеяние (см. рисунок).

Диаграмма Фейнмана рассеяния двух электронов при испускании виртуального фотона .

Сечение , которая, в свою очередь , такой реакции пропорционально квадрату амплитуды рассеяния определяется произведением бозонного пропагатора на два тока, связанных с движением двух сталкивающихся частиц. Таким образом, токи (аксиальные или электромагнитные) являются одним из двух основных ингредиентов, необходимых для расчета высокоэнергетического рассеяния , а другой — распространителем бозона .

электронов на нуклонах При рассеянии (или, в более общем плане, при рассеянии заряженных лептонов на адроны и ядрах ) аксиальный ток дает спин -зависимую часть сечения . (Средняя по спину часть сечения возникает из-за электромагнитного тока. )

При нейтрино -нуклонном рассеянии нейтрино взаимодействуют только посредством аксиального тока, таким образом получая иную информацию о структуре нуклона, чем в случае заряженных лептонов.

Нейтральные пионы также взаимодействуют только через аксиальный ток, поскольку пионы являются псевдоскалярными частицами, и для создания амплитуд (скалярных величин) пион должен соединяться с другим псевдоскалярным объектом, например с аксиальным током. (Заряженные пионы также могут связываться посредством электромагнитного тока.)

См. также

• Киральная аномалия
• КХД
• Нарушение киральной симметрии
• Киральная теория возмущений
• Хиральный магнитный эффект
• Паритет (физика)