Ориентация (геометрия)

В геометрии ориентация положение , направление , пространстве , направление или угловое положение объекта (например, линии , плоскости или твердого тела ) является частью описания того, как он размещается в , которое он занимает. ^{[ 1 ]} Более конкретно, это относится к воображаемому повороту , необходимому для перемещения объекта из исходного положения в его текущее положение. Вращения может быть недостаточно для достижения текущего положения, и в этом случае может потребоваться добавить воображаемый сдвиг объекта для изменения положения (или линейного положения). Положение и ориентация вместе полностью описывают, как объект размещается в пространстве. Можно думать, что вышеупомянутое воображаемое вращение и перемещение происходят в любом порядке, поскольку ориентация объекта не меняется при его перемещении, а его положение не меняется при вращении.

Теорема Эйлера о вращении показывает, что в трех измерениях любой ориентации можно достичь одним поворотом вокруг фиксированной оси . Это дает один общий способ представления ориентации с использованием представления оси-угла . Другие широко используемые методы включают кватернионы вращения , роторы , углы Эйлера или матрицы вращения . Более специализированное использование включает индексы Миллера в кристаллографии, простирание и падение в геологии, а также оценки на картах и знаках. Единичный вектор объекта также может использоваться для представления ориентации вектора нормали или относительного направления между двумя точками.

Обычно ориентация задается относительно системы отсчета , обычно определяемой декартовой системой координат . Говорят, что два объекта, имеющие одно и то же направление, сонаправлены (как в случае с параллельными линиями ). Два направления называются противоположными, если они являются аддитивными инверсиями друг друга, как в случае с произвольным единичным вектором и его умножением на -1. Два направления являются тупыми, если они образуют тупой угол (больше прямого угла) или, что то же самое, если их скалярное произведение или скалярная проекция отрицательны.

Математические представления

Три измерения

В общем случае положение и ориентация в пространстве твердого тела определяются как положение и ориентация относительно основной системы отсчета другой системы отсчета, которая фиксирована относительно тела и, следовательно, перемещается и вращается вместе с ним (тело местная система отсчета или местная система координат ). Для описания ориентации этой локальной системы координат необходимы как минимум три независимых значения. Три других значения описывают положение точки на объекте. Все точки тела при вращении меняют свое положение, кроме тех, которые лежат на оси вращения. Если твердое тело обладает вращательной симметрией, не все ориентации различимы, кроме как путем наблюдения за тем, как ориентация меняется во времени от известной исходной ориентации. Например, ориентацию в пространстве линии , сегмента линии или вектора можно указать только двумя значениями, например двумя направляющими косинусами . Другим примером является положение точки на Земле, часто описываемое с использованием ориентации линии, соединяющей ее с центром Земли, измеренной с использованием двух углов долгота и широта . Аналогично, ориентацию плоскости можно описать двумя значениями, например, задав ориентацию линии, нормальной к этой плоскости, или используя углы простирания и падения.

Более подробная информация о математических методах представления ориентации твердых тел и плоскостей в трех измерениях приведена в следующих разделах.

Два измерения

В двух измерениях ориентация любого объекта (линии, вектора или плоской фигуры ) задается одним значением: углом, на который он повернулся. Существует только одна степень свободы и только одна неподвижная точка, вокруг которой происходит вращение.

Несколько измерений

Когда имеется $d$ измерений, для указания ориентации объекта, не имеющего вращательной симметрии, требуется $d (d - 1)/2$ независимых значений.

Твердое тело в трех измерениях

Было разработано несколько методов описания ориентации твердого тела в трех измерениях. Они обобщены в следующих разделах.

углы Эйлера

Первая попытка представления ориентации приписывается Леонарду Эйлеру . Он представил себе три системы отсчета, которые могли вращаться одна вокруг другой, и понял, что, начав с фиксированной системы отсчета и выполнив три вращения, он может получить любую другую систему отсчета в пространстве (используя два вращения для фиксации вертикальной оси и еще одно для фиксации вертикальной оси). зафиксируйте две другие оси). Значения этих трех поворотов называются углами Эйлера .

Углы Тейта – Брайана

Это три угла, также известные как рыскание, тангаж и крен, углы навигации и углы кардана. Математически они представляют собой набор из шести возможностей внутри двенадцати возможных наборов углов Эйлера, причем этот порядок лучше всего использовать для описания ориентации транспортного средства, например самолета. В аэрокосмической технике их обычно называют углами Эйлера.

Вектор ориентации

Эйлер также понял, что композиция двух вращений эквивалентна одному вращению вокруг другой фиксированной оси ( теорема Эйлера о вращении ). Следовательно, композиция первых трех углов должна быть равна всего лишь одному повороту, ось которого было сложно вычислить, пока не были разработаны матрицы.

На основании этого он ввел векторный способ описания любого вращения с вектором на оси вращения и модулем, равным значению угла. Следовательно, любую ориентацию можно представить вектором вращения (также называемым вектором Эйлера), ведущим к ней из системы отсчета. Когда вектор вращения используется для представления ориентации, его обычно называют вектором ориентации или вектором отношения.

Похожий метод, называемый представлением оси-угла , описывает вращение или ориентацию с использованием единичного вектора, совмещенного с осью вращения, и отдельного значения для обозначения угла (см. рисунок).

Матрица ориентации

С введением матриц теоремы Эйлера были переписаны. Вращения описывались ортогональными матрицами, называемыми матрицами вращения или матрицами направленного косинуса. При использовании для представления ориентации матрицу вращения обычно называют матрицей ориентации или матрицей отношения.

Вышеупомянутый вектор Эйлера является собственным вектором матрицы вращения (матрица вращения имеет уникальное действительное собственное значение ). Произведение двух матриц вращения представляет собой композицию вращений. Поэтому, как и раньше, ориентацию можно задать как поворот от исходного кадра до достижения кадра, который мы хотим описать.

Конфигурационное пространство несимметричного n объекта в n -мерном пространстве — это SO ) ( × R ^н. основу из касательных векторов Ориентацию можно визуализировать, прикрепив к объекту . Направление, в котором указывает каждый вектор, определяет его ориентацию.

Кватернион ориентации

Другой способ описания вращения — использование кватернионов вращения , также называемых версорами. Они эквивалентны матрицам вращения и векторам вращения. Что касается векторов вращения, их легче преобразовывать в матрицы и обратно. При использовании для представления ориентации кватернионы вращения обычно называются кватернионами ориентации или кватернионами ориентации.

Плоскость в трех измерениях

Индексы Миллера

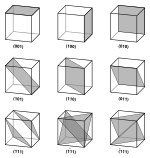
Отношение плоскости решетки - это ориентация линии, нормальной к плоскости, ^{[ 2 ]} самолета и описывается индексами Миллера . В трехмерном пространстве семейство плоскостей (серия параллельных плоскостей) можно обозначить индексами Миллера ( hkl ), ^{[ 3 ]}^{[ 4 ]} поэтому семейство планов имеет отношение, общее для всех составляющих его планов.

Удар и падение

Линия простирания и падение плоскости, описывающее положение относительно горизонтальной плоскости и вертикальной плоскости, перпендикулярной линии простирания.

Многие объекты, наблюдаемые в геологии, представляют собой плоскости или линии, и их ориентацию обычно называют их положением . Эти отношения задаются двумя углами.

Для линии эти углы называются трендом и впадиной . Тренд — это направление линии по компасу, а погружение — это угол вниз, который она образует с горизонтальной плоскостью. ^{[ 5 ]}

Для плоскости два угла называются простиранием (угол) и падением (угол) . Линия простирания — это пересечение горизонтальной плоскости с наблюдаемым плоским объектом (и, следовательно, горизонтальной линией), а угол простирания — это направление этой линии (то есть относительно географического севера или от магнитного севера ). Падение представляет собой угол между горизонтальной плоскостью и наблюдаемым плоским элементом, наблюдаемым в третьей вертикальной плоскости, перпендикулярной линии простирания.

Примеры использования

Твердое тело

Ориентация твердого тела определяется тремя углами

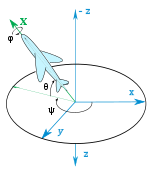
Положение твердого тела — это его ориентация, описываемая, например, ориентацией системы координат, закрепленной в теле, относительно фиксированной системы отсчета. Отношение описывается координатами положения и состоит как минимум из трех координат. ^{[ 6 ]} Одна из схем ориентации твердого тела основана на вращении осей тела; тела последовательные вращения три раза вокруг осей фиксированной системы отсчета тела, тем самым устанавливая углы Эйлера . ^{[ 7 ]}^{[ 8 ]} Другой основан на крене, тангаже и рыскании . ^{[ 9 ]} хотя эти термины также относятся к дополнительным отклонениям от номинального положения.

См. также

Ссылки

^ Роберт Дж. Твисс; Элдридж М. Мурс (1992). «§2.1 Ориентация конструкций» . Структурная геология (2-е изд.). Макмиллан. п. 11. ISBN 0-7167-2252-6 . ... положение плоскости или линии, то есть ее ориентация в пространстве, имеет фундаментальное значение для описания структур.
^ Уильям Энтони Грэнвилл (1904). «§178 Нормальная линия к поверхности». Элементы дифференциального и интегрального исчисления . Джинн и компания. п. 275 .
^ Огастес Эдвард Хаф Лав (1892). Трактат по математической теории упругости . Том. 1. Издательство Кембриджского университета. п. 79 и далее .
^ Маркус Фредерик Чарльз Лэдд; Рекс Альфред Палмер (2003). «§2.3 Семейства плоскостей и межплоскостные расстояния» . Определение структуры методом рентгеновской кристаллографии (4-е изд.). Спрингер. п. 62 и далее . ISBN 0-306-47454-9 .
^ Стивен Марк Роуленд; Эрнест М. Дюбендорфер; Ильза М. Шифельбейн (2007). «Отношения линий и плоскостей» . Структурный анализ и синтез: Лабораторный курс структурной геологии (3-е изд.). Уайли-Блэквелл. п. 1 и далее . ISBN 978-1-4051-1652-7 .
^ Ханспетер Шауб ; Джон Л. Джанкинс (2003). «Кинематика твердого тела» . Аналитическая механика космических систем . Американский институт аэронавтики и астронавтики. п. 71. ИСБН 1-56347-563-4 .
^ Джек Б. Койперс (2002). «Рисунок 4.7: Последовательность углов Эйлера для самолета» . Кватернионы и последовательности вращения: введение в приложения к орбитам, аэрокосмической отрасли и виртуальной реальности . Издательство Принстонского университета. п. 85. ИСБН 0-691-10298-8 .
^ Бонг Ви (1998). «§5.2 Углы Эйлера». Динамика и управление космическим аппаратом . Американский институт аэронавтики и астронавтики. п. 310 . ISBN 1-56347-261-9 . Положение твердого тела под углом Эйлера.
^ Лоренцо Скьявикко; Бруно Сицилиано (2000). «§2.4.2 Углы крена – тангажа – рыскания» . Моделирование и управление роботами-манипуляторами (2-е изд.). Спрингер. п. 32. ISBN 1-85233-221-2 .

Внешние ссылки

СМИ, связанные с ориентацией (математикой), на Викискладе?

[Moores-1] Роберт Дж. Твисс; Элдридж М. Мурс (1992). «§2.1 Ориентация конструкций» . Структурная геология (2-е изд.). Макмиллан. п. 11. ISBN 0-7167-2252-6 . ... положение плоскости или линии, то есть ее ориентация в пространстве, имеет фундаментальное значение для описания структур.

[Granville-2] Уильям Энтони Грэнвилл (1904). «§178 Нормальная линия к поверхности». Элементы дифференциального и интегрального исчисления . Джинн и компания. п. 275 .

[Love-3] Огастес Эдвард Хаф Лав (1892). Трактат по математической теории упругости . Том. 1. Издательство Кембриджского университета. п. 79 и далее .

[Ladd-4] Маркус Фредерик Чарльз Лэдд; Рекс Альфред Палмер (2003). «§2.3 Семейства плоскостей и межплоскостные расстояния» . Определение структуры методом рентгеновской кристаллографии (4-е изд.). Спрингер. п. 62 и далее . ISBN 0-306-47454-9 .

[Rowland-5] Стивен Марк Роуленд; Эрнест М. Дюбендорфер; Ильза М. Шифельбейн (2007). «Отношения линий и плоскостей» . Структурный анализ и синтез: Лабораторный курс структурной геологии (3-е изд.). Уайли-Блэквелл. п. 1 и далее . ISBN 978-1-4051-1652-7 .

[Schaub-6] Ханспетер Шауб ; Джон Л. Джанкинс (2003). «Кинематика твердого тела» . Аналитическая механика космических систем . Американский институт аэронавтики и астронавтики. п. 71. ИСБН 1-56347-563-4 .

[Kuipers-7] Джек Б. Койперс (2002). «Рисунок 4.7: Последовательность углов Эйлера для самолета» . Кватернионы и последовательности вращения: введение в приложения к орбитам, аэрокосмической отрасли и виртуальной реальности . Издательство Принстонского университета. п. 85. ИСБН 0-691-10298-8 .

[Wie-8] Бонг Ви (1998). «§5.2 Углы Эйлера». Динамика и управление космическим аппаратом . Американский институт аэронавтики и астронавтики. п. 310 . ISBN 1-56347-261-9 . Положение твердого тела под углом Эйлера.

[Sciavicco-9] Лоренцо Скьявикко; Бруно Сицилиано (2000). «§2.4.2 Углы крена – тангажа – рыскания» . Моделирование и управление роботами-манипуляторами (2-е изд.). Спрингер. п. 32. ISBN 1-85233-221-2 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]