Активная и пассивная трансформация

При активном преобразовании (слева) точка $P$ преобразуется в точку $P'$ путем поворота по часовой стрелке на угол $θ$ вокруг начала координат фиксированной системы координат. При пассивном преобразовании (справа) точка $P$ остается неподвижной, а система координат поворачивается против часовой стрелки на угол $θ$ относительно своего начала координат. Координаты $P'$ после активного преобразования относительно исходной системы координат такие же, как координаты $P$ относительно повернутой системы координат.

Геометрические преобразования можно разделить на два типа: активные преобразования или преобразования алиби , которые изменяют физическое положение набора точек относительно фиксированной системы отсчета или системы координат ( алиби означает «нахождение где-то в другом месте в одно и то же время»); и пассивные преобразования или преобразования псевдонимов , которые оставляют точки фиксированными, но меняют систему отсчета или систему координат, относительно которой они описаны ( псевдоним означает «переходить под другим именем»). ^[1]^[2] Под трансформацией могут иметь в виду и то , математики обычно подразумевают активные трансформации, тогда как физики и инженеры и другое. ^{[ нужна ссылка ]}

Например, активные преобразования полезны для описания последовательных положений твердого тела . С другой стороны, пассивные преобразования могут быть полезны при анализе движений человека, чтобы наблюдать движение большеберцовой кости относительно бедренной кости , то есть ее движение относительно ( локальной ) системы координат, которая движется вместе с бедренной костью, а не (локальной) системой координат, которая движется вместе с бедренной костью. глобальная ) система координат, привязанная к полу. ^[2]

В трехмерном евклидовом пространстве любое правильное жесткое преобразование , активное или пассивное, может быть представлено как винтовое смещение , сочетание перемещения вдоль оси и вращения вокруг этой оси.

Термины «активное преобразование» и «пассивное преобразование» были впервые введены в 1957 году Валентином Баргманном для описания преобразований Лоренца в специальной теории относительности . ^[3]

Пример [ править ]

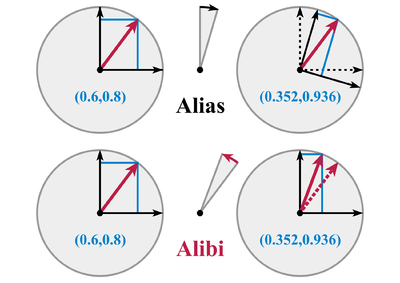
В качестве примера пусть вектор $\mathbf {v} =(v_{1},v_{2})\in \mathbb {R} ^{2}$ , быть вектором на плоскости. Поворот вектора на угол θ против часовой стрелки задается матрицей вращения : $R={\begin{pmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{pmatrix}},$ которое можно рассматривать либо как активное преобразование , либо как пассивное преобразование (где приведенная выше матрица будет инвертирована ), как описано ниже.

Пространственные преобразования в евклидовом пространстве R ³[ редактировать ]

В общем пространственная трансформация $T\colon \mathbb {R} ^{3}\to \mathbb {R} ^{3}$ может состоять из перевода и линейного преобразования. В дальнейшем перевод будет опущен, а линейное преобразование будет представлено матрицей 3×3. $T$ .

трансформация Активная

В качестве активной трансформации $T$ преобразует исходный вектор $\mathbf {v} =(v_{x},v_{y},v_{z})$ в новый вектор $\mathbf {v} '=(v'_{x},v'_{y},v'_{z})=T\mathbf {v} =T(v_{x},v_{y},v_{z})$ .

Если человек просматривает $\{\mathbf {e} '_{x}=T(1,0,0),\ \mathbf {e} '_{y}=T(0,1,0),\ \mathbf {e} '_{z}=T(0,0,1)\}$ в качестве нового базиса , то координаты нового вектора $\mathbf {v} '=v_{x}\mathbf {e} '_{x}+v_{y}\mathbf {e} '_{y}+v_{z}\mathbf {e} '_{z}$ в новой базе такие же, как и в $\mathbf {v} =v_{x}\mathbf {e} _{x}+v_{y}\mathbf {e} _{y}+v_{z}\mathbf {e} _{z}$ в исходной основе. Обратите внимание, что активные преобразования имеют смысл даже в качестве линейного преобразования в другое векторное пространство . Имеет смысл записывать новый вектор в базисе без штриха (как указано выше) только тогда, когда преобразование происходит из пространства в себя.

Пассивная трансформация [ править ]

С другой стороны, когда кто-то смотрит $T$ в качестве пассивного преобразования исходный вектор $\mathbf {v} =(v_{x},v_{y},v_{z})$ остается неизменным, а система координат и ее базисные векторы преобразуются в обратном направлении, т. е. с обратным преобразованием $T^{-1}$ . ^[4] Это дает новую систему координат XYZ с базисными векторами: $\mathbf {e} _{X}=T^{-1}(1,0,0),\ \mathbf {e} _{Y}=T^{-1}(0,1,0),\ \mathbf {e} _{Z}=T^{-1}(0,0,1)$

Новые координаты $(v_{X},v_{Y},v_{Z})$ из $\mathbf {v}$ относительно новой системы координат XYZ определяются как: $\mathbf {v} =(v_{x},v_{y},v_{z})=v_{X}\mathbf {e} _{X}+v_{Y}\mathbf {e} _{Y}+v_{Z}\mathbf {e} _{Z}=T^{-1}(v_{X},v_{Y},v_{Z}).$

Из этого уравнения видно, что новые координаты определяются выражением $(v_{X},v_{Y},v_{Z})=T(v_{x},v_{y},v_{z}).$

Как пассивное преобразование $T$ преобразует старые координаты в новые.

Обратите внимание на эквивалентность двух видов преобразований: координаты новой точки в активном преобразовании и новые координаты точки в пассивном преобразовании одинаковы, а именно $(v_{X},v_{Y},v_{Z})=(v'_{x},v'_{y},v'_{z}).$

В абстрактных векторных пространствах [ править ]

Различие между активными и пассивными преобразованиями можно увидеть математически, рассматривая абстрактные векторные пространства .

Зафиксируйте конечномерное векторное пространство $V$ над полем $K$ (думал как $\mathbb {R}$ или $\mathbb {C}$ ), и основа ${\mathcal {B}}=\{e_{i}\}_{1\leq i\leq n}$ из $V$ . Этот базис обеспечивает изоморфизм $C:K^{n}\rightarrow V$ через карту компонентов ${\textstyle (v_{i})_{1\leq i\leq n}=(v_{1},\cdots ,v_{n})\mapsto \sum _{i}v_{i}e_{i}}$ .

Тогда активное преобразование является эндоморфизмом на $V$ , то есть линейное отображение из $V$ самому себе. Принимая такое преобразование $\tau \in {\text{End}}(V)$ , вектор $v\in V$ трансформируется как $v\mapsto \tau v$ . Компоненты $\tau$ по отношению к основе ${\mathcal {B}}$ определяются через уравнение ${\textstyle \tau e_{i}=\sum _{j}\tau _{ji}e_{j}}$ . Тогда компоненты $v$ трансформировать как $v_{i}\mapsto \tau _{ij}v_{j}$ .

Пассивное преобразование вместо этого является эндоморфизмом на $K^{n}$ . Это относится к компонентам: $v_{i}\mapsto T_{ij}v_{j}=:v'_{i}$ . При условии, что $T$ обратим, новый базис ${\mathcal {B}}'=\{e'_{i}\}$ определяется, спрашивая, что $v_{i}e_{i}=v'_{i}e'_{i}$ , откуда выражение $e'_{i}=(T^{-1})_{ji}e_{j}$ можно вывести.

Хотя пространства ${\text{End}}(V)$ и ${\text{End}}({K^{n}})$ изоморфны, они не канонически изоморфны. Тем не менее выбор основы ${\mathcal {B}}$ позволяет построить изоморфизм.

Как действия влево и вправо [ править ]

Часто ограничиваются случаем, когда отображения обратимы, так что активные преобразования представляют собой общую линейную группу. ${\text{GL}}(V)$ преобразований, тогда как пассивные преобразования представляют собой группу ${\text{GL}}(n,K)$ .

Тогда преобразования можно понимать как действие в пространстве базисов для $V$ . Активная трансформация $\tau \in {\text{GL}}(V)$ отправляет основу $\{e_{i}\}\mapsto \{\tau e_{i}\}$ . При этом пассивное преобразование $T\in {\text{GL}}(n,K)$ отправляет основу ${\textstyle \{e_{i}\}\mapsto \left\{\sum _{j}(T^{-1})_{ji}e_{j}\right\}}$ .

Обратное к пассивному преобразованию гарантирует, что компоненты преобразуются одинаково при $\tau$ и $T$ . Таким образом, это дает резкое различие между активными и пассивными преобразованиями: активные преобразования действуют слева на основаниях, а пассивные преобразования действуют справа из-за обратного.

Это наблюдение становится более естественным при просмотре баз ${\mathcal {B}}$ как выбор изоморфизма $\Phi _{\mathcal {B}}:V\rightarrow K^{n}$ . Пространство базисов эквивалентно пространству таких изоморфизмов, обозначаемому ${\text{Iso}}(V,K^{n})$ . Активные преобразования, отождествляемые с ${\text{GL}}(V)$ , действовать дальше ${\text{Iso}}(V,K^{n})$ слева по композиции, а пассивные трансформации, отождествляемые с ${\text{GL}}(n,K)$ действует на ${\text{Iso}}(V,K^{n})$ справа по предварительному составу.

Это превращает пространство оснований в левое. ${\text{GL}}(V)$ - торсор и правая ${\text{GL}}(n,K)$ -торсор.

С физической точки зрения активные преобразования можно охарактеризовать как преобразования физического пространства, тогда как пассивные преобразования характеризуются как избыточность в описании физического пространства. Это играет важную роль в математической калибровочной теории , где калибровочные преобразования математически описываются картами переходов, действующими справа на слоях.

См. также [ править ]

Ссылки [ править ]

^ Крампин, М.; Пирани, ФАЭ (1986). Применимая дифференциальная геометрия . Издательство Кембриджского университета. п. 22.
^ Jump up to: Перейти обратно: ^а ^б Джозеф К. Дэвидсон, Кеннет Хендерсон Хант (2004). «§4.4.1 Активная интерпретация и активное преобразование» . Роботы и теория винтов: приложения кинематики и статики в робототехнике . Издательство Оксфордского университета. п. 74 и далее . ISBN 0-19-856245-4 .
^ Баргманн, Валентин (1957). «Относительность». Обзоры современной физики . 29 (2): 161–174. дои : 10.1103/RevModPhys.29.161 .
^ Амидрор, Исаак (2007). «Приложение D: Замечание D.12» . Теория явления Муара: Апериодические слои . Спрингер. п. 346. ИСБН 978-1-4020-5457-0 .

Дирк Струик (1953) Лекции по аналитической и проективной геометрии , стр. 84, Аддисон-Уэсли .

Внешние ссылки [ править ]

Неоднозначность пользовательского интерфейса

[1] Крампин, М.; Пирани, ФАЭ (1986). Применимая дифференциальная геометрия . Издательство Кембриджского университета. п. 22.

[Davidson-2] Jump up to: Перейти обратно: ^а ^б Джозеф К. Дэвидсон, Кеннет Хендерсон Хант (2004). «§4.4.1 Активная интерпретация и активное преобразование» . Роботы и теория винтов: приложения кинематики и статики в робототехнике . Издательство Оксфордского университета. п. 74 и далее . ISBN 0-19-856245-4 .

[3] Баргманн, Валентин (1957). «Относительность». Обзоры современной физики . 29 (2): 161–174. дои : 10.1103/RevModPhys.29.161 .

[Amidror-4] Амидрор, Исаак (2007). «Приложение D: Замечание D.12» . Теория явления Муара: Апериодические слои . Спрингер. п. 346. ИСБН 978-1-4020-5457-0 .

[1]

[2]

[3]

[4]