Код Грея

	Лукальный код ^{[ 1 ]}^{[ 2 ]}
	5	4	3	2	1
	Код Грея
	4	3	2	1
0	0	0	0	0	0
1	0	0	0	1	1
2	0	0	1	1	0
3	0	0	1	0	1
4	0	1	1	0	0
5	0	1	1	1	1
6	0	1	0	1	0
7	0	1	0	0	1
8	1	1	0	0	0
9	1	1	0	1	1
10	1	1	1	1	0
11	1	1	1	0	1
12	1	0	1	0	0
13	1	0	1	1	1
14	1	0	0	1	0
15	1	0	0	0	1

Отраженный двоичный код ( RBC ), также известный как отраженный двоичный код ( RB ) или код Грея в честь Фрэнка Грея , представляет собой такой порядок двоичной системы счисления , при котором два последовательных значения отличаются только одним битом (двоичной цифрой).

Например, представление десятичного значения «1» в двоичном формате обычно будет выглядеть так: « 001 " и "2" будут " 010 ». В коде Грея эти значения представлены как « 001 "и" 011 ". Таким образом, для увеличения значения от 1 до 2 требуется изменить только один бит вместо двух.

Коды Грея широко используются для предотвращения ложных выходных сигналов электромеханических переключателей и для облегчения исправления ошибок в цифровой связи, такой как цифровое наземное телевидение и некоторые кабельного телевидения системы . Использование кода Грея в этих устройствах помогает упростить логические операции и уменьшить количество ошибок на практике. ^{[ 3 ]}

Функция

Многие устройства указывают положение замыканием и размыканием переключателей. Если это устройство использует естественные двоичные коды , позиции 3 и 4 находятся рядом друг с другом, но все три бита двоичного представления различаются:

Десятичный	Двоичный
...	...
3	011
4	100
...	...

Проблема с естественными двоичными кодами заключается в том, что физические переключатели не идеальны: маловероятно, что физические переключатели будут менять состояния точно синхронно. При переходе между двумя состояниями, показанными выше, все три переключателя меняют состояние. В течение короткого периода времени, пока все меняется, переключатели будут показывать какое-то ложное положение. Даже без нажатия клавиш переход может выглядеть так: 011 — 001 — 101 — 100 . Когда кажется, что переключатели находятся в положении 001 наблюдатель не может определить, является ли это «реальной» позицией 1 или переходным состоянием между двумя другими позициями. Если выходные данные подаются в последовательную систему, возможно, через комбинационную логику , то последовательная система может сохранить ложное значение.

Эту проблему можно решить, меняя только один переключатель за раз, чтобы никогда не было никакой двусмысленности положения, в результате чего коды присваивали каждому из непрерывного набора целых чисел или каждому члену циклического списка слово символов, такое как что не существует двух одинаковых кодовых слов и каждые два соседних кодовых слова отличаются ровно на один символ. Эти коды также известны как единичное расстояние . ^{[ 4 ]}^{[ 5 ]}^{[ 6 ]}^{[ 7 ]}^{[ 8 ]} однодистанционный , одношаговый , монострофический ^{[ 9 ]}^{[ 10 ]}^{[ 7 ]}^{[ 8 ]} или синкопические коды , ^{[ 9 ]} относительно расстояния Хэмминга , равного 1, между соседними кодами.

Изобретение

В принципе, для заданной длины слова может быть более одного такого кода, но термин «код Грея» впервые был применен к конкретному двоичному коду для неотрицательных целых чисел, коду Грея с двоичным отражением или BRGC . Bell Labs Исследователь Джордж Р. Стибиц описал такой код в заявке на патент 1941 года, выданной в 1943 году. ^{[ 11 ]}^{[ 12 ]}^{[ 13 ]} Фрэнк Грей ввел термин « отраженный двоичный код» в своей заявке на патент 1947 года, отметив, что этот код «пока не имеет признанного названия». ^{[ 14 ]} Он получил это название из-за того, что он «может быть создан из обычного двоичного кода посредством своего рода процесса отражения».

В стандартной кодировке кода Грея младший бит следует повторяющейся схеме: 2 включено, 2 выключено (… 11001100 … ); следующая цифра по схеме: 4 включено, 4 выключено; - й i наименее значащий бит - шаблон из 2 ^я на 2 ^я выключенный. Старшая значащая цифра является исключением из этого правила: для n -битного кода Грея самая значащая цифра соответствует шаблону 2. ^{п -1} да, 2 ^{п -1} выключено, что представляет собой ту же (циклическую) последовательность значений, что и для второй по значимости цифры, но сдвинутую вперед на 2 ^{п -2} места. Четырехбитная версия этого показана ниже:

Десятичный	Двоичный	Серый
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
5	0101	0111
6	0110	0101
7	0111	0100
8	1000	1100
9	1001	1101
10	1010	1111
11	1011	1110
12	1100	1010
13	1101	1011
14	1110	1001
15	1111	1000

Для десятичного числа 15 код переходит в десятичное 0 всего лишь одним переключением переключателя. Это называется свойством цикличности или смежности кода. ^{[ 15 ]}

В современной цифровой связи коды Грея играют важную роль в исправлении ошибок . Например, в схеме цифровой модуляции , такой как QAM , где данные обычно передаются в символах сигнала длиной 4 или более бит, диаграмма созвездия устроена так, что комбинации битов, передаваемые соседними точками созвездия, отличаются только на один бит. Комбинируя это с прямой коррекцией ошибок , способной исправлять однобитовые ошибки, приемник может исправлять любые ошибки передачи, которые вызывают отклонение точки совокупности в область соседней точки. Это делает систему передачи менее восприимчивой к шуму .

Несмотря на то, что Стибиц описал этот код ^{[ 11 ]}^{[ 12 ]}^{[ 13 ]} до Грея отраженный двоичный код позже был назван в честь Грея другими, кто его использовал. В двух разных патентных заявках 1953 года «код Грея» используется в качестве альтернативного названия «отраженного двоичного кода»; ^{[ 16 ]}^{[ 17 ]} в одном из них среди названий также указаны «минимальный код ошибки» и «код циклической перестановки». ^{[ 17 ]} В патентной заявке 1954 года упоминается «код Bell Telephone Grey». ^{[ 18 ]} Другие названия включают «циклический двоичный код», ^{[ 12 ]} «циклический код прогрессии», ^{[ 19 ]}^{[ 12 ]} «циклический перестановочный двоичный файл» ^{[ 20 ]} или «циклический перестановочный двоичный файл» (CPB). ^{[ 21 ]}^{[ 22 ]}

Код Грея иногда ошибочно приписывают изобретателю электрических устройств 19-го века Элише Грею . ^{[ 13 ]}^{[ 23 ]}^{[ 24 ]}^{[ 25 ]}

История и практическое применение

Математические головоломки

Отраженные двоичные коды применялись для решения математических задач еще до того, как они стали известны инженерам.

Двоично отраженный код Грея представляет собой основную схему классической китайской головоломки с кольцами — последовательного механического механизма головоломки, описанного французом Луи Гро в 1872 году. ^{[ 26 ]}^{[ 13 ]}

Он может служить руководством по решению проблемы Ханойских башен , основанной на игре француза Эдуарда Лукаса 1883 года. ^{[ 27 ]}^{[ 28 ]}^{[ 29 ]}^{[ 30 ]} Аналогично, так называемые игровые конфигурации «Башни Бухареста» и «Башни Клагенфурта» дают троичные и пентарные коды Грея. ^{[ 31 ]}

Мартин Гарднер написал популярный отчет о коде Грея в своей колонке «Математические игры» в журнале Scientific American в августе 1972 года . ^{[ 32 ]}

Код также образует гамильтонов цикл на гиперкубе , где каждый бит рассматривается как одно измерение.

Телеграфные коды

Когда в 1875 году французский инженер Эмиль Бодо перешел с использования 6-значного (6-битного) кода на 5-значный код для своей печатной телеграфной системы. ^{[ 33 ]} или 1876 год, ^{[ 34 ]}^{[ 35 ]} он упорядочил алфавитные символы на своем печатном колесе, используя отраженный двоичный код, и присвоил коды, используя только три бита, гласным. Гласные и согласные отсортированы в алфавитном порядке. ^{[ 36 ]}^{[ 37 ]}^{[ 38 ]} и другие символы, размещенные соответствующим образом, 5-битовый код символа был распознан как отраженный двоичный код. ^{[ 13 ]} Этот код стал известен как код Бодо. ^{[ 39 ]} и, с небольшими изменениями, в конечном итоге был принят в качестве Международного телеграфного алфавита № 1 (ITA1, CCITT-1) в 1932 году. ^{[ 40 ]}^{[ 41 ]}^{[ 38 ]}

Примерно в то же время немецко-австрийский Отто Шеффлер [ де ] ^{[ 42 ]} продемонстрировал еще один печатный телеграф в Вене, используя для той же цели 5-битный отраженный двоичный код, в 1874 году. ^{[ 43 ]}^{[ 13 ]}

Преобразование аналого-цифрового сигнала

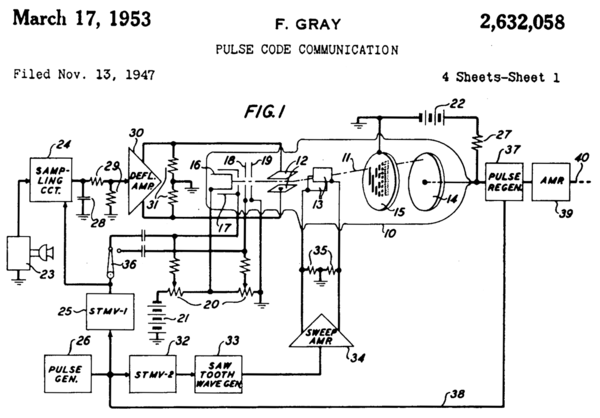
Фрэнк Грей , который прославился изобретением метода передачи сигналов, который стал использоваться для совместимого цветного телевидения, изобрел метод преобразования аналоговых сигналов в отраженные группы двоичного кода с использованием устройств на основе электронных ламп . Заявленный в 1947 году метод и устройство получили патент в 1953 году. ^{[ 14 ]} и имя Грея закрепилось за кодами. Аппарат « PCM-трубка », запатентованный Греем, был создан Рэймондом В. Сирсом из Bell Labs в сотрудничестве с Греем и Уильямом М. Гудоллом, которые приписывали Грею идею отраженного двоичного кода. ^{[ 44 ]}

Грея больше всего интересовало использование кодов для минимизации ошибок при преобразовании аналоговых сигналов в цифровые; его коды до сих пор используются для этой цели.

Датчики положения

Коды Грея используются в линейных и поворотных энкодерах положения ( абсолютных и квадратурных энкодерах ) вместо взвешенного двоичного кодирования. Это позволяет избежать возможности того, что при изменении нескольких битов в двоичном представлении позиции произойдет неправильное считывание из-за того, что некоторые биты изменятся раньше других.

Например, некоторые поворотные энкодеры имеют диск, на концентрических кольцах (дорожках) которого нанесен электропроводящий код Грея. Каждая дорожка имеет неподвижный металлический пружинный контакт, который обеспечивает электрический контакт с проводящим кодовым узором. Вместе эти контакты выдают выходные сигналы в виде кода Грея. Другие кодеры используют бесконтактные механизмы на основе оптических или магнитных датчиков для создания выходных сигналов кода Грея.

Независимо от механизма или точности движущегося энкодера, ошибка измерения положения может возникать в определенных позициях (на границах кода), поскольку код может меняться именно в тот момент, когда он считывается (выбирается). Двоичный выходной код может вызвать значительные ошибки измерения положения, поскольку невозможно изменить все биты одновременно. Если в момент выборки позиции некоторые биты изменились, а другие нет, позиция выборки будет неверной. В случае абсолютных энкодеров указанное положение может находиться далеко от фактического положения, а в случае инкрементных энкодеров это может испортить отслеживание положения.

Напротив, код Грея, используемый энкодерами положения, гарантирует, что коды для любых двух последовательных позиций будут отличаться только на один бит и, следовательно, только один бит может измениться одновременно. В этом случае максимальная ошибка положения будет небольшой, указывая на положение, смежное с фактическим положением.

Генетические алгоритмы

Из-за свойств расстояния Хэмминга кодов Грея их иногда используют в генетических алгоритмах . ^{[ 15 ]} Они очень полезны в этой области, поскольку мутации в коде допускают в основном постепенные изменения, но иногда одно битовое изменение может вызвать большой скачок и привести к появлению новых свойств.

Минимизация логической схемы

Коды Грея также используются для обозначения осей карт Карно с 1953 года. ^{[ 45 ]}^{[ 46 ]}^{[ 47 ]} а также в круговых графах Хендлера с 1958 года, ^{[ 48 ]}^{[ 49 ]}^{[ 50 ]}^{[ 51 ]} оба графических метода минимизации логических схем .

Исправление ошибок

В современной цифровой связи коды 1D- и 2D-Gray играют важную роль в предотвращении ошибок перед применением исправления ошибок . Например, в схеме цифровой модуляции , такой как QAM , где данные обычно передаются в символах сигнала длиной 4 или более бит, диаграмма созвездия устроена так, что комбинации битов, передаваемые соседними точками созвездия, отличаются только на один бит. Комбинируя это с прямой коррекцией ошибок , способной исправлять однобитовые ошибки, приемник может исправлять любые ошибки передачи, которые вызывают отклонение точки совокупности в область соседней точки. Это делает систему передачи менее восприимчивой к шуму .

Коды 4-ПСК
Коды 8-ПСК
Коды 16-КАМ

Связь между тактовыми доменами

Разработчики цифровой логики широко используют коды Грея для передачи многобитной информации между синхронными логиками, работающими на разных тактовых частотах. Считается, что логика работает в разных «тактовых доменах». Это имеет основополагающее значение для проектирования больших микросхем, работающих на разных тактовых частотах.

Переключение состояний с минимальными усилиями

Если системе приходится последовательно проходить через все возможные комбинации состояний включения-выключения некоторого набора органов управления, а изменения органов управления требуют нетривиальных затрат (например, времени, износа, человеческого труда), код Грея минимизирует количество установка изменений только на одно изменение для каждой комбинации состояний. Примером может служить тестирование системы трубопроводов на предмет всех комбинаций настроек клапанов с ручным управлением.

сбалансированный код Грея , Можно построить ^{[ 52 ]} это переворачивает каждый бит одинаково часто. Поскольку перевороты битов распределены равномерно, это оптимально следующим образом: сбалансированные коды Грея минимизируют максимальное количество переворотов битов для каждой цифры.

Счетчики кода Грея и арифметика

Джордж Р. Стибиц использовал отраженный двоичный код в устройстве счета двоичных импульсов еще в 1941 году. ^{[ 11 ]}^{[ 12 ]}^{[ 13 ]}

Типичное использование счетчиков кода Грея — это создание буфера данных FIFO (первым поступил — первым обслужен), который имеет порты чтения и записи, существующие в разных тактовых доменах. Счетчики ввода и вывода внутри такого двухпортового FIFO часто хранятся с использованием кода Грея, чтобы предотвратить захват недопустимых переходных состояний, когда счетчик пересекает домены тактовой частоты. ^{[ 53 ]} Обновленные указатели чтения и записи необходимо передавать между доменами часов при их изменении, чтобы иметь возможность отслеживать состояние пустого и полного FIFO в каждом домене. Для этой передачи в тактовой области каждый бит указателей отбирается недетерминированно. Таким образом, для каждого бита распространяется либо старое значение, либо новое значение. Следовательно, если в точке выборки изменяется более одного бита многобитового указателя, может распространяться «неправильное» двоичное значение (ни новое, ни старое). Гарантируя, что может изменяться только один бит, коды Грея гарантируют, что единственными возможными выборочными значениями являются новые или старые многобитовые значения. Обычно используются коды Грея длиной степени двойки.

Иногда цифровые шины в электронных системах используются для передачи величин, которые могут увеличиваться или уменьшаться только на единицу, например, выходные данные счетчика событий, которые передаются между доменами тактовой частоты или в цифро-аналоговый преобразователь. Преимущество кодов Грея в этих приложениях заключается в том, что различия в задержках распространения по многим проводам, представляющим биты кода, не могут привести к тому, что полученное значение пройдет через состояния, выходящие за пределы последовательности кода Грея. Это похоже на преимущество кодов Грея в конструкции механических энкодеров, однако источником кода Грея в данном случае является электронный счетчик. Сам счетчик должен считать в коде Грея, или, если счетчик работает в двоичном формате, выходное значение счетчика должно быть повторно тактировано после его преобразования в код Грея, поскольку, когда значение преобразуется из двоичного кода в код Грея, ^{[ номер 1 ]} возможно, что различия во времени поступления битов двоичных данных в схему преобразования двоичного кода в серый будут означать, что код может на короткое время проходить через состояния, которые сильно отличаются от последовательности. Добавление тактируемого регистра после схемы, которая преобразует значение счетчика в код Грея, может привести к задержке тактового цикла, поэтому подсчет непосредственно в коде Грея может быть выгодным. ^{[ 54 ]}

Чтобы получить следующее значение счетчика в счетчике кода Грея, необходимо иметь некоторую комбинационную логику, которая будет увеличивать текущее сохраненное значение счетчика. Один из способов увеличить число кода Грея — преобразовать его в обычный двоичный код. ^{[ 55 ]} добавьте к нему единицу с помощью стандартного двоичного сумматора, а затем преобразуйте результат обратно в код Грея. ^{[ 56 ]} Другие методы подсчета в коде Грея обсуждаются в отчете Роберта У. Дорана , включая получение выходных данных первых защелок главного-подчиненного триггеров в двоичном счетчике пульсаций. ^{[ 57 ]}

Адресация по коду Грея

Поскольку выполнение программного кода обычно приводит к шаблону доступа к памяти инструкций, состоящему из локально последовательных адресов, кодирование шины с использованием адресации кода Грея вместо двоичной адресации может значительно уменьшить количество изменений состояния битов адреса, тем самым снижая энергопотребление ЦП в некоторых небольших случаях. -силовые конструкции. ^{[ 58 ]}^{[ 59 ]}

Построение n- битного кода Грея

Список кодов Грея с двоичным отражением для n битов может быть сгенерирован рекурсивно из списка для n - 1 бит путем отражения списка (т. е. перечисления записей в обратном порядке), префикса записей в исходном списке двоичным кодом. 0 , добавляя к записям в отраженном списке двоичный префикс 1 , а затем объединить исходный список с обратным списком. ^{[ 13 ]} Например, создание списка n = 3 из списка n = 2:

2-битный список:	00 , 01 , 11 , 10
Отражено:		10 , 11 , 01 , 00
Префикс старых записей с 0 :	000 , 001 , 011 , 010 ,
Префикс новых записей с помощью 1 :		110 , 111 , 101 , 100
Объединено:	000 , 001 , 011 , 010 ,	110 , 111 , 101 , 100

Однобитовый код Грея: G ₁ = ( 0,1 ). Его можно рассматривать как построенный рекурсивно, как указано выше, из нуль-битового кода Грея G ₀ = ( Λ ), состоящего из одной записи нулевой длины. Этот итерационный процесс генерации G _{n +1} из G _n проясняет следующие свойства стандартного отражающего кода:

G _n — перестановка чисел 0,...,2 ^н − 1. (Каждое число появляется в списке ровно один раз.)
G _n вложен как первая половина G _{n +1} .
Следовательно, кодирование стабильно в том смысле, что, как только двоичное число появляется в G _n, оно появляется в одной и той же позиции во всех более длинных списках; поэтому имеет смысл говорить о значении отражающего кода Грея числа: G ( m ) = m -й отражающий код Грея, считая с 0.
Каждая запись в G _n отличается от предыдущей записи всего на один бит. (Расстояние Хэмминга равно 1.)
Последняя запись в G _n отличается от первой записи всего на один бит. (Код циклический.)

Эти характеристики предполагают простой и быстрый метод перевода двоичного значения в соответствующий код Грея. Каждый бит инвертируется, если следующий старший бит входного значения установлен в единицу. Это можно выполнить параллельно с помощью побитового сдвига и операции «исключающее или», если они доступны: n- й код Грея получается путем вычисления $n\oplus \left\lfloor {\tfrac {n}{2}}\right\rfloor$ . Подготовка 0 бит оставляет порядок кодовых слов неизменным, добавляя перед ним 1 бит меняет порядок кодовых слов. Если биты в позиции $i$ кодовых слов инвертируются, порядок соседних блоков $2^{i}$ кодовые слова перевернуты. Например, если бит 0 инвертируется в 3-битной последовательности кодовых слов, порядок двух соседних кодовых слов меняется на противоположный.

000 001 010 011 100 101 110 111 → 001 000 011 010 101 100 111 110 (инвертировать бит 0)

Если бит 1 инвертирован, блоки из двух кодовых слов меняют порядок:

000 001 010 011 100 101 110 111 → 010 011 000 001 110 111 100 101 (инвертировать бит 1)

Если бит 2 инвертирован, блоки из 4 кодовых слов меняются в обратном порядке:

000 001 010 011 100 101 110 111 → 100 101 110 111 000 001 010 011 (инвертировать бит 2)

Таким образом, выполняя эксклюзив или немного $b_{i}$ на позиции $i$ с битой $b_{i+1}$ на позиции $i+1$ оставляет порядок кодовых слов неизменным, если $b_{i+1}={\mathtt {0}}$ , и меняет порядок блоков $2^{i+1}$ кодовые слова, если $b_{i+1}={\mathtt {1}}$ . Это точно такая же операция, как метод отражения и префикса для генерации кода Грея.

Аналогичный метод можно использовать для выполнения обратного перевода, но вычисление каждого бита зависит от вычисленного значения следующего старшего бита, поэтому его нельзя выполнять параллельно. Предполагая $g_{i}$ это $i$ бит кода Грея ( $g_{0}$ является самым значимым битом), и $b_{i}$ это $i$ двоичный бит ( $b_{0}$ поскольку это самый старший бит), обратный перевод можно выполнить рекурсивно: $b_{0}=g_{0}$ , и $b_{i}=g_{i}\oplus b_{i-1}$ . Альтернативно, декодирование кода Грея в двоичное число можно описать как префиксную сумму битов в коде Грея, где каждая отдельная операция суммирования в сумме префикса выполняется по модулю два.

Чтобы итеративно построить бинарно-отраженный код Грея, на шаге 0 начните с $\mathrm {code} _{0}={\mathtt {0}}$ , и на шаге $i>0$ найти позицию младшего бита 1 в двоичном представлении $i$ и переверните бит в этой позиции в предыдущем коде $\mathrm {code} _{i-1}$ чтобы получить следующий код $\mathrm {code} _{i}$ . Позиции битов начинаются с 0, 1, 0, 2, 0, 1, 0, 3, .... ^{[ номер 2 ]} См. раздел «Найти первый набор», чтобы найти эффективные алгоритмы для вычисления этих значений.

Преобразование в код Грея и обратно

Следующие функции в C преобразуют двоичные числа и связанные с ними коды Грея. Хотя может показаться, что преобразование Грея в двоичный код требует обработки каждого бита по одному, существуют более быстрые алгоритмы. ^{[ 60 ]}^{[ 55 ]}^{[ номер 1 ]}

typedef unsigned int uint;

// This function converts an unsigned binary number to reflected binary Gray code.
uint BinaryToGray(uint num)
{
    return num ^ (num >> 1); // The operator >> is shift right. The operator ^ is exclusive or.
}

// This function converts a reflected binary Gray code number to a binary number.
uint GrayToBinary(uint num)
{
    uint mask = num;
    while (mask) {           // Each Gray code bit is exclusive-ored with all more significant bits.
        mask >>= 1;
        num   ^= mask;
    }
    return num;
}

// A more efficient version for Gray codes 32 bits or fewer through the use of SWAR (SIMD within a register) techniques. 
// It implements a parallel prefix XOR function. The assignment statements can be in any order.
// 
// This function can be adapted for longer Gray codes by adding steps.

uint GrayToBinary32(uint num)
{
    num ^= num >> 16;
    num ^= num >>  8;
    num ^= num >>  4;
    num ^= num >>  2;
    num ^= num >>  1;
    return num;
}
// A Four-bit-at-once variant changes a binary number (abcd)2 to (abcd)2 ^ (00ab)2, then to (abcd)2 ^ (00ab)2 ^ (0abc)2 ^ (000a)2.

На более новых процессорах количество инструкций ALU на этапе декодирования можно уменьшить, воспользовавшись набором команд CLMUL . Если MASK — это постоянная двоичная строка единиц, оканчивающаяся одной нулевой цифрой, то умножение MASK без переноса на кодировку Грея x всегда будет давать либо x, либо его побитовое отрицание.

Специальные типы кодов Грея

На практике «код Грея» почти всегда относится к коду Грея с двоичным отражением (BRGC). Однако математики открыли и другие виды кодов Грея. Как и BRGC, каждый из них состоит из списка слов, где каждое слово отличается от следующего только одной цифрой (каждое слово имеет расстояние Хэмминга 1 от следующего слова).

Коды Грея с n битами и длиной менее 2 ^н

Можно построить двоичные коды Грея с n битами длиной менее $2. н$ , если длина четная. Одна из возможностей — начать со сбалансированного кода Грея и удалить пары значений в начале и конце или в середине. ^{[ 61 ]} OEIS A290772 Последовательность ^{[ 62 ]} дает количество возможных последовательностей Грея длиной $2 n$ , которые включают ноль и используют минимальное количество битов.

n -арный код Грея

Троичное число → троичный код Грея

0 → 000
1 → 001
2 → 002
10 → 012
11 → 011
12 → 010
20 → 020
21 → 021
22 → 022
100 → 122
101 → 121
102 → 120
110 → 110
111 → 111
112 → 112
120 → 102
121 → 101
122 → 100
200 → 200
201 → 201
202 → 202
210 → 212
211 → 211
212 → 210
220 → 220
221 → 221

222 → 222

Существует множество специализированных типов кодов Грея, отличных от бинарно-отраженного кода Грея. Одним из таких типов кода Грея является n -арный код Грея , также известный как небулев код Грея . Как следует из названия, этот тип кода Грея использует . в своих кодировках нелогические значения

Например, 3-мерный ( тройной ) код Грея будет использовать значения 0,1,2. ^{[ 31 ]} ( n , k ) -код Грея представляет собой n -арный код Грея с k цифрами. ^{[ 63 ]} Последовательность элементов в коде (3, 2)-Грея: 00,01,02,12,11,10,20,21,22. ( n , k )-код Грея может быть построен рекурсивно, как BRGC, или может быть построен итеративно . -кода : Грея ( на языке Представлен алгоритм итеративной генерации (N, k) C )

// inputs: base, digits, value
// output: Gray
// Convert a value to a Gray code with the given base and digits.
// Iterating through a sequence of values would result in a sequence
// of Gray codes in which only one digit changes at a time.
void toGray(unsigned base, unsigned digits, unsigned value, unsigned gray[digits])
{ 
	unsigned baseN[digits];	// Stores the ordinary base-N number, one digit per entry
	unsigned i;		// The loop variable
 
	// Put the normal baseN number into the baseN array. For base 10, 109 
	// would be stored as [9,0,1]
	for (i = 0; i < digits; i++) {
		baseN[i] = value % base;
		value    = value / base;
	}
 
	// Convert the normal baseN number into the Gray code equivalent. Note that
	// the loop starts at the most significant digit and goes down.
	unsigned shift = 0;
	while (i--) {
		// The Gray digit gets shifted down by the sum of the higher
		// digits.
		gray[i] = (baseN[i] + shift) % base;
		shift = shift + base - gray[i];	// Subtract from base so shift is positive
	}
}
// EXAMPLES
// input: value = 1899, base = 10, digits = 4
// output: baseN[] = [9,9,8,1], gray[] = [0,1,7,1]
// input: value = 1900, base = 10, digits = 4
// output: baseN[] = [0,0,9,1], gray[] = [0,1,8,1]

Существуют и другие алгоритмы кода Грея для ( n , k )-кодов Грея. ( n , k )-код Грея, созданный вышеуказанным алгоритмом, всегда цикличен; некоторые алгоритмы, такие как алгоритм Гуана, ^{[ 63 ]} лишены этого свойства, когда k нечетно. С другой стороны, хотя с помощью этого метода за раз меняется только одна цифра, ее можно изменить путем переноса (циклического перехода от n - 1 к 0). В алгоритме Гуана счет поочередно увеличивается и уменьшается, так что числовая разница между двумя цифрами кода Грея всегда равна единице.

Коды Грея не определены однозначно, поскольку перестановка столбцов такого кода также является кодом Грея. Описанная выше процедура создает код, в котором чем ниже значение цифры, тем чаще она меняется, что делает его похожим на обычные методы счета.

См. также косую двоичную систему счисления , вариант троичной системы счисления, в которой при каждом приращении меняются не более двух цифр, поскольку каждое приращение может быть выполнено с помощью операции переноса не более одной цифры .

Сбалансированный код Грея

Хотя двоичный отраженный код Грея полезен во многих сценариях, в некоторых случаях он не оптимален из-за отсутствия «однородности». ^{[ 52 ]} В сбалансированных кодах Грея количество изменений в разных положениях координат максимально близко. Чтобы сделать это более точным, пусть G — R -арный полный цикл Грея, имеющий последовательность переходов $(\delta _{k})$ ; счетчики переходов ( спектр ) G представляют собой набор целых чисел, определяемых формулой

\lambda _{k}=|\{j\in \mathbb {Z} _{R^{n}}:\delta _{j}=k\}|\,,{\text{ for }}k\in \mathbb {Z} _{n}

Код Грея является однородным или равномерно сбалансированным , если все его счетчики переходов равны, и в этом случае мы имеем $\lambda _{k}={\tfrac {R^{n}}{n}}$ для всех к . Ясно, что когда $R=2$ , такие коды существуют только в том случае, если n — степень двойки. ^{[ 64 ]} Если n не является степенью 2, можно построить хорошо сбалансированные двоичные коды, в которых разница между двумя счетчиками переходов не превышает 2; так что (объединяя оба случая) каждый счетчик переходов либо $2\left\lfloor {\tfrac {2^{n}}{2n}}\right\rfloor$ или $2\left\lceil {\tfrac {2^{n}}{2n}}\right\rceil$ . ^{[ 52 ]} Коды Грея также могут быть экспоненциально сбалансированы , если все их счетчики переходов представляют собой смежные степени двойки, и такие коды существуют для каждой степени двойки. ^{[ 65 ]}

Например, сбалансированный 4-битный код Грея имеет 16 переходов, которые можно равномерно распределить по всем четырем позициям (четыре перехода на позицию), что делает его равномерно сбалансированным: ^{[ 52 ]}

0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0

0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0

0 0 0 0 1 1 1 1 1 0 0 1 1 1 0 0

0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1

тогда как сбалансированный 5-битный код Грея имеет всего 32 перехода, которые не могут быть равномерно распределены по позициям. В этом примере четыре позиции имеют по шесть переходов, а одна — восемь: ^{[ 52 ]}

1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0

0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 1 1 0 0 0

1 1 0 0 1 1 1 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1

1 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 1

1 1 1 1 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 1 1 1 1

Сейчас мы покажем конструкцию ^{[ 66 ]} и реализация ^{[ 67 ]} для хорошо сбалансированных двоичных кодов Грея, что позволяет нам генерировать n -разрядный сбалансированный код Грея для каждого n . Основной принцип заключается в индуктивном построении ( n + 2)-значного кода Грея. $G'$ задан n -значный код Грея G таким образом, что свойство сбалансированности сохраняется. Для этого рассмотрим разбиения $G=g_{0},\ldots ,g_{2^{n}-1}$ на четное число L непустых блоков вида

\left\{g_{0}\right\},\left\{g_{1},\ldots ,g_{k_{2}}\right\},\left\{g_{k_{2}+1},\ldots ,g_{k_{3}}\right\},\ldots ,\left\{g_{k_{L-2}+1},\ldots ,g_{-2}\right\},\left\{g_{-1}\right\}

где $k_{1}=0$ , $k_{L-1}=-2$ , и $k_{L}\equiv -1{\pmod {2^{n}}}$ ). Этот раздел вызывает $(n+2)$ -цифровой код Грея, заданный

{\mathtt {00}}g_{0},

{\mathtt {00}}g_{1},\ldots ,{\mathtt {00}}g_{k_{2}},{\mathtt {01}}g_{k_{2}},\ldots ,{\mathtt {01}}g_{1},{\mathtt {11}}g_{1},\ldots ,{\mathtt {11}}g_{k_{2}},

{\mathtt {11}}g_{k_{2}+1},\ldots ,{\mathtt {11}}g_{k_{3}},{\mathtt {01}}g_{k_{3}},\ldots ,{\mathtt {01}}g_{k_{2}+1},{\mathtt {00}}g_{k_{2}+1},\ldots ,{\mathtt {00}}g_{k_{3}},\ldots ,

{\mathtt {00}}g_{-2},{\mathtt {00}}g_{-1},{\mathtt {10}}g_{-1},{\mathtt {10}}g_{-2},\ldots ,{\mathtt {10}}g_{0},{\mathtt {11}}g_{0},{\mathtt {11}}g_{-1},{\mathtt {01}}g_{-1},{\mathtt {01}}g_{0}

Если мы определим кратности перехода

m_{i}=\left|\left\{j:\delta _{k_{j}}=i,1\leq j\leq L\right\}\right|

— это количество раз, которое цифра в позиции i меняется между последовательными блоками в разделе, тогда для ( n + 2)-значного кода Грея, индуцированного этим разделом, спектр перехода $\lambda '_{i}$ является

\lambda '_{i}={\begin{cases}4\lambda _{i}-2m_{i},&{\text{if }}0\leq i<n\\L,&{\text{ otherwise }}\end{cases}}

Тонкая часть этой конструкции состоит в том, чтобы найти адекватное разбиение сбалансированного n -разрядного кода Грея так, чтобы индуцированный им код оставался сбалансированным, но для этого имеют значение только кратности перехода; соединение двух последовательных блоков по цифре $i$ переход и разбиение другого блока на другую цифру $i$ переход создает другой код Грея с точно таким же спектром перехода $\lambda '_{i}$ , поэтому можно, например, ^{[ 65 ]} обозначить первый $m_{i}$ переходы по цифре $i$ как те, которые попадают между двумя блоками. Единые коды можно найти, когда $R\equiv 0{\pmod {4}}$ и $R^{n}\equiv 0{\pmod {n}}$ , и эту конструкцию можно распространить на R -арный случай. и ^{[ 66 ]}

Долгосрочные коды Грея

Длинный период (или максимальный промежуток ) Коды Грея максимизируют расстояние между последовательными изменениями цифр в одной и той же позиции. То есть минимальная длина любого бита остается неизменной как можно дольше. ^{[ 68 ]}

Монотонные коды Грея

Монотонные коды полезны в теории взаимосвязей сетей, особенно для минимизации расширения линейных массивов процессоров. ^{[ 69 ]} Если мы определим вес двоичной строки как количество единиц в строке, то, хотя мы явно не можем иметь код Грея со строго возрастающим весом, мы можем захотеть аппроксимировать это, пройдя код через два соседних веса, прежде чем достичь следующий.

Мы можем формализовать понятие монотонных кодов Грея следующим образом: рассмотрим разбиение гиперкуба $Q_{n}=(V_{n},E_{n})$ на уровни вершин, имеющих одинаковый вес, т.е.

V_{n}(i)=\{v\in V_{n}:v{\text{ has weight }}i\}

для $0\leq i\leq n$ . Эти уровни удовлетворяют $|V_{n}(i)|=\textstyle {\binom {n}{i}}$ . Позволять $Q_{n}(i)$ быть подграфом $Q_{n}$ вызванный $V_{n}(i)\cup V_{n}(i+1)$ , и пусть $E_{n}(i)$ быть краями в $Q_{n}(i)$ . Тогда монотонный код Грея является гамильтоновым путем в $Q_{n}$ такое, что всякий раз, когда $\delta _{1}\in E_{n}(i)$ приходит раньше $\delta _{2}\in E_{n}(j)$ в пути, тогда $i\leq j$ .

Элегантная конструкция монотонных n -значных кодов Грея для любого n основана на идее рекурсивного построения подпутей. $P_{n,j}$ длины $2\textstyle {\binom {n}{j}}$ имеющий края в $E_{n}(j)$ . ^{[ 69 ]} Мы определяем $P_{1,0}=({\mathtt {0}},{\mathtt {1}})$ , $P_{n,j}=\emptyset$ в любое время $j<0$ или $j\geq n$ , и

P_{n+1,j}={\mathtt {1}}P_{n,j-1}^{\pi _{n}},{\mathtt {0}}P_{n,j}

в противном случае. Здесь, $\pi _{n}$ является подходящим образом определенной перестановкой и $P^{\pi }$ относится к пути P с его координатами, переставленными $\pi$ . Эти пути порождают два монотонных n- значных кода Грея. $G_{n}^{(1)}$ и $G_{n}^{(2)}$ данный

G_{n}^{(1)}=P_{n,0}P_{n,1}^{R}P_{n,2}P_{n,3}^{R}\cdots {\text{ and }}G_{n}^{(2)}=P_{n,0}^{R}P_{n,1}P_{n,2}^{R}P_{n,3}\cdots

Выбор $\pi _{n}$ что гарантирует, что эти коды действительно являются кодами Грея, оказывается $\pi _{n}=E^{-1}\left(\pi _{n-1}^{2}\right)$ . Первые несколько значений $P_{n,j}$ показаны в таблице ниже.

Подпути в алгоритме Сэвиджа – Винклера
$P_{n,j}$	j = 0	j = 1	j = 2	j = 3
п = 1	0, 1
п = 2	00, 01	10, 11
п = 3	000, 001	100, 110, 010, 011	101, 111
п = 4	0000, 0001	1000, 1100, 0100, 0110, 0010, 0011	1010, 1011, 1001, 1101, 0101, 0111	1110, 1111

Эти монотонные коды Грея могут быть эффективно реализованы таким образом, что каждый последующий элемент может быть сгенерирован за время O ( n ). Алгоритм проще всего описать с помощью сопрограмм .

Монотонные коды имеют интересную связь с гипотезой Ловаса , которая утверждает, что каждый связный вершинно-транзитивный граф содержит гамильтонов путь. Подграф «среднего уровня» $Q_{2n+1}(n)$ является вершинно-транзитивным (то есть, ее группа автоморфизмов транзитивна, так что каждая вершина имеет одно и то же «локальное окружение» и не может быть отличена от других, поскольку мы можем перемаркировать координаты, а также двоичные цифры, чтобы получить автоморфизм ) и проблема поиска гамильтонова пути в этом подграфе называется «проблемой среднего уровня», которая может дать представление о более общей гипотезе. На вопрос получен положительный ответ $n\leq 15$ , а предыдущая конструкция для монотонных кодов обеспечивает гамильтонов путь длиной не менее 0,839 ‍ N , где N — количество вершин в подграфе среднего уровня. ^{[ 70 ]}

Код Беккета – Грея

Другой тип кода Грея, код Беккета-Грея , назван в честь ирландского драматурга Сэмюэля Беккета , который интересовался симметрией . В его пьесе « Квад » участвуют четыре актера, и она разделена на шестнадцать временных периодов. Каждый период заканчивается тем, что один из четырех актеров выходит на сцену или покидает ее. Спектакль начинается и заканчивается на пустой сцене, и Беккет хотел, чтобы каждая группа актеров появилась на сцене ровно один раз. ^{[ 71 ]} Очевидно, что набор актеров, находящихся в данный момент на сцене, может быть представлен 4-битным двоичным кодом Грея. Беккет, однако, наложил на сценарий дополнительное ограничение: он хотел, чтобы актеры входили и выходили, чтобы актер, который находился на сцене дольше всех, всегда уходил. Тогда актеры могут быть представлены в виде «первым пришел — первым вышел» очереди , так что (из актеров на сцене) актер, которого выводят из очереди, всегда оказывается тем, кто был поставлен в очередь первым. ^{[ 71 ]} Беккет не смог найти код Беккета–Грея для своей пьесы, и действительно, исчерпывающий список всех возможных последовательностей показывает, что такого кода не существует для n = 4. Сегодня известно, что такие коды существуют для n = 2, 5. , 6, 7 и 8 и не существуют для n = 3 или 4. Пример 8-битного кода Беккета – Грея можно найти в Дональда Кнута книге « Искусство компьютерного программирования». . ^{[ 13 ]} По мнению Савады и Вонга, пространство поиска для n более 9500 решений. = 6 можно изучить за 15 часов, и для случая n = 7 было найдено ^{[ 72 ]}

Коды «змея в коробке»

Коды «змея в коробке» , или змеи , представляют собой последовательности узлов индуцированных путей в n -мерном графе гиперкуба и коды «катушка в коробке», ^{[ 73 ]} или катушки – последовательности узлов индуцированных циклов в гиперкубе. Рассматриваемые как коды Грея, эти последовательности обладают свойством обнаруживать любую однобитовую ошибку кодирования. Коды этого типа были впервые описаны Уильямом Х. Каутцем в конце 1950-х годов; ^{[ 5 ]} с тех пор было проведено много исследований по поиску кода с максимально возможным количеством кодовых слов для данного измерения гиперкуба.

Однодорожечный код Грея

Еще один вид кода Грея — это однодорожечный код Грея (STGC), разработанный Норманом Б. Спеддингом. ^{[ 74 ]}^{[ 75 ]} и уточнен Хилтгеном, Патерсоном и Брандестини в «Однодорожечных кодах Грея» (1996). ^{[ 76 ]}^{[ 77 ]} STGC представляет собой циклический список P уникальных двоичных кодировок длины n, в которых два последовательных слова различаются ровно в одной позиции, и когда список рассматривается как P × n матрица , каждый столбец представляет собой циклический сдвиг первого столбца. ^{[ 78 ]}

Название происходит от их использования с поворотными энкодерами , где контакты распознают несколько дорожек, в результате чего на выходе каждой из них выдается 0 или 1 . Чтобы уменьшить шум из-за того, что разные контакты не переключаются в один и тот же момент времени, желательно настроить дорожки так, чтобы данные, выводимые контактами, были в коде Грея. Чтобы получить высокую угловую точность, нужно много контактов; для достижения точности не менее 1° необходимо как минимум 360 различных положений на один оборот, что требует минимум 9 бит данных и, следовательно, такого же количества контактов.

Если все контакты расположены в одинаковом угловом положении, то для получения стандартного BRGC с точностью не менее 1° необходимо 9 дорожек. Однако если производитель перемещает контакт в другое угловое положение (но на том же расстоянии от центрального вала), то соответствующий «образец колец» необходимо повернуть на тот же угол, чтобы получить тот же выходной сигнал. Если самый старший бит (внутреннее кольцо на рисунке 1) повернут достаточно, он точно соответствует следующему кольцу. Поскольку оба кольца в этом случае идентичны, внутреннее кольцо можно вырезать и датчик для этого кольца переместить на оставшееся идентичное кольцо (но со смещением под этим углом относительно другого датчика на этом кольце). Эти два датчика на одном кольце образуют квадратурный энкодер. Это уменьшает количество дорожек для углового энкодера с разрешением 1° до 8 дорожек. Еще больше сократить количество дорожек с помощью BRGC невозможно.

На протяжении многих лет Торстен Силке ^{[ 79 ]} и другие математики считали, что невозможно закодировать положение на одной дорожке так, чтобы последовательные положения различались только на одном датчике, за исключением квадратурного энкодера с 2 датчиками и 1 дорожкой. Поэтому для приложений, где 8 дорожек были слишком громоздкими, люди использовали однодорожечные инкрементальные энкодеры (квадратурные энкодеры) или 2-дорожечные энкодеры «квадратурный энкодер + эталонная метка».

Однако Норман Б. Спеддинг зарегистрировал патент в 1994 году, приведя несколько примеров, показывающих, что это возможно. ^{[ 74 ]} Хотя отличить 2 невозможно. ^н позиций с n датчиками на одном пути можно различить примерно столько же. Эцион и Патерсон предполагают, что, когда n само является степенью 2, n датчиков могут различить не более 2 ^н − 2 n позиций и что для простых n предел равен 2 ^н − 2 позиции. ^{[ 80 ]} Авторы продолжили создание 504-позиционного однодорожечного кода длиной 9, который, по их мнению, является оптимальным. Поскольку это число больше 2 ⁸ = 256, для любого кода требуется более 8 датчиков, хотя BRGC может различать 512 позиций с помощью 9 датчиков.

STGC для P = 30 и n = 5 воспроизводится здесь:

Однодорожечный код Грея на 30 позиций
Угол	Код	Угол	Код	Угол	Код	Угол	Код	Угол	Код
0°	10000	72°	01000	144°	00100	216°	00010	288°	00001
12°	10100	84°	01010	156°	00101	228°	10010	300°	01001
24°	11100	96°	01110	168°	00111	240°	10011	312°	11001
36°	11110	108°	01111	180°	10111	252°	11011	324°	11101
48°	11010	120°	01101	192°	10110	264°	01011	336°	10101
60°	11000	132°	01100	204°	00110	276°	00011	348°	10001

Каждый столбец представляет собой циклический сдвиг первого столбца, и от любой строки к следующей меняется только один бит. ^{[ 81 ]} Однопутный характер (например, кодовая цепь) полезен при изготовлении этих колес (по сравнению с BRGC), поскольку требуется только одна гусеница, что снижает их стоимость и размер. Природа кода Грея полезна (по сравнению с цепными кодами , также называемыми последовательностями Де Брейна ), поскольку в любой момент времени изменяется только один датчик, поэтому неопределенность при переходе между двумя дискретными состояниями будет составлять только плюс или минус одна единица углового отклонения. измерение, которое устройство способно разрешить. ^{[ 82 ]}

С тех пор, как был добавлен этот пример с углом 30 градусов, возник большой интерес к примерам с более высоким угловым разрешением. В 2008 году Гэри Уильямс ^{[ 83 ]} на основе предыдущей работы ^{[ 80 ]} обнаружил 9-битный однодорожечный код Грея, который дает разрешение 1 градус. Этот код Грея был использован для разработки реального устройства, которое было опубликовано на сайте Thingiverse . Это устройство ^{[ 84 ]} был разработан Эценсипом (Флориан Бауэр) в сентябре 2022 года.

STGC для P = 360 и n = 9 воспроизводится здесь:

Однодорожечный код Грея на 360 позиций
Угол	Код	Угол	Код	Угол	Код	Угол	Код	Угол	Код	Угол	Код	Угол	Код	Угол	Код	Угол	Код
0°	100000001	40°	000000011	80°	000000110	120°	000001100	160°	000011000	200°	000110000	240°	001100000	280°	011000000	320°	110000000
1°	110000001	41°	100000011	81°	000000111	121°	000001110	161°	000011100	201°	000111000	241°	001110000	281°	011100000	321°	111000000
2°	111000001	42°	110000011	82°	100000111	122°	000001111	162°	000011110	202°	000111100	242°	001111000	282°	011110000	322°	111100000
3°	111000011	43°	110000111	83°	100001111	123°	000011111	163°	000111110	203°	001111100	243°	011111000	283°	111110000	323°	111100001
4°	111000111	44°	110001111	84°	100011111	124°	000111111	164°	001111110	204°	011111100	244°	111111000	284°	111110001	324°	111100011
5°	111001111	45°	110011111	85°	100111111	125°	001111111	165°	011111110	205°	111111100	245°	111111001	285°	111110011	325°	111100111
6°	111011111	46°	110111111	86°	101111111	126°	011111111	166°	111111110	206°	111111101	246°	111111011	286°	111110111	326°	111101111
7°	111011011	47°	110110111	87°	101101111	127°	011011111	167°	110111110	207°	101111101	247°	011111011	287°	111110110	327°	111101101
8°	101011011	48°	010110111	88°	101101110	128°	011011101	168°	110111010	208°	101110101	248°	011101011	288°	111010110	328°	110101101
9°	101011111	49°	010111111	89°	101111110	129°	011111101	169°	111111010	209°	111110101	249°	111101011	289°	111010111	329°	110101111
10°	101011101	50°	010111011	90°	101110110	130°	011101101	170°	111011010	210°	110110101	250°	101101011	290°	011010111	330°	110101110
11°	101010101	51°	010101011	91°	101010110	131°	010101101	171°	101011010	211°	010110101	251°	101101010	291°	011010101	331°	110101010
12°	101010111	52°	010101111	92°	101011110	132°	010111101	172°	101111010	212°	011110101	252°	111101010	292°	111010101	332°	110101011
13°	101110111	53°	011101111	93°	111011110	133°	110111101	173°	101111011	213°	011110111	253°	111101110	293°	111011101	333°	110111011
14°	001110111	54°	011101110	94°	111011100	134°	110111001	174°	101110011	214°	011100111	254°	111001110	294°	110011101	334°	100111011
15°	001010111	55°	010101110	95°	101011100	135°	010111001	175°	101110010	215°	011100101	255°	111001010	295°	110010101	335°	100101011
16°	001011111	56°	010111110	96°	101111100	136°	011111001	176°	111110010	216°	111100101	256°	111001011	296°	110010111	336°	100101111
17°	001011011	57°	010110110	97°	101101100	137°	011011001	177°	110110010	217°	101100101	257°	011001011	297°	110010110	337°	100101101
18°	001011001	58°	010110010	98°	101100100	138°	011001001	178°	110010010	218°	100100101	258°	001001011	298°	010010110	338°	100101100
19°	001111001	59°	011110010	99°	111100100	139°	111001001	179°	110010011	219°	100100111	259°	001001111	299°	010011110	339°	100111100
20°	001111101	60°	011111010	100°	111110100	140°	111101001	180°	111010011	220°	110100111	260°	101001111	300°	010011111	340°	100111110
21°	000111101	61°	001111010	101°	011110100	141°	111101000	181°	111010001	221°	110100011	261°	101000111	301°	010001111	341°	100011110
22°	000110101	62°	001101010	102°	011010100	142°	110101000	182°	101010001	222°	010100011	262°	101000110	302°	010001101	342°	100011010
23°	000100101	63°	001001010	103°	010010100	143°	100101000	183°	001010001	223°	010100010	263°	101000100	303°	010001001	343°	100010010
24°	000101101	64°	001011010	104°	010110100	144°	101101000	184°	011010001	224°	110100010	264°	101000101	304°	010001011	344°	100010110
25°	000101001	65°	001010010	105°	010100100	145°	101001000	185°	010010001	225°	100100010	265°	001000101	305°	010001010	345°	100010100
26°	000111001	66°	001110010	106°	011100100	146°	111001000	186°	110010001	226°	100100011	266°	001000111	306°	010001110	346°	100011100
27°	000110001	67°	001100010	107°	011000100	147°	110001000	187°	100010001	227°	000100011	267°	001000110	307°	010001100	347°	100011000
28°	000010001	68°	000100010	108°	001000100	148°	010001000	188°	100010000	228°	000100001	268°	001000010	308°	010000100	348°	100001000
29°	000011001	69°	000110010	109°	001100100	149°	011001000	189°	110010000	229°	100100001	269°	001000011	309°	010000110	349°	100001100
30°	000001001	70°	000010010	110°	000100100	150°	001001000	190°	010010000	230°	100100000	270°	001000001	310°	010000010	350°	100000100
31°	100001001	71°	000010011	111°	000100110	151°	001001100	191°	010011000	231°	100110000	271°	001100001	311°	011000010	351°	110000100
32°	100001101	72°	000011011	112°	000110110	152°	001101100	192°	011011000	232°	110110000	272°	101100001	312°	011000011	352°	110000110
33°	100000101	73°	000001011	113°	000010110	153°	000101100	193°	001011000	233°	010110000	273°	101100000	313°	011000001	353°	110000010
34°	110000101	74°	100001011	114°	000010111	154°	000101110	194°	001011100	234°	010111000	274°	101110000	314°	011100001	354°	111000010
35°	010000101	75°	100001010	115°	000010101	155°	000101010	195°	001010100	235°	010101000	275°	101010000	315°	010100001	355°	101000010
36°	010000111	76°	100001110	116°	000011101	156°	000111010	196°	001110100	236°	011101000	276°	111010000	316°	110100001	356°	101000011
37°	010000011	77°	100000110	117°	000001101	157°	000011010	197°	000110100	237°	001101000	277°	011010000	317°	110100000	357°	101000001
38°	010000001	78°	100000010	118°	000000101	158°	000001010	198°	000010100	238°	000101000	278°	001010000	318°	010100000	358°	101000000
39°	000000001	79°	000000010	119°	000000100	159°	000001000	199°	000010000	239°	000100000	279°	001000000	319°	010000000	359°	100000000

Начальный и конечный углы для 20 дорожек для однопутного кода Грея с 9 датчиками, разделенными на 40°.
Начальный угол	Конечный угол	Длина
3	4	2
23	28	6
31	37	7
44	48	5
56	60	5
64	71	8
74	76	3
88	91	4
94	96	3
99	104	6
110	115	6
131	134	4
138	154	17
173	181	9
186	187	2
220	238	19
242	246	5
273	279	7
286	289	4
307	360	54

Двумерный код Грея

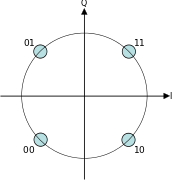
Двумерные коды Грея используются в связи для минимизации количества битовых ошибок в квадратурной амплитудной модуляции соседних точках (QAM) в созвездии . При типичном кодировании соседние точки совокупности по горизонтали и вертикали отличаются на один бит, а соседние точки по диагонали отличаются на 2 бита. ^{[ 85 ]}

Двумерные коды Грея также используются в схемах идентификации местоположения , где код будет применяться к картам территорий, таким как проекция Меркатора земной поверхности, и соответствующая циклическая двумерная функция расстояния, такая как метрика Мангейма, будет использоваться для расчета расстояние между двумя закодированными местоположениями, тем самым объединяя характеристики расстояния Хэмминга с циклическим продолжением проекции Меркатора. ^{[ 86 ]}

Превышение кода Грея

Если из этого значения извлекается часть определенного кодового значения, например, последние 3 бита 4-битного кода Грея, результирующий код будет «избыточным кодом Грея». Этот код демонстрирует свойство обратного счета извлеченных битов, если исходное значение дополнительно увеличивается. Причина этого в том, что значения, закодированные серым цветом, не демонстрируют поведение переполнения, известное из классического двоичного кодирования, при увеличении после «самого высокого» значения.

Пример. Самый высокий 3-битный код Грея, 7, кодируется как (0)100. Добавление 1 приводит к числу 8, закодированному серым цветом как 1100. Последние 3 бита не переполняются и ведут обратный отсчет, если вы еще больше увеличиваете исходный 4-битный код.

Поэтому при работе с датчиками, которые выдают несколько значений, закодированных серым цветом, последовательно, следует обратить внимание на то, выдает ли датчик эти несколько значений, закодированных в одном коде Грея, или как отдельные значения, поскольку в противном случае значения могут показаться подсчитывающимися. назад, когда ожидается «переполнение».

Серая изометрия

Биективное отображение { 0 ↔ 00 , 1 ↔ 01 , 2 ↔ 11 , 3 ↔ 10 } устанавливает изометрию между метрическим пространством над конечным полем $\mathbb {Z} _{2}^{2}$ с метрикой, заданной расстоянием Хэмминга и метрическим пространством над конечным кольцом $\mathbb {Z} _{4}$ (обычная модульная арифметика ) с метрикой, заданной расстоянием Ли . Отображение соответствующим образом расширяется до изометрии пространств Хэмминга $\mathbb {Z} _{2}^{2m}$ и $\mathbb {Z} _{4}^{m}$ . Его важность заключается в установлении соответствия между различными «хорошими», но не обязательно линейными кодами , такими как изображения карты Грея в $\mathbb {Z} _{2}^{2}$ кольцевых линейных кодов из $\mathbb {Z} _{4}$ . ^{[ 87 ]}^{[ 88 ]}

Связанные коды

Существует ряд двоичных кодов, похожих на коды Грея, в том числе:

Коды Datex, также известные как коды Джаннини (1954), как описано Карлом П. Сполдингом, ^{[ 9 ]}^{[ 89 ]}^{[ 90 ]}^{[ 91 ]}^{[ 92 ]}^{[ 8 ]} используйте вариант кода О'Брайена II .
Коды, используемые Вареком (ок. 1954 г.), ^{[ 93 ]}^{[ 94 ]}^{[ 95 ]}^{[ 96 ]} используйте вариант кода О'Брайена I, а также варианты кода Грея с основанием 12 и 16.
Лукальный кодекс (1959) ^{[ 1 ]}^{[ 2 ]}^{[ 57 ]} он же модифицированный отраженный двоичный код (MRB) ^{[ 1 ]}^{[ 2 ]}^{[ номер 3 ]}
Кодекс Гиллхэма (1961/1962), ^{[ 90 ]}^{[ 97 ]}^{[ 8 ]}^{[ 98 ]}^{[ 99 ]} использует вариант кода Datex и кода О'Брайена II .
Кодекс Лесли и Рассела (1964) ^{[ 100 ]}^{[ 10 ]}^{[ 101 ]}^{[ 97 ]}
Код учреждения Royal Radar ^{[ 97 ]}
Кодекс Хокласа (1988) ^{[ 102 ]}^{[ 103 ]}^{[ 104 ]}

Следующие двоично-десятичные коды (BCD) также являются вариантами кода Грея:

Кодекс Петерика (1953), ^{[ 19 ]}^{[ 105 ]}^{[ 106 ]}^{[ 107 ]}^{[ 55 ]}^{[ 103 ]}^{[ номер 4 ]} также известный как код Королевского авиастроительного предприятия (RAE). ^{[ 108 ]}
Коды О'Брайена I и II (1955) ^{[ 109 ]}^{[ 110 ]}^{[ 111 ]}^{[ 91 ]}^{[ 92 ]}^{[ 103 ]} (Код О'Брайена типа I ^{[ кол. 5 ]} уже был описан Фредериком А. Фоссом из IBM. ^{[ 112 ]}^{[ 113 ]} и использовался Вареком в 1954 году. Позже он был также известен как код Уоттса или отраженный десятичный код Уоттса (WRD) и иногда двусмысленно упоминается как отраженный двоичный модифицированный код Грея. ^{[ 114 ]}^{[ 20 ]}^{[ 21 ]}^{[ 115 ]}^{[ 116 ]}^{[ 117 ]}^{[ 118 ]}^{[ 119 ]}^{[ 120 ]}^{[ номер 1 ]}^{[ номер 3 ]} Код О'Брайена типа II уже использовался Datex в 1954 году. ^{[ номер 4 ]})
Код Грея Excess-3 (1956) ^{[ 121 ]} (он же код Грея превышения-3 , ^{[ 91 ]}^{[ 92 ]}^{[ 8 ]} Код Грея 3-избыток, код избытка рефлекса-3, код избытка Грея, ^{[ 103 ]} Код избытка Грея, код Грея с избытком 10-3 или код Грея-Стибитца), описанный Фрэнком П. Терви-младшим из ITT . ^{[ 121 ]}
Коды Томпкинса I и II (1956) ^{[ 4 ]}^{[ 110 ]}^{[ 111 ]}^{[ 91 ]}^{[ 92 ]}^{[ 103 ]}
Код Гликсона (1957), иногда неоднозначно называемый также модифицированным кодом Грея. ^{[ 122 ]}^{[ 55 ]}^{[ 123 ]}^{[ 124 ]}^{[ 110 ]}^{[ 111 ]}^{[ 91 ]}^{[ 92 ]}^{[ 103 ]}^{[ номер 3 ]}^{[ кол. 5 ]}

4-битные двоично-десятичные коды с единичным расстоянием ^{[ номер 6 ]}
Имя	Кусочек	0	1	2	3	4	5	6	7	8	9	Веса ^{[ номер 7 ]}	Треки	Компл.	Циклический	5 с	Комментарий

Серый BCD	4	0	0	0	0	0	0	0	0	1	1	0—3	4 (3 ^{[ номер 8 ]})	Нет	(2, 4, 8, 16)	Нет	^{[ 110 ]}^{[ 111 ]}
	3	0	0	0	0	1	1	1	1	1	1
	2	0	0	1	1	1	1	0	0	0	0
	1	0	1	1	0	0	1	1	0	0	1

Пол	4	1	0	0	0	0	0	0	0	1	1	1—3	4 (3 ^{[ номер 8 ]})	Нет	2, 10	Нет	^{[ 125 ]}
	3	0	0	0	0	1	1	1	1	1	1
	2	0	0	1	1	1	1	0	0	0	0
	1	1	1	1	0	0	1	1	0	0	1

Гликсон	4	0	0	0	0	0	0	0	0	1	1	0—3	4	Нет	2, 4, 8, 10	(сдвинуто +1)	^{[ 122 ]}^{[ 110 ]}^{[ 111 ]}^{[ 123 ]}^{[ 124 ]}^{[ кол. 5 ]}
	3	0	0	0	0	1	1	1	1	1	0
	2	0	0	1	1	1	1	0	0	0	0
	1	0	1	1	0	0	1	1	0	0	0

Томпкинс I	4	0	0	0	0	0	1	1	1	1	1	0—4	2	Нет	2, 4, 10	Да	^{[ 4 ]}^{[ 110 ]}^{[ 111 ]}
	3	0	0	0	0	1	1	1	1	1	0
	2	0	0	1	1	1	1	1	0	0	0
	1	0	1	1	0	0	0	1	1	0	0

О'Брайен I (Уоттс)	4	0	0	0	0	0	1	1	1	1	1	0—3	4	9 ^{[ 103 ]}^{[ 104 ]}^{[ номер 9 ]}	2, 4, 10	Да	^{[ 109 ]}^{[ 110 ]}^{[ 111 ]}^{[ кол. 5 ]}
	3	0	0	0	0	1	1	0	0	0	0
	2	0	0	1	1	1	1	1	1	0	0
	1	0	1	1	0	0	0	0	1	1	0

Петерик (RAE)	4	0	0	0	0	0	1	1	1	1	1	1—3	3	9 ^{[ 103 ]}^{[ 104 ]}^{[ номер 9 ]}	2, 10	Да	^{[ 19 ]}^{[ 107 ]}^{[ номер 4 ]}
	3	1	0	0	0	1	1	0	0	0	1
	2	0	0	1	1	1	1	1	1	0	0
	1	1	1	1	0	0	0	0	1	1	1

О'Брайен II	4	0	0	0	0	0	1	1	1	1	1	1—3	3	9 ^{[ 91 ]}^{[ 103 ]}^{[ 104 ]}^{[ номер 9 ]}	2, 10	Да	^{[ 109 ]}^{[ 110 ]}^{[ 111 ]}^{[ номер 4 ]}
	3	0	0	0	1	1	1	1	0	0	0
	2	0	1	1	1	0	0	1	1	1	0
	1	1	1	0	0	0	0	0	0	1	1

Зюскинд	4	0	0	0	0	0	1	1	1	1	1	1—4	3	9 ^{[ номер 9 ]}	2, 10	Да	^{[ 6 ]}
	3	0	0	1	1	1	1	1	1	0	0
	2	0	1	1	1	0	0	1	1	1	0
	1	1	1	1	0	0	0	0	1	1	1

Прозрачный	4	0	0	0	0	0	1	1	1	1	1	0—4	4 (3 ^{[ номер 8 ]})	9 ^{[ номер 9 ]}	2, 10	Да	^{[ 126 ]}^{[ 127 ]}
	3	0	0	0	1	1	1	1	0	0	0
	2	0	0	1	1	1	1	1	1	0	0
	1	0	1	1	1	0	0	1	1	1	0

Томпкинс II	4	0	0	0	0	0	1	1	1	1	1	1—3	2	9 ^{[ кол. 10 ]}	2, 10	Да	^{[ 4 ]}^{[ 110 ]}^{[ 111 ]}
	3	0	0	1	1	1	1	1	0	0	0
	2	1	1	1	0	0	0	0	0	1	1
	1	0	1	1	1	0	0	1	1	1	0

Эксцесс-3 Серый	4	0	0	0	0	0	1	1	1	1	1	1—4	4	9 ^{[ 103 ]}^{[ 104 ]}^{[ номер 9 ]}	2, 10	Да	^{[ 8 ]}^{[ 103 ]}
	3	0	1	1	1	1	1	1	1	1	0
	2	1	1	1	0	0	0	0	1	1	1
	1	0	0	1	1	0	0	1	1	0	0

См. также

Регистр сдвига с линейной обратной связью
Последовательность Де Брейна
Алгоритм Штейнхауса – Джонсона – Троттера - алгоритм, генерирующий коды Грея для факториальной системы счисления.
Код минимального расстояния
Последовательность Пруэ – Туэ – Морса , связанная с обратным кодом Грея.
Формула дрожи
Кривая Гильберта

Примечания

^ Jump up to: ^а ^б ^с Применяя простое правило инверсии , код Грея и код О'Брайена I можно перевести в чистый двоичный код 8421 и код Эйкена 2421 соответственно, чтобы облегчить арифметические операции. ^[С]
^ Последовательность 0, 1, 0, 2, 0, 1, 0, 3,… (последовательность A007814 в OEIS ).
^ Jump up to: ^а ^б ^с Существует несколько вариантов кода Грея, которые называются «модифицированными»: код Гликсона иногда называют модифицированным кодом Грея. ^[Д] Код Лукала также называют модифицированным отраженным двоичным кодом (MRB). ^[И] Код О'Брайена I или код Уоттса иногда называют отраженным двоичным модифицированным кодом Грея. ^[Ф]
^ Jump up to: ^а ^б ^с ^д Поменяв местами и инвертировав три битовые строки, код О'Брайена II и код Петерика можно преобразовать друг в друга.
^ Jump up to: ^а ^б ^с ^д Поменяв местами две пары битовых рядов, индивидуально сдвинув четыре битовых ряда и инвертировав одну из них, код Гликсона и код О'Брайена I друг в друга. можно перевести
^ Другие BCD-коды единичного расстояния включают 5-битный код Либо-Крейга, не связанный с кодом Грея , и код 1-2-1 .
^ В зависимости от целевого применения кода, веса Хэмминга кода могут быть важными свойствами, выходящими за рамки теоретико-кодовых соображений, а также по физическим причинам. В некоторых обстоятельствах состояния полного сброса и/или состояния полной установки должны быть опущены (fe, чтобы избежать условий непроводимости или короткого замыкания), может оказаться желательным, чтобы максимальный используемый вес был как можно меньшим (fe, чтобы уменьшить мощность потребление схемы считывателя) или для того, чтобы разница используемых весов была небольшой (например, для уменьшения акустического шума или колебаний тока).
^ Jump up to: ^а ^б ^с Для Грея BCD , Пола и кодов Клара количество необходимых дорожек чтения может быть уменьшено с 4 до 3, если допустима инверсия одной из средних дорожек.
^ Jump up to: ^а ^б ^с ^д ^и ^ж Для кодов О'Брайена I и II и Петерика , Сасскинда , Клара а также кодов Эксцесса-3 Грея , дополнение до 9 может быть получено путем инвертирования наиболее значимой (четвертой) двоичной цифры.
^ Для кода Томпкинса II можно дополнение до девяти получить, инвертировав первые три цифры и поменяв местами две средние двоичные цифры.

Ссылки

^ Jump up to: ^а ^б ^с Лукал, Гарольд М. (декабрь 1959 г.). «Арифметические операции для цифровых компьютеров с использованием модифицированного отраженного двоичного файла» . IRE-транзакции на электронных компьютерах . ЕС-8 (4): 449–458. дои : 10.1109/TEC.1959.5222057 . ISSN 0367-9950 . S2CID 206673385 . (10 страниц)
^ Jump up to: ^а ^б ^с Селлерс-младший, Фредерик Ф.; Сяо, Му-Юэ; Бернсон, Лерой В. (ноябрь 1968 г.). Логика обнаружения ошибок для цифровых компьютеров (1-е изд.). Нью-Йорк, США: Книжная компания McGraw-Hill . стр. 152–164. LCCN 68-16491 . OCLC 439460 .
^ Грей, Джоэл (март 2020 г.). «Понимание кода Грея: надежная система кодирования» . Graycode.ie . Раздел: Заключение . Проверено 30 июня 2023 г.
^ Jump up to: ^а ^б ^с ^д Томпкинс, Ховард Э. (сентябрь 1956 г.) [16 июля 1956]. «Двоично-десятичные коды единичного расстояния для двухпутевой коммутации» . IRE-транзакции на электронных компьютерах . Переписка. ИС-5 (3). Школа электротехники Мура , Пенсильванский университет , Филадельфия, Пенсильвания, США: 139. doi : 10.1109/TEC.1956.5219934 . ISSN 0367-9950 . Архивировано из оригинала 18 мая 2020 г. Проверено 18 мая 2020 г. (1 страница)
^ Jump up to: ^а ^б Каутц, Уильям Х. (июнь 1958 г.). «Коды проверки ошибок на единичном расстоянии». IRE-транзакции на электронных компьютерах . ИС-7 (2): 179–180. дои : 10.1109/TEC.1958.5222529 . ISSN 0367-9950 . S2CID 26649532 . (2 страницы)
^ Jump up to: ^а ^б Зюскинд, Альфред Крисс; Уорд, Джон Эрвин (28 марта 1958 г.) [1957, 1956]. «III.F. Коды единичного расстояния / VI.E.2. Отраженные двоичные коды». Написано в Кембридже, Массачусетс, США. В Зюскинде, Альфред Крисс (ред.). Замечания по методам аналого-цифрового преобразования . Книги по технологиям в области науки и техники. Том. 1 (3-е изд.). Нью-Йорк, США: Technology Press Массачусетского технологического института / John Wiley & Sons, Inc. / Chapman & Hall, Ltd., стр. 3-10–3-16 [3-13–3-16], 6-65. –6-60 [6-60]. (x+416+2 страницы) (Примечание. Содержание книги было первоначально подготовлено сотрудниками Лаборатории сервомеханизмов факультета электротехники Массачусетского технологического института для специальных летних программ, проводившихся в 1956 и 1957 годах. «Код чтения» Сасскинда " на самом деле является второстепенным вариантом показанного здесь кода, в котором две старшие битовые строки поменяны местами, чтобы лучше иллюстрировать симметрию. Кроме того, путем замены двух битовых строк местами и инвертировав одну из них, код можно перевести в код Петерика , тогда как, поменяв местами и инвертировав две битовые строки, код можно перевести в код Петерика. Код О'Брайена II .)
^ Jump up to: ^а ^б Чинал, Жан П. (январь 1973 г.). «3.3. Коды расстояний единиц». Написано в Париже, Франция. Методы проектирования цифровых систем . Перевод Престона, Алан; Саммер, Артур (1-е изд. на английском языке). Берлин, Германия: Akademie-Verlag / Springer-Verlag . п. 50. дои : 10.1007/978-3-642-86187-1 . ISBN 978-0-387-05871-9 . S2CID 60362404 . Лицензия № 202-100/542/73. Артикул №7617470(6047) ES 19 B 1/20 K 3 . Проверено 21 июня 2020 г. (xviii+506 страниц) (Примечание. Оригинальная книга на французском языке 1967 года называлась «Техника логических значений и арифметических калькуляторов», опубликованная издательством Éditions Dunod [ fr ] .)
^ Jump up to: ^а ^б ^с ^д ^и ^ж Военный справочник: энкодеры — угол вала в цифровом формате (PDF) . Министерство обороны США . 1991-09-30. МИЛ-ХДБК-231А. Архивировано (PDF) из оригинала 25 июля 2020 г. Проверено 25 июля 2020 г. (Примечание. Заменяет MIL-HDBK-231(AS) (01.07.1970).)
^ Jump up to: ^а ^б ^с Сполдинг, Карл П. (12 января 1965 г.) [09 марта 1954 г.]. «Система цифрового кодирования и перевода» (PDF) . Монровия, Калифорния, США: Datex Corporation. Патент США 3165731А . Серийный номер 415058. Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 21 января 2018 г. (28 страниц)
^ Jump up to: ^а ^б Рассел, А. (август 1964 г.). «Некоторые двоичные коды и новый пятиканальный код» . Управление (системы, контрольно-измерительные приборы, обработка данных, автоматизация, управление, включая прогресс автоматизации) . Специальные возможности. 8 (74). Лондон, Великобритания: Morgan-Grampain (Publishers) Limited: 399–404 . Проверено 22 июня 2020 г. (6 страниц)
^ Jump up to: ^а ^б ^с Стибиц, Джордж Роберт (12 января 1943 г.) [26 ноября 1941 г.]. «Двоичный счетчик» . Нью-Йорк, США: Bell Telephone Laboratories, Incorporated . Патент США 2307868 . Серийный № 420537 . Проверено 24 мая 2020 г. п. 2, правый столбец, строки 43–73: […] Более четкое представление о положении шаров после каждого импульса будет получено, если набор шаров будет представлен числом, имеющим одинаковое количество цифр, каждая из которых может иметь одно из двух произвольных значений, например 0 и 1. Если верхняя позиция называется 0, а нижняя позиция […] 1, то настройку счетчика […] можно прочитать слева направо как 0 100 000. […] Ниже приводится перевод количества полученных импульсов в эту форму двоичной записи для первых шестнадцати импульсов, полученных на первых пяти шарах […] Число импульсов […] Двоичная запись […] [1] (4 страницы )
^ Jump up to: ^а ^б ^с ^д ^и Уиндер, К. Фаррелл (октябрь 1959 г.). «Энкодеры угла вала обеспечивают высокую точность» (PDF) . Электронная промышленность . 18 (10). Компания Чилтон : 76–80. Архивировано из оригинала (PDF) 28 сентября 2020 г. Проверено 14 января 2018 г. п. 78: […] Тип кодового колеса, наиболее популярный в оптических кодировщиках, содержит шаблон циклического двоичного кода, предназначенный для создания циклической последовательности выходных сигналов «вкл-выкл». Циклический двоичный код также известен как код циклической прогрессии, отраженный двоичный код и код Грея. Этот код был разработан Г. Р. Стибитцем из Bell Telephone Laboratories и впервые был предложен для импульсно-кодовой модуляции систем Фрэнком Греем , также из BTL. Отсюда и название кода Грея. Код Грея или циклический код используется главным образом для исключения возможности ошибок при переходе кода, которые могут привести к серьезной неоднозначности. […]
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Кнут, Дональд Эрвин (12 сентября 2014 г.). «Перечисление и возврат/Генерация всех n -кортежей» . Искусство компьютерного программирования, Том 4А: Комбинаторные алгоритмы, Часть 1 . Том. 4А (1-е изд.). Аддисон-Уэсли Профессионал . стр. 442–443. ISBN 978-0-13348885-2 . (912 страниц)
^ Jump up to: ^а ^б Грей, Фрэнк (17 марта 1953 г.) [13 ноября 1947 г.]. Импульсно-кодовая связь (PDF) . Нью-Йорк, США: Bell Telephone Laboratories, Incorporated . Патент США 2632058 . Серийный номер 785697. Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 5 августа 2020 г. (13 страниц)
^ Jump up to: ^а ^б Голдберг, Дэвид Эдвард (1989). Генетические алгоритмы в поиске, оптимизации и машинном обучении (1-е изд.). Ридинг, Массачусетс, США: Аддисон-Уэсли . Бибкод : 1989gaso.book.....G .
^ Брекман, Джек (31 января 1956 г.) [31 декабря 1953 г.]. Схема кодирования (PDF) . Лонг-Бранч, Нью-Джерси, США: Министр армии США . Патент США 2733432 . Серийный номер 401738. Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 5 августа 2020 г. (8 страниц)
^ Jump up to: ^а ^б Рэгланд, граф Альберт; Шультайс-младший, Гарри Б. (11 февраля 1958 г.) [16 октября 1953 г.]. Чувствительная к направлению система управления положением с двоичным кодом (PDF) . Северный Голливуд, Калифорния, США: Bendix Aviation Corporation. Патент США 2823345 . Серийный номер 386524. Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 5 августа 2020 г. (10 страниц)
^ Домашек, Сол; Райнер, Стюарт (24 июня 1958 г.) [8 января 1954 г.]. Автоматическая система выпрямления (PDF) . Министр военно-морского флота США . Патент США 2839974 . Серийный номер 403085. Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 5 августа 2020 г. (8 страниц)
^ Jump up to: ^а ^б ^с Петерик, Эдвард Джон (октябрь 1953 г.). Циклическая прогрессивная двоично-десятичная система представления чисел (Техническое примечание MS15). Фарнборо, Великобритания: Королевское авиастроительное предприятие (RAE). (4 страницы) (Примечание. Иногда ее называют циклической двоично-десятичной системой представления чисел .)
^ Jump up to: ^а ^б Эванс, Дэвид Сильвестр (1960). Основы цифрового приборостроения (1-е изд.). Лондон, Великобритания: Hilger & Watts Ltd. Проверено 24 мая 2020 г. (39 страниц)
^ Jump up to: ^а ^б Эванс, Дэвид Сильвестр (март 1961 г.). «Глава третья: Прямое считывание с закодированных весов». Цифровые данные: их получение и обработка для анализа и управления процессами (1-е изд.). Лондон, Великобритания: Hilger & Watts Ltd / Interscience Publishers . стр. 18–23 . Проверено 24 мая 2020 г. п. 20–23: […] Расшифровка. […] Для декодирования кодов CPB или WRD можно применить простое правило инверсии. Показания верхних дорожек определяют способ трансляции нижних дорожек. Правило инверсии применяется построчно для CPB, а для WRD — десятилетие за десятилетием или построчно. Поэтому, начиная с верхнего или самого медленно меняющегося трека CPB, если результат нечетный (1), значение следующего трека должно быть инвертировано, т.е. 0 для 1 и 1 для 0. Однако, если первый трек четный (0 ), вторая дорожка остается прочитанной, т.е. 0 вместо 0 и 1 вместо 1. Опять же, если результирующее чтение второй дорожки нечетное, чтение третьей дорожки инвертируется и так далее. Когда нечетное число меняется на четное, строка ниже не инвертируется, а когда четное число меняется на нечетное, строка ниже инвертируется. Результатом применения этого правила к шаблону […] является чисто двоичный шаблон (PB) […], где каждой дорожке или цифре может быть присвоено определенное числовое значение (в данном случае 1, 2, 4, 8 и т. д.). […] Использование правила построчной инверсии в коде WRD создает шаблон [a] [ кода 1, 2, 4, 2 ], в котором цифрам снова могут быть присвоены числовые значения и суммированы десятилетие за десятилетием. Суммирование цифр может быть очень полезным, например, в системе высокоскоростного сканирования; но в системе параллельного декодирования […] обычно каждый двоичный квартет или декаду рассматривают как единое целое. Другими словами, если первая или более значимая декада нечетная, вторая декада исправляется или дополняется путем инвертирования дорожки D и т. д. Результатом является повторяющийся шаблон [исправленного кода WRD]. Этого чрезвычайно легко достичь, поскольку единственное требуемое изменение — это инверсия значения дорожки D или дополняющей цифры. […] (8+82 страницы) (Примечание. Автор вообще не упоминает Грея и называет стандартный код Грея «Циклическим перестановочным двоичным кодом» (CPB), в указателе книги он ошибочно указан как «циклический чистый двоичный код». )
^ Ньюсон, Пенсильвания (1965). Таблицы двоичного кодирования углов (1-е изд.). Управление по атомной энергии Соединенного Королевства , Исследовательская группа, Научно-исследовательский институт атомной энергии , Харвелл, Великобритания: Канцелярский офис Ее Величества . Проверено 24 мая 2020 г. (12 страниц)
^ Хит, ФГ (сентябрь 1961 г.). «Пионеры двоичного кодирования» . Журнал Института инженеров-электриков . 7 (81). Манчестерский колледж науки и технологий , технологический факультет Манчестерского университета , Манчестер, Великобритания: Институт инженерии и технологий (IET): 539–541. дои : 10.1049/jiee-3.1961.0300 . Архивировано из оригинала 28 марта 2020 г. Проверено 22 июня 2020 г. (3 страницы)
^ Каттермоул, Кеннет В. (1969). Написано в Харлоу, Эссекс, Великобритания. Принципы импульсно-кодовой модуляции (1-е изд.). Лондон, Великобритания / Нью-Йорк, США: Iliffe Books Ltd. / American Elsevier Publishing Company, Inc., стр. 245, 434. ISBN. 978-0-444-19747-4 . LCCN 78-80432 . СБН 444-19747-8 . п. 245: […] Кажется, существует некоторая путаница в атрибуции этого кода, поскольку с ним были связаны два изобретателя по имени Грей. Когда я впервые услышал это имя, я решил, что оно относится к Элише Грею , и Хит свидетельствует, что он использовал его. Многие считают, что это относится к Фрэнку Грею из Bell Telephone Laboratories , который в 1947 году впервые предложил использовать его в кодирующих трубках : его патент указан в библиографии. […] (2+448+2 страницы)
^ Эдвардс, Энтони Уильям Фэрбанк (2004). Зубчатые колеса разума: история диаграмм Венна . Балтимор, Мэриленд, США: Издательство Университета Джонса Хопкинса . стр. 48, 50. ISBN. 0-8018-7434-3 .
^ Гро, Люк-Агатон-Луи (1872). Théorie du Baguenodier par un clerc de notaire lyonnais (на французском языке) (1-е изд.). Лион, Франция: Эме Вентринье . Архивировано из оригинала 3 апреля 2017 г. Проверено 17 декабря 2020 г. [2] (2+16+4 страницы и 4 страницы в развороте) (Примечание. Этот буклет был опубликован анонимно, но известно, что его автором является Луи Гро.)
^ Лукас, Эдуард (ноябрь 1883 г.). Ханойская башня: настоящая аннамская головоломка — игра, привезенная из Тонкина профессором Н. Клаусом (из Сиама) мандарином из колледжа Ли Су Стиан! (на французском языке). Типография Поля Бусреза, Тур. (Примечание: Клаус де Сиам — анаграмма Лукаса д'Амьена, псевдонима автора Эдуарда Лукаса .)
^ де Парвиль, Анри [на французском языке] , изд. (27 декабря 1883 г.). "Ханойская башня, настоящая аннамская головоломка, игра, привезенная из Тонкина профессором Н. Клаусом (из Сиама), мандарином колледжа Ли-Су-Стиан. Действительно, головоломка, но интересная. Мы" Мы не можем лучше благодарить мандарина за его доброе намерение по отношению к мирянину, чем указывать на Ханойскую башню терпеливым людям, одержимым демоном азартных игр » . Журнал политических и литературных дебатов (обзор). Revue des Sciences (на французском языке) (изд. Matin). Париж, Франция: 1–2 [2]. ковчег:/12148/bpt6k462461g. Архивировано из оригинала 18 декабря 2020 г. Проверено 18 декабря 2020 г. (1 страница)
^ Аллардис, RE; Фрейзер, А.Ю. (февраль 1883 г.). Аллардис, Роберт Эдгар ; Фрейзер, Александр Юл (ред.). «Тур в Ханое» . Труды Эдинбургского математического общества (на английском и французском языках). 2 (5). Эдинбургское математическое общество : 50–53. дои : 10.1017/S0013091500037147 . eISSN 1464-3839 . ISSN 0013-0915 . S2CID 122159381 . [3] (4 страницы)
^ Лукас, Эдуард (1979) [1892]. Математические развлечения (на французском языке). Том. 3 (переиздание Библиотеки Альберта Бланшара). стр. 58. (Первое издание этой книги вышло посмертно.)
^ Jump up to: ^а ^б Гертер, Феликс; Роте, Гюнтер (14 ноября 2018 г.) [09 августа 2018 г., 12 августа 2017 г., 09 августа 2017 г., 22 апреля 2016 г.]. «Бесконтурное перечисление кода Грея и Бухарестская башня» (PDF) . Теоретическая информатика . 748 . Берлин, Германия: 40–54. arXiv : 1604.06707 . дои : 10.1016/j.tcs.2017.11.017 . ISSN 0304-3975 . S2CID 4014870 . Архивировано (PDF) из оригинала 16 декабря 2020 г. Проверено 16 декабря 2020 г. [4] (15/18/19/24 страниц)
^ Гарднер, Мартин (август 1972 г.). «Любопытные свойства кода Грея и как его можно использовать для решения головоломок». Научный американец . Математические игры . Том. 227, нет. 2. п. 106. (1 страница)
^ Земан, Джон; Фишер, Фердинанд, ред. (1877). «Некоторые недавние предложения по множественной телеграфии: А. Попунктная множественная телеграфия» . Политехнический журнал Динглера (на немецком языке). 226 . Аугсбург, Германия: JG Cotta'sche Buchhandlung : 499–507. Архивировано из оригинала 21 декабря 2020 г. Проверено 21 декабря 2020 г. п. ] [ ... ]
^ Бутрика, Эндрю Дж. (21 июня 1991 г.). «Бодо, Жан Морис Эмиль» . В Фрелихе, Фриц Э.; Кент, Аллен ; Холл, Кэролайн М. (ред.). Энциклопедия телекоммуникаций Фрелиха/Кента: Том 2 - От батарей к кодам - Телекоммуникации . Том. 2. Марсель Деккер Инк. / CRC Press . стр. 31–34. ISBN 0-8247-2901-3 . LCCN 90-3966 . Проверено 20 декабря 2020 г. п. 31: […] Прототип Бодо (4 года создания) был построен в 1876 году. Передатчик имел 5 клавиш, похожих на клавиши фортепиано. Сообщения передавались в специальном 5-элементном коде, разработанном Бодо […]
^ Фишер, Эрик Н. (20 июня 2000 г.). «Эволюция кодов символов, 1874–1968» . ковчег:/13960/t07x23w8s . Проверено 20 декабря 2020 г. […] В 1872 году [Бодо] начал исследования телеграфной системы, которая позволила бы нескольким операторам одновременно передавать данные по одному проводу и по мере получения передач печатать их обычными буквенными символами на полоске бумаги. Он получил патент на такую систему 17 июня 1874 года. […] Вместо переменной задержки, за которой следует одиночный импульс, система Бодо использовала одинаковые шесть единиц времени для передачи каждого символа. […] его ранний телеграф, вероятно, использовал шестизначный код […], который он приписывает Дэви в статье 1877 года. […] в 1876 году Бодо перепроектировал свое оборудование, чтобы использовать пятизначный код. Однако иногда знаки препинания и цифры по-прежнему были необходимы, поэтому он перенял у Хьюза использование двух специальных символов буквенного и цифрового пространства, которые заставляли принтер переключаться между регистрами одновременно с продвижением бумаги без печати. Пятизначный код, который он начал использовать в это время […], был структурирован так, чтобы соответствовать его клавиатуре […], которая управляла двумя единицами каждого символа с помощью переключателей, управляемых левой рукой, а остальные три единицы — правой рукой. […] [5] [6]
^ Ротен, Тимофей (25 декабря 1884 г.). «Телеграфный принтер Бодо» . Журнал Télégraphique (на французском языке). VIII/№16 (12). Берн, Швейцария: Международное бюро телеграфной администрации: 241–253 [249]. eISSN 2725-738X . ISSN 2223-1420 . ковчег:/12148/bpt6k5725454q. Архивировано из оригинала 21 декабря 2020 г. Проверено 20 декабря 2020 г.
^ Пендри, Генри Уолтер (1920) [октябрь 1919]. Написано в Лондоне, Великобритания. Телеграфная система печати Бодо (2-е изд.). Лондон, Бат, Мельбурн, Нью-Йорк: Сэр Исаак Питман и сыновья, Ltd., стр. 43–44. LCCN 21005277 . OCLC 778309351 . ОЛ 6633244М . Проверено 20 декабря 2020 г. (vii+184 страницы) (Примечание. Первое издание вышло в 1913 году.)
^ Jump up to: ^а ^б Макмиллан, Дэвид М. (27 апреля 2010 г.) [25 апреля 2010 г., 23 апреля 2010 г.]. «Коды, которые не считаются - некоторые печатные телеграфные коды как продукты своих технологий (с особым вниманием к теленаборному устройству)» . Лемур.com . Редакция 3. Минерал-Пойнт, Висконсин, США. Архивировано из оригинала 18 декабря 2020 г. Проверено 20 декабря 2020 г.
^ Написано в Лиссабоне, Португалия. Международная телеграфная конвенция Санкт-Петербурга и прилагаемые к ней правила и тарифы, Лиссабонская пересмотренная версия, 1908 г. / Выдержки из издания: Документы Лиссабонской международной телеграфной конференции (на французском языке). Берн, Швейцария: Международное бюро Телеграфного союза . 1909 [1908].
^ «Глава IX. Сигналы передачи, Статья 35. Сигналы передачи международных телеграфных алфавитов №№ 1 и 2, сигналов азбуки Морзе, аппарата Хьюза и аппарата Сименса». Написано в Мадриде, Испания. Правила телеграфной связи, прилагаемые к международной конвенции электросвязи - заключительный протокол к указанному постановлению - Мадрид, 1932 г. (PDF) (на французском языке). Берн, Швейцария: Международное бюро Телеграфного союза . 1933 [1932]. стр. 31–40 [33]. Архивировано (PDF) из оригинала 21 декабря 2020 г. Проверено 21 декабря 2020 г. (1+188 страниц) [7]
^ «Глава IX. Сигналы передачи. Статья 35. Сигналы передачи международных телеграфных алфавитов №№ 1 и 2, сигналов азбуки Морзе и сигналов приборов Хьюза и Сименса.». Регламент телеграфии, прилагаемый к Международной конвенции электросвязи - Заключительный протокол к Регламенту телеграфии - Мадрид, 1932 г. (PDF) (на английском и французском языках). Лондон, Великобритания: Главное почтовое отделение / Канцелярия Его Величества . 1933 [1932]. С. 32–40 [34]. 43-152-2 / 18693. Архивировано (PDF) из оригинала 21 декабря 2020 г. Проверено 21 декабря 2020 г. (1+2*120+26 страниц) [8]
^ Земанек, Генрих «Хайнц» Йозеф (1 декабря 1983 г.). Отто Шеффлер (1838–1928). Пионер телефона, телеграфии и перфокарт, а также строитель первой телефонной станции в Вене . Листы по истории техники (на немецком и английском языках). Том 41–43 (1979–1981) (1-е изд.). Вена, Австрия: Технический музей промышленности и торговли , Научно-исследовательский институт истории техники / Springer-Verlag . стр. 81–118. ISBN 3-21181779-4 . ISSN 0067-9127 . OCLC 952698275 .
^ Земанек, Генрих «Хайнц» Йозеф (7 июня 1976 г.). «Компьютерная предыстория и история в Центральной Европе» . Написано в Вене, Австрия. Международный семинар по управлению знаниями в области требований . AFIPS '76: Материалы национальной компьютерной конференции и выставки 7–10 июня 1976 г., июнь 1976 г. Vol. 1. Нью-Йорк, США: Американская федерация обществ обработки информации , Ассоциация вычислительной техники . стр. 15–20. дои : 10.1145/1499799.1499803 . ISBN 978-1-4503-7917-5 . S2CID 14114959 . Архивировано из оригинала 17 декабря 2020 г. Проверено 17 декабря 2020 г. п. 17: […] В 1874 году Шеффлер [ де ] изобрел еще один печатный телеграф , четверную систему, подобную Бодо , но механически более сложную. Телеграф Хьюза имел два синхронно вращающихся пальца: один в отправителе, другой в приемнике. С помощью клавиатуры, напоминающей фортепиано, оператор выбирал букву и тем самым прикасался к вращающемуся пальцу в соответствующем направлении. Поскольку принимающий палец в этот момент находился в том же направлении, получатель мог напечатать правильную букву. Печатные телеграфы Бодо и Шеффлера используют пятибитный двоичный код. ... Код Шеффлера — это отраженный двоичный код! То, что Ф. Грей запатентовал в 1953 году для PCM , Шеффлер применил в своем телеграфе в 1874 году по той же причине: надежность. Контактными пальцами он считывал на пяти камерах последовательно все комбинации; правый запускает печать. Если пальцы должны совершать минимальное количество движений, решением является отраженный двоичный код. Для Schaeffler эта идея была второстепенной. Точнее, код описан в письме сотрудника австрийской почты Йохана Н[эпомука] Тойфельхарта, вставлено туда в виде сноски и сообщает, что Шеффлер нашел код, комбинируя деревянные бруски с различными комбинациями, пока не нашел лучшее решение. Другой сотрудник Почты, Александр Вильгельм Ламберт из Линца, утверждает, что показал этот код Шеффлеру еще в 1872 году, но это утверждение неясно и не может быть проверено. […] (6 страниц)
^ Гудолл, Уильям М. (январь 1951 г.). «Телевидение с импульсно-кодовой модуляцией». Технический журнал Bell System . 30 (1): 33–49. дои : 10.1002/j.1538-7305.1951.tb01365.x . (Примечание. Представлено устно на Национальном съезде IRE, Нью-Йорк, март 1949 г.)
^ Карно, Морис (ноябрь 1953 г.) [23 апреля 1953 г., 17 марта 1953 г.]. «Метод карт для синтеза комбинационных логических схем» (PDF) . Труды Американского института инженеров-электриков, Часть I: Связь и электроника . 72 (5): 593–599. дои : 10.1109/TCE.1953.6371932 . S2CID 51636736 . Документ 53-217. Архивировано из оригинала (PDF) 16 апреля 2017 г. Проверено 16 апреля 2017 г. (Примечание. Также содержится краткий обзор Сэмюэля Х. Колдуэлла .)
^ Уэйкерли, Джон Ф. (1994). Цифровой дизайн: принципы и практика . Нью-Джерси, США: Прентис Холл . стр. 48–49, 222. ISBN. 0-13-211459-3 . (Примечание. В двух разделах страницы, взятых вместе, говорится, что K-карты помечены кодом Грея. В первом разделе говорится, что они помечены кодом, который изменяется только на один бит между записями, а во втором разделе говорится, что такой код называется Греем. код.)
^ Браун, Фрэнк Маркхэм (2012) [2003, 1990]. «3.9.2 Карты». Булево рассуждение - Логика булевых уравнений (переиздание 2-го изд.). Минеола, Нью-Йорк, США: Dover Publications, Inc., с. 49. ИСБН 978-0-486-42785-0 . п. 49: […] Карта Карно упорядочивает аргументы дискриминантов в соответствии с отраженным двоичным кодом, также называемым кодом Грея. […] (xii+291+3 страницы) 1-е издание
^ Дилер, Вольфганг (1958). Метод минимизации синтеза схем (графов минимизации) (диссертация) (на немецком языке). Потсдам, Германия: Дармштадтский технологический университет . Д 17. (73 стр.+прил.) [9]
^ Бергер, Эрих Р.; Купец, Вольфганг (1967) [1962]. Штайнбух, Карл В .; Вагнер, Зигфрид В. (ред.). Обработка сообщений в мягкой обложке (на немецком языке) (2-е изд.). Берлин, Германия: Springer-Verlag OHG . стр. 64, 1034–1035, 1036, 1038. LCCN 67-21079 . Название №. 1036. с. 64: […] Представление по дилеру является ясным , в котором все точки, пронумерованные в соответствии с кодом Грея […], располагаются в окрестностях круга. Однако для этого требуется много места. […] [ Диаграмма дилера , где все точки, пронумерованные по коду Грея , расположены на окружности, легко понятна. Однако для этого требуется много места.]
^ «Коллекция информатики Эрланген (ISER)» (на немецком языке). Эрланген, Германия: Университет Фридриха-Александра . 13 марта 2012 г. Архивировано из оригинала 16 мая 2017 г. Проверено 12 апреля 2017 г.
^ «Коллекция компьютерных наук Эрланген (ISER) – выходные данные» (на немецком языке). Эрланген, Германия: Университет Фридриха-Александра . 13 марта 2012 г. Архивировано из оригинала 26 февраля 2012 г. Проверено 15 апреля 2017 г.
^ Jump up to: ^а ^б ^с ^д ^и Бхат, Гириш С.; Сэвидж, Карла Дайан (1996). «Сбалансированные коды Грея» . Электронный журнал комбинаторики . 3 (1). дои : 10.37236/1249 .
^ Донохью, Райан (2003). «Синхронизация в цифровых логических схемах» (PDF) . Архивировано (PDF) из оригинала 15 января 2018 г. Проверено 15 января 2018 г.
^ Хюлст, Джордж Д. (6 февраля 1962 г.) [15 ноября 1957 г.]. Отраженный счетчик двоичного кода (PDF) . Натли, Нью-Джерси, США: Международная телефонная и телеграфная корпорация (ITT). Патент США 3020481 . Серийный номер 696793. Архивировано (PDF) из оригинала 6 августа 2020 г. Проверено 6 августа 2020 г. (5 страниц)
^ Jump up to: ^а ^б ^с ^д Пауэлл, Э. Александр (июнь 1968 г.). «Коды, особенно полезные для аналого-цифрового преобразования». Краткое примечание о полезных кодах для схем управления жидкостью (PDF) . Крэнфилд, Великобритания: Колледж аэронавтики , факультет технологии производства. стр. 7, 9. S2CID 215864694 . Памятка CoA 156. Архивировано (PDF) из оригинала 15 декабря 2020 г. Проверено 15 декабря 2020 г. (18 страниц) (Примечание. В статье код Гликсона называется модифицированным кодом Грея , а Ричарда В. Хэмминга написано с ошибкой.) имя
^ Мехта, Хузефа; Оуэнс, Роберт Майкл; Ирвин, Мэри Джейн «Джэни» (22 марта 1996 г.). «Некоторые проблемы с адресацией кода Грея» . Материалы шестого симпозиума Великих озер по СБИС . Компьютерное общество IEEE . стр. 178–181. дои : 10.1109/ГЛСВ.1996.497616 . ISBN 978-0-8186-7502-7 . ISSN 1066-1395 . S2CID 52837310 .
^ Jump up to: ^а ^б Доран, Роберт «Боб» Уильям (март 2007 г.). Код Грея (PDF) . Серия отчетов об исследованиях CDMTCS. Центр дискретной математики и теоретической информатики, Оклендский университет , Новая Зеландия. КДМТСС-304. Архивировано (PDF) из оригинала 22 мая 2020 г. Проверено 23 мая 2020 г. (25 страниц)
^ Су, Чинг-Лун; Цуй, Чи-Ин; Деспейн, Элвин М. (1994). Методы проектирования и компиляции архитектуры малой мощности для высокопроизводительных процессоров (PDF) (Отчет). Лаборатория передовой компьютерной архитектуры. АКАЛ-ТР-94-01. Архивировано (PDF) из оригинала 26 июля 2020 г. Проверено 17 декабря 2020 г.
^ Го, Хуэй; Парамешваран, Шри (апрель – июнь 2010 г.). «Кодировка со сдвигом Грея для уменьшения переключения шины адреса памяти команд для встраиваемых систем с низким энергопотреблением». Журнал системной архитектуры . 56 (4–6): 180–190. дои : 10.1016/j.sysarc.2010.03.003 .
^ Дитц, Генри Гордон «Хэнк» (2002). «Агрегатные магические алгоритмы: преобразование кода Грея» . Агрегат . Кафедра электротехники и вычислительной техники Инженерного колледжа Университета Кентукки . Архивировано из оригинала 16 декабря 2020 г. Проверено 16 декабря 2020 г.
^ Максфилд, Макс (29 июня 2007 г.). «Как генерировать коды Грея для последовательностей, не равных степени двойки» . Архивировано из оригинала 29 января 2022 г. Проверено 29 января 2022 г.
^ (последовательность A290772 в OEIS )
^ Jump up to: ^а ^б Гуан, Дах-Джых (1998). «Обобщенные коды Грея с приложениями». Труды Национального научного совета Китайской Республики, Часть А. 22 : 841–848. CiteSeerX 10.1.1.119.1344 .
^ Д. Г. Вагнер, Дж. Уэст (1991). «Построение унифицированных кодов Грея». Конгресс Нумерантиум . 80 : 217–223.
^ Jump up to: ^а ^б Супарта, И. Ненгах (2005). «Простое доказательство существования экспоненциально сбалансированных кодов Грея» . Электронный журнал комбинаторики . 12 . дои : 10.37236/1986 .
^ Jump up to: ^а ^б Флахайв, Мэри Элизабет ; Бозе, Белла (2007). «Балансировка циклических R -арных кодов Грея» . Электронный журнал комбинаторики . 14 . дои : 10.37236/949 .
^ Стракс, Рауль; Писсенс, Франк (2016). «Ариадна: минимальный подход к непрерывности государства» . Усеникс Безопасность . 25 .
^ Сэвидж, Карла Дайан (1997). «Обзор комбинаторных кодов Грея» . Обзор СИАМ . 39 (4). Общество промышленной и прикладной математики (SIAM): 605–629. Бибкод : 1997SIAMR..39..605S . CiteSeerX 10.1.1.39.1924 . дои : 10.1137/S0036144595295272 . JSTOR 2132693 . S2CID 6375360 .
^ Jump up to: ^а ^б Сэвидж, Карла Дайан ; Винклер, Питер (1995). «Монотонные коды Грея и проблема средних уровней» . Журнал комбинаторной теории . Серия А. 70 (2): 230–248. дои : 10.1016/0097-3165(95)90091-8 . ISSN 0097-3165 .
^ Сэвидж, Карла Дайан (16 января 1997 г.). «Длинные циклы на средних двух уровнях булевой решетки» . Арс Комбинатория . 35 (А). Государственный университет Северной Каролины, Роли, Северная Каролина, США: 97–108. CiteSeerX 10.1.1.39.2249 . ISSN 0381-7032 . S2CID 15975960 . Архивировано из оригинала 13 мая 2020 г. Проверено 13 мая 2020 г. (15 страниц)
^ Jump up to: ^а ^б Годдин, Луис (1999). «MATH 343 Дополнительные материалы по прикладной дискретной математике» (PDF) . Департамент математики Университета Саймона Фрейзера . Архивировано из оригинала (PDF) 17 февраля 2015 г.
^ Савада, Джозеф «Джо»; Вонг, Деннис Чи-Хим (2007). «Быстрый алгоритм генерации кодов Беккета – Грея». Электронные заметки по дискретной математике . 29 : 571–577. дои : 10.1016/j.endm.2007.07.091 .
^ Ричардс, Ричард Колер (январь 1971 г.). «Коды змеи в коробке». Написано в Эймсе, Айова, США. Цифровой дизайн . Нью-Йорк, США: Wiley-Interscience , John Wiley & Sons, Inc., стр. 206–207. ISBN 0-471-71945-5 . LCCN 73-147235 . (12+577+1 стр.)
^ Jump up to: ^а ^б Новая Зеландия 264738 , Спеддинг, Норман Брюс, «Кодер положения», опубликовано 28 октября 1994 г. ^{[ не удалось пройти проверку ]}
^ Спеддинг, Норман Брюс (28 октября 1994 г.). «Ниже представлена копия предварительного патента, поданного от имени Industrial Research Limited 28 октября 1994 г. – Патент Новой Зеландии 264738» (PDF) . Индустриальные Исследования Лимитед. Патент Новой Зеландии 264738. Архивировано (PDF) из оригинала 29 октября 2017 г. Проверено 14 января 2018 г.
^ Хильтген, Ален П.; Патерсон, Кеннет Г.; Брандестини, Марко (сентябрь 1996 г.). «Однодорожечные коды Грея» . Транзакции IEEE по теории информации . 42 (5): 1555–1561. дои : 10.1109/18.532900 . Збл 857.94007 .
^ Хильтген, Ален П.; Патерсон, Кеннет Г. (сентябрь 2001 г.). «Коды однопутных цепей» (PDF) . Транзакции IEEE по теории информации . 47 (6): 2587–2595. CiteSeerX 10.1.1.10.8218 . дои : 10.1109/18.945274 . Архивировано (PDF) из оригинала 15 января 2018 г. Проверено 15 января 2018 г.
^ Эцион, Туви; Шварц, Моше (ноябрь 1999 г.) [17 мая 1998 г.]. «Структура однодорожечных кодов Грея» (PDF) . Транзакции IEEE по теории информации . ИТ-45 (7): 2383–2396. CiteSeerX 10.1.1.14.8333 . дои : 10.1109/18.796379 . Архивировано (PDF) из оригинала 15 января 2018 г. Проверено 15 января 2018 г. Технический отчет CS0937. Архивировано 15 декабря 2018 г. на Wayback Machine.
^ Силке, Торстен (1997) [1993-03-01]. «Грей-коды с небольшим количеством треков (вопрос Марко Брандестини)» . Архивировано из оригинала 29 октября 2017 г. Проверено 29 октября 2017 г.
^ Jump up to: ^а ^б Эцион, Туви; Патерсон, Кеннет Г. (май 1996 г.). «Почти оптимальные однодорожечные коды Грея» (PDF) . Транзакции IEEE по теории информации . ИТ-42 (3): 779–789. CiteSeerX 10.1.1.14.1527 . дои : 10.1109/18.490544 . Архивировано (PDF) из оригинала 30 октября 2016 г. Проверено 8 апреля 2018 г.
^ Раски, Фрэнк ; Уэстон, Марк (18 июня 2005 г.). «Обзор диаграмм Венна: симметричные диаграммы» . Динамические опросы. Электронный журнал комбинаторики . дои : 10.37236/26 .
^ Альсиаторе, Дэвид Г.; Хистанд, Майкл Б. (1999). Мехатроника . Образование МакГроу – Хилла – Европа. ISBN 978-0-07-131444-2 .
^ Уильямс, Гэри (25 июля 2008 г.). « Однодорожечный код Грея предназначен для кодирования на 360 градусов с помощью 9 датчиков» . Обмен экспертами .
^ Бауэр, Флориан. «9-битный абсолютный однодорожечный поворотный энкодер с кодом Грея» . Тингиверс .
^ Кришна (11 мая 2008 г.). «Код Грея для QAM» . Архивировано из оригинала 29 октября 2017 г. Проверено 29 октября 2017 г.
^
Стрэнг, Томас; Дамманн, Армин; Рёкль, Матиас; Пласс, Саймон (октябрь 2009 г.). Использование кодов Грея в качестве идентификаторов местоположения (PDF) . 6-я экспертная дискуссия GI/ITG КуВС Геолокационные приложения и сервисы (на английском и немецком языках). Оберпфаффенхофен, Германия: Институт связи и навигации, Немецкий аэрокосмический центр (DLR). CiteSeerX 10.1.1.398.9164 . Архивировано (PDF) из оригинала 1 мая 2015 г. Проверено 16 декабря 2020 г. (5/8 страниц) [10]
- Томас Стрэнг; и др. (октябрь 2009 г.). «Использование кодов Грея в качестве идентификаторов местоположения» (PDF) . ResearchGate (Аннотация) (на немецком и английском языках). Архивировано из оригинала 03 сентября 2020 г.
^ Греферат, Маркус (2009). «Введение в теорию кольцевого линейного кодирования». В комнате, Массимилиано; Мора, Тео; Перре, Людовик; Саката, Сёдзиро; Траверсо, Карло (ред.). Базы Грёбнера, кодирование и криптография . Springer Science & Business Media . п. 220 . ISBN 978-3-540-93806-4 .
^ Соле, Патрик (2016). «Коды Кердока и Препарата» . В Хазевинкеле, Михил (ред.). Энциклопедия математики . Springer Science+Business Media . ISBN 978-1-4020-0609-8 . Архивировано из оригинала 29 октября 2017 г.
^ Сполдинг, Карл П. (12 июля 1965 г.). Как использовать энкодеры вала . Монровия, Калифорния, США: Datex Corporation. (85 страниц)
^ Jump up to: ^а ^б Уиллер, Эдвин Л. (30 декабря 1969 г.) [5 апреля 1968 г.]. Аналого-цифровой кодер (PDF) . Нью-Йорк, США: Корпорация Conrac. Патент США 3487460А . Серийный № 719026 (397812). Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 21 января 2018 г. п. 5, левый столбец 9, строки 15–22: […] Код MOA-GILLHAM по существу представляет собой комбинацию обсуждавшегося выше кода Грея и хорошо известного кода Datex ; код Datex раскрыт в патенте США 3165731 . Схема такова, что код Datex определяет биты для подсчета единиц кодера, а код Грея определяет биты для каждого из декад более высокого порядка, десятков, сотен и т. д. […] (11 страниц)
^ Jump up to: ^а ^б ^с ^д ^и ^ж Доктер, Фолкерт; Штайнхауэр, Юрген (18 июня 1973 г.). «2.4. Кодирование чисел в двоичной системе». Цифровая электроника . Техническая библиотека Philips (PTL) / Macmillan Education (переиздание 1-го изд. на английском языке). Эйндховен, Нидерланды: The Macmillan Press Ltd. / Gloeilampenfabrieken NV Philips . стр. 32, 39, 50–53. дои : 10.1007/978-1-349-01417-0 . ISBN 978-1-349-01419-4 . СБН 333-13360-9 . Проверено 11 мая 2020 г. п. 53: […] Код Datex […] использует код О'Брайена II в пределах каждого десятилетия и отражает десятичные числа для десятичных переходов. Для дальнейшей обработки необходимо преобразование кода в естественную десятичную систему счисления. Поскольку код О'Брайена II образует дополнение до девяток , это не вызывает особых трудностей: всякий раз, когда кодовое слово для десятков представляет собой нечетное число, кодовые слова для десятичных единиц задаются как дополнения до девяток путем инверсии числа. четвертая двоичная цифра. […] ^{[ постоянная мертвая ссылка ]} (270 страниц)
^ Jump up to: ^а ^б ^с ^д ^и Доктер, Фолкерт; Штайнхауэр, Юрген (1975) [1969]. «2.4.4.6. Одношаговые коды». Цифровая электроника в измерительной технике и обработке данных: Теоретические основы и схемотехника . Специализированные книги Philips (на немецком языке). Том I (улучшенное и расширенное 5-е изд.). Гамбург, Германия: Deutsche Philips GmbH . С. 41, 48, 51, 58, 60–61. ISBN 3-87145-272-6 . (xii+327+3 страницы)
^ «…точное измерение уровня жидкости – на ЛЮБОМ РАССТОЯНИИ!» . Нефтеперерабатывающий завод (Реклама). 33 (9). Gulf Publishing Company : 368. Сентябрь 1954 г. ISSN 0096-6517 . п. 368: […] Полная диспетчеризация, измерение и дистанционное управление интегрированы в одну единую систему, когда установлена система телеметрии с импульсно-кодовым кодом «Varec». […]
^ Бишуп, Бернард В.; Репета, Энтони А.; Джарриццо, Фрэнк К. (13 августа 1968 г.) [3 апреля 1963 г.]. «Система телеизмерения и диспетчерского управления, имеющая обычно непрерывные телеметрические сигналы» . Лидс и Нортруп Ко. US3397386A. [11]
^ «Формат импульса кодировщика». Руководство по установке и эксплуатации 4-проводного микропередатчика модели 1900 (PDF) . Сайпресс, Калифорния, США: Whessoe Varec, Inc. , январь 1993 г. [1991-07-01]. стр. 04-4–04-8. 33-08461. Архивировано (PDF) из оригинала 16 мая 2020 г. Проверено 16 мая 2020 г. (38 страниц) (Примечание. В позиции 5 для «Дюймов» на стр. 04–8 следует читать «0111», а не «1111».)
^ «2.2.3.3 Формат данных уровня MSP». Varec Model 1900 — 4-проводной микропередатчик (протокол BSAP — Mark/Space (MSP)) — Замечания по применению (PDF) . Эмерсон Электрик . стр. 11–14. Архивировано (PDF) из оригинала 16 мая 2020 г. Проверено 16 мая 2020 г. (vi+33 страницы)
^ Jump up to: ^а ^б ^с Вайтман, Эрик Джеффри (1972). «Глава 6. Измерение смещения» . Приборы в управлении технологическими процессами (1-е изд.). Лондон, Великобритания: Butterworth & Co (Publishers) Ltd. стр. 122–123. ISBN 0-408-70293-1 . п. 122–123: […] Другие формы кода также хорошо известны. Среди них кодекс Королевского радиолокационного учреждения ; Десятичный код лишних трех ; Код Гиллхэма , рекомендованный ИКАО для автоматической передачи данных о высоте для управления воздушным движением целей ; код Петерика и код Лесли и Рассела Национальной инженерной лаборатории . Каждый из них имеет свои преимущества и предлагается в качестве опции различными производителями кодеров. […] (12+367+5 страниц)
^ Филлипс, Дэррил (26 июля 2012 г.) [1998]. «Высота – МОДЕК ASCII» . Авионика ЭйрСпорт. Архивировано из оригинала 26 июля 2012 г.
^ Стюарт, К. (3 декабря 2010 г.). «Код авиационного Грея: объяснение кода Гиллхэма» . Пользовательские компьютерные услуги (CCS). Архивировано из оригинала 16 января 2018 г. Проверено 14 января 2018 г.
^ Лесли, Уильям «Билл» HP; Рассел, А. (1964). Циклический прогрессивный десятичный код для простого перевода в десятичные и аналоговые выходные данные (Отчет). Ист-Килбрайд, Глазго, Великобритания: Национальная инженерная лаборатория . Отчет NEL 129. (17 страниц)
^ Лесли, Уильям «Билл» HP (1974). «Работа над NC в НЭЛ» . В Кенигсбергере, Франц; Тобиас, Стивен Альберт (ред.). Материалы четырнадцатой Международной конференции по проектированию и исследованию станков, 12–14 сентября 1973 г. Макмиллан Пресс Лтд . С. 215–224 [215, 217]. дои : 10.1007/978-1-349-01921-2_30 . ISBN 978-1-34901921-2 . LCCN 73-16545 . СБН 333-14913-0 . Архивировано из оригинала 7 апреля 2022 г. Проверено 21 мая 2020 г.
^ Хоклас, Арчибальд (6 сентября 1989 г.) [29 апреля 1988 г.]. «Сканирующее устройство для цифрового измерения расстояния или угла» (PDF) (на немецком языке). VEB Schiffselektronik Йоханнес Варнке [ де ] . Патент ГДР DD271603A1. WP H 03 M / 315 194 8. Архивировано из оригинала (PDF) 18 января 2018 г. Проверено 18 января 2018 г. - через DEPATIS [ de ] . [12] [13]
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к Хоклас, Арчибальд (2005). «Код Грея – Код единичного расстояния» . Архивировано из оригинала 15 января 2018 г. Проверено 15 января 2018 г.
^ Jump up to: ^а ^б ^с ^д ^и Хоклас, Арчибальд (2005). «Код Грея – код одношаговой выборки» (на немецком языке). Архивировано из оригинала 15 января 2018 г. Проверено 15 января 2018 г.
^ Петерик, Эдвард Джон; Хопкинс, Эй Джей (1958). Некоторые недавно разработанные цифровые устройства для кодирования вращения валов (Техническая нота MS21). Фарнборо, Великобритания: Королевское авиастроительное предприятие (RAE).
^ «Дигитайзер как аналого-цифровой преобразователь в технике управления, измерения и регулирования» (PDF) . Технические уведомления . Реле, электронные устройства, органы управления (на немецком языке). Нет. 13. Кёльн-Ниль, Германия: Франц Баумгартнер (FraBa). Май 1963 г., стр. 1–2. Архивировано из оригинала (PDF) 21 мая 2020 г. Проверено 21 мая 2020 г. стр. 1-2: [...] Компания Harrison Reproduction Equipment, Фарнборо/Англия [...], за годы разработок в сотрудничестве с британскими ВВС и британскими промышленными компаниями, представила механический дигитайзер [.. .] до технической зрелости, отвечающей почти всем требованиям […], достаточно. […] Чтобы добиться четких результатов при расшифровке десятичного используемого двоичного кода и всегда получать правильные результаты при переходе от одного десятичного знака к другому в порядке, был разработан специальный код, который по своему принципу исключает всякую возможность неправильного высказываний и который также характеризуется: его структура допускает относительно легкую расшифровку. На этом основан код Петерик-Код . […] (4 страницы)
^ Jump up to: ^а ^б Чарнли, CJ; Бидгуд, RE; Бордман, GET (октябрь 1965 г.). «Конструкция пневматического энкодера положения» (PDF) . Тома трудов МФБ . 2 (3). Колледж аэронавтики, Крэнфилд, Бедфорд, Англия: 75–88. дои : 10.1016/S1474-6670(17)68955-9 . Глава 1.5 . Проверено 14 января 2018 г. ^{[ постоянная мертвая ссылка ]}
^ Холлингдейл, Стюарт Х. (19 сентября 1958 г.). «Сессия 14. Обработка данных» . Применение компьютеров (доклад конференции). Атлас – Применение компьютеров, Ноттингемский университет, 15–19 сентября 1958 г. Архивировано из оригинала 25 мая 2020 г. Проверено 25 мая 2020 г.
^ Jump up to: ^а ^б ^с О'Брайен, Джозеф А. (май 1956 г.) [15 ноября 1955 г., 23 июня 1955 г.]. «Циклические десятичные коды для аналого-цифровых преобразователей» . Труды Американского института инженеров-электриков, Часть I: Связь и электроника . 75 (2). Bell Telephone Laboratories, Уиппани, Нью-Джерси, США: 120–122. дои : 10.1109/TCE.1956.6372498 . ISSN 0097-2452 . S2CID 51657314 . Документ 56-21. Архивировано из оригинала 18 мая 2020 г. Проверено 18 мая 2020 г. (3 страницы) (Примечание. Этот документ был подготовлен для презентации на Зимнем общем собрании AIEE, Нью-Йорк, США, с 30 января 1956 г. по 3 февраля 1956 г.)
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Штайнбух, Карл В. , изд. Написано в Карлсруэ, Германия. Обработка сообщений в мягкой обложке (на немецком языке) (1-е изд.). Берлин / Геттинген / Нью-Йорк: Springer-Verlag OHG . стр. 71–74, 97, 761–764, 770, 1080–1081. LCCN 62-14511 .
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Штайнбух, Карл В .; Вебер, Вольфганг; Хайнеманн, Трауте, ред. (1974) [1967]. Карманный справочник по информатике - Том II - Структура и программирование компьютерных систем . Обработка сообщений в мягкой обложке (на немецком языке). Том 2 (3-е изд.). Берлин, Германия: Springer Verlag . стр. 98–100. ISBN 3-540-06241-6 . LCCN 73-80607 .
^ Фосс, Фредерик А. (27 декабря 1960 г.) [17 декабря 1954 г.]. «Системы управления» (PDF) . Международная Бизнес Машинная Корпорация . Рис. 7, Рис. 8, Рис. 11. Патент США 2966670А . Серийный номер 475945. Архивировано (PDF) из оригинала 21 июня 2020 г. Проверено 5 августа 2020 г. (14 страниц) (Примечание. Автор назвал свой код 2*-4-2-1 (+9-±7-±3-±1), отраженный десятичный код.)
^ Фосс, Фредерик А. (декабрь 1954 г.). «Использование отраженного кода в цифровых системах управления». IRE-транзакции на электронных компьютерах . ИК-3 (4): 1–6. дои : 10.1109/IREPGELC.1954.6499244 . ISSN 2168-1740 . (6 страниц)
^ Эванс, Дэвид Сильвестр (1958). «[название неизвестно]» . Транзакции . 10–12. Институт измерения и контроля: 87. (Примечание. Код Уоттса назывался кодом WRD или Watts Reflected Decimal, чтобы отличать его от других кодов, используемых в Hilger & Watts Ltd. )
^ Бенджамин, PW; Николлс, GS (1963). «3.2.2 Электромеханические цифровые преобразователи» . Измерение спектров нейтронов методом полуавтоматического сканирования протонов отдачи в фотоэмульсиях . Управление по атомной энергии Соединенного Королевства , Научно-исследовательский центр по атомному оружию , Великобритания: Министерство энергетики США . стр. 8–10, 19. Отчет AWRE № NR 5/63. [14] (23 страницы)
^ Клинковски, Джеймс Дж. (14 марта 1967 г.) [23 марта 1964 г.]. «Схемы электронного диодно-матричного декодера» (PDF) . Детройт, Мичиган, США: Корпорация Берроуз . Патент США 3309695А . Серийный номер 353845. Архивировано (PDF) из оригинала 23 мая 2020 г. Проверено 23 мая 2020 г. (5 страниц) [15]
^ Клинковски, Джеймс Дж. (31 марта 1970 г.) [22 декабря 1966 г.]. «Преобразователь двоично-десятичных сигналов» (PDF) . Детройт, Мичиган, США: Корпорация Берроуз . Патент США 3504363А . Серийный номер 603926. Архивировано (PDF) из оригинала 23 мая 2020 г. Проверено 23 мая 2020 г. (7 страниц)
^ «[название неизвестно]». Новости электротехнического проектирования . 12 . Издательская компания Роджерс . 1967. ISSN 0012-7515 . [16] [17]
^ Тот-Зентаи, Дьёрдьи (05.10.1979). «Некоторые проблемы углово-вращательных цифровых преобразователей» . Периодика Политехника Электротехника . 23 (3–4). Кафедра электронных технологий, Технический университет, Будапешт, Венгрия: 265–270 [266] . Проверено 23 мая 2020 г. [18] (6 страниц) (Примечание. Показывает 6-значный код Уоттса.)
^ Савард, Джон Дж. Г. (2018) [2006]. «Десятичные представления» . четырехблок . Архивировано из оригинала 16 июля 2018 г. Проверено 16 июля 2018 г.
^ Jump up to: ^а ^б Терви-младший, Фрэнк П. (29 июля 1958 г.) [17 мая 1956 г.]. «Кодер подсчета импульсов» (PDF) . Натли, Нью-Джерси, США: Международная телефонная и телеграфная корпорация . Патент США 2845617А . Серийный номер 585494. Архивировано (PDF) из оригинала 23 мая 2020 г. Проверено 23 мая 2020 г. (5 страниц)
^ Jump up to: ^а ^б Гликсон, Гарри Роберт (март 1957 г.). «Можете ли вы воспользоваться преимуществами циклического двоично-десятичного кода?» . Техника управления . 4 (3). Техническая издательская компания , подразделение издательской корпорации Dun-Donnelley, Dun & Bradstreet Corp .: 87–91. ISSN 0010-8049 . (5 страниц)
^ Jump up to: ^а ^б Боруки, Лоренц; Диттманн, Иоахим (1971) [июль 1970, 1966, осень 1965]. «2.3 Общие коды в цифровой измерительной технике». Написано в Крефельде/Карлсруэ, Германия. Технология цифровых измерений: Введение (на немецком языке) (2-е изд.). Берлин / Гейдельберг, Германия: Springer-Verlag . С. 10–23 [12–14]. дои : 10.1007/978-3-642-80560-8 . ISBN 3-540-05058-2 . LCCN 75-131547 . ISBN 978-3-642-80561-5 . (viii+252 страницы) 1-е издание (Примечание. Как и Каммерер , авторы описывают 6-битный 20-циклический код Гликсона.)
^ Jump up to: ^а ^б Каммерер, Вильгельм [на немецком языке] (май 1969 г.). «II.15. Структура: Представление информации в автомате». Написано в Йене, Германия. Во Фрюхауфе, Ганс [на немецком языке] ; Чемберлен, Вильгельм; Шредер, Курц; Винклер, Хельмут (ред.). Цифровые автоматы – теория, структура, технология, программирование . Электронные вычисления и правила (на немецком языке). Том 5 (1-е изд.). Берлин, Германия: Akademie-Verlag GmbH . п. 173. Лицензия № 202-100/416/69. Заказ № 4666 ES 20 K 3. (Примечание. Существует также второе издание 1973 года. Подобно Боруки и Диттманну , но не называя его кодом Гликсона, автор создает 20-циклический тетрадный код из кода Гликсона и вариант кода Гликсона с инвертированный старший бит.)
^ Пол, Матиас Р. (10 августа 1995 г.) [1994]. «Unterbrechungsfreier Schleifencode» [Код непрерывного цикла]. 1.02 (на немецком языке) . Проверено 11 февраля 2008 г. (Примечание. Автор назвал этот код Schleifencode (англ. «код цикла»). Он отличается от кода Грея BCD только кодированием состояния 0, что делает его циклическим кодом единичного расстояния для приложений с полным круговым вращением. Избегание всех -нулевой шаблон кода позволяет выполнять самотестирование контура и использовать линии передачи данных для бесперебойного распределения электроэнергии.)
^ Конечно, Райнер (1 февраля 1970 г.). Введение – Цифровые компьютеры Коллекция Гёшена (на немецком языке). Том 1241/1241а (1-е изд.). Берлин, Германия: Вальтер де Грюйтер и компания / GJ Göschen'sche Verlagsbuchhandlung [ de ] . п. 17. ISBN 3-11-083160-0 . . Архив-Nr. 7990709. Архивировано из оригинала 1 июня 2020 г. Проверено 13 апреля 2020 г. (205 страниц) (Примечание. Перепечатка первого издания за 2019 год доступна по ссылке ISBN 3-11002793-3 , 978-3-11002793-8 . переработанное и расширенное 4-е издание .) Также существует
^ Конечно, Райнер (1989) [1988-10-01]. компьютеры – Введение в структуру компьютерного оборудования Цифровые . Коллекция Гёшена (на немецком языке). Том 2050 (4-е переработанное изд.). Берлин, Германия: Walter de Gruyter & Co. 28. ISBN 3-11011700-2 . (320 страниц) (Примечание. Автор назвал этот код Einheitsabstandscode (англ. «код единичного расстояния»). Поменяв местами две битовые строки и инвертировав одну из них, его можно перевести в код О'Брайена II , тогда как поменяв местами и инвертировав две битовые строки, его можно перевести в код Петерика .)

Дальнейшее чтение

Ричардс, Ричард Колер (1955). Арифметические операции в цифровых вычислительных машинах (5-е изд.). Нью-Йорк, США: Д. Ван Ностранд Ко., Инк.
Ричардс, Ричард Колер (1967). Электронные цифровые компоненты и схемы . Д. Ван Ностранд Ко., Инк., стр. 490, 500–504, 510–511.
Блэк, Пол Э. (25 февраля 2004 г.). «Код Грея» . НИСТ .
Пресс, Уильям Х.; Теукольский, Саул А.; Веттерлинг, Уильям Т.; Фланнери, Брайан П. (2007). «Раздел 22.3. Коды Грея» . Численные рецепты: искусство научных вычислений (3-е изд.). Нью-Йорк, США: Издательство Кембриджского университета . ISBN 978-0-521-88068-8 . Архивировано из оригинала 11 августа 2011 г. Проверено 18 августа 2011 г.
Сэвидж, Карла Дайан (1997). «Обзор комбинаторных кодов Грея» . Обзор СИАМ . 39 (4). Общество промышленной и прикладной математики (SIAM): 605–629. Бибкод : 1997SIAMR..39..605S . CiteSeerX 10.1.1.39.1924 . дои : 10.1137/S0036144595295272 . JSTOR 2132693 . S2CID 6375360 .
Уилф, Герберт Сол (1989). «Главы 1–3». Комбинаторные алгоритмы: Обновление . Общество промышленной и прикладной математики (SIAM). ISBN 0-89871-231-9 .
Дьюар, Меган; Стивенс, Бретт (29 августа 2012 г.). Заказ блочных конструкций – коды Грея, универсальные циклы и конфигурация . Книги CMS по математике (1-е изд.). Нью-Йорк, США: Springer Science+Business Media . дои : 10.1007/978-1-4614-4325-4 . ISBN 978-1-46144324-7 . ISSN 1613-5237 .
Максфилд, Клайв «Макс» (1 октября 2012 г.) [28 мая 2011 г.]. «Основы кода Грея» . Практические советы по дизайну . ЭТаймс . Часть 1. Архивировано из оригинала 30 октября 2017 г. Проверено 30 октября 2017 г. Часть 2 Часть 3
Уоррен-младший, Генри С. (2013). «Глава 13: Код Грея». Хакерское наслаждение (2-е изд.). Аддисон Уэсли – Pearson Education, Inc., стр. 311–317. ISBN 978-0-321-84268-8 . (7 страниц)
Зиновик Игорь; Кренинг, Дэниел; Чебиряк, Юрий (21 марта 2008 г.). «Вычисление двоичных комбинаторных кодов Грея посредством исчерпывающего поиска с помощью решателей SAT» . Транзакции IEEE по теории информации . 54 (4). IEEE : 1819–1823 гг. дои : 10.1109/TIT.2008.917695 . hdl : 20.500.11850/11304 . S2CID 2854180 . (5 страниц)
О'Брайен, Джозеф А. (июнь 1957 г.). «Трансляторы двоично-десятичного кода с единичным расстоянием» . IRE-транзакции на электронных компьютерах . ИС-6 (2): 122–123. дои : 10.1109/TEC.1957.5221585 . ISSN 0367-9950 . Проверено 25 мая 2020 г. (2 страницы)
Барр, КГ (март 1981 г.). «Десятичный код Грея — легко преобразуется для кодирования положения вала» (PDF) . Беспроводной мир . Том. 87, нет. 1542. Факультет естественных наук Вест-Индского университета . стр. 86–87. Архивировано (PDF) из оригинала 28 июля 2020 г. Проверено 28 июля 2020 г.

Внешние ссылки

Демонстрация «Кода серого» Михаэля Шрайбера, Демонстрационный проект Wolfram (с реализацией Mathematica). 2007.
Словарь алгоритмов и структур данных NIST: код Грея .
Путеводитель по эволюционным вычислениям для путешествующих автостопом, вопрос 21: Что такое коды Грея и почему они используются? , включая код C для преобразования между двоичными файлами и BRGC.
Драгош А. Харабор использует коды Грея в 3D-дигитайзере .
Однодорожечные коды Грея, двоичные цепные коды ( Ланкастер, 1994 ) и регистры сдвига с линейной обратной связью — все они полезны для определения абсолютного положения с помощью однодорожечного поворотного энкодера (или другого датчика положения).
Столбец AMS: коды Грея
Колесный генератор оптического энкодера
ProtoTalk.net – Понимание квадратурного кодирования – более подробно описывает квадратурное кодирование с акцентом на роботизированные приложения.

[NB_Arithmetic_conversion-54] Jump up to: ^а ^б ^с Применяя простое правило инверсии , код Грея и код О'Брайена I можно перевести в чистый двоичный код 8421 и код Эйкена 2421 соответственно, чтобы облегчить арифметические операции. ^[С]

[NB_OEIS_A007814-61] Последовательность 0, 1, 0, 2, 0, 1, 0, 3,… (последовательность A007814 в OEIS ).

[NB_Modified-99] Jump up to: ^а ^б ^с Существует несколько вариантов кода Грея, которые называются «модифицированными»: код Гликсона иногда называют модифицированным кодом Грея. ^[Д] Код Лукала также называют модифицированным отраженным двоичным кодом (MRB). ^[И] Код О'Брайена I или код Уоттса иногда называют отраженным двоичным модифицированным кодом Грея. ^[Ф]

[NB_Petherick_OBrien-II-111] Jump up to: ^а ^б ^с ^д Поменяв местами и инвертировав три битовые строки, код О'Брайена II и код Петерика можно преобразовать друг в друга.

[NB_OBrien-I_Glixon-116] Jump up to: ^а ^б ^с ^д Поменяв местами две пары битовых рядов, индивидуально сдвинув четыре битовых ряда и инвертировав одну из них, код Гликсона и код О'Брайена I друг в друга. можно перевести

[NB_Other_codes-130] Другие BCD-коды единичного расстояния включают 5-битный код Либо-Крейга, не связанный с кодом Грея , и код 1-2-1 .

[NB_Weights-131] В зависимости от целевого применения кода, веса Хэмминга кода могут быть важными свойствами, выходящими за рамки теоретико-кодовых соображений, а также по физическим причинам. В некоторых обстоятельствах состояния полного сброса и/или состояния полной установки должны быть опущены (fe, чтобы избежать условий непроводимости или короткого замыкания), может оказаться желательным, чтобы максимальный используемый вес был как можно меньшим (fe, чтобы уменьшить мощность потребление схемы считывателя) или для того, чтобы разница используемых весов была небольшой (например, для уменьшения акустического шума или колебаний тока).

[NB_Tracks_Inverse-132] Jump up to: ^а ^б ^с Для Грея BCD , Пола и кодов Клара количество необходимых дорожек чтения может быть уменьшено с 4 до 3, если допустима инверсия одной из средних дорожек.

[NB_Complement_InvertTop-134] Jump up to: ^а ^б ^с ^д ^и ^ж Для кодов О'Брайена I и II и Петерика , Сасскинда , Клара а также кодов Эксцесса-3 Грея , дополнение до 9 может быть получено путем инвертирования наиболее значимой (четвертой) двоичной цифры.

[NB_Complement_Tompkins-137] Для кода Томпкинса II можно дополнение до девяти получить, инвертировав первые три цифры и поменяв местами две средние двоичные цифры.

[Lucal_1959-1] Jump up to: ^а ^б ^с Лукал, Гарольд М. (декабрь 1959 г.). «Арифметические операции для цифровых компьютеров с использованием модифицированного отраженного двоичного файла» . IRE-транзакции на электронных компьютерах . ЕС-8 (4): 449–458. дои : 10.1109/TEC.1959.5222057 . ISSN 0367-9950 . S2CID 206673385 . (10 страниц)

[Sellers-Hsiao-Bearnson_1968-2] Jump up to: ^а ^б ^с Селлерс-младший, Фредерик Ф.; Сяо, Му-Юэ; Бернсон, Лерой В. (ноябрь 1968 г.). Логика обнаружения ошибок для цифровых компьютеров (1-е изд.). Нью-Йорк, США: Книжная компания McGraw-Hill . стр. 152–164. LCCN 68-16491 . OCLC 439460 .

[3] Грей, Джоэл (март 2020 г.). «Понимание кода Грея: надежная система кодирования» . Graycode.ie . Раздел: Заключение . Проверено 30 июня 2023 г.

[Tompkins_1956-4] Jump up to: ^а ^б ^с ^д Томпкинс, Ховард Э. (сентябрь 1956 г.) [16 июля 1956]. «Двоично-десятичные коды единичного расстояния для двухпутевой коммутации» . IRE-транзакции на электронных компьютерах . Переписка. ИС-5 (3). Школа электротехники Мура , Пенсильванский университет , Филадельфия, Пенсильвания, США: 139. doi : 10.1109/TEC.1956.5219934 . ISSN 0367-9950 . Архивировано из оригинала 18 мая 2020 г. Проверено 18 мая 2020 г. (1 страница)

[Kautz_1958-5] Jump up to: ^а ^б Каутц, Уильям Х. (июнь 1958 г.). «Коды проверки ошибок на единичном расстоянии». IRE-транзакции на электронных компьютерах . ИС-7 (2): 179–180. дои : 10.1109/TEC.1958.5222529 . ISSN 0367-9950 . S2CID 26649532 . (2 страницы)

[Susskind_1958-6] Jump up to: ^а ^б Зюскинд, Альфред Крисс; Уорд, Джон Эрвин (28 марта 1958 г.) [1957, 1956]. «III.F. Коды единичного расстояния / VI.E.2. Отраженные двоичные коды». Написано в Кембридже, Массачусетс, США. В Зюскинде, Альфред Крисс (ред.). Замечания по методам аналого-цифрового преобразования . Книги по технологиям в области науки и техники. Том. 1 (3-е изд.). Нью-Йорк, США: Technology Press Массачусетского технологического института / John Wiley & Sons, Inc. / Chapman & Hall, Ltd., стр. 3-10–3-16 [3-13–3-16], 6-65. –6-60 [6-60]. (x+416+2 страницы) (Примечание. Содержание книги было первоначально подготовлено сотрудниками Лаборатории сервомеханизмов факультета электротехники Массачусетского технологического института для специальных летних программ, проводившихся в 1956 и 1957 годах. «Код чтения» Сасскинда " на самом деле является второстепенным вариантом показанного здесь кода, в котором две старшие битовые строки поменяны местами, чтобы лучше иллюстрировать симметрию. Кроме того, путем замены двух битовых строк местами и инвертировав одну из них, код можно перевести в код Петерика , тогда как, поменяв местами и инвертировав две битовые строки, код можно перевести в код Петерика. Код О'Брайена II .)

[Chinal_1973-7] Jump up to: ^а ^б Чинал, Жан П. (январь 1973 г.). «3.3. Коды расстояний единиц». Написано в Париже, Франция. Методы проектирования цифровых систем . Перевод Престона, Алан; Саммер, Артур (1-е изд. на английском языке). Берлин, Германия: Akademie-Verlag / Springer-Verlag . п. 50. дои : 10.1007/978-3-642-86187-1 . ISBN 978-0-387-05871-9 . S2CID 60362404 . Лицензия № 202-100/542/73. Артикул №7617470(6047) ES 19 B 1/20 K 3 . Проверено 21 июня 2020 г. (xviii+506 страниц) (Примечание. Оригинальная книга на французском языке 1967 года называлась «Техника логических значений и арифметических калькуляторов», опубликованная издательством Éditions Dunod [ fr ] .)

[MIL_1991-8] Jump up to: ^а ^б ^с ^д ^и ^ж Военный справочник: энкодеры — угол вала в цифровом формате (PDF) . Министерство обороны США . 1991-09-30. МИЛ-ХДБК-231А. Архивировано (PDF) из оригинала 25 июля 2020 г. Проверено 25 июля 2020 г. (Примечание. Заменяет MIL-HDBK-231(AS) (01.07.1970).)

[Spaulding_1954-9] Jump up to: ^а ^б ^с Сполдинг, Карл П. (12 января 1965 г.) [09 марта 1954 г.]. «Система цифрового кодирования и перевода» (PDF) . Монровия, Калифорния, США: Datex Corporation. Патент США 3165731А . Серийный номер 415058. Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 21 января 2018 г. (28 страниц)

[Russell_1964-10] Jump up to: ^а ^б Рассел, А. (август 1964 г.). «Некоторые двоичные коды и новый пятиканальный код» . Управление (системы, контрольно-измерительные приборы, обработка данных, автоматизация, управление, включая прогресс автоматизации) . Специальные возможности. 8 (74). Лондон, Великобритания: Morgan-Grampain (Publishers) Limited: 399–404 . Проверено 22 июня 2020 г. (6 страниц)

[Stibitz_1941-11] Jump up to: ^а ^б ^с Стибиц, Джордж Роберт (12 января 1943 г.) [26 ноября 1941 г.]. «Двоичный счетчик» . Нью-Йорк, США: Bell Telephone Laboratories, Incorporated . Патент США 2307868 . Серийный № 420537 . Проверено 24 мая 2020 г. п. 2, правый столбец, строки 43–73: […] Более четкое представление о положении шаров после каждого импульса будет получено, если набор шаров будет представлен числом, имеющим одинаковое количество цифр, каждая из которых может иметь одно из двух произвольных значений, например 0 и 1. Если верхняя позиция называется 0, а нижняя позиция […] 1, то настройку счетчика […] можно прочитать слева направо как 0 100 000. […] Ниже приводится перевод количества полученных импульсов в эту форму двоичной записи для первых шестнадцати импульсов, полученных на первых пяти шарах […] Число импульсов […] Двоичная запись […] [1] (4 страницы )

[Winder_1959-12] Jump up to: ^а ^б ^с ^д ^и Уиндер, К. Фаррелл (октябрь 1959 г.). «Энкодеры угла вала обеспечивают высокую точность» (PDF) . Электронная промышленность . 18 (10). Компания Чилтон : 76–80. Архивировано из оригинала (PDF) 28 сентября 2020 г. Проверено 14 января 2018 г. п. 78: […] Тип кодового колеса, наиболее популярный в оптических кодировщиках, содержит шаблон циклического двоичного кода, предназначенный для создания циклической последовательности выходных сигналов «вкл-выкл». Циклический двоичный код также известен как код циклической прогрессии, отраженный двоичный код и код Грея. Этот код был разработан Г. Р. Стибитцем из Bell Telephone Laboratories и впервые был предложен для импульсно-кодовой модуляции систем Фрэнком Греем , также из BTL. Отсюда и название кода Грея. Код Грея или циклический код используется главным образом для исключения возможности ошибок при переходе кода, которые могут привести к серьезной неоднозначности. […]

[Knuth_2014-13] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Кнут, Дональд Эрвин (12 сентября 2014 г.). «Перечисление и возврат/Генерация всех n -кортежей» . Искусство компьютерного программирования, Том 4А: Комбинаторные алгоритмы, Часть 1 . Том. 4А (1-е изд.). Аддисон-Уэсли Профессионал . стр. 442–443. ISBN 978-0-13348885-2 . (912 страниц)

[Gray_1947-14] Jump up to: ^а ^б Грей, Фрэнк (17 марта 1953 г.) [13 ноября 1947 г.]. Импульсно-кодовая связь (PDF) . Нью-Йорк, США: Bell Telephone Laboratories, Incorporated . Патент США 2632058 . Серийный номер 785697. Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 5 августа 2020 г. (13 страниц)

[Goldberg_1989-15] Jump up to: ^а ^б Голдберг, Дэвид Эдвард (1989). Генетические алгоритмы в поиске, оптимизации и машинном обучении (1-е изд.). Ридинг, Массачусетс, США: Аддисон-Уэсли . Бибкод : 1989gaso.book.....G .

[Breckman_1953-16] Брекман, Джек (31 января 1956 г.) [31 декабря 1953 г.]. Схема кодирования (PDF) . Лонг-Бранч, Нью-Джерси, США: Министр армии США . Патент США 2733432 . Серийный номер 401738. Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 5 августа 2020 г. (8 страниц)

[Ragland-Schultheis_1953-17] Jump up to: ^а ^б Рэгланд, граф Альберт; Шультайс-младший, Гарри Б. (11 февраля 1958 г.) [16 октября 1953 г.]. Чувствительная к направлению система управления положением с двоичным кодом (PDF) . Северный Голливуд, Калифорния, США: Bendix Aviation Corporation. Патент США 2823345 . Серийный номер 386524. Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 5 августа 2020 г. (10 страниц)

[Domeshek-Reiner_1954-18] Домашек, Сол; Райнер, Стюарт (24 июня 1958 г.) [8 января 1954 г.]. Автоматическая система выпрямления (PDF) . Министр военно-морского флота США . Патент США 2839974 . Серийный номер 403085. Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 5 августа 2020 г. (8 страниц)

[Petherick_1953-19] Jump up to: ^а ^б ^с Петерик, Эдвард Джон (октябрь 1953 г.). Циклическая прогрессивная двоично-десятичная система представления чисел (Техническое примечание MS15). Фарнборо, Великобритания: Королевское авиастроительное предприятие (RAE). (4 страницы) (Примечание. Иногда ее называют циклической двоично-десятичной системой представления чисел .)

[Evans_1960-20] Jump up to: ^а ^б Эванс, Дэвид Сильвестр (1960). Основы цифрового приборостроения (1-е изд.). Лондон, Великобритания: Hilger & Watts Ltd. Проверено 24 мая 2020 г. (39 страниц)

[Evans_1961-21] Jump up to: ^а ^б Эванс, Дэвид Сильвестр (март 1961 г.). «Глава третья: Прямое считывание с закодированных весов». Цифровые данные: их получение и обработка для анализа и управления процессами (1-е изд.). Лондон, Великобритания: Hilger & Watts Ltd / Interscience Publishers . стр. 18–23 . Проверено 24 мая 2020 г. п. 20–23: […] Расшифровка. […] Для декодирования кодов CPB или WRD можно применить простое правило инверсии. Показания верхних дорожек определяют способ трансляции нижних дорожек. Правило инверсии применяется построчно для CPB, а для WRD — десятилетие за десятилетием или построчно. Поэтому, начиная с верхнего или самого медленно меняющегося трека CPB, если результат нечетный (1), значение следующего трека должно быть инвертировано, т.е. 0 для 1 и 1 для 0. Однако, если первый трек четный (0 ), вторая дорожка остается прочитанной, т.е. 0 вместо 0 и 1 вместо 1. Опять же, если результирующее чтение второй дорожки нечетное, чтение третьей дорожки инвертируется и так далее. Когда нечетное число меняется на четное, строка ниже не инвертируется, а когда четное число меняется на нечетное, строка ниже инвертируется. Результатом применения этого правила к шаблону […] является чисто двоичный шаблон (PB) […], где каждой дорожке или цифре может быть присвоено определенное числовое значение (в данном случае 1, 2, 4, 8 и т. д.). […] Использование правила построчной инверсии в коде WRD создает шаблон [a] [ кода 1, 2, 4, 2 ], в котором цифрам снова могут быть присвоены числовые значения и суммированы десятилетие за десятилетием. Суммирование цифр может быть очень полезным, например, в системе высокоскоростного сканирования; но в системе параллельного декодирования […] обычно каждый двоичный квартет или декаду рассматривают как единое целое. Другими словами, если первая или более значимая декада нечетная, вторая декада исправляется или дополняется путем инвертирования дорожки D и т. д. Результатом является повторяющийся шаблон [исправленного кода WRD]. Этого чрезвычайно легко достичь, поскольку единственное требуемое изменение — это инверсия значения дорожки D или дополняющей цифры. […] (8+82 страницы) (Примечание. Автор вообще не упоминает Грея и называет стандартный код Грея «Циклическим перестановочным двоичным кодом» (CPB), в указателе книги он ошибочно указан как «циклический чистый двоичный код». )

[Newson_1965-22] Ньюсон, Пенсильвания (1965). Таблицы двоичного кодирования углов (1-е изд.). Управление по атомной энергии Соединенного Королевства , Исследовательская группа, Научно-исследовательский институт атомной энергии , Харвелл, Великобритания: Канцелярский офис Ее Величества . Проверено 24 мая 2020 г. (12 страниц)

[Heath_1961-23] Хит, ФГ (сентябрь 1961 г.). «Пионеры двоичного кодирования» . Журнал Института инженеров-электриков . 7 (81). Манчестерский колледж науки и технологий , технологический факультет Манчестерского университета , Манчестер, Великобритания: Институт инженерии и технологий (IET): 539–541. дои : 10.1049/jiee-3.1961.0300 . Архивировано из оригинала 28 марта 2020 г. Проверено 22 июня 2020 г. (3 страницы)

[Cattermole_1969-24] Каттермоул, Кеннет В. (1969). Написано в Харлоу, Эссекс, Великобритания. Принципы импульсно-кодовой модуляции (1-е изд.). Лондон, Великобритания / Нью-Йорк, США: Iliffe Books Ltd. / American Elsevier Publishing Company, Inc., стр. 245, 434. ISBN. 978-0-444-19747-4 . LCCN 78-80432 . СБН 444-19747-8 . п. 245: […] Кажется, существует некоторая путаница в атрибуции этого кода, поскольку с ним были связаны два изобретателя по имени Грей. Когда я впервые услышал это имя, я решил, что оно относится к Элише Грею , и Хит свидетельствует, что он использовал его. Многие считают, что это относится к Фрэнку Грею из Bell Telephone Laboratories , который в 1947 году впервые предложил использовать его в кодирующих трубках : его патент указан в библиографии. […] (2+448+2 страницы)

[Edwards_2004-25] Эдвардс, Энтони Уильям Фэрбанк (2004). Зубчатые колеса разума: история диаграмм Венна . Балтимор, Мэриленд, США: Издательство Университета Джонса Хопкинса . стр. 48, 50. ISBN. 0-8018-7434-3 .

[Gros_1872-26] Гро, Люк-Агатон-Луи (1872). Théorie du Baguenodier par un clerc de notaire lyonnais (на французском языке) (1-е изд.). Лион, Франция: Эме Вентринье . Архивировано из оригинала 3 апреля 2017 г. Проверено 17 декабря 2020 г. [2] (2+16+4 страницы и 4 страницы в развороте) (Примечание. Этот буклет был опубликован анонимно, но известно, что его автором является Луи Гро.)

[Lucas_1883-27] Лукас, Эдуард (ноябрь 1883 г.). Ханойская башня: настоящая аннамская головоломка — игра, привезенная из Тонкина профессором Н. Клаусом (из Сиама) мандарином из колледжа Ли Су Стиан! (на французском языке). Типография Поля Бусреза, Тур. (Примечание: Клаус де Сиам — анаграмма Лукаса д'Амьена, псевдонима автора Эдуарда Лукаса .)

[Parville_1883-28] де Парвиль, Анри [на французском языке] , изд. (27 декабря 1883 г.). "Ханойская башня, настоящая аннамская головоломка, игра, привезенная из Тонкина профессором Н. Клаусом (из Сиама), мандарином колледжа Ли-Су-Стиан. Действительно, головоломка, но интересная. Мы" Мы не можем лучше благодарить мандарина за его доброе намерение по отношению к мирянину, чем указывать на Ханойскую башню терпеливым людям, одержимым демоном азартных игр » . Журнал политических и литературных дебатов (обзор). Revue des Sciences (на французском языке) (изд. Matin). Париж, Франция: 1–2 [2]. ковчег:/12148/bpt6k462461g. Архивировано из оригинала 18 декабря 2020 г. Проверено 18 декабря 2020 г. (1 страница)

[Allardice-Fraser_1883-29] Аллардис, RE; Фрейзер, А.Ю. (февраль 1883 г.). Аллардис, Роберт Эдгар ; Фрейзер, Александр Юл (ред.). «Тур в Ханое» . Труды Эдинбургского математического общества (на английском и французском языках). 2 (5). Эдинбургское математическое общество : 50–53. дои : 10.1017/S0013091500037147 . eISSN 1464-3839 . ISSN 0013-0915 . S2CID 122159381 . [3] (4 страницы)

[Lucas_1892-30] Лукас, Эдуард (1979) [1892]. Математические развлечения (на французском языке). Том. 3 (переиздание Библиотеки Альберта Бланшара). стр. 58. (Первое издание этой книги вышло посмертно.)

[Herter-Rote_2016-31] Jump up to: ^а ^б Гертер, Феликс; Роте, Гюнтер (14 ноября 2018 г.) [09 августа 2018 г., 12 августа 2017 г., 09 августа 2017 г., 22 апреля 2016 г.]. «Бесконтурное перечисление кода Грея и Бухарестская башня» (PDF) . Теоретическая информатика . 748 . Берлин, Германия: 40–54. arXiv : 1604.06707 . дои : 10.1016/j.tcs.2017.11.017 . ISSN 0304-3975 . S2CID 4014870 . Архивировано (PDF) из оригинала 16 декабря 2020 г. Проверено 16 декабря 2020 г. [4] (15/18/19/24 страниц)

[Gardner_1972-32] Гарднер, Мартин (август 1972 г.). «Любопытные свойства кода Грея и как его можно использовать для решения головоломок». Научный американец . Математические игры . Том. 227, нет. 2. п. 106. (1 страница)

[Zeman-Fischer_1877-33] Земан, Джон; Фишер, Фердинанд, ред. (1877). «Некоторые недавние предложения по множественной телеграфии: А. Попунктная множественная телеграфия» . Политехнический журнал Динглера (на немецком языке). 226 . Аугсбург, Германия: JG Cotta'sche Buchhandlung : 499–507. Архивировано из оригинала 21 декабря 2020 г. Проверено 21 декабря 2020 г. п. ] [ ... ]

[Froehlich-Kent_1991-34] Бутрика, Эндрю Дж. (21 июня 1991 г.). «Бодо, Жан Морис Эмиль» . В Фрелихе, Фриц Э.; Кент, Аллен ; Холл, Кэролайн М. (ред.). Энциклопедия телекоммуникаций Фрелиха/Кента: Том 2 - От батарей к кодам - Телекоммуникации . Том. 2. Марсель Деккер Инк. / CRC Press . стр. 31–34. ISBN 0-8247-2901-3 . LCCN 90-3966 . Проверено 20 декабря 2020 г. п. 31: […] Прототип Бодо (4 года создания) был построен в 1876 году. Передатчик имел 5 клавиш, похожих на клавиши фортепиано. Сообщения передавались в специальном 5-элементном коде, разработанном Бодо […]

[Fischer_2000-35] Фишер, Эрик Н. (20 июня 2000 г.). «Эволюция кодов символов, 1874–1968» . ковчег:/13960/t07x23w8s . Проверено 20 декабря 2020 г. […] В 1872 году [Бодо] начал исследования телеграфной системы, которая позволила бы нескольким операторам одновременно передавать данные по одному проводу и по мере получения передач печатать их обычными буквенными символами на полоске бумаги. Он получил патент на такую систему 17 июня 1874 года. […] Вместо переменной задержки, за которой следует одиночный импульс, система Бодо использовала одинаковые шесть единиц времени для передачи каждого символа. […] его ранний телеграф, вероятно, использовал шестизначный код […], который он приписывает Дэви в статье 1877 года. […] в 1876 году Бодо перепроектировал свое оборудование, чтобы использовать пятизначный код. Однако иногда знаки препинания и цифры по-прежнему были необходимы, поэтому он перенял у Хьюза использование двух специальных символов буквенного и цифрового пространства, которые заставляли принтер переключаться между регистрами одновременно с продвижением бумаги без печати. Пятизначный код, который он начал использовать в это время […], был структурирован так, чтобы соответствовать его клавиатуре […], которая управляла двумя единицами каждого символа с помощью переключателей, управляемых левой рукой, а остальные три единицы — правой рукой. […] [5] [6]

[Rothen_1884-36] Ротен, Тимофей (25 декабря 1884 г.). «Телеграфный принтер Бодо» . Журнал Télégraphique (на французском языке). VIII/№16 (12). Берн, Швейцария: Международное бюро телеграфной администрации: 241–253 [249]. eISSN 2725-738X . ISSN 2223-1420 . ковчег:/12148/bpt6k5725454q. Архивировано из оригинала 21 декабря 2020 г. Проверено 20 декабря 2020 г.

[Pendry_1920-37] Пендри, Генри Уолтер (1920) [октябрь 1919]. Написано в Лондоне, Великобритания. Телеграфная система печати Бодо (2-е изд.). Лондон, Бат, Мельбурн, Нью-Йорк: Сэр Исаак Питман и сыновья, Ltd., стр. 43–44. LCCN 21005277 . OCLC 778309351 . ОЛ 6633244М . Проверено 20 декабря 2020 г. (vii+184 страницы) (Примечание. Первое издание вышло в 1913 году.)

[MacMillan_2010-38] Jump up to: ^а ^б Макмиллан, Дэвид М. (27 апреля 2010 г.) [25 апреля 2010 г., 23 апреля 2010 г.]. «Коды, которые не считаются - некоторые печатные телеграфные коды как продукты своих технологий (с особым вниманием к теленаборному устройству)» . Лемур.com . Редакция 3. Минерал-Пойнт, Висконсин, США. Архивировано из оригинала 18 декабря 2020 г. Проверено 20 декабря 2020 г.

[ITU_1909-39] Написано в Лиссабоне, Португалия. Международная телеграфная конвенция Санкт-Петербурга и прилагаемые к ней правила и тарифы, Лиссабонская пересмотренная версия, 1908 г. / Выдержки из издания: Документы Лиссабонской международной телеграфной конференции (на французском языке). Берн, Швейцария: Международное бюро Телеграфного союза . 1909 [1908].

[ITU_1933_FR-40] «Глава IX. Сигналы передачи, Статья 35. Сигналы передачи международных телеграфных алфавитов №№ 1 и 2, сигналов азбуки Морзе, аппарата Хьюза и аппарата Сименса». Написано в Мадриде, Испания. Правила телеграфной связи, прилагаемые к международной конвенции электросвязи - заключительный протокол к указанному постановлению - Мадрид, 1932 г. (PDF) (на французском языке). Берн, Швейцария: Международное бюро Телеграфного союза . 1933 [1932]. стр. 31–40 [33]. Архивировано (PDF) из оригинала 21 декабря 2020 г. Проверено 21 декабря 2020 г. (1+188 страниц) [7]

[ITU_1933_EN-41] «Глава IX. Сигналы передачи. Статья 35. Сигналы передачи международных телеграфных алфавитов №№ 1 и 2, сигналов азбуки Морзе и сигналов приборов Хьюза и Сименса.». Регламент телеграфии, прилагаемый к Международной конвенции электросвязи - Заключительный протокол к Регламенту телеграфии - Мадрид, 1932 г. (PDF) (на английском и французском языках). Лондон, Великобритания: Главное почтовое отделение / Канцелярия Его Величества . 1933 [1932]. С. 32–40 [34]. 43-152-2 / 18693. Архивировано (PDF) из оригинала 21 декабря 2020 г. Проверено 21 декабря 2020 г. (1+2*120+26 страниц) [8]

[Zemanek_1979-42] Земанек, Генрих «Хайнц» Йозеф (1 декабря 1983 г.). Отто Шеффлер (1838–1928). Пионер телефона, телеграфии и перфокарт, а также строитель первой телефонной станции в Вене . Листы по истории техники (на немецком и английском языках). Том 41–43 (1979–1981) (1-е изд.). Вена, Австрия: Технический музей промышленности и торговли , Научно-исследовательский институт истории техники / Springer-Verlag . стр. 81–118. ISBN 3-21181779-4 . ISSN 0067-9127 . OCLC 952698275 .

[Zemanek_1976-43] Земанек, Генрих «Хайнц» Йозеф (7 июня 1976 г.). «Компьютерная предыстория и история в Центральной Европе» . Написано в Вене, Австрия. Международный семинар по управлению знаниями в области требований . AFIPS '76: Материалы национальной компьютерной конференции и выставки 7–10 июня 1976 г., июнь 1976 г. Vol. 1. Нью-Йорк, США: Американская федерация обществ обработки информации , Ассоциация вычислительной техники . стр. 15–20. дои : 10.1145/1499799.1499803 . ISBN 978-1-4503-7917-5 . S2CID 14114959 . Архивировано из оригинала 17 декабря 2020 г. Проверено 17 декабря 2020 г. п. 17: […] В 1874 году Шеффлер [ де ] изобрел еще один печатный телеграф , четверную систему, подобную Бодо , но механически более сложную. Телеграф Хьюза имел два синхронно вращающихся пальца: один в отправителе, другой в приемнике. С помощью клавиатуры, напоминающей фортепиано, оператор выбирал букву и тем самым прикасался к вращающемуся пальцу в соответствующем направлении. Поскольку принимающий палец в этот момент находился в том же направлении, получатель мог напечатать правильную букву. Печатные телеграфы Бодо и Шеффлера используют пятибитный двоичный код. ... Код Шеффлера — это отраженный двоичный код! То, что Ф. Грей запатентовал в 1953 году для PCM , Шеффлер применил в своем телеграфе в 1874 году по той же причине: надежность. Контактными пальцами он считывал на пяти камерах последовательно все комбинации; правый запускает печать. Если пальцы должны совершать минимальное количество движений, решением является отраженный двоичный код. Для Schaeffler эта идея была второстепенной. Точнее, код описан в письме сотрудника австрийской почты Йохана Н[эпомука] Тойфельхарта, вставлено туда в виде сноски и сообщает, что Шеффлер нашел код, комбинируя деревянные бруски с различными комбинациями, пока не нашел лучшее решение. Другой сотрудник Почты, Александр Вильгельм Ламберт из Линца, утверждает, что показал этот код Шеффлеру еще в 1872 году, но это утверждение неясно и не может быть проверено. […] (6 страниц)

[Goodall_1951-44] Гудолл, Уильям М. (январь 1951 г.). «Телевидение с импульсно-кодовой модуляцией». Технический журнал Bell System . 30 (1): 33–49. дои : 10.1002/j.1538-7305.1951.tb01365.x . (Примечание. Представлено устно на Национальном съезде IRE, Нью-Йорк, март 1949 г.)

[Karnaugh_1953-45] Карно, Морис (ноябрь 1953 г.) [23 апреля 1953 г., 17 марта 1953 г.]. «Метод карт для синтеза комбинационных логических схем» (PDF) . Труды Американского института инженеров-электриков, Часть I: Связь и электроника . 72 (5): 593–599. дои : 10.1109/TCE.1953.6371932 . S2CID 51636736 . Документ 53-217. Архивировано из оригинала (PDF) 16 апреля 2017 г. Проверено 16 апреля 2017 г. (Примечание. Также содержится краткий обзор Сэмюэля Х. Колдуэлла .)

[Wakerly_1994-46] Уэйкерли, Джон Ф. (1994). Цифровой дизайн: принципы и практика . Нью-Джерси, США: Прентис Холл . стр. 48–49, 222. ISBN. 0-13-211459-3 . (Примечание. В двух разделах страницы, взятых вместе, говорится, что K-карты помечены кодом Грея. В первом разделе говорится, что они помечены кодом, который изменяется только на один бит между записями, а во втором разделе говорится, что такой код называется Греем. код.)

[Brown_2012-47] Браун, Фрэнк Маркхэм (2012) [2003, 1990]. «3.9.2 Карты». Булево рассуждение - Логика булевых уравнений (переиздание 2-го изд.). Минеола, Нью-Йорк, США: Dover Publications, Inc., с. 49. ИСБН 978-0-486-42785-0 . п. 49: […] Карта Карно упорядочивает аргументы дискриминантов в соответствии с отраженным двоичным кодом, также называемым кодом Грея. […] (xii+291+3 страницы) 1-е издание

[Händler_1958-48] Дилер, Вольфганг (1958). Метод минимизации синтеза схем (графов минимизации) (диссертация) (на немецком языке). Потсдам, Германия: Дармштадтский технологический университет . Д 17. (73 стр.+прил.) [9]

[Steinbuch-Wagner_1967-49] Бергер, Эрих Р.; Купец, Вольфганг (1967) [1962]. Штайнбух, Карл В .; Вагнер, Зигфрид В. (ред.). Обработка сообщений в мягкой обложке (на немецком языке) (2-е изд.). Берлин, Германия: Springer-Verlag OHG . стр. 64, 1034–1035, 1036, 1038. LCCN 67-21079 . Название №. 1036. с. 64: […] Представление по дилеру является ясным , в котором все точки, пронумерованные в соответствии с кодом Грея […], располагаются в окрестностях круга. Однако для этого требуется много места. […] [ Диаграмма дилера , где все точки, пронумерованные по коду Грея , расположены на окружности, легко понятна. Однако для этого требуется много места.]

[ISER_1-50] «Коллекция информатики Эрланген (ISER)» (на немецком языке). Эрланген, Германия: Университет Фридриха-Александра . 13 марта 2012 г. Архивировано из оригинала 16 мая 2017 г. Проверено 12 апреля 2017 г.

[ISER_2-51] «Коллекция компьютерных наук Эрланген (ISER) – выходные данные» (на немецком языке). Эрланген, Германия: Университет Фридриха-Александра . 13 марта 2012 г. Архивировано из оригинала 26 февраля 2012 г. Проверено 15 апреля 2017 г.

[Bhat-Savage_1996-52] Jump up to: ^а ^б ^с ^д ^и Бхат, Гириш С.; Сэвидж, Карла Дайан (1996). «Сбалансированные коды Грея» . Электронный журнал комбинаторики . 3 (1). дои : 10.37236/1249 .

[Donohue_2003-53] Донохью, Райан (2003). «Синхронизация в цифровых логических схемах» (PDF) . Архивировано (PDF) из оригинала 15 января 2018 г. Проверено 15 января 2018 г.

[Hulst_1957-55] Хюлст, Джордж Д. (6 февраля 1962 г.) [15 ноября 1957 г.]. Отраженный счетчик двоичного кода (PDF) . Натли, Нью-Джерси, США: Международная телефонная и телеграфная корпорация (ITT). Патент США 3020481 . Серийный номер 696793. Архивировано (PDF) из оригинала 6 августа 2020 г. Проверено 6 августа 2020 г. (5 страниц)

[Powell_1968-56] Jump up to: ^а ^б ^с ^д Пауэлл, Э. Александр (июнь 1968 г.). «Коды, особенно полезные для аналого-цифрового преобразования». Краткое примечание о полезных кодах для схем управления жидкостью (PDF) . Крэнфилд, Великобритания: Колледж аэронавтики , факультет технологии производства. стр. 7, 9. S2CID 215864694 . Памятка CoA 156. Архивировано (PDF) из оригинала 15 декабря 2020 г. Проверено 15 декабря 2020 г. (18 страниц) (Примечание. В статье код Гликсона называется модифицированным кодом Грея , а Ричарда В. Хэмминга написано с ошибкой.) имя

[Mehta-Owens-Irwin_1996-57] Мехта, Хузефа; Оуэнс, Роберт Майкл; Ирвин, Мэри Джейн «Джэни» (22 марта 1996 г.). «Некоторые проблемы с адресацией кода Грея» . Материалы шестого симпозиума Великих озер по СБИС . Компьютерное общество IEEE . стр. 178–181. дои : 10.1109/ГЛСВ.1996.497616 . ISBN 978-0-8186-7502-7 . ISSN 1066-1395 . S2CID 52837310 .

[Doran_2007-58] Jump up to: ^а ^б Доран, Роберт «Боб» Уильям (март 2007 г.). Код Грея (PDF) . Серия отчетов об исследованиях CDMTCS. Центр дискретной математики и теоретической информатики, Оклендский университет , Новая Зеландия. КДМТСС-304. Архивировано (PDF) из оригинала 22 мая 2020 г. Проверено 23 мая 2020 г. (25 страниц)

[Su-Tsui-Despain_1994-59] Су, Чинг-Лун; Цуй, Чи-Ин; Деспейн, Элвин М. (1994). Методы проектирования и компиляции архитектуры малой мощности для высокопроизводительных процессоров (PDF) (Отчет). Лаборатория передовой компьютерной архитектуры. АКАЛ-ТР-94-01. Архивировано (PDF) из оригинала 26 июля 2020 г. Проверено 17 декабря 2020 г.

[Guo-Parameswaran_2010-60] Го, Хуэй; Парамешваран, Шри (апрель – июнь 2010 г.). «Кодировка со сдвигом Грея для уменьшения переключения шины адреса памяти команд для встраиваемых систем с низким энергопотреблением». Журнал системной архитектуры . 56 (4–6): 180–190. дои : 10.1016/j.sysarc.2010.03.003 .

[Dietz_2002-62] Дитц, Генри Гордон «Хэнк» (2002). «Агрегатные магические алгоритмы: преобразование кода Грея» . Агрегат . Кафедра электротехники и вычислительной техники Инженерного колледжа Университета Кентукки . Архивировано из оригинала 16 декабря 2020 г. Проверено 16 декабря 2020 г.

[63] Максфилд, Макс (29 июня 2007 г.). «Как генерировать коды Грея для последовательностей, не равных степени двойки» . Архивировано из оригинала 29 января 2022 г. Проверено 29 января 2022 г.

[64] (последовательность A290772 в OEIS )

[Guan_1998-65] Jump up to: ^а ^б Гуан, Дах-Джых (1998). «Обобщенные коды Грея с приложениями». Труды Национального научного совета Китайской Республики, Часть А. 22 : 841–848. CiteSeerX 10.1.1.119.1344 .

[66] Д. Г. Вагнер, Дж. Уэст (1991). «Построение унифицированных кодов Грея». Конгресс Нумерантиум . 80 : 217–223.

[Suparta_2005-67] Jump up to: ^а ^б Супарта, И. Ненгах (2005). «Простое доказательство существования экспоненциально сбалансированных кодов Грея» . Электронный журнал комбинаторики . 12 . дои : 10.37236/1986 .

[Flahive-Bose_2007-68] Jump up to: ^а ^б Флахайв, Мэри Элизабет ; Бозе, Белла (2007). «Балансировка циклических R -арных кодов Грея» . Электронный журнал комбинаторики . 14 . дои : 10.37236/949 .

[Strackx-Piessens_2016-69] Стракс, Рауль; Писсенс, Франк (2016). «Ариадна: минимальный подход к непрерывности государства» . Усеникс Безопасность . 25 .

[70] Сэвидж, Карла Дайан (1997). «Обзор комбинаторных кодов Грея» . Обзор СИАМ . 39 (4). Общество промышленной и прикладной математики (SIAM): 605–629. Бибкод : 1997SIAMR..39..605S . CiteSeerX 10.1.1.39.1924 . дои : 10.1137/S0036144595295272 . JSTOR 2132693 . S2CID 6375360 .

[Savage-Winkler_1995-71] Jump up to: ^а ^б Сэвидж, Карла Дайан ; Винклер, Питер (1995). «Монотонные коды Грея и проблема средних уровней» . Журнал комбинаторной теории . Серия А. 70 (2): 230–248. дои : 10.1016/0097-3165(95)90091-8 . ISSN 0097-3165 .

[Savage_1997-72] Сэвидж, Карла Дайан (16 января 1997 г.). «Длинные циклы на средних двух уровнях булевой решетки» . Арс Комбинатория . 35 (А). Государственный университет Северной Каролины, Роли, Северная Каролина, США: 97–108. CiteSeerX 10.1.1.39.2249 . ISSN 0381-7032 . S2CID 15975960 . Архивировано из оригинала 13 мая 2020 г. Проверено 13 мая 2020 г. (15 страниц)

[Goddyn_1999-73] Jump up to: ^а ^б Годдин, Луис (1999). «MATH 343 Дополнительные материалы по прикладной дискретной математике» (PDF) . Департамент математики Университета Саймона Фрейзера . Архивировано из оригинала (PDF) 17 февраля 2015 г.

[Sawada-Wong_2007-74] Савада, Джозеф «Джо»; Вонг, Деннис Чи-Хим (2007). «Быстрый алгоритм генерации кодов Беккета – Грея». Электронные заметки по дискретной математике . 29 : 571–577. дои : 10.1016/j.endm.2007.07.091 .

[Richards_1971-75] Ричардс, Ричард Колер (январь 1971 г.). «Коды змеи в коробке». Написано в Эймсе, Айова, США. Цифровой дизайн . Нью-Йорк, США: Wiley-Interscience , John Wiley & Sons, Inc., стр. 206–207. ISBN 0-471-71945-5 . LCCN 73-147235 . (12+577+1 стр.)

[Spedding_1994_1-76] Jump up to: ^а ^б Новая Зеландия 264738 , Спеддинг, Норман Брюс, «Кодер положения», опубликовано 28 октября 1994 г. ^{[ не удалось пройти проверку ]}

[Spedding_1994_2-77] Спеддинг, Норман Брюс (28 октября 1994 г.). «Ниже представлена копия предварительного патента, поданного от имени Industrial Research Limited 28 октября 1994 г. – Патент Новой Зеландии 264738» (PDF) . Индустриальные Исследования Лимитед. Патент Новой Зеландии 264738. Архивировано (PDF) из оригинала 29 октября 2017 г. Проверено 14 января 2018 г.

[Hiltgen-Paterson-Brandestini_1996-78] Хильтген, Ален П.; Патерсон, Кеннет Г.; Брандестини, Марко (сентябрь 1996 г.). «Однодорожечные коды Грея» . Транзакции IEEE по теории информации . 42 (5): 1555–1561. дои : 10.1109/18.532900 . Збл 857.94007 .

[Hiltgen-Paterson_2001-79] Хильтген, Ален П.; Патерсон, Кеннет Г. (сентябрь 2001 г.). «Коды однопутных цепей» (PDF) . Транзакции IEEE по теории информации . 47 (6): 2587–2595. CiteSeerX 10.1.1.10.8218 . дои : 10.1109/18.945274 . Архивировано (PDF) из оригинала 15 января 2018 г. Проверено 15 января 2018 г.

[Etzion-Schwartz_1999-80] Эцион, Туви; Шварц, Моше (ноябрь 1999 г.) [17 мая 1998 г.]. «Структура однодорожечных кодов Грея» (PDF) . Транзакции IEEE по теории информации . ИТ-45 (7): 2383–2396. CiteSeerX 10.1.1.14.8333 . дои : 10.1109/18.796379 . Архивировано (PDF) из оригинала 15 января 2018 г. Проверено 15 января 2018 г. Технический отчет CS0937. Архивировано 15 декабря 2018 г. на Wayback Machine.

[Sillke_1997-81] Силке, Торстен (1997) [1993-03-01]. «Грей-коды с небольшим количеством треков (вопрос Марко Брандестини)» . Архивировано из оригинала 29 октября 2017 г. Проверено 29 октября 2017 г.

[Etzion-Paterson_1996-82] Jump up to: ^а ^б Эцион, Туви; Патерсон, Кеннет Г. (май 1996 г.). «Почти оптимальные однодорожечные коды Грея» (PDF) . Транзакции IEEE по теории информации . ИТ-42 (3): 779–789. CiteSeerX 10.1.1.14.1527 . дои : 10.1109/18.490544 . Архивировано (PDF) из оригинала 30 октября 2016 г. Проверено 8 апреля 2018 г.

[Ruskey_2005-83] Раски, Фрэнк ; Уэстон, Марк (18 июня 2005 г.). «Обзор диаграмм Венна: симметричные диаграммы» . Динамические опросы. Электронный журнал комбинаторики . дои : 10.37236/26 .

[Alciatore-Histand_1999-84] Альсиаторе, Дэвид Г.; Хистанд, Майкл Б. (1999). Мехатроника . Образование МакГроу – Хилла – Европа. ISBN 978-0-07-131444-2 .

[Experts_Exchange_Williams_2008-85] Уильямс, Гэри (25 июля 2008 г.). « Однодорожечный код Грея предназначен для кодирования на 360 градусов с помощью 9 датчиков» . Обмен экспертами .

[Thingiverse_9-Bit_Singletrack_Gray_Code_Rotorary_Encoder-86] Бауэр, Флориан. «9-битный абсолютный однодорожечный поворотный энкодер с кодом Грея» . Тингиверс .

[Krishna_2008-87] Кришна (11 мая 2008 г.). «Код Грея для QAM» . Архивировано из оригинала 29 октября 2017 г. Проверено 29 октября 2017 г.

[Strang-Dammann-Roeckl-Plass_2009-88] Стрэнг, Томас; Дамманн, Армин; Рёкль, Матиас; Пласс, Саймон (октябрь 2009 г.). Использование кодов Грея в качестве идентификаторов местоположения (PDF) . 6-я экспертная дискуссия GI/ITG КуВС Геолокационные приложения и сервисы (на английском и немецком языках). Оберпфаффенхофен, Германия: Институт связи и навигации, Немецкий аэрокосмический центр (DLR). CiteSeerX 10.1.1.398.9164 . Архивировано (PDF) из оригинала 1 мая 2015 г. Проверено 16 декабря 2020 г. (5/8 страниц) [10]
Томас Стрэнг; и др. (октябрь 2009 г.). «Использование кодов Грея в качестве идентификаторов местоположения» (PDF) . ResearchGate (Аннотация) (на немецком и английском языках). Архивировано из оригинала 03 сентября 2020 г.

[97] Томас Стрэнг; и др. (октябрь 2009 г.). «Использование кодов Грея в качестве идентификаторов местоположения» (PDF) . ResearchGate (Аннотация) (на немецком и английском языках). Архивировано из оригинала 03 сентября 2020 г.

[Greferath_2009-89] Греферат, Маркус (2009). «Введение в теорию кольцевого линейного кодирования». В комнате, Массимилиано; Мора, Тео; Перре, Людовик; Саката, Сёдзиро; Траверсо, Карло (ред.). Базы Грёбнера, кодирование и криптография . Springer Science & Business Media . п. 220 . ISBN 978-3-540-93806-4 .

[Hazewinkel-Sole_2016-90] Соле, Патрик (2016). «Коды Кердока и Препарата» . В Хазевинкеле, Михил (ред.). Энциклопедия математики . Springer Science+Business Media . ISBN 978-1-4020-0609-8 . Архивировано из оригинала 29 октября 2017 г.

[Spaulding_1965-91] Сполдинг, Карл П. (12 июля 1965 г.). Как использовать энкодеры вала . Монровия, Калифорния, США: Datex Corporation. (85 страниц)

[Wheeler_1969-92] Jump up to: ^а ^б Уиллер, Эдвин Л. (30 декабря 1969 г.) [5 апреля 1968 г.]. Аналого-цифровой кодер (PDF) . Нью-Йорк, США: Корпорация Conrac. Патент США 3487460А . Серийный № 719026 (397812). Архивировано (PDF) из оригинала 5 августа 2020 г. Проверено 21 января 2018 г. п. 5, левый столбец 9, строки 15–22: […] Код MOA-GILLHAM по существу представляет собой комбинацию обсуждавшегося выше кода Грея и хорошо известного кода Datex ; код Datex раскрыт в патенте США 3165731 . Схема такова, что код Datex определяет биты для подсчета единиц кодера, а код Грея определяет биты для каждого из декад более высокого порядка, десятков, сотен и т. д. […] (11 страниц)

[Dokter-Steinhauer_1973-93] Jump up to: ^а ^б ^с ^д ^и ^ж Доктер, Фолкерт; Штайнхауэр, Юрген (18 июня 1973 г.). «2.4. Кодирование чисел в двоичной системе». Цифровая электроника . Техническая библиотека Philips (PTL) / Macmillan Education (переиздание 1-го изд. на английском языке). Эйндховен, Нидерланды: The Macmillan Press Ltd. / Gloeilampenfabrieken NV Philips . стр. 32, 39, 50–53. дои : 10.1007/978-1-349-01417-0 . ISBN 978-1-349-01419-4 . СБН 333-13360-9 . Проверено 11 мая 2020 г. п. 53: […] Код Datex […] использует код О'Брайена II в пределах каждого десятилетия и отражает десятичные числа для десятичных переходов. Для дальнейшей обработки необходимо преобразование кода в естественную десятичную систему счисления. Поскольку код О'Брайена II образует дополнение до девяток , это не вызывает особых трудностей: всякий раз, когда кодовое слово для десятков представляет собой нечетное число, кодовые слова для десятичных единиц задаются как дополнения до девяток путем инверсии числа. четвертая двоичная цифра. […] ^{[ постоянная мертвая ссылка ]} (270 страниц)

[Dokter-Steinhauer_1975-94] Jump up to: ^а ^б ^с ^д ^и Доктер, Фолкерт; Штайнхауэр, Юрген (1975) [1969]. «2.4.4.6. Одношаговые коды». Цифровая электроника в измерительной технике и обработке данных: Теоретические основы и схемотехника . Специализированные книги Philips (на немецком языке). Том I (улучшенное и расширенное 5-е изд.). Гамбург, Германия: Deutsche Philips GmbH . С. 41, 48, 51, 58, 60–61. ISBN 3-87145-272-6 . (xii+327+3 страницы)

[Varec_1954-95] «…точное измерение уровня жидкости – на ЛЮБОМ РАССТОЯНИИ!» . Нефтеперерабатывающий завод (Реклама). 33 (9). Gulf Publishing Company : 368. Сентябрь 1954 г. ISSN 0096-6517 . п. 368: […] Полная диспетчеризация, измерение и дистанционное управление интегрированы в одну единую систему, когда установлена система телеметрии с импульсно-кодовым кодом «Varec». […]

[Bishup-Repeta-Giarrizzo_1963-96] Бишуп, Бернард В.; Репета, Энтони А.; Джарриццо, Фрэнк К. (13 августа 1968 г.) [3 апреля 1963 г.]. «Система телеизмерения и диспетчерского управления, имеющая обычно непрерывные телеметрические сигналы» . Лидс и Нортруп Ко. US3397386A. [11]

[Whessoe_1993-97] «Формат импульса кодировщика». Руководство по установке и эксплуатации 4-проводного микропередатчика модели 1900 (PDF) . Сайпресс, Калифорния, США: Whessoe Varec, Inc. , январь 1993 г. [1991-07-01]. стр. 04-4–04-8. 33-08461. Архивировано (PDF) из оригинала 16 мая 2020 г. Проверено 16 мая 2020 г. (38 страниц) (Примечание. В позиции 5 для «Дюймов» на стр. 04–8 следует читать «0111», а не «1111».)

[Emerson-98] «2.2.3.3 Формат данных уровня MSP». Varec Model 1900 — 4-проводной микропередатчик (протокол BSAP — Mark/Space (MSP)) — Замечания по применению (PDF) . Эмерсон Электрик . стр. 11–14. Архивировано (PDF) из оригинала 16 мая 2020 г. Проверено 16 мая 2020 г. (vi+33 страницы)

[Wightman_1972-100] Jump up to: ^а ^б ^с Вайтман, Эрик Джеффри (1972). «Глава 6. Измерение смещения» . Приборы в управлении технологическими процессами (1-е изд.). Лондон, Великобритания: Butterworth & Co (Publishers) Ltd. стр. 122–123. ISBN 0-408-70293-1 . п. 122–123: […] Другие формы кода также хорошо известны. Среди них кодекс Королевского радиолокационного учреждения ; Десятичный код лишних трех ; Код Гиллхэма , рекомендованный ИКАО для автоматической передачи данных о высоте для управления воздушным движением целей ; код Петерика и код Лесли и Рассела Национальной инженерной лаборатории . Каждый из них имеет свои преимущества и предлагается в качестве опции различными производителями кодеров. […] (12+367+5 страниц)

[Phillips_1998-101] Филлипс, Дэррил (26 июля 2012 г.) [1998]. «Высота – МОДЕК ASCII» . Авионика ЭйрСпорт. Архивировано из оригинала 26 июля 2012 г.

[Stewart_2010-102] Стюарт, К. (3 декабря 2010 г.). «Код авиационного Грея: объяснение кода Гиллхэма» . Пользовательские компьютерные услуги (CCS). Архивировано из оригинала 16 января 2018 г. Проверено 14 января 2018 г.

[Leslie-Russell_1964-103] Лесли, Уильям «Билл» HP; Рассел, А. (1964). Циклический прогрессивный десятичный код для простого перевода в десятичные и аналоговые выходные данные (Отчет). Ист-Килбрайд, Глазго, Великобритания: Национальная инженерная лаборатория . Отчет NEL 129. (17 страниц)

[Leslie_1974-104] Лесли, Уильям «Билл» HP (1974). «Работа над NC в НЭЛ» . В Кенигсбергере, Франц; Тобиас, Стивен Альберт (ред.). Материалы четырнадцатой Международной конференции по проектированию и исследованию станков, 12–14 сентября 1973 г. Макмиллан Пресс Лтд . С. 215–224 [215, 217]. дои : 10.1007/978-1-349-01921-2_30 . ISBN 978-1-34901921-2 . LCCN 73-16545 . СБН 333-14913-0 . Архивировано из оригинала 7 апреля 2022 г. Проверено 21 мая 2020 г.

[Hoklas_1989-105] Хоклас, Арчибальд (6 сентября 1989 г.) [29 апреля 1988 г.]. «Сканирующее устройство для цифрового измерения расстояния или угла» (PDF) (на немецком языке). VEB Schiffselektronik Йоханнес Варнке [ де ] . Патент ГДР DD271603A1. WP H 03 M / 315 194 8. Архивировано из оригинала (PDF) 18 января 2018 г. Проверено 18 января 2018 г. - через DEPATIS [ de ] . [12] [13]

[Hoklas_2005_1-106] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к Хоклас, Арчибальд (2005). «Код Грея – Код единичного расстояния» . Архивировано из оригинала 15 января 2018 г. Проверено 15 января 2018 г.

[Hoklas_2005_2-107] Jump up to: ^а ^б ^с ^д ^и Хоклас, Арчибальд (2005). «Код Грея – код одношаговой выборки» (на немецком языке). Архивировано из оригинала 15 января 2018 г. Проверено 15 января 2018 г.

[Petherick-Hopkins_1958-108] Петерик, Эдвард Джон; Хопкинс, Эй Джей (1958). Некоторые недавно разработанные цифровые устройства для кодирования вращения валов (Техническая нота MS21). Фарнборо, Великобритания: Королевское авиастроительное предприятие (RAE).

[Baumgartner_1963-109] «Дигитайзер как аналого-цифровой преобразователь в технике управления, измерения и регулирования» (PDF) . Технические уведомления . Реле, электронные устройства, органы управления (на немецком языке). Нет. 13. Кёльн-Ниль, Германия: Франц Баумгартнер (FraBa). Май 1963 г., стр. 1–2. Архивировано из оригинала (PDF) 21 мая 2020 г. Проверено 21 мая 2020 г. стр. 1-2: [...] Компания Harrison Reproduction Equipment, Фарнборо/Англия [...], за годы разработок в сотрудничестве с британскими ВВС и британскими промышленными компаниями, представила механический дигитайзер [.. .] до технической зрелости, отвечающей почти всем требованиям […], достаточно. […] Чтобы добиться четких результатов при расшифровке десятичного используемого двоичного кода и всегда получать правильные результаты при переходе от одного десятичного знака к другому в порядке, был разработан специальный код, который по своему принципу исключает всякую возможность неправильного высказываний и который также характеризуется: его структура допускает относительно легкую расшифровку. На этом основан код Петерик-Код . […] (4 страницы)

[Charnley-Bidgood-Boardman_1965-110] Jump up to: ^а ^б Чарнли, CJ; Бидгуд, RE; Бордман, GET (октябрь 1965 г.). «Конструкция пневматического энкодера положения» (PDF) . Тома трудов МФБ . 2 (3). Колледж аэронавтики, Крэнфилд, Бедфорд, Англия: 75–88. дои : 10.1016/S1474-6670(17)68955-9 . Глава 1.5 . Проверено 14 января 2018 г. ^{[ постоянная мертвая ссылка ]}

[Hollingdale_1958-112] Холлингдейл, Стюарт Х. (19 сентября 1958 г.). «Сессия 14. Обработка данных» . Применение компьютеров (доклад конференции). Атлас – Применение компьютеров, Ноттингемский университет, 15–19 сентября 1958 г. Архивировано из оригинала 25 мая 2020 г. Проверено 25 мая 2020 г.

[O'Brien_1955-113] Jump up to: ^а ^б ^с О'Брайен, Джозеф А. (май 1956 г.) [15 ноября 1955 г., 23 июня 1955 г.]. «Циклические десятичные коды для аналого-цифровых преобразователей» . Труды Американского института инженеров-электриков, Часть I: Связь и электроника . 75 (2). Bell Telephone Laboratories, Уиппани, Нью-Джерси, США: 120–122. дои : 10.1109/TCE.1956.6372498 . ISSN 0097-2452 . S2CID 51657314 . Документ 56-21. Архивировано из оригинала 18 мая 2020 г. Проверено 18 мая 2020 г. (3 страницы) (Примечание. Этот документ был подготовлен для презентации на Зимнем общем собрании AIEE, Нью-Йорк, США, с 30 января 1956 г. по 3 февраля 1956 г.)

[Steinbuch_1962-114] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Штайнбух, Карл В. , изд. Написано в Карлсруэ, Германия. Обработка сообщений в мягкой обложке (на немецком языке) (1-е изд.). Берлин / Геттинген / Нью-Йорк: Springer-Verlag OHG . стр. 71–74, 97, 761–764, 770, 1080–1081. LCCN 62-14511 .

[Steinbuch-Weber-Heinemann_1974-115] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Штайнбух, Карл В .; Вебер, Вольфганг; Хайнеманн, Трауте, ред. (1974) [1967]. Карманный справочник по информатике - Том II - Структура и программирование компьютерных систем . Обработка сообщений в мягкой обложке (на немецком языке). Том 2 (3-е изд.). Берлин, Германия: Springer Verlag . стр. 98–100. ISBN 3-540-06241-6 . LCCN 73-80607 .

[Foss_1954_1-117] Фосс, Фредерик А. (27 декабря 1960 г.) [17 декабря 1954 г.]. «Системы управления» (PDF) . Международная Бизнес Машинная Корпорация . Рис. 7, Рис. 8, Рис. 11. Патент США 2966670А . Серийный номер 475945. Архивировано (PDF) из оригинала 21 июня 2020 г. Проверено 5 августа 2020 г. (14 страниц) (Примечание. Автор назвал свой код 2*-4-2-1 (+9-±7-±3-±1), отраженный десятичный код.)

[Foss_1954_2-118] Фосс, Фредерик А. (декабрь 1954 г.). «Использование отраженного кода в цифровых системах управления». IRE-транзакции на электронных компьютерах . ИК-3 (4): 1–6. дои : 10.1109/IREPGELC.1954.6499244 . ISSN 2168-1740 . (6 страниц)

[Evans_1958-119] Эванс, Дэвид Сильвестр (1958). «[название неизвестно]» . Транзакции . 10–12. Институт измерения и контроля: 87. (Примечание. Код Уоттса назывался кодом WRD или Watts Reflected Decimal, чтобы отличать его от других кодов, используемых в Hilger & Watts Ltd. )

[Benjamin-Nicholls_1963-120] Бенджамин, PW; Николлс, GS (1963). «3.2.2 Электромеханические цифровые преобразователи» . Измерение спектров нейтронов методом полуавтоматического сканирования протонов отдачи в фотоэмульсиях . Управление по атомной энергии Соединенного Королевства , Научно-исследовательский центр по атомному оружию , Великобритания: Министерство энергетики США . стр. 8–10, 19. Отчет AWRE № NR 5/63. [14] (23 страницы)

[Klinkowski_1964-121] Клинковски, Джеймс Дж. (14 марта 1967 г.) [23 марта 1964 г.]. «Схемы электронного диодно-матричного декодера» (PDF) . Детройт, Мичиган, США: Корпорация Берроуз . Патент США 3309695А . Серийный номер 353845. Архивировано (PDF) из оригинала 23 мая 2020 г. Проверено 23 мая 2020 г. (5 страниц) [15]

[Klinkowski_1966-122] Клинковски, Джеймс Дж. (31 марта 1970 г.) [22 декабря 1966 г.]. «Преобразователь двоично-десятичных сигналов» (PDF) . Детройт, Мичиган, США: Корпорация Берроуз . Патент США 3504363А . Серийный номер 603926. Архивировано (PDF) из оригинала 23 мая 2020 г. Проверено 23 мая 2020 г. (7 страниц)

[EDN_1967-123] «[название неизвестно]». Новости электротехнического проектирования . 12 . Издательская компания Роджерс . 1967. ISSN 0012-7515 . [16] [17]

[Toth-Zentai_1979-124] Тот-Зентаи, Дьёрдьи (05.10.1979). «Некоторые проблемы углово-вращательных цифровых преобразователей» . Периодика Политехника Электротехника . 23 (3–4). Кафедра электронных технологий, Технический университет, Будапешт, Венгрия: 265–270 [266] . Проверено 23 мая 2020 г. [18] (6 страниц) (Примечание. Показывает 6-значный код Уоттса.)

[Savard_2018-125] Савард, Джон Дж. Г. (2018) [2006]. «Десятичные представления» . четырехблок . Архивировано из оригинала 16 июля 2018 г. Проверено 16 июля 2018 г.

[Turvey_1956-126] Jump up to: ^а ^б Терви-младший, Фрэнк П. (29 июля 1958 г.) [17 мая 1956 г.]. «Кодер подсчета импульсов» (PDF) . Натли, Нью-Джерси, США: Международная телефонная и телеграфная корпорация . Патент США 2845617А . Серийный номер 585494. Архивировано (PDF) из оригинала 23 мая 2020 г. Проверено 23 мая 2020 г. (5 страниц)

[Glixon_1957-127] Jump up to: ^а ^б Гликсон, Гарри Роберт (март 1957 г.). «Можете ли вы воспользоваться преимуществами циклического двоично-десятичного кода?» . Техника управления . 4 (3). Техническая издательская компания , подразделение издательской корпорации Dun-Donnelley, Dun & Bradstreet Corp .: 87–91. ISSN 0010-8049 . (5 страниц)

[Borucki-Dittmann_1971-128] Jump up to: ^а ^б Боруки, Лоренц; Диттманн, Иоахим (1971) [июль 1970, 1966, осень 1965]. «2.3 Общие коды в цифровой измерительной технике». Написано в Крефельде/Карлсруэ, Германия. Технология цифровых измерений: Введение (на немецком языке) (2-е изд.). Берлин / Гейдельберг, Германия: Springer-Verlag . С. 10–23 [12–14]. дои : 10.1007/978-3-642-80560-8 . ISBN 3-540-05058-2 . LCCN 75-131547 . ISBN 978-3-642-80561-5 . (viii+252 страницы) 1-е издание (Примечание. Как и Каммерер , авторы описывают 6-битный 20-циклический код Гликсона.)

[Kämmerer_1969-129] Jump up to: ^а ^б Каммерер, Вильгельм [на немецком языке] (май 1969 г.). «II.15. Структура: Представление информации в автомате». Написано в Йене, Германия. Во Фрюхауфе, Ганс [на немецком языке] ; Чемберлен, Вильгельм; Шредер, Курц; Винклер, Хельмут (ред.). Цифровые автоматы – теория, структура, технология, программирование . Электронные вычисления и правила (на немецком языке). Том 5 (1-е изд.). Берлин, Германия: Akademie-Verlag GmbH . п. 173. Лицензия № 202-100/416/69. Заказ № 4666 ES 20 K 3. (Примечание. Существует также второе издание 1973 года. Подобно Боруки и Диттманну , но не называя его кодом Гликсона, автор создает 20-циклический тетрадный код из кода Гликсона и вариант кода Гликсона с инвертированный старший бит.)

[Paul_1995-133] Пол, Матиас Р. (10 августа 1995 г.) [1994]. «Unterbrechungsfreier Schleifencode» [Код непрерывного цикла]. 1.02 (на немецком языке) . Проверено 11 февраля 2008 г. (Примечание. Автор назвал этот код Schleifencode (англ. «код цикла»). Он отличается от кода Грея BCD только кодированием состояния 0, что делает его циклическим кодом единичного расстояния для приложений с полным круговым вращением. Избегание всех -нулевой шаблон кода позволяет выполнять самотестирование контура и использовать линии передачи данных для бесперебойного распределения электроэнергии.)

[Klar_1970-135] Конечно, Райнер (1 февраля 1970 г.). Введение – Цифровые компьютеры Коллекция Гёшена (на немецком языке). Том 1241/1241а (1-е изд.). Берлин, Германия: Вальтер де Грюйтер и компания / GJ Göschen'sche Verlagsbuchhandlung [ de ] . п. 17. ISBN 3-11-083160-0 . . Архив-Nr. 7990709. Архивировано из оригинала 1 июня 2020 г. Проверено 13 апреля 2020 г. (205 страниц) (Примечание. Перепечатка первого издания за 2019 год доступна по ссылке ISBN 3-11002793-3 , 978-3-11002793-8 . переработанное и расширенное 4-е издание .) Также существует

[Klar_1989-136] Конечно, Райнер (1989) [1988-10-01]. компьютеры – Введение в структуру компьютерного оборудования Цифровые . Коллекция Гёшена (на немецком языке). Том 2050 (4-е переработанное изд.). Берлин, Германия: Walter de Gruyter & Co. 28. ISBN 3-11011700-2 . (320 страниц) (Примечание. Автор назвал этот код Einheitsabstandscode (англ. «код единичного расстояния»). Поменяв местами две битовые строки и инвертировав одну из них, его можно перевести в код О'Брайена II , тогда как поменяв местами и инвертировав две битовые строки, его можно перевести в код Петерика .)

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ 28 ]

[ 29 ]

[ 30 ]

[ 31 ]

[ 32 ]

[ 33 ]

[ 34 ]

[ 35 ]

[ 36 ]

[ 37 ]

[ 38 ]

[ 39 ]

[ 40 ]

[ 41 ]

[ 42 ]

[ 43 ]

[ 44 ]

[ 45 ]

[ 46 ]

[ 47 ]

[ 48 ]

[ 49 ]

[ 50 ]

[ 51 ]

[ 52 ]

[ 53 ]

[ номер 1 ]

[ 54 ]

[ 55 ]

[ 56 ]

[ 57 ]

[ 58 ]

[ 59 ]

[ номер 2 ]

[ 60 ]

[ 61 ]

[ 62 ]

[ 63 ]

[ 64 ]

[ 65 ]

[ 66 ]

[ 67 ]

[ 68 ]

[ 69 ]

[ 70 ]

[ 71 ]

[ 72 ]

[ 73 ]

[ 74 ]

[ 75 ]

[ 76 ]

[ 77 ]

[ 78 ]

[ 79 ]

[ 80 ]

[ 81 ]

[ 82 ]

[ 83 ]

[ 84 ]

[ 85 ]

[ 86 ]

[ 87 ]

[ 88 ]

[ 89 ]

[ 90 ]

[ 91 ]

[ 92 ]

[ 93 ]

[ 94 ]

[ 95 ]

[ 96 ]

[ номер 3 ]

[ 97 ]