Прямой угол


| Виды углов |
|---|
| 2D углы |
| сферический |
| 2D пары углов |
Соседний |
| 3D углы |
| Твердый |
В геометрии и тригонометрии называется прямым углом угол , равный ровно 90 градусам или / 2 радиана [1] соответствует четверти оборота . [2] Если луч расположен так, что его конец лежит на прямой и прилежащие к нему углы равны, то они прямые. [3] Этот термин калькой латинского angulusrectus является ; здесь прямая мышца означает «вертикальная», имея в виду вертикаль, перпендикулярную горизонтальной базовой линии.
Тесно связанными и важными геометрическими понятиями являются перпендикулярные линии, то есть линии, образующие прямые углы в точке пересечения, и ортогональность , которая является свойством образования прямых углов, обычно применяемым к векторам . Наличие прямого угла в треугольнике является определяющим фактором для прямоугольных треугольников . [4] сделать прямой угол основой тригонометрии.
Этимология [ править ]
Значение слова «прямо под прямым углом», возможно, отсылает к латинскому прилагательному «прямой» , «прямой, прямой, вертикальный, перпендикулярный». Греческий « эквивалент — ортос » «прямой»; перпендикуляр» (см. ортогональность ).
В элементарной геометрии [ править ]
Прямоугольник – это четырехугольник с четырьмя прямыми углами. есть квадрата Помимо сторон равной длины, у четыре прямых угла.
Теорема Пифагора гласит, как определить, является ли треугольник прямоугольным .
Символы [ править ]

В Юникоде символ прямого угла — U+221F ∟ ПРАВЫЙ УГОЛ ( &ангрт; ). Его не следует путать с символом аналогичной формы. U + 231E ⌞ НИЖНИЙ ЛЕВЫЙ УГОЛ ( ⌞, ⌞ ). Связанные символы: U+22BE ⊾ ПРЯМОЙ УГОЛ С ДУГОЙ ( ⊾ ), U + 299C ⦜ ПРЯМОУГОЛЬНЫЙ ВАРИАНТ С КВАДРАТОМ ( &вангрт; ), и U+299D ⦝ ИЗМЕРЕН ПРЯМОЙ УГОЛ С ТОЧКОЙ ( ⦝ ). [5]
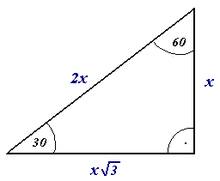
На диаграммах тот факт, что угол является прямым, обычно выражается добавлением небольшого прямого угла, который образует квадрат с углом на диаграмме, как это видно на диаграмме прямоугольного треугольника (в британском английском - прямоугольный угол). треугольник) вправо. Символ измеренного угла, дуга с точкой, используется в некоторых европейских странах, включая немецкоязычные страны и Польшу, как альтернативный символ прямого угла. [6]
Евклид [ править ]
Прямые углы имеют основополагающее значение в «Началах» Евклида . Они определены в Книге 1, определении 10, где также определяются перпендикулярные линии. Определение 10 не использует числовые измерения в градусах, а скорее затрагивает самую суть того, что такое прямой угол, а именно две прямые линии, пересекающиеся, образующие два равных и смежных угла. [7] Прямые, образующие прямые углы, называются перпендикулярами. [8] Евклид использует прямые углы в определениях 11 и 12 для определения острых углов (меньших прямого угла) и тупых углов (больше прямого угла). [9] Два угла называются дополнительными , если их сумма является прямым углом. [10]
Постулат 4 книги 1 гласит, что все прямые углы равны, что позволяет Евклиду использовать прямой угол как единицу измерения других углов. Комментатор Евклида Прокл дал доказательство этого постулата, используя предыдущие постулаты, но можно утверждать, что это доказательство использует некоторые скрытые предположения. Саккери также дал доказательство, но использовал более явное предположение. В это Гильберта аксиоматизации геометрии утверждение дано в виде теоремы, но только после долгой подготовки. Можно возразить, что, даже если постулат 4 может быть доказан на основе предыдущих, в том порядке, в котором Евклид излагает свой материал, его необходимо включить, поскольку без него постулат 5, использующий прямой угол в качестве единицы измерения, не имеет никакого значения. смысл. [11]
Преобразование в другие единицы [ править ]
Прямой угол может выражаться в разных единицах:
- 1/4 оборота
- 90° ( градусов )
- π / 2 радиан
- 100 град (также называемый градусом , градианом или гоном )
- 8 баллов (из 32-точечной розы компаса )
- 6 часов (астрономический часовой угол )
Правило 3-4-5 [ править ]
На протяжении всей истории плотники и каменщики знали быстрый способ проверить, является ли угол прямым. В его основе лежит пифагорейская тройка (3, 4, 5) и правило 3-4-5. Проведение прямой линии от рассматриваемого угла вдоль одной стороны длиной ровно три единицы, а вдоль второй стороны длиной ровно четыре единицы создаст гипотенузу ( более длинную линию, противоположную прямому углу, который соединяет две измеренные конечные точки) ровно пять единиц длины.
Теорема Фалеса [ править ]
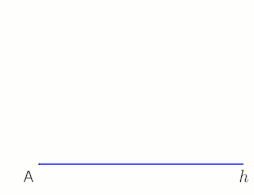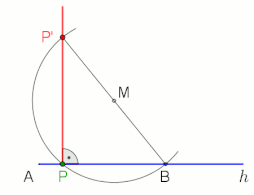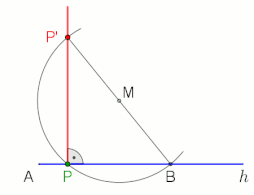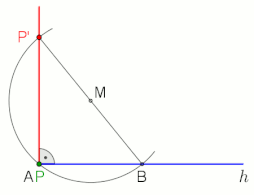
Теорема Фалеса утверждает, что угол, вписанный в полукруг (с вершиной полукруга и ее определяющими лучами, проходящими через конечные точки полукруга), является прямым углом.
Два примера применения, в которые включены прямой угол и теорема Фалеса (см. Анимацию).
См. также [ править ]
Ссылки [ править ]
- ^ «Прямой угол» . Открытый справочник по математике . Проверено 26 апреля 2017 г. .
- ^ Вентворт с. 11
- ^ Вентворт с. 8
- ^ Вентворт с. 40
- ^ Таблицы кодов символов Unicode 5.2. Математические операторы , разные математические символы-B
- ^ Мюллер-Филипп, Сюзанна; Горский, Ханс Иоахим (2011). Справочник по геометрии . (на немецком языке) Спрингер. ISBN 9783834886163 .
- ^ Хит стр. 181
- ^ Хит стр. 181
- ^ Хит стр. 181
- ^ Вентворт с. 9
- ^ Хит, стр. 200–201 для абзаца.
- Вентворт, Джорджия (1895 г.). Учебник геометрии . Джинн и Ко.
- Евклид, комментарии и пер. от TL Heath Elements Vol. 1 (Кембридж, 1908 г.) Google Книги