Ортоптика (геометрия)

Чтобы узнать об отрасли медицины, см. Ортоптика .

В геометрии кривых касательные ортоптика — это набор точек, в которых две данной кривой пересекаются под прямым углом.

  Парабола

  Ортоптика параболы (ее директрисы )

  Эллипс

  Ортоптика эллипса (его направляющий круг )

  Минимальная ограничивающая рамка эллипса ( описанного ортоптической окружностью)

  Большая и малая оси эллипса

  Гипербола

  Ортоптика гиперболы (ее направляющий круг)

  xy -оси и гиперболические асимптоты

Примеры:

1. Ортоптиком параболы является ее директриса (доказательство: см. ниже ),
2. Ортоптика эллипса ${\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ это режиссерский круг $x^{2}+y^{2}=a^{2}+b^{2}$ (см. ниже ),
3. Ортоптика гиперболы ${\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1,\ a>b$ это режиссерский круг $x^{2}+y^{2}=a^{2}-b^{2}$ (в случае a ≤ b нет ортогональных касательных, см. ниже ),
4. Ортоптика астроиды $x^{2/3}+y^{2/3}=1$ представляет собой четырехлистник с полярным уравнением $r={\tfrac {1}{\sqrt {2}}}\cos(2\varphi ),\ 0\leq \varphi <2\pi$ (см. ниже ).

Обобщения:

1. Изоптика — это набор точек, в которых две касательные данной кривой пересекаются под фиксированным углом (см. ниже ).
2. Изоптика плоских кривых — двух фиксированным это набор точек, в которых две касательные пересекаются под углом .
3. Теорему Фалеса об хорде PQ можно рассматривать как ортоптику двух окружностей, вырожденных в две P и Q. точки

Ортоптика параболы

(углы не изменяются) превратить Любую параболу можно жестким движением в параболу с уравнением $y=ax^{2}$. Наклон в точке параболы равен $m=2ax$. Замена x дает параметрическое представление параболы с наклоном касательной в качестве параметра: $\left({\tfrac {m}{2a}},{\tfrac {m^{2}}{4a}}\right)\!.$ Тангенс имеет уравнение $y=mx+n$ с пока неизвестным n , которое можно определить, подставив координаты точки параболы. Получаешь $y=mx-{\tfrac {m^{2}}{4a}}\;.$

Если касательная содержит точку ( x ₀ , y ₀ ) вне параболы, то уравнение $$y_{0}=mx_{0}-{\frac {m^{2}}{4a}}\quad \rightarrow \quad m^{2}-4ax_{0}\,m+4ay_{0}=0$$имеет место, которое имеет два решения m ₁ и m _2, соответствующие двум касательным, проходящим ( x ₀ , y ₀ ) . Свободный член приведенного квадратного уравнения всегда является произведением его решений. Следовательно, если касательные пересекаются в точке ( x ₀ , y ₀ ) ортогонально, выполняются следующие уравнения: $$m_{1}m_{2}=-1=4ay_{0}$$Последнее уравнение эквивалентно $$y_{0}=-{\frac {1}{4a}}\,,$$что является уравнением директрисы .

Ортоптика эллипса и гиперболы.

Эллипс

Основная статья: Режиссерский круг

Позволять $E:\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1$ быть эллипсом рассмотрения.

1. Касательные к эллипсу $E$ в вершинах и ко-вершинах пересекаются в 4 точках $(\pm a,\pm b)$, лежащие на искомой ортоптической кривой (окружности $x^{2}+y^{2}=a^{2}+b^{2}$).
2. Касательная в точке $(u,v)$ эллипса $E$ имеет уравнение ${\tfrac {u}{a^{2}}}x+{\tfrac {v}{b^{2}}}y=1$ (см. касательную к эллипсу ). Если точка не является вершиной, это уравнение можно решить относительно y : $y=-{\tfrac {b^{2}u}{a^{2}v}}\;x\;+\;{\tfrac {b^{2}}{v}}\,.$

Использование сокращений

$${\begin{aligned}m&=-{\tfrac {b^{2}u}{a^{2}v}},\\\color {red}n&=\color {red}{\tfrac {b^{2}}{v}}\end{aligned}}$$ ( я )

и уравнение ${\color {blue}{\tfrac {u^{2}}{a^{2}}}=1-{\tfrac {v^{2}}{b^{2}}}=1-{\tfrac {b^{2}}{n^{2}}}}$ человек получает: $$m^{2}={\frac {b^{4}u^{2}}{a^{4}v^{2}}}={\frac {1}{a^{2}}}{\color {red}{\frac {b^{4}}{v^{2}}}}{\color {blue}{\frac {u^{2}}{a^{2}}}}={\frac {1}{a^{2}}}{\color {red}n^{2}}{\color {blue}\left(1-{\frac {b^{2}}{n^{2}}}\right)}={\frac {n^{2}-b^{2}}{a^{2}}}\,.$$Следовательно

$$n=\pm {\sqrt {m^{2}a^{2}+b^{2}}}$$ ( II )

и уравнение невертикальной касательной: $$y=mx\pm {\sqrt {m^{2}a^{2}+b^{2}}}.$$Решение соотношений (I) для $u,v$ и соблюдение (II) приводит к параметрическому представлению эллипса, зависящему от наклона: $$(u,v)=\left(-{\tfrac {ma^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\;,\;{\tfrac {b^{2}}{\pm {\sqrt {m^{2}a^{2}+b^{2}}}}}\right)\,.$$ (Другое доказательство: см. Эллипс § Параметрическое представление .)

Если касательная содержит точку $(x_{0},y_{0})$, вне эллипса, то уравнение $$y_{0}=mx_{0}\pm {\sqrt {m^{2}a^{2}+b^{2}}}$$держит. Устранение квадратного корня приводит к $$m^{2}-{\frac {2x_{0}y_{0}}{x_{0}^{2}-a^{2}}}m+{\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}=0,$$который имеет два решения $m_{1},m_{2}$ соответствующие двум касательным, проходящим через $(x_{0},y_{0})$. Постоянный член квадратного уравнения всегда является произведением его решений. Следовательно, если касательные пересекаются в точке $(x_{0},y_{0})$ ортогонально имеют место следующие уравнения:

Ортоптика (красные круги) круга, эллипсов и гипербол.

$$m_{1}m_{2}=-1={\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}$$Последнее уравнение эквивалентно $$x_{0}^{2}+y_{0}^{2}=a^{2}+b^{2}\,.$$Из (1) и (2) получаем:

Точки пересечения ортогональных касательных являются точками окружности. $x^{2}+y^{2}=a^{2}+b^{2}$.

Гипербола

Случай эллипса можно почти точно адаптировать к случаю гиперболы. Единственные изменения, которые необходимо внести, это заменить $b^{2}$ с $-b^{2}$ и ограничить m до | м | > ⁠ б / а ⁠ . Поэтому:

Точки пересечения ортогональных касательных являются точками окружности. $x^{2}+y^{2}=a^{2}-b^{2}$, где а > b .

Ортоптика астроиды

Ортоптический (фиолетовый) астроиды

Астроид можно описать параметрическим представлением $$\mathbf {c} (t)=\left(\cos ^{3}t,\sin ^{3}t\right),\quad 0\leq t<2\pi .$$Из условия $$\mathbf {\dot {c}} (t)\cdot \mathbf {\dot {c}} (t+\alpha )=0$$можно распознать расстояние α в пространстве параметров, на котором появляется ортогональная касательная к ċ ( t ) . Оказывается, расстояние не зависит от параметра t , а именно α = ± ⁠ π / 2 ⁠ . Уравнения (ортогональных) касательных в точках c ( t ) и c ( t + ⁠ π / 2 ⁠ ) соответственно: $${\begin{aligned}y&=-\tan t\left(x-\cos ^{3}t\right)+\sin ^{3}t,\\y&={\frac {1}{\tan t}}\left(x+\sin ^{3}t\right)+\cos ^{3}t.\end{aligned}}$$Их общая точка имеет координаты: $${\begin{aligned}x&=\sin t\cos t\left(\sin t-\cos t\right),\\y&=\sin t\cos t\left(\sin t+\cos t\right).\end{aligned}}$$Это одновременно параметрическое представление ортоптики.

Исключение параметра t дает неявное представление $$2\left(x^{2}+y^{2}\right)^{3}-\left(x^{2}-y^{2}\right)^{2}=0.$$Вводя новый параметр φ = t − ⁠ 5π / 4 ⁠ получается $${\begin{aligned}x&={\tfrac {1}{\sqrt {2}}}\cos(2\varphi )\cos \varphi ,\\y&={\tfrac {1}{\sqrt {2}}}\cos(2\varphi )\sin \varphi .\end{aligned}}$$(В доказательстве используются тождества угловой суммы и разности .) Следовательно, мы получаем полярное представление $$r={\tfrac {1}{\sqrt {2}}}\cos(2\varphi ),\quad 0\leq \varphi <2\pi$$ из ортоптики. Следовательно:

Ортоптика астроиды — четырехлистный .

Изоптика параболы, эллипса и гиперболы.

Изоптика (фиолетовая) параболы для углов 80° и 100°.

Изоптика (фиолетовая) эллипса для углов 80° и 100°.

Изоптика (фиолетовая) гиперболы для углов 80° и 100°.

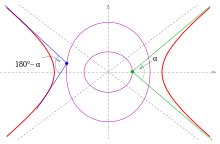
изотопы для углов α ≠ 90° Ниже перечислены . Их называют α -изоптиками. Доказательства см. ниже .

Уравнения изоптики

Парабола:

α - изоптика параболы с уравнением y = ax ² являются ветвями гиперболы $$x^{2}-\tan ^{2}\alpha \left(y+{\frac {1}{4a}}\right)^{2}-{\frac {y}{a}}=0.$$Ветви гиперболы образуют изоптику для двух углов α и 180° − α (см. рисунок).

Эллипс:

α - изоптика эллипса с уравнением ⁠ x ² / а ² ⁠ + ⁠ y ² / б ² ⁠ = 1 — две части кривой 4-й степени. $$\left(x^{2}+y^{2}-a^{2}-b^{2}\right)^{2}\tan ^{2}\alpha =4\left(a^{2}y^{2}+b^{2}x^{2}-a^{2}b^{2}\right)$$(см. картинку).

Гипербола:

α - изоптика гиперболы с уравнением ⁠ x ² / а ² ⁠ − ⁠ y ² / б ² ⁠ = 1 — две части кривой 4-й степени. $$\left(x^{2}+y^{2}-a^{2}+b^{2}\right)^{2}\tan ^{2}\alpha =4\left(a^{2}y^{2}-b^{2}x^{2}+a^{2}b^{2}\right).$$

Доказательства

Парабола:

Парабола y = ax ² может быть параметризован наклоном его касательных m = 2 ax : $$\mathbf {c} (m)=\left({\frac {m}{2a}},{\frac {m^{2}}{4a}}\right),\quad m\in \mathbb {R} .$$

Касательная с наклоном m имеет уравнение $$y=mx-{\frac {m^{2}}{4a}}.$$

Точка ( x ₀ , y ₀ ) находится на касательной тогда и только тогда, когда $$y_{0}=mx_{0}-{\frac {m^{2}}{4a}}.$$

Это означает, что наклоны m ₁ , m ₂ двух касательных, содержащих ( x ₀ , y ₀ ), удовлетворяют квадратному уравнению $$m^{2}-4ax_{0}m+4ay_{0}=0.$$

Если касательные пересекаются под углом α или 180° − α , уравнение $$\tan ^{2}\alpha =\left({\frac {m_{1}-m_{2}}{1+m_{1}m_{2}}}\right)^{2}$$

должно быть выполнено. Решив квадратное уравнение для m и подставив m ₁ , m ₂ в последнее уравнение, получим $$x_{0}^{2}-\tan ^{2}\alpha \left(y_{0}+{\frac {1}{4a}}\right)^{2}-{\frac {y_{0}}{a}}=0.$$

Это уравнение гиперболы, приведенной выше. Его ветви несут две изоптики параболы для двух углов α и 180° − α .

Эллипс:

В случае эллипса ⁠ x ² / а ² ⁠ + ⁠ y ² / б ² ⁠ = 1 можно принять идею ортоптики квадратного уравнения $$m^{2}-{\frac {2x_{0}y_{0}}{x_{0}^{2}-a^{2}}}m+{\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}=0.$$

Теперь, как и в случае с параболой, необходимо решить квадратное уравнение и два решения m ₁ , m ₂ подставить в уравнение $$\tan ^{2}\alpha =\left({\frac {m_{1}-m_{2}}{1+m_{1}m_{2}}}\right)^{2}.$$

Перестановка показывает, что изоптики являются частями кривой 4-й степени: $$\left(x_{0}^{2}+y_{0}^{2}-a^{2}-b^{2}\right)^{2}\tan ^{2}\alpha =4\left(a^{2}y_{0}^{2}+b^{2}x_{0}^{2}-a^{2}b^{2}\right).$$

Гипербола:

Решение для случая гиперболы можно взять из случая эллипса, заменив b ² с − б ² (как и в случае с ортопедией, см. выше ).

Чтобы визуализировать изоптику, см. неявную кривую .

Внешние ссылки

• Специальные плоские кривые.
• Математический мир
• Кривые Яна Вассенаара
• «Изоптическая кривая» в MathCurve
• «Ортоптическая кривая» в MathCurve

Ссылки

• Лоуренс, Дж. Деннис (1972). Каталог специальных плоских кривых . Дуврские публикации. стр. 58–59 . ISBN  0-486-60288-5 .
• Оденал, Борис (2010). «Эквиоптические кривые конических сечений» (PDF) . Журнал геометрии и графики . 14 (1): 29–43.
• Шааль, Герман (1977). Линейная алгебра и аналитическая геометрия . Том III. Посмотретьег. п. 220. ИСБН  3-528-03058-5 .
• Штайнер, Джейкоб (1867). Лекции по синтетической геометрии . Лейпциг: Б.Г. Тойбнер. Часть 2, с. 186.
• Тернулло, Маурицио (2009). «Два новых набора конциклических точек, связанных с эллипсом». Журнал геометрии . 94 (1–2): 159–173. дои : 10.1007/s00022-009-0005-7 . S2CID   120011519 .