✖


Jump to content

Кристаллическое двойникование

(Перенаправлено с Двойного кристалла )
Кварц – японский близнец
Схема двойниковых кристаллов альбита . На более совершенном спайности, параллельном базальной плоскости (П), расположена система тонких исчерченностей, параллельных второму спайности (М).

Двойникование кристаллов происходит, когда два или более соседних кристаллов одного и того же минерала ориентированы так, что они кристаллической решетки симметрично имеют одни и те же точки . В результате происходит срастание двух отдельных кристаллов, прочно связанных друг с другом. Поверхность, вдоль которой точки решетки являются общими в двойниковых кристаллах, называется композиционной поверхностью или двойниковой плоскостью.

Кристаллографы классифицируют двойниковые кристаллы по ряду законов двойников, специфичных для кристаллической структуры. Тип двойников может быть диагностическим инструментом при идентификации минералов. Существует три основных типа близнецов. Первый — ростовое двойникование , которое может происходить как в очень крупных, так и в очень мелких частицах. Второй — трансформационное двойникование , при котором происходит изменение кристаллической структуры. Третий — деформационное двойникование , при котором двойникование развивается в кристалле в ответ на сдвиговое напряжение и является важным механизмом постоянных изменений формы кристалла.

Определение

[ редактировать ]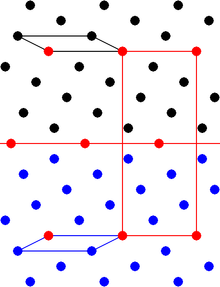
Двойная решетка (2D). Длинная горизонтальная красная линия — это композиционная плоскость, где соединяются два кристаллических сегмента. Верхняя кристаллическая решетка является отражением нижней кристаллической решетки. Красные точки — это общие точки кристаллической решетки.

Двойникование — это форма симметричного срастания двух или более соседних кристаллов одного и того же минерала. Он отличается от обычного случайного срастания минеральных зерен в минеральном отложении, поскольку относительная ориентация двух кристаллических сегментов демонстрирует фиксированную взаимосвязь, характерную для минеральной структуры. Отношения определяются операцией симметрии, называемой операцией-близнецом . [ 1 ] [ 2 ]

Операция двойника не является одной из нормальных операций симметрии несдвойниковой кристаллической структуры. Например, операция двойника может представлять собой отражение от плоскости, которая не является плоскостью симметрии монокристалла. [ 1 ] [ 2 ]

На микроскопическом уровне граница двойника характеризуется набором атомных позиций в кристаллической решетке, которые являются общими для двух ориентаций. [ 1 ] [ 2 ] Эти общие точки решетки придают соединению между сегментами кристалла гораздо большую прочность, чем соединение между случайно ориентированными зернами, так что двойниковые кристаллы нелегко расколоться. [ 3 ]

Параллельный рост описывает форму роста кристаллов, которая создает вид скопления выровненных кристаллов, которые можно принять за близнецов. При внимательном рассмотрении выяснилось, что кластер на самом деле представляет собой монокристалл. Это не двойникование, поскольку кристаллическая решетка непрерывна по всему кластеру. Вероятно, имеет место параллельный рост, поскольку он снижает энергию системы. [ 4 ]

Двойные законы

[ редактировать ]

Законы двойников — это операции симметрии, которые определяют ориентацию между сегментами двойникового кристалла. Они так же характерны для минерала, как и углы граней его кристаллов. Например, кристаллы ставролита демонстрируют двойникование под углами почти точно 90 или 30 градусов. [ 3 ] Закон близнецов не является операцией симметрии полного набора базисных точек. [ 2 ]

Законы двойников включают операции отражения, операции вращения и операцию инверсии. Отражательное двойникование описывается индексами Миллера плоскости двойника (т.е. {hkl}), тогда как вращательное двойникование описывается направлением оси двойника (т.е. <hkl>). Инверсионное двойникование обычно эквивалентно симметрии отражения или вращения. [ 1 ]

Законы вращательного близнеца почти всегда представляют собой 2-кратное вращение, хотя возможна любая другая разрешенная симметрия вращения (3-кратная, 4-кратная, 5-кратная или 6-кратная). Ось двойника будет перпендикулярна плоскости решетки. [ 5 ] Закон вращательного двойника может иметь ту же ось, что и вращательная симметрия отдельного кристалла, если закон двойника представляет собой 2-кратное вращение, а операция симметрии представляет собой 3-кратное вращение. Это относится к закону двойникования шпинели на <111>: структура шпинели имеет 3-кратную вращательную симметрию на <111>, а шпинель обычно двойникуется за счет 2-кратного вращения на <111>. [ 1 ]

Граница между сегментами кристалла называется поверхностью состава или, если она плоская, плоскостью состава . Плоскость композиции часто, хотя и не всегда, параллельна плоскости закона двойников закона отражения. В этом случае плоскость двойника всегда параллельна возможной грани кристалла. [ 2 ]

Общие законы близнецов

[ редактировать ]
Шпинелевой закон контактного двойникования. Слева показан монокристалл, плоскость состава выделена красным. Справа: кристалл фактически разрезан по композиционной плоскости, а передняя половина повернута на 180°, чтобы образовался контактный двойник. Это создает повторные входы вверху, внизу слева и внизу справа от плоскости композиции. [ 3 ]

В изометрической системе наиболее распространенными типами двойников являются Закон Шпинели (двойная плоскость, параллельная октаэдру ) <111>, где ось двойника перпендикулярна грани октаэдра, и Железный крест <001>, который является взаимопроникновение двух пиритоэдров, подтип додекаэдра . [ 6 ]

В гексагональной системе кальцит демонстрирует законы контактных двойников {0001} и {0112}. Кварц демонстрирует Закон Бразилии {1120} и Закон Дофине <0001>, которые являются двойниками проникновения, вызванными трансформацией, и Закон Японии {1122}, который часто возникает в результате случайностей во время роста. [ 6 ]

В тетрагональной системе наиболее часто наблюдаемым типом двойников являются циклические контактные двойники, например, в рутила диоксиде титана и оксиде олова касситерита . [ 6 ]

В орторомбической системе кристаллы обычно двойниковаются в плоскостях, параллельных грани призмы, где наиболее распространенным является двойник {110}, который образует циклические двойники, такие как арагонит , хризоберилл и церуссит . [ 6 ]

В моноклинной системе двойники чаще всего встречаются на плоскостях {100} и {001} по закону Манебаха {001}, закону Карлсбада [001], закону Бавено {021} в ортоклазе и двойникам ласточкиного хвоста (закону Манебаха). {001} в гипсе . [ 6 ]

В триклинной системе наиболее часто двойниковыми кристаллами являются полевого шпата минералы плагиоклаз и микроклин . Эти минералы демонстрируют законы альбита и периклина. [ 5 ] [ 6 ]

наиболее распространенные двойные операции в кристаллической системе Ниже приведены . Этот список не является исчерпывающим, особенно для кристаллических систем самой низкой симметрии, таких как триклинная система. [ 7 ] [ 1 ] [ 6 ]

30° двойник ставролита
90° двойники ставролита
Крест-двойник из железного пирита
Система Закон Операция Примеры
Триклиника Альбитовый закон
Периклинальный закон
Карловарский закон
Закон Бавено
Закон Манебаха 		{010}
<010>
<001>
{021}
{001} 		Плагиоклаз
Моноклиника Карловарский закон
Закон Бавено
Закон Манебаха 		<001>
{021}
{001}
{100}
<031>
<231> 		Ортоклаз

Гипс

Ставролит
орторомбический {110}
{101}
{011} 		Арагонит, церрусит; часто циклический
четырехугольный {110}
{101}
{011} 		Касситерит, рутил
Шестиугольный


Закон Бразилии
Закон Дофина
Законодательство Японии 		{01 1 2}
{0001}
{10 1 1}
{11 2 0}
<0001>
{11 2 2} 		Кальцит


Кварц
Изометрический Шпинелевой закон


Закон железного креста 		<111>
{111}
{001}
<001> 		Шпинель


Пирит

Виды побратимства

[ редактировать ]
Хризоберилл с циклическим двойникованием

Простые двойниковые кристаллы могут быть контактными двойниками или двойниками проникновения. Контактные близнецы встречаются в одной композиционной плоскости, часто появляясь через границу как зеркальные изображения. Плагиоклаз , кварц , гипс и шпинель часто обнаруживают контактное двойникование. [ 3 ] Мероэдрическое двойникование возникает, когда решетки контактных двойников накладываются в трех измерениях, например, путем относительного вращения одного двойника относительно другого. [ 8 ] Примером является метацеунерит . [ 9 ] Контактное двойникование обычно создает входящие грани, где грани сегментов кристалла встречаются на плоскости контакта под углом более 180 °. [ 3 ]

Тип двойников, включающий отношения на 180°, называется гемитропизмом или гемитропией .

В двойниках проникновения отдельные кристаллы выглядят проходящими друг через друга. симметрично [ 3 ] Ортоклаз , ставролит , пирит и флюорит часто обнаруживают проникающее двойникование. Поверхность композиции в двойниках проникновения обычно неровная и простирается к центру кристалла. [ 2 ]

Контактное двойникование может возникнуть в результате отражения или вращения, тогда как проникающее двойникование обычно возникает в результате вращения. [ 2 ]

Если несколько частей двойникового кристалла выровнены по одному и тому же закону двойников, их называют множественными или повторяющимися двойниками . Если эти несколько близнецов расположены параллельно, их называют полисинтетическими близнецами . Когда множественные близнецы не параллельны, они являются циклическими близнецами . Альбит , кальцит и пирит часто демонстрируют полисинтетическое двойникование. Близко расположенные полисинтетические двойники часто наблюдаются в виде полос или тонких параллельных линий на грани кристалла. Циклические двойники возникают в результате повторения двойников вокруг оси вращения. Этот тип двойников происходит вокруг трех, четырех, пяти, шести или восьмикратных осей. Соответствующие модели называются тройками, четверками, пятерками , шестерками и восьмерками. Шестёрки распространены в арагоните. [ 10 ] [ 11 ] Рутил , арагонит , церуссит и хризоберилл часто демонстрируют циклическое двойникование, обычно радиационное. [ 3 ] [ 2 ]

При ротационном двойниковании соотношение между осью двойника и плоскостью двойника делится на один из трех типов: [ 12 ]

  1. параллельное двойникование, когда ось двойника и композиционная плоскость лежат параллельно друг другу,
  2. нормальное двойникование, когда двойниковая плоскость и композиционная плоскость лежат нормально, и
  3. сложное двойникование — сочетание параллельного и нормального двойникования в одной композиционной плоскости.

Способы формирования

[ редактировать ]
Параллельный рост пироморфита

Существует три способа образования двойниковых кристаллов.

  • Ростовые двойники являются результатом прерывания или изменения решетки во время формирования или роста. Это может быть связано с более крупным замещающим ионом, статистикой, поскольку разница в энергии для зарождения новой плоскости атомов в двойниковой ориентации мала, или потому, что двойники приводят к структуре с более низкой энергией.
  • отжига или Двойники трансформации являются результатом изменения кристаллической системы во время охлаждения, поскольку одна форма становится нестабильной, и кристаллическая структура должна реорганизоваться или трансформироваться в другую, более стабильную форму.
  • Деформация или скольжение двойников являются результатом напряжения на кристалле после его формирования. Поскольку двойники роста образуются во время первоначального роста кристалла, они описываются как первичные , тогда как двойники трансформации или деформации образуются в существующем кристалле и описываются как вторичные . [ 13 ]

Ростовое двойникование (нанотвиннинг)

[ редактировать ]
Пятикратный двойник в наночастице золота ( микрофотография электронного микроскопа ).

Существует два типа двойникования, которые могут возникнуть во время роста: случайное и такое, при котором двойниковая структура имеет более низкую энергию.

При случайном росте двойникования атом присоединяется к грани кристалла в положении, далеком от идеального, образуя зародыш для роста двойника. Исходный кристалл и его двойник затем срастаются и становятся очень похожими друг на друга. Это достаточно характерно для некоторых минералов, чтобы предположить, что они термодинамически или кинетически предпочтительнее в условиях быстрого роста. [ 3 ] [ 1 ]

От них отличаются близнецы, обнаруженные в наночастицах, таких как изображение здесь, причем эти пятикратные или десятиэдрические наночастицы являются одними из наиболее распространенных. [ 14 ] Эти циклические двойники возникают, поскольку при небольших размерах они имеют меньшую энергию. [ 15 ] Для показанного пятикратного случая имеется дисклинация вдоль общей оси. [ 16 ] что приводит к дополнительной энергии деформации. [ 17 ] Уравновешивает это уменьшение поверхностной свободной энергии, в значительной степени из-за большего количества (111) граней поверхности. [ 18 ] В небольших наночастицах декаэдрическая и более сложная икосаэдрическая структура (с двадцатью единицами) имеют более низкую энергию, но при более высоких энергиях монокристаллы становятся более низкой энергией. [ 19 ] [ 20 ] Однако им не обязательно превращаться в монокристаллы, они могут вырасти очень большими и известны как пятёрки, что было задокументировано ещё в 1831 году Густавом Роузом ; [ 21 ] дальнейшие рисунки доступны в Atlas der Kristallformen, а также см. статью о пятёрках . [ 22 ]

Трансформационное побратимство

[ редактировать ]
Иллюстрация преобразования двойников в 2D. Орторомбический кристалл слева превращается в моноклинный кристалл справа с двумя параллельными плоскостями двойникования (полисинтетическое двойникование).

Двойникование при трансформации и отжиге происходит, когда в охлаждающемся кристалле происходит смещающий полиморфный переход. Например, лейцит имеет изометрическую кристаллическую структуру при температуре выше 665 ° C (1229 ° F), но ниже этой температуры становится тетрагональной. Любая из трех исходных осей кристалла может стать длинной осью, когда происходит этот фазовый переход. Двойникование возникает, когда разные части кристалла нарушают свою изометрическую симметрию вдоль разного выбора оси. Обычно это полисинтетическое двойникование, которое позволяет кристаллу сохранять свою изометрическую форму за счет усреднения смещения в каждом направлении. В результате образуется псевдоморфный кристалл, имеющий изометрическую симметрию. Калиевый полевой шпат также испытывает полисинтетическое двойникование при переходе от моноклинной структуры ( ортоклаз ) к триклинной структуре ( микроклин ) при медленном охлаждении. [ 1 ]

Деформационное двойникование

[ редактировать ]
Анимация деформационного двойникования кристалла

Деформационное двойникование является реакцией на напряжение сдвига. Кристаллическая структура смещается вдоль последовательных плоскостей кристалла, этот процесс также называется скольжением . Двойникование всегда является двойникованием отражения, а плоскость скольжения также является зеркальной плоскостью. Деформационное двойникование можно наблюдать во фрагменте скола кальцита, слегка надавив лезвием ножа возле края. Этот конкретный скользящий двойник {102} почти повсеместно встречается в деформированных пластах горных пород, содержащих кальцит. [ 1 ]

Двойникование и скольжение являются конкурентными механизмами деформации кристаллов . Каждый механизм является доминирующим в определенных кристаллических системах и при определенных условиях. [ 23 ] В ГЦК-металлах скольжение почти всегда является доминирующим, поскольку требуемое напряжение намного меньше, чем напряжение двойникования. [ 24 ]

Двойникование может происходить за счет совместного смещения атомов вдоль поверхности границы двойника. Это смещение большого количества атомов одновременно требует значительной энергии. Следовательно, теоретическое напряжение, необходимое для образования двойника, довольно велико. Считается, что двойникование связано с движением дислокаций в согласованном масштабе, в отличие от скольжения, которое вызвано независимым скольжением в нескольких местах кристалла .

по своей природе характеру деформации По сравнению со скольжением, двойникование приводит к более неоднородному . Эта деформация создает локальный градиент по всему материалу и вблизи пересечений двойников и границ зерен. Градиент деформации может привести к разрушению по границам, особенно в ОЦК-переходных металлах при низких температурах.

Из трех распространенных кристаллических структур bcc , fcc и hcp структура hcp с наибольшей вероятностью образует двойники деформации при растяжении, поскольку они редко имеют достаточное количество систем скольжения для произвольного изменения формы. Высокие скорости деформации, низкая энергия дефектов упаковки и низкие температуры способствуют деформационному двойникованию. [ 25 ]

Если металл с гранецентрированной кубической (ГЦК) структурой, такой как Al, Cu, Ag, Au и т. д., подвергается напряжению, в нем возникает двойникование. Образование и миграция двойниковых границ частично ответственны за пластичность и ковкость ГЦК-металлов. [ 26 ]

Двойные границы отчасти ответственны за ударное упрочнение и за многие изменения, возникающие при холодной обработке металлов с системами ограниченного скольжения или при очень низких температурах. Они также происходят из-за мартенситных превращений : движение границ двойников отвечает за псевдоупругое поведение нитинола с памятью формы , а их присутствие частично отвечает за твердость из- закалки стали за . В некоторых типах высокопрочных сталей двойники очень мелкой деформации выступают в качестве основных препятствий движению дислокаций. Эти стали называются сталями «TWIP», где TWIP означает пластичность, вызванную двойникованием . [ 27 ]

Кристаллография деформационного двойникования

[ редактировать ]
Кристаллографические плоскости деформационного двойникования

Двойникование кристаллографически определяется его двойниковой плоскостью 𝑲 𝟏 , зеркальной плоскостью в двойниковом и родительском материале, и 𝜼 𝟏, которая является направлением двойникового сдвига. Двойники деформации в Zr обычно имеют линзовидную форму, удлиняются в направлении 𝜼 𝟏 и утолщаются вдоль нормали плоскости 𝑲 𝟏 . [ 28 ]

Плоскость-двойник, направление сдвига и плоскость сдвига образуют базисные векторы ортогонального набора. Отношения разориентации оси и угла между родительским объектом и близнецом представляют собой поворот угла 𝜉 вокруг нормального направления плоскости сдвига 𝑷.

В более общем смысле двойникование можно описать как поворот на 180° вокруг оси (𝑲 𝟏 для близнецов I типа или 𝜼 𝟏 для близнецов II типа, нормальное направление) или зеркального отражения в плоскости (𝑲 𝟏 или 𝜼 𝟏 нормальная плоскость). [ 29 ]

Помимо однородного сдвига, иногда требуется перетасовка атомов для реформирования правильной кристаллической структуры в двойниковой решетке. Для каждого варианта близнеца возможен обратный близнец с поменянными местами 𝑲 𝟏 и 𝑲 2 , 𝜼 𝟏 и 𝜼 2 , но в реальности один вариант может появляться чаще из-за сложностей с необходимыми перетасовками. [ 30 ]

при сдвиге действуют только две кристаллографические плоскости, которые не меняют свою форму и размер в результате сдвига. Первая 𝑲 𝟏 — это плоскость, определяющая верхнюю и нижнюю поверхности срезаемого объема. Эта плоскость содержит направление сдвига. Другая плоскость обозначена C. Направление сдвига показано стрелкой и помечено традиционным обозначением 𝜼 𝟏 . Из вышеизложенного следует, что существует три способа сдвига кристаллической решетки с сохранением ее кристаллической структуры и симметрии:

  1. Когда 𝑲 𝟏 — рациональная плоскость, а 𝜼 2 — рациональное направление, то двойник первого рода
  2. Когда 𝑲 2 — рациональная плоскость, а 𝜼 𝟏 — рациональное направление, двойник второго рода встречается редко.
  3. Когда все четыре элемента 𝑲 𝟏 , 𝑲 2 , 𝜼 𝟏 и 𝜼 2 рациональны, составной близнец

Конфигурация деформационного двойника

[ редактировать ]
Правильные плоскости двойникования в кристалле кальцита. Изображение скрещенных николей, увеличение 10× (поле зрения = 2 мм)

Зародыш деформационного близнеца формируется в металле ОЦК путем накопления дефектов упаковки, причем выбор варианта определяется локальным напряженным состоянием. [ 31 ] [ 32 ] [ 33 ] Изменение поля напряжений вблизи двойников, полученное на основе HR- EBSD эксперимента [ 34 ] [ 35 ] Данные моделирования методом конечных элементов кристаллической пластичности ( CPFE ) показали, что двойники зарождаются в местах с максимальной плотностью энергии деформации и разрешаемым двойником сдвиговым напряжением ; таким образом, уменьшая общую упругую энергию после формирования. Эта релаксация зависит от толщины двойника и является решающим фактором при определении расстояния между двойниками. [ 36 ] Экспериментальный [ 37 ] и трехмерный [ 38 ] анализ был сосредоточен на (сохраненной) плотности энергии деформации, измеренной вдоль траектории. Это высоко локализованное поле напряжений может обеспечить достаточную движущую силу для одновременного зарождения двойников. [ 39 ] и зарождение меж/внутризеренных трещин .

Рост деформационного двойника можно воспринимать как двухэтапный процесс: i) утолщение, которое опосредуется взаимодействием между остаточными и подвижными частями двойника на когерентном интерфейсе близнец-родитель; [ 40 ] и ii) подвижность дислокаций вдоль направления двойного сдвига. [ 41 ] Двойник распространяется, когда однородное напряжение сдвига достигает критического значения, и двойник-родительский интерфейс продвигается внутрь родительского зерна [240]. Распространяющийся деформационный двойник создает поле напряжений из-за его удержания окружающим родительским кристаллом, а деформационные двойники приобретают форму трехмерного сплюснутого сфероида (который проявляется в двумерных сечениях как двояковыпуклая линза ) со смешанным когерентным и некогерентным интерфейсом ( Рисунок б). [ 41 ]

Каннан и др. [ 42 ] с помощью сверхвысокоскоростной оптической визуализации in-situ обнаружил, что зарождение двойников в монокристаллическом магнии вызвано напряжением и сопровождается мгновенным распространением со скоростью 1 км / с (первоначально), что отдает предпочтение объемному латеральному утолщению над прямым распространением, минуя критическую ширину, при которой рост становится быстрее в направлении сдвига. Барнетт [ 43 ] также указано, что рост происходит за счет удлинения двойного кончика. Кроме того, упругое моделирование локального поля напряжений , окружающего эллипсоидный кончик двойника, показывает, что это поле можно описать с помощью угла линзы ( ) и что величина поля напряжений увеличивается с толщиной двойника. [ 44 ]

(a) Изображение диода прогнозирующего рассеяния электронов (FSD) для двойников деформации на границе зерен в стареющем феррите на I) рабочем расстоянии 18 мм и II) рабочем расстоянии 38 мм. (б) Схема двояковыпуклого двойника с межфазными дислокациями и (в) Двойная полоса. [ 45 ]

На практике пластическая аккомодация происходит в родительском кристалле ; таким образом, он также зависит от предела текучести материала, анизотропной упругой жесткости исходной кристаллической решетки и величины сдвига деформационного двойникования. [ 40 ] Это также может сопровождаться дальнодействующей диффузией элементов и сегрегацией элементов (например, Cr и Co в монокристаллическом суперсплаве MD2 на основе Ni ), которая происходит на границе двойников, чтобы облегчить рост двойников за счет снижения критической энергии дефекта упаковки. [ 46 ] Наблюдалось линейное изменение между толщиной двойника, энергией дефекта упаковки и размером зерна. [ 47 ] и в меньшей степени – напряженное состояние двойникового зерна ( Фактор Шмида ). [ 48 ] Толщина двойника насыщается, когда критическая плотность остаточных дислокаций достигает когерентной границы родительского кристалла двойника. [ 33 ] [ 49 ]

Значительное внимание уделялось кристаллографии . [ 50 ] морфология [ 51 ] и макромеханические эффекты [ 52 ] деформационного двойникования. Хотя критерий роста деформационного двойника не совсем понятен, это контролируемое явление, связанное с взаимодействием между остаточными и подвижными частями двойника на границе раздела двойников; термодинамически сюда входят упругая энергия напряженной решетки, граница раздела и объемная свободная энергия двойника, а также диссипированная энергия механизма роста. [ 53 ] Чтобы полностью понять взаимодействие между микроструктурой (т.е. размером зерна, текстурой), температурой и скоростью деформации при деформационном двойниковании, крайне важно охарактеризовать (высокое) локальное поле напряжений и деформаций, связанное с утолщением и распространением двойников. Это особенно важно для материалов, в которых разрушение спайности может быть инициировано двойникованием (например, железо-кремний, ферритная фаза стареющей дуплексной нержавеющей стали и монокристаллический магний ) в качестве механизма снятия напряжений.

Ранние исследования деформационных двойников, задержанных внутри зерен ниобия [ 54 ] и железо [ 55 ] визуализировали высокую локальную концентрацию деформации на двойном кончике, используя процедуру травления. Совсем недавно дифракция обратного рассеяния электронов высокого разрешения (HR- EBSD ) была использована для исследования «сингулярности» деформации перед кончиком двойника в гексагональном циркониевом сплаве с плотной упаковкой (HCP). Деформационный двойник из титана технической чистоты был охарактеризован аналогичным образом, а затем количественно оценен с использованием локального фактора Шмида (LSF) на кончике двойника. [ 56 ] как описано в уравнении ниже.

где σ — тензор напряжений, S я – тензор Шмида, P я – его симметричная часть, d я — направление сдвига, а n я – плоскость сдвига, нормальная для i-й системы скольжения . Авторы пришли к выводу, что условия в вершине двойника контролируют утолщение и распространение аналогично работе источников дислокаций перед вершиной трещины. [ 57 ] В анализе широкая область с высоким LSF перед кончиком двойника способствовала распространению, тогда как узкая область с высоким LSF способствовала утолщению. С тех пор утверждалось [ 58 ] что LSF жестко контролирует выбор вариантов близнецов, поскольку двойникование имеет сильную полярность.

Новинка LSF – по сравнению с другими критериями для описания условий в близнеце [ 47 ] – заключается в объединении геометрического критерия с полем деформации в исходном зерне для обеспечения приблизительного указания локальной двойниковой моды (т. е. утолщения или распространения). Однако анализ LSF не использует имеющиеся данные всего поля, опирается на глобальную информацию о приложенном напряжении и не учитывает энергетический баланс, который стимулирует рост близнецов. Было проведено несколько экспериментов на месте для количественной оценки поля деформаций перед распространяющимся двойником деформации. [ 45 ] [ 35 ] Такие наблюдения могут подтвердить геометрические или гибридные критерии, основанные на геометрической энергии. [ 58 ] для роста. Наномасштабные испытания (т.е. просвечивающая электронная микроскопия ) могут не отражать поведение объемных образцов из-за отсутствия пластичности, т.е. большого отношения площади поверхности к объему, [ 59 ] поэтому необходим подходящий метод анализа.

Ллойд [ 49 ] описал поле концентрации напряжений перед кончиком двойника, используя двумерную модель дислокаций внутри одного зерна магния . Ван и Ли, [ 60 ] рассматривавший микроскопические фазовые (МФП) модели трещин, отметил, что поля напряжений схожи для дислокаций , деформационного двойникования и мартенситных превращений, с различиями только в тяге создаваемой поверхности, т.е. для дислокаций наблюдается 100% восстановление тяги. и поверхность без сцепления для трещины. поля напряжений Они подчеркнули, что сингулярность регулирует продвижение вершины трещины и дислокаций . Эту концентрацию напряжений можно охарактеризовать с помощью линейного интеграла, не зависящего от пути , как показано Эшелби для дислокаций , учитывая вклад поверхностного натяжения и эллипсоидальных включений : [ 61 ] и рис [ 62 ] для трещин и концентраций напряжений на поверхностях без сцепления. Кроме того, Венейблс [ 63 ] отметил, что сплюснутая сфероидная форма двойного кончика является идеальным примером эллипсоидного включения или выемки.

См. также

[ редактировать ]
Викискладе есть медиафайлы по теме двойниковых кристаллов .

Ссылки

[ редактировать ]
  1. ^ Перейти обратно: а б с д и ж г час я Нессе, Уильям Д. (2000). Введение в минералогию . Нью-Йорк: Издательство Оксфордского университета. стр. 87–91. ISBN  9780195106916 .
  2. ^ Перейти обратно: а б с д и ж г час Кляйн, Корнелис; Херлбат, Корнелиус С. младший (1993). Руководство по минералогии: (по Джеймсу Д. Дане) (21-е изд.). Нью-Йорк: Уайли. стр. 102–106. ISBN  047157452X .
  3. ^ Перейти обратно: а б с д и ж г час Синканкас, Джон (1964). Минералогия для любителей . Принстон, Нью-Джерси: Ван Ностранд. стр. 96–105. ISBN  0442276249 .
  4. ^ Кляйн и Херлбат 1993 , с. 101.
  5. ^ Перейти обратно: а б Нельсон, Стивен А. (2013). «Двойникование, полиморфизм, политипизм, псевдоморфизм» . Тулейнский университет . Проверено 19 февраля 2022 г.
  6. ^ Перейти обратно: а б с д и ж г Кляйн и Херлбат 1993 , стр. 104–106.
  7. ^ Нессе 2000 , стр. 89, 214–216.
  8. ^ Йейтс, Тодд О. (1997). «[22] Обнаружение и преодоление двойников кристаллов». Макромолекулярная кристаллография . Часть А. Методы энзимологии. Том. 276. стр. 344–358. дои : 10.1016/S0076-6879(97)76068-3 . ISBN  9780121821777 . ПМИД   27799105 .
  9. ^ Локок, Эй Джей; Бернс, ПК (1 апреля 2003 г.). «Кристаллические структуры и синтез медно-доминантных членов групп аутюнита и метааутюнита: торбернита, цейнерита, метаторбернита и метацеунита». Канадский минералог . 41 (2): 489–502. Бибкод : 2003CaMin..41..489L . дои : 10.2113/gscanmin.41.2.489 .
  10. ^ Дьяр и Гюнтер 2008 , стр. 41–43
  11. ^ Честерман и Лоу 2008 , с. 39
  12. ^ Тоби, Александр К. (1961). «Распознавание двойников плагиоклаза в сечениях, нормальных к плоскости состава» . Американский минералог . 46 (11–12): 1470–1488 . Проверено 19 февраля 2022 г.
  13. ^ Кляйн и Херлбат 1993 , с. 167.
  14. ^ Хофмайстер, Х. (1998). <3::aid-crat3>3.0.co;2-3 «Сорок лет исследования пятикратных двойниковых структур в малых частицах и тонких пленках» . Кристаллические исследования и технологии . 33 (1): 3–25. Бибкод : 1998CryRT..33....3H . doi : 10.1002/(sici)1521-4079(1998)33:1<3::aid-crat3>3.0.co;2-3 . ISSN   0232-1300 .
  15. ^ Маркс, Лоуренс. Д. (2023), «Форма, термодинамика и кинетика наночастиц» , Энциклопедия наноматериалов , Elsevier, стр. 383–417, doi : 10.1016/b978-0-12-822425-0.00082-8 , ISBN  978-0-12-822423-6 , получено 11 июля 2023 г.
  16. ^ Вит, Р де (1972). «Частичные дисклинации» . Журнал физики C: Физика твердого тела . 5 (5): 529–534. Бибкод : 1972JPhC....5..529D . дои : 10.1088/0022-3719/5/5/004 . ISSN   0022-3719 .
  17. ^ Хауи, А.; Маркс, Л.Д. (1984). «Упругие деформации и энергетический баланс для многократно сдвойникованных частиц» . Философский журнал А. 49 (1): 95–109. Бибкод : 1984PMagA..49...95H . дои : 10.1080/01418618408233432 . ISSN   0141-8610 .
  18. ^ Маркс, Л.Д. (1984). «Структура поверхности и энергетика многократно сдвойникованных частиц» . Философский журнал А. 49 (1): 81–93. Бибкод : 1984PMagA..49...81M . дои : 10.1080/01418618408233431 . ISSN   0141-8610 .
  19. ^ Балетто, Франческа; Феррандо, Риккардо (2005). «Структурные свойства нанокластеров: энергетические, термодинамические и кинетические эффекты» . Обзоры современной физики . 77 (1): 371–423. Бибкод : 2005РвМП...77..371Б . дои : 10.1103/RevModPhys.77.371 . ISSN   0034-6861 .
  20. ^ Роджерс, Блейк; Лер, Александр; Веласкес-Салазар, Х. Хесус; Уеттен, Роберт; Мендоса-Круз, Рубен; Базан-Диас, Лурд; Бахена-Урибе, Даниэль; Хосе Якаман, Мигель (2023). «Декаэдры и икосаэдры повсюду: аномальная кристаллизация золота и других металлов на наномасштабе» . Кристаллические исследования и технологии . 58 (4). Бибкод : 2023CryRT..5800259R . дои : 10.1002/crat.202200259 . ISSN   0232-1300 .
  21. ^ Роза, Густав (1831). «О кристаллических формах золота и серебра» . Анналы физики . 99 (10): 196–204. Бибкод : 1831АнП....99..196Р . дои : 10.1002/andp.18310991003 . ISSN   0003-3804 .
  22. ^ Гольдшмидт, В. (1918). Атлас кристаллических форм, V4, пластины . Книжный магазин Университета Карла Уинтерса. стр. Табличка 48, рис. 21. (Золото). hdl : 2027/nyp.33433084029887 .
  23. ^ Махаджан, С.; Уильямс, Д.Ф. (июнь 1973 г.). «Деформационное двойникование металлов и сплавов». Международные металлургические обзоры . 18 (2): 43–61. дои : 10.1179/imtlr.1973.18.2.43 .
  24. ^ Байерляйн, Ирен Дж.; Мара, Натан А.; Бхаттачарья, Дхрити; Александр, Дэвид Дж.; Некер, Карл Т. (январь 2011 г.). «Эволюция текстуры посредством комбинированного скольжения и деформационного двойникования в прокатанном эвтектическом нанокомпозите, отлитом из серебра и меди». Международный журнал пластичности . 27 (1): 121–146. дои : 10.1016/j.ijplas.2010.05.007 .
  25. ^ Кортни, Томас Х. (2000) Механическое поведение материалов , 2-е изд. МакГроу Хилл. ISBN   1-57766-425-6
  26. ^ Нурул Акмаль Че, Ла; Тригерос, Соня (2019). «Синтез и моделирование механических свойств нанопроволок Ag, Au и Cu» . наук. Технол. Адв. Мэтр . 20 (1): 225–261. Бибкод : 2019STAdM..20..225L . дои : 10.1080/14686996.2019.1585145 . ПМК   6442207 . ПМИД   30956731 .
  27. ^ Штайнмец, доктор медицинских наук; Япель, Т.; Витброк, Б.; Эйзенлор, П.; Гутьеррес-Уррутия, И.; Саид (2013), «Выявление поведения пластичных сталей, вызванных двойникованием, при деформационном упрочнении: теория, моделирование, эксперименты», Acta Materialia , 61 (2): 494, Bibcode : 2013AcMat..61..494S , doi : 10.1016/ j.actamat.2012.09.064 .
  28. ^ Кристиан, JW; Махаджан, С. (1995). «Деформационное двойникование» . Прогресс в материаловедении . 39 (1–2): 1–157. дои : 10.1016/0079-6425(94)00007-7 .
  29. ^ Калхун, Калифорния; Гарлеа, Э.; Сиснерос, штат Техас; Агнью, СР (апрель 2018 г.). «Нейтронографическая характеристика температурной зависимости деформации в α-уране» . Журнал ядерных материалов . 502 : 60–67. Бибкод : 2018JNuM..502...60C . дои : 10.1016/j.jnucmat.2018.01.036 . ОСТИ   1478070 .
  30. ^ Билби, бакалавр; Крокер, А.Г. (26 октября 1965 г.). «Теория кристаллографии деформационного двойникования» . Труды Лондонского королевского общества. Серия А. Математические и физические науки . 288 (1413): 240–255. Бибкод : 1965RSPSA.288..240B . дои : 10.1098/rspa.1965.0216 . ISSN   0080-4630 . S2CID   120566509 .
  31. ^ Кан, RW (октябрь 1954 г.). «Сдвоенные кристаллы». Достижения физики . 3 (12): 363–445. Бибкод : 1954AdPhy...3..363C . дои : 10.1080/00018735400101223 . ISSN   0001-8732 .
  32. ^ Ван, С.; Шуман, К.; Бао, Л.; Лекомт, Дж.С.; Чжан, Ю.; Раулот, Ж.М.; Филипп, MJ; Чжао, X.; Эслинг, К. (май 2012 г.). «Критерий выбора вариантов двойников в титановых сплавах, деформируемых прокаткой» (PDF) . Акта Материалия . 60 (9): 3912–3919. Бибкод : 2012AcMat..60.3912W . дои : 10.1016/j.actamat.2012.03.046 .
  33. ^ Перейти обратно: а б Кристиан, JW (2002). «Деформационное двойникование». Теория превращений металлов и сплавов . Эльзевир. стр. 859–960. дои : 10.1016/b978-008044019-4/50025-8 . ISBN  978-0-08-044019-4 .
  34. ^ Абдолванд, Хамидреза; Седагат, Омид; Го, И (октябрь 2018 г.). «Зарождение и рост двойников { 11 2 2 } в титане: поля упругой энергии и напряжений вблизи двойников». Материалия . 2 : 58–62. дои : 10.1016/j.mtla.2018.06.012 . S2CID   139852253 .
  35. ^ Перейти обратно: а б Го, Ю.; Швиджик, Дж.; Михлер, Дж.; Медер, X. (1 ноября 2016 г.). «О зарождении и росте двойника {112¯2} в титане технической чистоты: исследование in situ локального поля напряжений и распределения плотности дислокаций». Акта Материалия . 120 : 292–301. дои : 10.1016/j.actamat.2016.08.073 . ISSN   1359-6454 .
  36. ^ Паудель, ЮбРадж; Барретт, Кристофер Д.; Чопп, Марк А.; Инал, Каан; Эль Кадири, Хайсам (июль 2017 г.). «Помимо первоначального зарождения двойников в ГПУ-металлах: микромеханическая формула для определения расстояния между двойниками во время деформации» . Акта Материалия . 133 : 134–146. Бибкод : 2017AcMat.133..134P . дои : 10.1016/j.actamat.2017.05.013 . ISSN   1359-6454 .
  37. ^ Параматмуни, Чайтанья; Чжэн, Зебанг; Рейнфорт, В. Марк; Данн, Фионн PE (01 декабря 2020 г.). «Зародышеобразование двойников и выбор вариантов в сплавах Mg: комплексное моделирование кристаллической пластичности и экспериментальный подход» (PDF) . Международный журнал пластичности . 135 : 102778. doi : 10.1016/j.ijplas.2020.102778 . ISSN   0749-6419 . S2CID   224887964 .
  38. ^ Параматмуни, Чайтанья; Го, И; Уизерс, Филип Дж.; Данн, Фионн PE (01 августа 2021 г.). «Трехмерное механистическое исследование факторов зарождения классических двойников и выбора вариантов в магниевых сплавах: мезомасштабное моделирование и экспериментальное исследование». Международный журнал пластичности . 143 : 103027. doi : 10.1016/j.ijplas.2021.103027 . hdl : 10044/1/90290 . ISSN   0749-6419 . S2CID   236612852 .
  39. ^ Арул Кумар, М.; Байерлейн, Эй-Джей; Томе, Китай (01 сентября 2016 г.). «Влияние локальных полей напряжений на двойниковые характеристики в ГПУ-металлах» . Акта Материалия . 116 : 143–154. Бибкод : 2016AcMat.116..143A . дои : 10.1016/j.actamat.2016.06.042 . ISSN   1359-6454 .
  40. ^ Перейти обратно: а б Байерляйн, Ирен Дж.; Чжан, Синхан; Мисра, Амит (июль 2014 г.). «Двойники роста и двойники деформации в металлах» . Ежегодный обзор исследований материалов . 44 (1): 329–363. Бибкод : 2014AnRMS..44..329B . doi : 10.1146/annurev-matsci-070813-113304 . ISSN   1531-7331 .
  41. ^ Перейти обратно: а б Бриттон, ТБ; Данн, FPE; Уилкинсон, Эй Джей (8 июня 2015 г.). «О механистических основах микромасштабной деформации в гексагональных плотноупакованных металлах» . Труды Королевского общества A: Математические, физические и технические науки . 471 (2178): 20140881. Бибкод : 2015RSPSA.47140881B . дои : 10.1098/rspa.2014.0881 . S2CID   138085929 .
  42. ^ Лю, Ю.; Тан, ПЗ; Гонг, МОЙ; Маккейб, Р.Дж.; Ван, Дж.; Томе, Китай (25 июля 2019 г.). «Трёхмерный характер двойника деформации в магнии» . Природные коммуникации . 10 (1): 3308. Бибкод : 2019NatCo..10.3308L . дои : 10.1038/s41467-019-10573-7 . ISSN   2041-1723 . ПМК   6658514 . ПМИД   31346160 .
  43. ^ Барнетт, MR (25 августа 2007 г.). «Двойникование и пластичность магниевых сплавов: Часть I: «Двойниковые» двойники». Материаловедение и инженерия: А. 464 (1): 1–7. дои : 10.1016/j.msea.2006.12.037 . ISSN   0921-5093 .
  44. ^ Арул Кумар, М.; Канджарла, АК; Низгода, СР; Лебенсон, РА; Том, Китай (01 февраля 2015 г.). «Численное исследование напряженного состояния двойника деформации в магнии» . Акта Материалия 84 : 349–358. дои : 10.1016/j.actamat.2014.10.048 . ISSN   1359-6454 .
  45. ^ Перейти обратно: а б Коко, Абдалраман; Эльмукашфи, Эльсиддиг; Драгневский, Калин; Уилкинсон, Ангус Дж.; Марроу, Томас Джеймс (01 октября 2021 г.). «J-интегральный анализ полей упругих деформаций ферритовых деформационных двойников методом дифракции обратного рассеяния электронов» . Акта Материалия . 218 : 117203. Бибкод : 2021AcMat.21817203K . дои : 10.1016/j.actamat.2021.117203 . ISSN   1359-6454 .
  46. ^ Барба, Д.; Алаборт, Э.; Педраццини, С.; Коллинз, DM; Уилкинсон, Эй Джей; Багот, Пенсильвания; Муди, член парламента; Аткинсон, К.; Иерусалим, А.; Рид, RC (15 августа 2017 г.). «О механизме микродвойникования в монокристаллическом суперсплаве» . Акта Материалия . 135 : 314–329. Бибкод : 2017AcMat.135..314B . дои : 10.1016/j.actamat.2017.05.072 . hdl : 10044/1/63276 . ISSN   1359-6454 . S2CID   55924981 .
  47. ^ Перейти обратно: а б Махаджан, С.; Уильямс, Д.Ф. (1 июня 1973 г.). «Деформационное двойникование металлов и сплавов». Международные металлургические обзоры . 18 (2): 43–61. дои : 10.1179/imtlr.1973.18.2.43 . ISSN   0367-9020 .
  48. ^ Байерлейн, Эй-Джей; Каполунго, Л.; Маршалл, ЧП; Маккейб, Р.Дж.; Томе, Китай (28 мая 2010 г.). «Статистический анализ деформационного двойникования в магнии». Философский журнал . 90 (16): 2161–2190. Бибкод : 2010PMag...90.2161B . дои : 10.1080/14786431003630835 . ISSN   1478-6435 . S2CID   136111937 .
  49. ^ Перейти обратно: а б Ллойд, Джей Ти (28 февраля 2018 г.). «Дислокационная модель роста двойников внутри и между зернами» . Труды Королевского общества A: Математические, физические и технические науки . 474 (2210): 20170709. Бибкод : 2018RSPSA.47470709L . дои : 10.1098/rspa.2017.0709 . ПМЦ   5832837 . ПМИД   29507516 .
  50. ^ Венейблс, Дж. А. (1 марта 1961 г.). «Деформационное двойникование в гранецентрированных кубических металлах». Философский журнал . 6 (63): 379–396. Бибкод : 1961PMag....6..379V . дои : 10.1080/14786436108235892 . ISSN   0031-8086 .
  51. ^ Йоханссон, Йохан; Оден, Магнус (1 июня 2000 г.). «Распределение нагрузки между аустенитом и ферритом в дуплексной нержавеющей стали при циклическом нагружении». Металлургические и сырьевые операции А . 31 (6): 1557–1570. дои : 10.1007/s11661-000-0166-3 . ISSN   1543-1940 . S2CID   137142133 .
  52. ^ Марроу, Ти Джей; Кинг, Дж. Э. (15 июня 1994 г.). «Механизмы распространения усталостных трещин в термически состаренной дуплексной нержавеющей стали». Материаловедение и инженерия: А. 183 (1): 91–101. дои : 10.1016/0921-5093(94)90893-1 . ISSN   0921-5093 .
  53. ^ Кристиан, JW; Махаджан, С. (1 января 1995 г.). «Деформационное двойникование». Прогресс в материаловедении . 39 (1): 1–157. дои : 10.1016/0079-6425(94)00007-7 . ISSN   0079-6425 .
  54. ^ Слисвик, А.В. (1 августа 1962 г.). «Эмиссарные дислокации: теория и эксперименты по распространению двойников деформации в α-железе». Акта Металлургика . 10 (8): 705–725. дои : 10.1016/0001-6160(62)90040-8 . ISSN   0001-6160 .
  55. ^ Спредборо, Дж.; Лангейнрих, Д.; Андерсон, Э.; Брэндон, Д. (декабрь 1964 г.). «Наблюдения в ямах травления относительно двойников в железе и железных сплавах». Журнал прикладной физики . 35 (12): 3585–3587. Бибкод : 1964JAP....35.3585S . дои : 10.1063/1.1713275 . ISSN   0021-8979 .
  56. ^ Го, Ю.; Абдолванд, Х.; Бриттон, ТБ; Уилкинсон, Эй Джей (01 марта 2017 г.). «Рост двойников {11 2 2} в титане: комбинированное экспериментальное и модельное исследование локального состояния деформации» . Акта Материалия . 126 : 221–235. дои : 10.1016/j.actamat.2016.12.066 . hdl : 10044/1/67478 . ISSN   1359-6454 . S2CID   136128910 .
  57. ^ Баксеванакис, КП; Гургиотис, Пенсильвания; Георгиадис, Х.Г. (июль 2017 г.). «Взаимодействие трещин с дислокациями в парной упругости. Часть I. Режим раскрытия» . Международный журнал твердых тел и структур . 118–119: 179–191. doi : 10.1016/j.ijsolstr.2017.03.019 . ISSN   0020-7683 . S2CID   55155535 .
  58. ^ Перейти обратно: а б Качер, Джош; Сабиш, Джулиан Э.; Минор, Эндрю М. (01 июля 2019 г.). «Статистический анализ взаимодействия двойников и границ зерен в чистом рении» . Акта Материалия . 173 : 44–51. Бибкод : 2019AcMat.173...44K . дои : 10.1016/j.actamat.2019.04.051 . ISSN   1359-6454 .
  59. ^ Гонг, Мингю; Хирт, Джон П.; Лю, Юэ; Шен, Яо; Ван, Цзянь (3 ноября 2017 г.). «Интерфейсные структуры и механизмы двойникования двойников в гексагональных металлах» . Письма об исследованиях материалов . 5 (7): 449–464. дои : 10.1080/21663831.2017.1336496 . S2CID   136448819 .
  60. ^ Ван, Юньчжи; Ли, Цзюй (01 февраля 2010 г.). «Фазовое поле моделирования дефектов и деформаций». Акта Материалия . 58 (4): 1212–1235. Бибкод : 2010AcMat..58.1212W . дои : 10.1016/j.actamat.2009.10.041 . ISSN   1359-6454 .
  61. ^ Эшелби, Джон Дуглас; Мотт, Невилл Фрэнсис (6 ноября 1951). «Сила, действующая на упругую особенность» . Философские труды Лондонского королевского общества. Серия А, Математические и физические науки . 244 (877): 87–112. Бибкод : 1951RSPTA.244...87E . дои : 10.1098/rsta.1951.0016 . S2CID   14703976 .
  62. ^ Райс, младший (1 июня 1968 г.). «Независимый от траектории интеграл и приближенный анализ концентрации деформации по выемкам и трещинам» . Журнал прикладной механики . 35 (2): 379–386. Бибкод : 1968JAM....35..379R . дои : 10.1115/1.3601206 . ISSN   0021-8936 .
  63. ^ Венейблс, Дж. А. (1 июля 1964 г.). «Электронная микроскопия деформационного двойникования». Журнал физики и химии твердого тела . 25 (7): 685–692. Бибкод : 1964JPCS...25..685В . дои : 10.1016/0022-3697(64)90177-5 . ISSN   0022-3697 .

Источники

[ редактировать ]
[ редактировать ]
Retrieved from "https://en.wikipedia.org/w/index.php?title=Crystal_twinning&oldid=1232636716"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: d8689b7ff278486f455021c505bea0e9__1720112160
URL1:https://arc.ask3.ru/arc/aa/d8/e9/d8689b7ff278486f455021c505bea0e9.html
Заголовок, (Title) документа по адресу, URL1:
Crystal twinning - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)