Инъективный объект

В математике , особенно в области теории категорий , понятие инъективного объекта является обобщением понятия инъективного модуля . Это понятие важно в когомологиях , в теории гомотопий и в теории модельных категорий . Двойственное понятие — это понятие проективного объекта .

Определение

Объект Q является инъективным, если для данного мономорфизма f : X → Y любой g : X → Q можно расширить до Y .

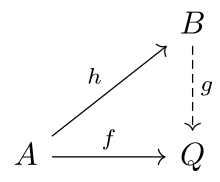
Объект ​ $Q$ в категории $\mathbf {C}$ называется инъективным, если для любого мономорфизма $f:X\to Y$ и каждый морфизм $g:X\to Q$ существует морфизм $h:Y\to Q$ расширение $g$ к $Y$, то есть такой, что $h\circ f=g$.

То есть каждый морфизм $X\to Q$ факторы через каждый мономорфизм $X\hookrightarrow Y$.

Морфизм $h$ в приведенном выше определении не обязательно должно однозначно определяться $f$ и $g$.

В локально малой категории это эквивалентно требованию, чтобы функтор hom $\operatorname {Hom} _{\mathbf {C} }(-,Q)$ несет мономорфизмы в $\mathbf {C}$ к сюръективным отображениям множеств.

В абелевых категориях

Понятие инъективности было впервые сформулировано для абелевых категорий , и это до сих пор является одной из основных областей его применения. Когда $\mathbf {C}$ категория, объект Q — абелева $\mathbf {C}$ инъективен тогда и только тогда, когда его hom-функтор Hom _C (–, Q ) точен .

Если $0\to Q\to U\to V\to 0$ представляет собой точную последовательность в $\mathbf {C}$ такой, что Q инъективен, то последовательность расщепляется .

Достаточно инъективных и инъективных оболочек

Категория $\mathbf {C}$ Говорят, что в нем достаточно инъектив , если для каждого объекта X из $\mathbf {C}$, существует мономорфизм X в инъективный объект.

Мономорфизм g в $\mathbf {C}$ называется существенным мономорфизмом, если для любого морфизма f композиция fg является мономорфизмом только в том случае, если f является мономорфизмом.

Если g существенный мономорфизм с областью X инъективной кообластью G , то G называется инъективной оболочкой X. — и Тогда инъективная оболочка определяется X однозначно с точностью до неканонического изоморфизма.

Примеры

• В категории абелевых групп и групповых гомоморфизмов Ab инъективный объект обязательно является делимой группой . Если принять аксиому выбора, то понятия эквивалентны.
• В категории (левых) модулей и гомоморфизмов модулей R — Mod инъективный объект является инъективным модулем . R - Mod имеет инъективные оболочки (как следствие, R - Mod имеет достаточно инъективных форм).
• В категории метрических пространств Met инъективный объект — это инъективное метрическое пространство , а инъективная оболочка метрического пространства — это его узкая оболочка .
• В категории T ₀ пространств и непрерывных отображений инъективный объект всегда является топологией Скотта на непрерывной решетке и, следовательно, всегда трезв и локально компактен .

Использует

Если в абелевой категории достаточно инъектив, мы можем формировать инъективные резольвенты , т. е. для данного объекта X мы можем сформировать длинную точную последовательность

$0\to X\to Q^{0}\to Q^{1}\to Q^{2}\to \cdots$

и затем можно определить производные функторы данного функтора F, применив F к этой последовательности и вычислив гомологии полученной (не обязательно точной) последовательности. Этот подход используется для определения функторов Ext и Tor , а также различных теорий когомологий в теории групп , алгебраической топологии и алгебраической геометрии . Используемые категории обычно представляют собой категории функторов или категории пучков O _X модулей в некотором кольцевом пространстве ( X , O _X ) или, в более общем смысле, любую категорию Гротендика .

Обобщение

Объект Q является H -инъективным, если для данного h : A → B в H любое f : A → Q факторизуется через h .

Позволять $\mathbf {C}$ быть категорией и пусть ${\mathcal {H}}$ быть классом морфизмов $\mathbf {C}$.

Объект $Q$ из $\mathbf {C}$ Говорят, что это ${\mathcal {H}}$-инъективен, если для любого морфизма $f:A\to Q$ и каждый морфизм $h:A\to B$ в ${\mathcal {H}}$ существует морфизм $g:B\to Q$ с $g\circ h=f$.

Если ${\mathcal {H}}$ — класс мономорфизмов , мы возвращаемся к инъективным объектам, которые рассматривались выше.

Категория $\mathbf {C}$ говорят, что достаточно ${\mathcal {H}}$-инъективны , если для каждого объекта X из $\mathbf {C}$, существует ${\mathcal {H}}$-морфизм из X в ${\mathcal {H}}$-инъективный объект.

А ${\mathcal {H}}$-морфизм g в $\mathbf {C}$ называется ${\mathcal {H}}$-существенно , если для любого морфизма f композиция fg находится в ${\mathcal {H}}$ только если f находится в ${\mathcal {H}}$.

Если g является ${\mathcal {H}}$-существенный морфизм с областью X и ${\mathcal {H}}$-инъективная кообласть G , то G называется ${\mathcal {H}}$-инъективная X . оболочка

Примеры H -инъективных объектов

• В категории симплициальных множеств инъективные объекты относительно класса ${\mathcal {H}}$ анодинных расширений являются кановскими комплексами .
• В категории частично упорядоченных множеств и монотонных отображений полные решетки образуют инъективные объекты класса ${\mathcal {H}}$ , вложений порядка а пополнение Дедекинда–МакНила частично упорядоченного множества — это его ${\mathcal {H}}$- инъективная оболочка.

См. также

• Проективный объект

Ссылки

• Иржи Адамек, Хорст Херрлих, Джордж Стрекер. Абстрактные и конкретные категории: «Радость кошек», глава 9, «Инъективные объекты и существенные вложения», переизданный в «Переизданиях и приложениях категорий», № 17 (2006), стр. 1–507 , Wiley (1990).
• Дж. Росицки, Инъективность и доступные категории
• Ф. Кальяри и С. Монтовани, T ₀ -отражение и инъективные оболочки расслоенных пространств