Группа контактов

В математике группа булавок — это некоторая подгруппа алгебры Клиффорда, связанная с квадратичным пространством . Он отображает 2-в-1 в ортогональную группу так же, как спиновая группа отображает 2-в-1 в специальную ортогональную группу .

В общем, отображение группы Пина в ортогональную группу не является сюръективным или универсальным накрывающим пространством , но если квадратичная форма определена (и размерность больше 2), то это и то, и другое.

Нетривиальный элемент ядра обозначается $-1,$ которое не следует путать с ортогональным преобразованием отражения через начало координат , обычно обозначаемым $-I.$

Общее определение

Позволять $V$ — векторное пространство с невырожденной квадратичной формой $Q$ . Группа контактов $\operatorname {Pin} (V,Q)$ является подмножеством алгебры Клиффорда $\operatorname {Cl} (V,Q)$ состоящее из элементов вида $v_{1}v_{2}\cdots v_{k}$ , где $v_{i}$ являются векторами такими, что $Q(v_{i})=\pm 1$ . Спиновая группа $\operatorname {Spin} (V,Q)$ определяется аналогично, но с $k$ ограничено, чтобы быть четным; это подгруппа группы контактов. ^[1]

В этой статье $V$ всегда является реальным векторным пространством. Когда $V$ имеет базисные векторы $e_{1},...,e_{p+q}$ удовлетворяющий $e_{1}^{2},...,e_{p}^{2}=1$ и $e_{p+1}^{2},...,e_{p+q}^{2}=-1,$ группа контактов обозначается Pin( p , q ).

Геометрически для векторов $v$ с $Q(v)\neq 0$ , $-vwv^{-1}$ является отражением вектора $w$ через гиперплоскость, ортогональную $v$ . В более общем смысле элемент $v_{1}v_{2}\cdots v_{k}$ группы контактов действует на векторы путем преобразования $w$ к $(-1)^{k}v_{1}v_{2}\cdots v_{k}w(v_{1}v_{2}\cdots v_{k})^{-1}$ , который представляет собой композицию k отражений. Поскольку каждое ортогональное преобразование может быть выражено как композиция отражений ( теорема Картана–Дьедонне ), отсюда следует, что это представление группы штифтов является гомоморфизмом группы штифтов на ортогональную группу. Это часто называют скрученным сопряженным представлением. Элементы ±1 группы выводов — это элементы, которые соответствуют идентификатору. $I\in O(p,q)$ , и каждый элемент O( p , q ) соответствует ровно двум элементам Pin( p , q ). ^[2]

Определенная форма

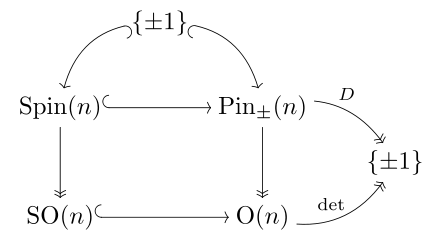
Группа выводов определенной формы отображается на ортогональную группу, причем каждый компонент односвязен (в размерности 3 и выше): он дважды покрывает ортогональную группу. Группы штифтов для положительно определенной квадратичной формы Q и для ее отрицательной - Q не изоморфны, а ортогональные группы - изоморфны. ^{[примечание 1]}

В терминах стандартных форм O( n , 0) = O(0, n ), но Pin( n , 0) и Pin(0, n ), вообще говоря, не изоморфны. Используя соглашение о знаках «+» для алгебр Клиффорда (где $v^{2}=Q(v)\in \mathrm {Cl} (V,Q)$ ), пишут

{\mbox{Pin}}_{+}(n):={\mbox{Pin}}(n,0)\qquad {\mbox{Pin}}_{-}(n):={\mbox{Pin}}(0,n)

и оба они отображаются на O( n ) = O( n , 0) = O(0, n ).

Напротив, мы имеем естественный изоморфизм ^{[примечание 2]} Spin( n , 0) ≅ Spin(0, n ), и оба они являются (уникальным) нетривиальным двойным покрытием специальной ортогональной группы SO( n ), которая является (уникальным) универсальным покрытием для n ≥ 3.

Неопределенная форма

Существует целых восемь различных двойных накрытий O( p , q ) для p , q ≠ 0, которые соответствуют расширениям центра (который является либо C ₂ × C ₂ , либо C ₄ ) с помощью C ₂ . Только две из них являются контактными группами — те, которые допускают алгебру Клиффорда в качестве представления . Они называются Pin( p , q ) и Pin( q , p ) соответственно.

Как топологическая группа

Каждая связная топологическая группа имеет уникальное универсальное накрытие в виде топологического пространства, которое имеет уникальную групповую структуру как центральное расширение фундаментальной группы. Для несвязной топологической группы существует единственное универсальное накрытие единичного компонента группы, и можно взять то же накрытие, что и топологические пространства на других компонентах (которые являются главными однородными пространствами для единичного компонента), но структура группы на другие компоненты не определяются однозначно.

Группы Pin и Spin представляют собой особые топологические группы, связанные с ортогональными и специальными ортогональными группами, происходящими из алгебр Клиффорда: существуют и другие подобные группы, соответствующие другим двойным накрытиям или другим групповым структурам на других компонентах, но они не называются как группы Pin или Spin, и особо не изучали.

В 2001 году Анджей Траутман ^{[примечание 3]} нашел набор всех 32 неэквивалентных двойных накрытий O( p ) x O( q ), максимальную компактную подгруппу O( p , q ) и явную конструкцию 8 двойных накрытий той же группы O( p , q ).

Строительство

Две группы контактов соответствуют двум центральным расширениям.

1\to \{\pm 1\}\to {\mbox{Pin}}_{\pm }(V)\to \mathrm {O} (V)\to 1.

Групповая структура на Spin( V ) (компонента связности определителя 1) уже определена; групповая структура другого компонента определена с точностью до центра и, таким образом, имеет неоднозначность ±1.

Два расширения различаются тем, соответствует ли прообраз отражения квадрату ±1 ∈ Ker (Spin( V ) → SO( V )), и две группы контактов называются соответственно. Явно отражение имеет порядок 2 по O( V ), r ² = 1, поэтому квадрат прообраза отражения (имеющего единицу определителя) должен находиться в ядре Spin _± ( V ) → SO( V ), поэтому ${\tilde {r}}^{2}=\pm 1$ , и любой выбор определяет группу выводов (поскольку все отражения сопряжены элементом SO( V ), который связан, все отражения должны иметь одно и то же значение).

Конкретно, в Pin ₊ , ${\tilde {r}}$ имеет порядок 2, а прообраз подгруппы {1, r } равен C ₂ × C ₂ : если одно и то же отражение повторяется дважды, получается тождество.

В Пин _— , ${\tilde {r}}$ имеет порядок 4, а прообраз подгруппы {1, r } равен C ₄ : если одно и то же отражение повторяется дважды, получается « поворот на 2π» — нетривиальный элемент Spin( V ) → SO( V ) можно интерпретировать как «поворот на 2π» (каждая ось дает один и тот же элемент).

Низкие размеры

В 1 измерении группы штифтов конгруэнтны первым двугранным и дициклическим группам:

{\begin{aligned}{\mbox{Pin}}_{+}(1)&\cong \mathrm {C} _{2}\times \mathrm {C} _{2}={\mbox{Dih}}_{1}\\{\mbox{Pin}}_{-}(1)&\cong \mathrm {C} _{4}={\mbox{Dic}}_{1}.\end{aligned}}

В двух измерениях различие между Pin ₊ и Pin ₋ отражает различие между группой диэдра 2 n -угольника и дициклической группой циклической группы C _{2 n} .

В Pin ₊ прообраз группы диэдра n -угольника, рассматриваемый как подгруппа Dih _n < O(2), является группой диэдра 2 n -угольника, Dih _{2 n} < Pin ₊ (2), а в Pin ₋ прообразом группы диэдра является дициклическая группа Dic _n < Pin ₋ (2).

Результирующий коммутативный квадрат подгрупп для Spin(2), Pin ₊ (2), SO(2), O(2) – а именно C _{2 n} , Dih _{2 n} , C _n , Dih _n – также получается с использованием проективного ортогонала группа (спускающаяся от O на 2-кратное частное, а не вверх на 2-кратное накрытие) в квадрате SO(2), O(2), PSO(2), PO(2), хотя в этом случае это также реализуется геометрически, поскольку «проективизация 2 n -угольника в круге является n -угольником на проективной прямой».

В 3 измерениях ситуация следующая. Алгебра Клиффорда, порожденная тремя антикоммутирующими квадратными корнями из +1, является алгеброй комплексных матриц размера 2×2, а Pin ₊ (3) изоморфна $\{A\in U(2):\det A=\pm 1\}$ . ^[3] Алгебра Клиффорда, порожденная тремя антикоммутирующими квадратными корнями из -1, называется алгеброй $\mathbb {H} \oplus \mathbb {H}$ , а Pin ₋ (3) изоморфен SU(2) × C ₂ . Эти группы неизоморфны, поскольку центром Pin ₊ (3) является C ₄ , а центром Pin ₋ (3) является C ₂ × C ₂ .

Центр

Предполагать $n>0$ . Центр $\mathrm {Pin} _{+}(n)$ является $\mathrm {C} _{2}\times \mathrm {C} _{2}$ когда $n=0,1\ \mathrm {mod} \ 4$ , и $\mathrm {C} _{4}$ когда $n=2,3\ \mathrm {mod} \ 4$ . Центр $\mathrm {Pin} _{-}(n)$ является $\mathrm {C} _{2}\times \mathrm {C} _{2}$ когда $n=0,3\ \mathrm {mod} \ 4$ , и $\mathrm {C} _{4}$ когда $n=2,1\ \mathrm {mod} \ 4$ .

Имя

Название было введено в ( Atiyah, Bott & Shapiro 1964 , стр. 3, строка 17), где говорится: «Эта шутка принадлежит Дж. П. Серру ».Это обратная формация от Spin: «Pin относится к O( n ) так же, как Spin относится к SO( n )», следовательно, удаление «S» из «Spin» дает «Pin».

Примечания

^ Фактически, они равны как подмножества GL( V ), а не просто изоморфны как абстрактные группы: оператор сохраняет форму тогда и только тогда, когда он сохраняет отрицательную форму.
^ Они входят в разные алгебры. $\mathrm {Cl} (n,0)\not \cong \mathrm {Cl} (0,n)$ , но они равны как подмножества векторных пространств $\mathrm {Cl} (n,0)=\mathrm {Cl} (0,n)=\Lambda ^{*}\mathbf {R} ^{n}$ и имеют одинаковую структуру продукта, поэтому они естественным образом идентифицируются.
^ А. Траутман (2001). «Двойные накрытия псевдоортогональных групп». У Ф. Браккса; JSR Чисхолм; В. Соучек (ред.). Анализ Клиффорда и его приложения . Научная серия НАТО. Том. 25. С. 377–388. дои : 10.1007/978-94-010-0862-4_32 . ISBN 978-0-7923-7045-1 .

Ссылки

^ Лоусон и Михельсон 1989 , с. 18
^ Лоусон и Михельсон, 1989 , стр. 16–20.
^ Харви 1990 , с. 302

Атья, Миссури ; Ботт, Р .; Шапиро, А. (1964), «Модули Клиффорда», Топология , 3, доп. 1: 3–38, дои : 10.1016/0040-9383(64)90003-5
М. Каруби (1968). «Алгебры Клиффорда и К-теория» . Энн. наук. Эк. Норм. Большой . 1 (2): 161–270. дои : 10.24033/asens.1163 .
Дабровский, Л. (1988), Групповые действия на спинорах , Библиополис, ISBN 88-7088-205-5
Карлип, С.; ДеВитт-Моретт, К. (1988), «Там, где знак метрики имеет значение», Phys. Преподобный Летт. , 60 (16): 1599–1601, Bibcode : 1988PhRvL..60.1599C , doi : 10.1103/physrevlett.60.1599 , PMID 10038088
Чамблин, А. (1994), «О препятствиях к неклиффордовым стержневым структурам», Comm. Математика. Физ. , 164 (1): 65–85, arXiv : gr-qc/9509039 , Bibcode : 1994CMaPh.164...65C , doi : 10.1007/bf02108806 , S2CID 18305909
Харви, Ф. Риз (1990), Спиноры и калибровки , Academic Press, ISBN 978-0-12-329650-4
Лоусон, Х. Блейн; Мишельсон, Мария-Луиза (1989). Спиновая геометрия . Издательство Принстонского университета . ISBN 978-0-691-08542-5 .
Каруби, Макс (2008). К-теория . Спрингер. стр. 212–214. ISBN 978-3-540-79889-7 .

[3] Фактически, они равны как подмножества GL( V ), а не просто изоморфны как абстрактные группы: оператор сохраняет форму тогда и только тогда, когда он сохраняет отрицательную форму.

[4] Они входят в разные алгебры. $\mathrm {Cl} (n,0)\not \cong \mathrm {Cl} (0,n)$ , но они равны как подмножества векторных пространств $\mathrm {Cl} (n,0)=\mathrm {Cl} (0,n)=\Lambda ^{*}\mathbf {R} ^{n}$ и имеют одинаковую структуру продукта, поэтому они естественным образом идентифицируются.

[5] А. Траутман (2001). «Двойные накрытия псевдоортогональных групп». У Ф. Браккса; JSR Чисхолм; В. Соучек (ред.). Анализ Клиффорда и его приложения . Научная серия НАТО. Том. 25. С. 377–388. дои : 10.1007/978-94-010-0862-4_32 . ISBN 978-0-7923-7045-1 .

[1] Лоусон и Михельсон 1989 , с. 18

[2] Лоусон и Михельсон, 1989 , стр. 16–20.

[6] Харви 1990 , с. 302

[1]

[2]

[примечание 1]

[примечание 2]

[примечание 3]

[3]

v т и Симметрии C, P и T
C-симметрия P-симметрия Т-симметрия
КП CP-симметрия CPT-симметрия
Хиральность Группа контактов Симметрия (физика)