Метод прямой жесткости

В качестве одного из методов структурного анализа метод прямой жесткости , также известный как метод матричной жесткости , особенно подходит для автоматизированного компьютерного анализа сложных конструкций, включая статически неопределимый тип. Это матричный метод, который использует соотношения жесткости элементов для расчета сил и смещений элементов в конструкциях. Метод прямой жесткости является наиболее распространенной реализацией метода конечных элементов (МКЭ). При применении метода систему необходимо моделировать как совокупность более простых идеализированных элементов, связанных между собой в узлах. Свойства жесткости материала этих элементов затем с помощью матричной математики компилируются в одно матричное уравнение, которое управляет поведением всей идеализированной конструкции. Затем неизвестные перемещения и силы конструкции можно определить путем решения этого уравнения. Метод прямой жесткости составляет основу большинства коммерческих и бесплатных программ для конечных элементов.

Метод прямой жесткости зародился в области аэрокосмической промышленности . Исследователи рассмотрели различные подходы к анализу сложных каркасов самолетов. К ним относятся теория упругости , энергетические принципы в строительной механике , метод гибкости и метод матричной жесткости . Именно благодаря анализу этих методов метод прямой жесткости стал эффективным методом, идеально подходящим для компьютерной реализации.

История

Между 1934 и 1938 годами А. Р. Коллар и У. Дж. Дункан опубликовали первые статьи с представлением и терминологией матричных систем, которые используются сегодня. Исследования аэроупругости продолжались во время Второй мировой войны , но ограничения на публикацию с 1938 по 1947 год затрудняют отслеживание этой работы. Второй крупный прорыв в матричном структурном анализе произошел в 1954 и 1955 годах, когда профессор Джон Х. Аргирис систематизировал концепцию сборки элементарных компонентов конструкции в систему уравнений. Наконец, 6 ноября 1959 года М. Дж. Тернер , глава подразделения структурной динамики компании Boeing , опубликовал статью, в которой излагался метод прямой жесткости как эффективная модель для компьютерной реализации ( Фелиппа, 2001 ).

Отношения жесткости стержня

Типичное соотношение жесткости стержня имеет следующую общую форму:

$\mathbf {Q} ^{m}=\mathbf {k} ^{m}\mathbf {q} ^{m}+\mathbf {Q} ^{om}$ ( 1 )

где

m = номер участника m .

$\mathbf {Q} ^{m}$ = вектор характеристических сил стержня, которые являются неизвестными внутренними силами.

$\mathbf {k} ^{m}$ = матрица жесткости элемента, характеризующая устойчивость элемента к деформациям.

$\mathbf {q} ^{m}$ = вектор характерных перемещений или деформаций элемента.

$\mathbf {Q} ^{om}$ = вектор характеристических сил стержня, вызванных внешними воздействиями (такими как известные силы и изменения температуры), приложенными к стержню, пока $\mathbf {q} ^{m}=0$.

Если $\mathbf {q} ^{m}$ являются деформациями стержней, а не абсолютными перемещениями, тогда $\mathbf {Q} ^{m}$ являются независимыми силами стержня, и в таком случае (1) можно инвертировать, чтобы получить так называемую матрицу гибкости стержня , которая используется в методе гибкости .

Соотношение жесткости системы

См. Также: Матрица жесткости.

Для системы со многими элементами, соединенными между собой в точках, называемых узлами, соотношения жесткости элементов, такие как уравнение (1), можно интегрировать, используя следующие наблюдения:

• Деформации элемента $\mathbf {q} ^{m}$ может быть выражено через узловые перемещения системы r , чтобы обеспечить совместимость между элементами. Это означает, что r будет первичными неизвестными.
• Членские силы $\mathbf {Q} ^{m}$ помогают удерживать узлы в равновесии под действием узловых сил R . Это означает, что правая часть (1) будет интегрирована в правую часть следующих узловых уравнений равновесия для всей системы:

$\mathbf {R} =\mathbf {Kr} +\mathbf {R} ^{o}$ ( 2 )

где

$\mathbf {R}$ = вектор узловых сил, представляющий внешние силы, приложенные к узлам системы.

$\mathbf {K}$ = матрица жесткости системы, которая определяется путем сборки матриц жесткости элементов. $\mathbf {k} ^{m}$.

$\mathbf {r}$ = вектор узловых перемещений системы, который может определять все возможные деформированные конфигурации системы под действием произвольных узловых сил R .

$\mathbf {R} ^{o}$ = вектор эквивалентных узловых сил, представляющий все внешние воздействия, кроме узловых сил, которые уже включены в предыдущий вектор узловых сил R . Этот вектор устанавливается путем объединения членов $\mathbf {Q} ^{om}$.

Решение

Матрица жесткости системы K является квадратной, поскольку векторы R и r имеют одинаковый размер. Кроме того, оно симметрично, поскольку $\mathbf {k} ^{m}$ является симметричным. После учета ограничений опор в (2) узловые перемещения находятся путем решения системы линейных уравнений (2) в символическом виде:

$\mathbf {r} =\mathbf {K} ^{-1}(\mathbf {R} -\mathbf {R} ^{o})\qquad \qquad \qquad \mathrm {(3)}$

Впоследствии характеристические силы элементов можно найти из уравнения (1), где $\mathbf {q} ^{m}$ может быть найден из r путем рассмотрения совместимости.

Метод прямой жесткости

Обычно уравнение (1) принимают в форме, где $\mathbf {q} ^{m}$ и $\mathbf {Q} ^{om}$ представляют собой соответственно перемещения концов стержня и силы, совпадающие по направлению с r и R . В таком случае $\mathbf {K}$ и $\mathbf {R} ^{o}$ может быть получено путем прямого суммирования матриц членов $\mathbf {k} ^{m}$ и $\mathbf {Q} ^{om}$. Этот метод тогда известен как метод прямой жесткости.

Преимущества и недостатки метода матричной жесткости сравниваются и обсуждаются в статье о методе гибкости .

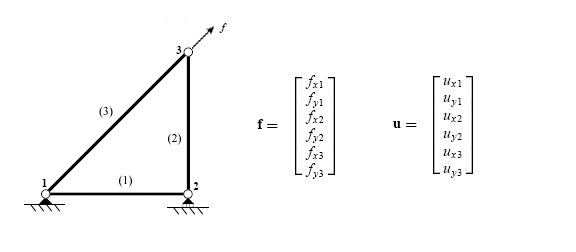
Пример

Авария

Первым шагом при использовании метода прямой жесткости является идентификация отдельных элементов, составляющих конструкцию.

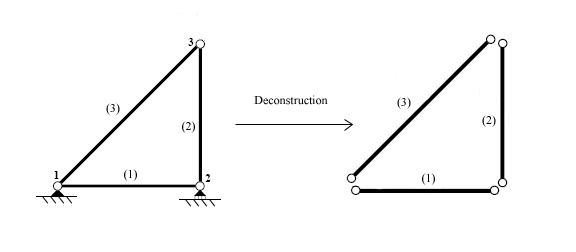
Как только элементы идентифицированы, структура разъединяется в узлах, точках, которые соединяют различные элементы вместе.

Затем каждый элемент анализируется индивидуально для разработки уравнений жесткости элемента. Силы и перемещения связаны через матрицу жесткости элемента, которая зависит от геометрии и свойств элемента.

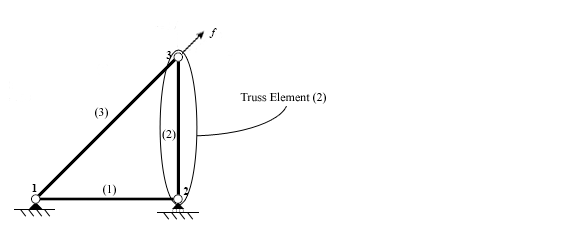
Элемент фермы может передавать силы только при сжатии или растяжении. Это означает, что в двух измерениях каждый узел имеет две степени свободы (ГРИП): горизонтальное и вертикальное смещение. Полученное уравнение содержит матрицу жесткости размером четыре на четыре.

${\begin{bmatrix}f_{x1}\\f_{y1}\\f_{x2}\\f_{y2}\\\end{bmatrix}}={\begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}\\k_{21}&k_{22}&k_{23}&k_{24}\\k_{31}&k_{32}&k_{33}&k_{34}\\k_{41}&k_{42}&k_{43}&k_{44}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\u_{x2}\\u_{y2}\\\end{bmatrix}}$

Элемент рамы способен выдерживать не только сжатие и растяжение, но и изгибающие моменты. Это приводит к трем степеням свободы: горизонтальному смещению, вертикальному смещению и вращению в плоскости. Матрица жесткости в данном случае равна шесть на шесть.

${\begin{bmatrix}f_{x1}\\f_{y1}\\m_{z1}\\f_{x2}\\f_{y2}\\m_{z2}\\\end{bmatrix}}={\begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}&k_{15}&k_{16}\\k_{21}&k_{22}&k_{23}&k_{24}&k_{25}&k_{26}\\k_{31}&k_{32}&k_{33}&k_{34}&k_{35}&k_{36}\\k_{41}&k_{42}&k_{43}&k_{44}&k_{45}&k_{46}\\k_{51}&k_{52}&k_{53}&k_{54}&k_{55}&k_{56}\\k_{61}&k_{62}&k_{63}&k_{64}&k_{65}&k_{66}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\\theta _{z1}\\u_{x2}\\u_{y2}\\\theta _{z2}\\\end{bmatrix}}$

Другие элементы, такие как пластины и оболочки, также могут быть включены в прямой метод жесткости, и необходимо разработать аналогичные уравнения.

Сборка

После разработки соотношений жесткости отдельных элементов их необходимо собрать в исходную конструкцию. Первым шагом в этом процессе является преобразование соотношений жесткости для отдельных элементов в глобальную систему для всей конструкции. В случае элемента фермы глобальная форма метода жесткости зависит от угла элемента по отношению к глобальной системе координат (обычно это традиционная декартова система координат ).

${\begin{bmatrix}f_{x1}\\f_{y1}\\f_{x2}\\f_{y2}\\\end{bmatrix}}={\frac {EA}{L}}{\begin{bmatrix}c^{2}&sc&-c^{2}&-sc\\sc&s^{2}&-sc&-s^{2}\\-c^{2}&-sc&c^{2}&sc\\-sc&-s^{2}&sc&s^{2}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\u_{x2}\\u_{y2}\\\end{bmatrix}}{\begin{array}{r }s=\sin \beta \\c=\cos \beta \\\end{array}}$ (для элемента фермы под углом β) Эквивалентно, ${\begin{bmatrix}f_{x1}\\f_{y1}\\\hline f_{x2}\\f_{y2}\end{bmatrix}}={\frac {EA}{L}}\left[{\begin{array}{c c|c c}c_{x}c_{x}&c_{x}c_{y}&-c_{x}c_{x}&-c_{x}c_{y}\\c_{y}c_{x}&c_{y}c_{y}&-c_{y}c_{x}&-c_{y}c_{y}\\\hline -c_{x}c_{x}&-c_{x}c_{y}&c_{x}c_{x}&c_{x}c_{y}\\-c_{y}c_{x}&-c_{y}c_{y}&c_{y}c_{x}&c_{y}c_{y}\\\end{array}}\right]{\begin{bmatrix}u_{x1}\\u_{y1}\\\hline u_{x2}\\u_{y2}\end{bmatrix}}$

где $c_{x}$ и $c_{y}$ — это направляющие косинусы элемента фермы (т. е. они являются компонентами единичного вектора, совмещенного с элементом). Эта форма показывает, как обобщить жесткость элемента на трехмерные пространственные фермы, просто расширив шаблон, который очевиден в этой формулировке.

После разработки матрицы жесткости элементов в глобальной системе координат их необходимо объединить в единую «главную» или «глобальную» матрицу жесткости. При объединении этих матриц необходимо соблюдать два правила: совместимость перемещений и равновесие сил в каждом узле. Эти правила поддерживаются путем сопоставления узловых смещений элементов с глобальными узловыми смещениями.

Векторы глобального смещения и силы содержат по одной записи для каждой степени свободы в конструкции. Матрицы жесткости элементов объединяются путем увеличения или расширения каждой матрицы в соответствии с глобальными векторами смещения и нагрузки.

$k^{(1)}={\frac {EA}{L}}{\begin{bmatrix}1&0&-1&0\\0&0&0&0\\-1&0&1&0\\0&0&0&0\\\end{bmatrix}}\rightarrow K^{(1)}={\frac {EA}{L}}{\begin{bmatrix}1&0&-1&0&0&0\\0&0&0&0&0&0\\-1&0&1&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\\end{bmatrix}}$(для элемента (1) вышеуказанной структуры)

Наконец, глобальная матрица жесткости строится путем сложения отдельных матриц расширенных элементов.

Решение

После того как глобальная матрица жесткости, вектор перемещения и вектор силы построены, систему можно выразить в виде одного матричного уравнения.

Для каждой степени свободы в конструкции известно либо смещение, либо сила.

После ввода известного значения для каждой степени свободы основное уравнение жесткости будет завершено и готово к оценке. Существует несколько различных методов оценки матричного уравнения, включая, помимо прочего, разложение Холецкого и грубую оценку систем уравнений. Если конструкция не закреплена должным образом, приложение силы заставит ее двигаться жестко, и необходимо добавить дополнительные условия поддержки.

Метод, описанный в этом разделе, представляет собой обзор метода прямой жесткости. Для получения более подробной информации о процессе, а также предположений о свойствах материала, присущих этому процессу, следует обращаться к дополнительным источникам.

Приложения

Метод прямой жесткости был разработан специально для эффективного и простого внедрения в компьютерное программное обеспечение для оценки сложных конструкций, содержащих большое количество элементов. Сегодня почти каждый доступный решатель методом конечных элементов основан на методе прямой жесткости. Хотя каждая программа использует один и тот же процесс, многие из них были оптимизированы для сокращения времени вычислений и уменьшения требуемой памяти. Для этого были разработаны ярлыки.

Одной из крупнейших областей использования метода прямой жесткости является область структурного анализа, где этот метод был включен в программное обеспечение для моделирования. Программное обеспечение позволяет пользователям моделировать конструкцию, и после того, как пользователь определяет свойства материала элементов, программа автоматически генерирует элементы и глобальные соотношения жесткости. При применении различных условий нагрузки программное обеспечение оценивает конструкцию и генерирует прогибы для пользователя.

См. также

• Метод конечных элементов
• Метод конечных элементов в строительной механике
• Структурный анализ
• Гибкий метод
• Список пакетов программного обеспечения для конечных элементов

Внешние ссылки

• Применение метода прямой жесткости к одномерной пружинной системе
• Матричный структурный анализ
• Анимация моделирования анализа жесткости

Ссылки

• Фелиппа, Карлос А. (2001), «Исторический очерк матричного структурного анализа: пьеса в трех действиях» (PDF) , Computers & Structures , 79 (14): 1313–1324, doi : 10.1016/S0045-7949(01) )00025-6 , ISSN   0045-7949 , заархивировано из оригинала (PDF) 29 июня 2007 г. , получено 5 октября 2005 г.
• Фелиппа, Карлос А. Введение в метод конечных элементов. Осень 2001 г. Университет Колорадо. 18 сентября 2005 г.
• Робинсон, Джон. Структурный матричный анализ для инженера. Нью-Йорк: Джон Уайли и сыновья, 1966.
• Рубинштейн, Моше Ф. Матричный компьютерный анализ структур. Нью-Джерси: Прентис-Холл, 1966 г.
• МакГуайр В., Галлахер Р.Х. и Цимиан Р.Д. Матричный структурный анализ, 2-е изд. Нью-Йорк: Джон Уайли и сыновья, 2000.