Метод прямой жесткости

В качестве одного из методов структурного анализа метод прямой жесткости , также известный как метод жесткости матрицы , особенно подходит для компьютерного анализа сложных структур, включая статически неопределенный тип. Это матричный метод, который использует отношения с жесткостью членов для вычисления сил членов и смещений в структурах. Метод прямой жесткости является наиболее распространенной реализацией метода конечных элементов (FEM). При применении метода система должна быть смоделирована как набор более простых, идеализированных элементов, связанных с узлами. Свойства жесткости материала этих элементов затем посредством матричной математики , составленной в одно матричное уравнение, которое регулирует поведение всей идеализированной структуры. Неизвестные смещения и силы структуры могут быть определены путем решения этого уравнения. Метод прямой жесткости образует основу для большинства коммерческих и бесплатных источника конечных элементов.

Метод прямой жесткости возник в области аэрокосмической промышленности . Исследователи смотрели на различные подходы для анализа сложных рамок самолета. Они включали теорию эластичности , энергетические принципы в структурной механике , метод гибкости и метод жесткости матрицы . Именно посредством анализа этих методов метод прямой жесткости появился как эффективный метод, идеально подходящий для компьютерной реализации.

История

Между 1934 и 1938 годами AR воротник и WJ Duncan опубликовали первые статьи с представлением и терминологией для матричных систем, которые используются сегодня. Аэроупругие исследования продолжались через Второй мировой войны , но ограничения публикации с 1938 по 1947 год затрудняют отслеживание этой работы. Второй основной прорыв в матричном структурном анализе произошел в течение 1954 и 1955 годов, когда профессор Джон Х. Аргирис систематизировал концепцию сборки элементарных компонентов структуры в систему уравнений. Наконец, 6 ноября 1959 года MJ Turner , руководителя конструктивной динамики Boeing , опубликовал статью, в котором рассказывается о методе прямой жесткости в качестве эффективной модели для компьютерной реализации ( Felippa 2001 ).

Отношения с жесткостью члена

Типичная связь с жесткостью члена имеет следующую общую форму:

\mathbf {Q} ^{m}=\mathbf {k} ^{m}\mathbf {q} ^{m}+\mathbf {Q} ^{om}

( 1 )

где

m = номер члена m .

\mathbf {Q} ^{m}

= вектор характерных сил члена, которые являются неизвестными внутренними силами.

\mathbf {k} ^{m}

= Матрица жесткости члена, которая характеризует сопротивление члена против деформаций.

\mathbf {q} ^{m}

= вектор характерных смещений или деформаций члена.

\mathbf {Q} ^{om}

= вектор характерных сил члена, вызванные внешними эффектами (такими как известные силы и изменения температуры), применяемые к члену, когда

\mathbf {q} ^{m}=0

.

Если $\mathbf {q} ^{m}$ деформации членов, а не абсолютные смещения, тогда $\mathbf {Q} ^{m}$ являются независимыми силами членов, и в таком случае (1) могут быть инвертированы, чтобы получить так называемую матрицу гибкости элемента , которая используется в методе гибкости .

Системная жесткость соотношения

Для системы со многими членами, связанными с точками, называемыми узлами, отношения с жесткостью членов, такие как уравнение (1), могут быть интегрированы, используя следующие наблюдения:

Деформации участника $\mathbf {q} ^{m}$ может быть выражен в терминах системы узлов r для обеспечения совместимости между членами. Это означает, что R будет основным неизвестным.
Силы -члены $\mathbf {Q} ^{m}$ Помогите сохранить узлы в равновесии под узловыми силами r . Это подразумевает, что правая сторона (1) будет интегрирована в правую сторону следующих уравнений узлового равновесия для всей системы:

\mathbf {R} =\mathbf {Kr} +\mathbf {R} ^{o}

( 2 )

где

\mathbf {R}

= вектор узловых сил, представляющих внешние силы, применяемые к узлам системы.

\mathbf {K}

= Матрица жесткости системы, которая устанавливается путем сборки матриц жесткости членов

\mathbf {k} ^{m}

.

\mathbf {r}

= вектор узловых смещений системы, которые могут определить все возможные деформированные конфигурации системы, подверженные произвольным узловым силам r .

\mathbf {R} ^{o}

= вектор эквивалентных узловых сил, представляющих все внешние эффекты, кроме узловых сил, которые уже включены в предыдущий вектор узловой силы r . Этот вектор устанавливается путем сборки членов

\mathbf {Q} ^{om}

.

Решение

Матрица жесткости системы k является квадратной, поскольку векторы R и R имеют одинаковый размер. Кроме того, это симметрично, потому что $\mathbf {k} ^{m}$ симметричный. После того, как ограничения поддержки учитываются в (2), узловые смещения обнаруживаются путем решения системы линейных уравнений (2), символически:

\mathbf {r} =\mathbf {K} ^{-1}(\mathbf {R} -\mathbf {R} ^{o})\qquad \qquad \qquad \mathrm {(3)}

Впоследствии характерные силы членов могут быть найдены из уравнения (1), где $\mathbf {q} ^{m}$ может быть найдено из R путем соображения совместимости.

Метод прямой жесткости

Обычно иметь уравнение (1) в форме, где $\mathbf {q} ^{m}$ и $\mathbf {Q} ^{om}$ соответственно, перемещения и силы в конце члена и силы, соответствующие направлению с r и r . В таком случае, $\mathbf {K}$ и $\mathbf {R} ^{o}$ можно получить путем прямого суммирования матриц членов $\mathbf {k} ^{m}$ и $\mathbf {Q} ^{om}$ Полем Затем метод известен как метод прямой жесткости.

Преимущества и недостатки метода жесткости матрицы сравниваются и обсуждаются в статье метода гибкости .

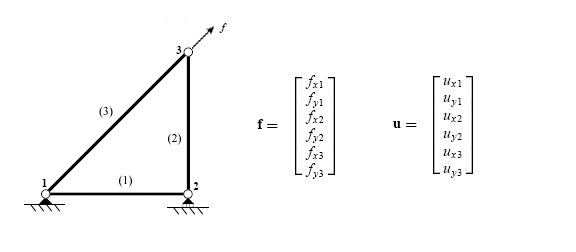
Пример

Авария

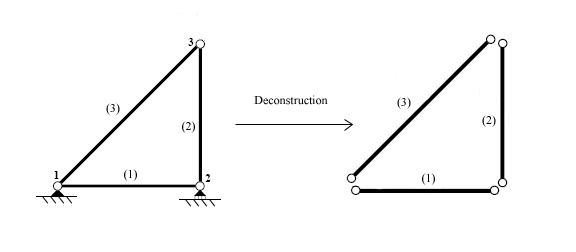
Первым шагом при использовании метода прямой жесткости является определение отдельных элементов, которые составляют структуру.

Как только элементы идентифицируются, структура отключается в узлах, точки, которые соединяют различные элементы вместе.

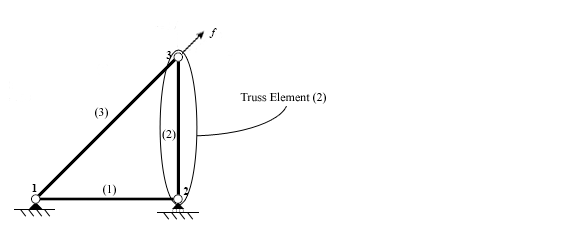
Затем каждый элемент анализируется индивидуально для разработки уравнений жесткости члена. Силы и смещения связаны с помощью матрицы жесткости элемента, которая зависит от геометрии и свойств элемента.

Элемент фермы может передавать только силы в сжатии или натяжении. Это означает, что в двух измерениях каждый узел имеет две степени свободы (DOF): горизонтальное и вертикальное смещение. Полученное уравнение содержит матрицу четырех на четыре жесткости.

${\begin{bmatrix}f_{x1}\\f_{y1}\\f_{x2}\\f_{y2}\\\end{bmatrix}}={\begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}\\k_{21}&k_{22}&k_{23}&k_{24}\\k_{31}&k_{32}&k_{33}&k_{34}\\k_{41}&k_{42}&k_{43}&k_{44}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\u_{x2}\\u_{y2}\\\end{bmatrix}}$

Элемент рамы способен выдерживать изгибающие моменты в дополнение к сжатию и натяжению. Это приводит к три степени свободы: горизонтальное смещение, вертикальное смещение и вращение плоскости. Матрица жесткости в этом случае составляет шесть на шесть.

${\begin{bmatrix}f_{x1}\\f_{y1}\\m_{z1}\\f_{x2}\\f_{y2}\\m_{z2}\\\end{bmatrix}}={\begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}&k_{15}&k_{16}\\k_{21}&k_{22}&k_{23}&k_{24}&k_{25}&k_{26}\\k_{31}&k_{32}&k_{33}&k_{34}&k_{35}&k_{36}\\k_{41}&k_{42}&k_{43}&k_{44}&k_{45}&k_{46}\\k_{51}&k_{52}&k_{53}&k_{54}&k_{55}&k_{56}\\k_{61}&k_{62}&k_{63}&k_{64}&k_{65}&k_{66}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\\theta _{z1}\\u_{x2}\\u_{y2}\\\theta _{z2}\\\end{bmatrix}}$

Другие элементы, такие как пластины и оболочки, также могут быть включены в метод прямой жесткости, и должны быть разработаны аналогичные уравнения.

Сборка

Как только индивидуальные отношения с жесткостью элемента были разработаны, они должны быть собраны в исходную структуру. Первым шагом в этом процессе является преобразование отношений жесткости для отдельных элементов в глобальную систему для всей структуры. В случае элемента фермы глобальная форма метода жесткости зависит от угла элемента относительно глобальной системы координат (эта система обычно является традиционной декартовой системой координат ).

${\begin{bmatrix}f_{x1}\\f_{y1}\\f_{x2}\\f_{y2}\\\end{bmatrix}}={\frac {EA}{L}}{\begin{bmatrix}c^{2}&sc&-c^{2}&-sc\\sc&s^{2}&-sc&-s^{2}\\-c^{2}&-sc&c^{2}&sc\\-sc&-s^{2}&sc&s^{2}\\\end{bmatrix}}{\begin{bmatrix}u_{x1}\\u_{y1}\\u_{x2}\\u_{y2}\\\end{bmatrix}}{\begin{array}{r }s=\sin \beta \\c=\cos \beta \\\end{array}}$ (Для элемента фермы под углом β) Эквивалентно, ${\begin{bmatrix}f_{x1}\\f_{y1}\\\hline f_{x2}\\f_{y2}\end{bmatrix}}={\frac {EA}{L}}\left[{\begin{array}{c c|c c}c_{x}c_{x}&c_{x}c_{y}&-c_{x}c_{x}&-c_{x}c_{y}\\c_{y}c_{x}&c_{y}c_{y}&-c_{y}c_{x}&-c_{y}c_{y}\\\hline -c_{x}c_{x}&-c_{x}c_{y}&c_{x}c_{x}&c_{x}c_{y}\\-c_{y}c_{x}&-c_{y}c_{y}&c_{y}c_{x}&c_{y}c_{y}\\\end{array}}\right]{\begin{bmatrix}u_{x1}\\u_{y1}\\\hline u_{x2}\\u_{y2}\end{bmatrix}}$

где $c_{x}$ и $c_{y}$ Являются ли направление косинусов элемента фермы (то есть они являются компонентами единичного вектора, совместимых с элементом). Эта форма показывает, как обобщать жесткость элемента до трехмерных космических ферм, просто расширив шаблон, который очевиден в этой формулировке.

После разработки матрицы жесткости элемента в глобальной системе координат они должны быть объединены в единую матрицу жесткости «мастер» или «глобальная». При объединении этих матриц вместе существуют два правила: совместимость смещений и силового равновесия в каждом узле. Эти правила поддерживаются путем связи элемента узловых смещений с глобальными узловыми смещениями.

Каждый из глобальных перемещения и силовых векторов содержат одну запись для каждой степени свободы в структуре. Матрицы жесткости элемента объединяются путем увеличения или расширения каждой матрицы в конформации с глобальным смещением и нагрузки.

$k^{(1)}={\frac {EA}{L}}{\begin{bmatrix}1&0&-1&0\\0&0&0&0\\-1&0&1&0\\0&0&0&0\\\end{bmatrix}}\rightarrow K^{(1)}={\frac {EA}{L}}{\begin{bmatrix}1&0&-1&0&0&0\\0&0&0&0&0&0\\-1&0&1&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\\end{bmatrix}}$ (Для элемента (1) из вышеуказанной структуры)

Наконец, глобальная матрица жесткости построена путем добавления отдельных матриц расширенных элементов.

Решение

После того, как глобальная матрица жесткости, вектор смещения и вектор силы была построена, система может быть выражена в виде единого матричного уравнения.

Для каждой степени свободы в структуре известно либо смещение, либо сила.

После вставки известного значения для каждой степени свободы уравнение главной жесткости завершено и готово к оценке. Существует несколько различных методов, доступных для оценки матричного уравнения, включая, помимо прочего, декомпозиция Хоулесского и оценку грубой силы систем уравнений. Если структура не ограничена надлежащим образом, применение силы приведет к жесткому движению, и должны быть добавлены дополнительные условия поддержки.

Метод, описанный в этом разделе, предназначен как обзор метода прямой жесткости. Дополнительные источники следует обратиться к более подробной информации о процессе, а также о допущениях о свойствах материала, присущих процессу.

Приложения

Метод прямой жесткости был разработан специально для эффективного и легко реализованного в компьютерное программное обеспечение для оценки сложных структур, которые содержат большое количество элементов. Сегодня почти каждый доступный решатель конечных элементов основан на методе прямой жесткости. В то время как каждая программа использует один и тот же процесс, многие из них были упорядочены, чтобы сократить время вычисления и сократить необходимую память. Чтобы достичь этого, были разработаны ярлыки.

Одной из крупнейших областей для использования метода прямой жесткости является область структурного анализа, где этот метод был включен в программное обеспечение для моделирования. Программное обеспечение позволяет пользователям моделировать структуру, и после того, как пользователь определяет свойства материала элементов, программа автоматически генерирует отношения элемента и глобальные отношения жесткости. Когда применяются различные условия загрузки, программное обеспечение оценивает структуру и генерирует отклонения для пользователя.

Смотрите также

Внешние ссылки

Ссылки

Фелиппа, Карлос А. (2001), «Исторический контур матричного структурного анализа: игра в трех актах» (PDF) , компьютеры и структуры , 79 (14): 1313–1324, doi : 10.1016/s0045-7949 (01 ) 00025-6 , ISSN 0045-7949 , архивировано из оригинала (PDF) 2007-06-29 , извлеченные 2005-10-05
Фелиппа, Карлос А. Введение в метод конечных элементов. Осень 2001 г. Университет Колорадо. 18 сентября 2005 г.
Робинсон, Джон. Анализ структурной матрицы для инженера. Нью -Йорк: John Wiley & Sons, 1966
Рубинштейн, Моше Ф. Матричный компьютерный анализ структур. Нью-Джерси: Прентис-Холл, 1966
McGuire, W., Gallagher, RH и Ziemian, RD Matrix Структурный анализ, 2 -е изд. Нью -Йорк: John Wiley & Sons, 2000.