t-распределенное стохастическое встраивание соседей

t-распределенное стохастическое внедрение соседей ( t-SNE ) — это статистический метод визуализации многомерных данных путем присвоения каждой точке данных местоположения на двухмерной или трехмерной карте. Он основан на методе стохастического встраивания соседей, первоначально разработанном Джеффри Хинтоном и Сэмом Роуэйсом. ^{[ 1 ]} где Лоренс ван дер Маатен предложил t -распределенный вариант. ^{[ 2 ]} Это метод нелинейного уменьшения размерности , позволяющий встраивать многомерные данные для визуализации в низкомерное двух- или трехмерное пространство. В частности, он моделирует каждый многомерный объект с помощью двух- или трехмерной точки таким образом, что похожие объекты моделируются близлежащими точками, а разнородные объекты моделируются удаленными точками с высокой вероятностью.

Алгоритм t-SNE состоит из двух основных этапов. Во-первых, t-SNE строит распределение вероятностей по парам многомерных объектов таким образом, что сходным объектам присваивается более высокая вероятность, а разным точкам — меньшая вероятность. Во-вторых, t-SNE определяет аналогичное распределение вероятностей по точкам на низкоразмерной карте и минимизирует расхождение Кульбака-Лейблера (расхождение KL) между двумя распределениями относительно местоположения точек на карте. Хотя исходный алгоритм использует евклидово расстояние между объектами в качестве основы показателя сходства, его можно изменить при необходимости. Риманов — вариант UMAP .

t-SNE использовался для визуализации в широком спектре приложений, включая геномику , компьютерной безопасности , исследования ^{[ 3 ]} обработка естественного языка , анализ музыки , ^{[ 4 ]} исследования рака , ^{[ 5 ]} биоинформатика , ^{[ 6 ]} интерпретация геологической области, ^{[ 7 ]}^{[ 8 ]}^{[ 9 ]} и биомедицинская обработка сигналов. ^{[ 10 ]}

Для набора данных из n элементов t-SNE выполняется за $O(n 2)$ времени и требует $O(n 2)$ космос. ^{[ 11 ]}

Подробности

Учитывая набор $N$ многомерные объекты $\mathbf {x} _{1},\dots ,\mathbf {x} _{N}$ , t-SNE сначала вычисляет вероятности $p_{ij}$ пропорциональны сходству объектов $\mathbf {x} _{i}$ и $\mathbf {x} _{j}$ , следующее.

Для $i\neq j$ , определять

p_{j\mid i}={\frac {\exp(-\lVert \mathbf {x} _{i}-\mathbf {x} _{j}\rVert ^{2}/2\sigma _{i}^{2})}{\sum _{k\neq i}\exp(-\lVert \mathbf {x} _{i}-\mathbf {x} _{k}\rVert ^{2}/2\sigma _{i}^{2})}}

и установить $p_{i\mid i}=0$ . Обратите внимание, что приведенный выше знаменатель обеспечивает $\sum _{j}p_{j\mid i}=1$ для всех $i$ .

Как объяснили ван дер Маатен и Хинтон: «Сходство точек данных $x_{j}$ к точке данных $x_{i}$ – условная вероятность, $p_{j|i}$ , что $x_{i}$ выбрал бы $x_{j}$ в качестве своего соседа, если соседи были выбраны пропорционально их плотности вероятности при гауссовой функции с центром в $x_{i}$ ." ^{[ 2 ]}

Теперь определите

p_{ij}={\frac {p_{j\mid i}+p_{i\mid j}}{2N}}

Это мотивировано, потому что $p_{i}$ и $p_{j}$ из N выборок оцениваются как 1/N, поэтому условную вероятность можно записать как $p_{i\mid j}=Np_{ij}$ и $p_{j\mid i}=Np_{ji}$ . С $p_{ij}=p_{ji}$ , вы можете получить предыдущую формулу.

Также обратите внимание, что $p_{ii}=0$ и $\sum _{i,j}p_{ij}=1$ .

Пропускная способность гауссовых ядер $\sigma _{i}$ задается таким образом, чтобы энтропия условного распределения равнялась заранее определенной энтропии с использованием метода деления пополам . В результате полоса пропускания адаптируется к плотности данных: меньшие значения $\sigma _{i}$ используются в более плотных частях пространства данных.

Поскольку ядро Гаусса использует евклидово расстояние $\lVert x_{i}-x_{j}\rVert$ на него влияет проклятие размерности , а в многомерных данных, когда расстояния теряют способность различать, $p_{ij}$ станут слишком похожими (асимптотически они сходятся к константе). Чтобы облегчить эту проблему , было предложено скорректировать расстояния с помощью степенного преобразования на основе внутреннего размера каждой точки. ^{[ 12 ]}

t-SNE стремится изучить $d$ трехмерная карта $\mathbf {y} _{1},\dots ,\mathbf {y} _{N}$ (с $\mathbf {y} _{i}\in \mathbb {R} ^{d}$ и $d$ обычно выбирается как 2 или 3), что отражает сходство $p_{ij}$ как можно лучше. С этой целью он измеряет сходство $q_{ij}$ между двумя точками на карте $\mathbf {y} _{i}$ и $\mathbf {y} _{j}$ , используя очень похожий подход. В частности, для $i\neq j$ , определять $q_{ij}$ как

q_{ij}={\frac {(1+\lVert \mathbf {y} _{i}-\mathbf {y} _{j}\rVert ^{2})^{-1}}{\sum _{k}\sum _{l\neq k}(1+\lVert \mathbf {y} _{k}-\mathbf {y} _{l}\rVert ^{2})^{-1}}}

и установить $q_{ii}=0$ . с тяжелым хвостом Здесь t-распределение Стьюдента (с одной степенью свободы, которое совпадает с распределением Коши ) используется для измерения сходства между точками низкой размерности, чтобы позволить моделировать разнородные объекты далеко друг от друга на карте. .

Расположение точек $\mathbf {y} _{i}$ на карте определяются путем минимизации (несимметричного) расхождения Кульбака – Лейблера распределения $P$ из распределения $Q$ , то есть:

\mathrm {KL} \left(P\parallel Q\right)=\sum _{i\neq j}p_{ij}\log {\frac {p_{ij}}{q_{ij}}}

Минимизация расходимости Кульбака–Лейблера по точкам $\mathbf {y} _{i}$ выполняется с использованием градиентного спуска . Результатом этой оптимизации является карта, отражающая сходство между многомерными входными данными.

Выход

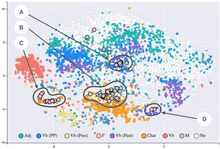
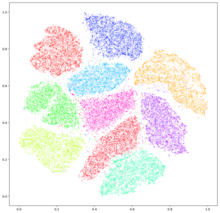
Хотя на графиках t-SNE часто отображаются кластеры , на визуальные кластеры может сильно влиять выбранная параметризация, поэтому необходимо хорошее понимание параметров t-SNE. Можно показать, что такие «кластеры» появляются даже в структурированных данных без четкой кластеризации. ^{[ 13 ]} и поэтому могут быть ложные выводы. Точно так же размер кластеров, создаваемых t-SNE, не информативен, как и расстояние между кластерами. ^{[ 14 ]} Таким образом, для выбора параметров и проверки результатов может потребоваться интерактивное исследование. ^{[ 15 ]}^{[ 16 ]} Было показано, что t-SNE часто может восстанавливать хорошо разделенные кластеры и при специальном выборе параметров аппроксимирует простую форму спектральной кластеризации . ^{[ 17 ]}

Программное обеспечение

Пакет R Rtsne t-SNE в R. реализует
ELKI содержит tSNE, также с приближением Барнса-Хата.
scikit-learn , популярная библиотека машинного обучения на Python, реализует t-SNE как с точными решениями, так и с приближением Барнса-Хата.
Tensorboard, комплект визуализации, связанный с TensorFlow , также реализует t-SNE ( онлайн-версия ).
Пакет Julia . TSne реализует t-SNE

Ссылки

^ Хинтон, Джеффри; Роуэйс, Сэм (январь 2002 г.). Встраивание стохастических соседей (PDF) . Нейронные системы обработки информации .
^ Перейти обратно: ^а ^б ван дер Маатен, LJP; Хинтон, GE (ноябрь 2008 г.). «Визуализация данных с использованием t-SNE» (PDF) . Журнал исследований машинного обучения . 9 : 2579–2605.
^ Гаши, И.; Станкович, В.; Лейта, К.; Тоннард, О. (2009). «Экспериментальное исследование разнообразия с помощью готовых антивирусных механизмов». Труды Международного симпозиума IEEE по сетевым вычислениям и приложениям : 4–11.
^ Хамель, П.; Эк, Д. (2010). «Особенности изучения музыкального аудио с помощью Deep Belief Networks». Материалы конференции Международного общества поиска музыкальной информации : 339–344.
^ Джеймисон, Арканзас; Гигер, ML; Друккер, К.; Луи, Х.; Юань, Ю.; Бхушан, Н. (2010). «Изучение уменьшения размеров нелинейного пространства объектов и представления данных в CADx груди с помощью лапласовых собственных карт и t-SNE» . Медицинская физика . 37 (1): 339–351. дои : 10.1118/1.3267037 . ПМК 2807447 . ПМИД 20175497 .
^ Уоллах, И.; Лилиан, Р. (2009). «База данных о белках-малых молекулах, неизбыточный структурный ресурс для анализа связывания белка с лигандом» . Биоинформатика . 25 (5): 615–620. doi : 10.1093/биоинформатика/btp035 . ПМИД 19153135 .
^ Баламурали, Мехала; Сильверсайдс, Кэтрин Л.; Мелкумян, Арман (01.04.2019). «Сравнение t-SNE, SOM и SPADE для определения областей типов материалов в геологических данных» . Компьютеры и геонауки . 125 : 78–89. Бибкод : 2019CG....125...78B . дои : 10.1016/j.cageo.2019.01.011 . ISSN 0098-3004 . S2CID 67926902 .
^ Баламурали, Мехала; Мелкумян, Арман (2016). Хиросе, Акира; Одзава, Сейичи; Дойя, Кенджи; Икеда, Казуси; Ли, Минхо; Лю, Деронг (ред.). «Визуализация и кластеризация геологической области на основе t-SNE» . Нейронная обработка информации . Конспекты лекций по информатике. 9950 . Чам: Springer International Publishing: 565–572. дои : 10.1007/978-3-319-46681-1_67 . ISBN 978-3-319-46681-1 .
^ Люнг, Раймонд; Баламурали, Мехала; Мелкумян, Арман (01.01.2021). «Примеры стратегий усечения выборки для удаления выбросов в геохимических данных: подход устойчивого расстояния MCD в сравнении с кластеризацией ансамбля t-SNE» . Математические науки о Земле . 53 (1): 105–130. Бибкод : 2021MaGeo..53..105L . дои : 10.1007/s11004-019-09839-z . ISSN 1874-8953 . S2CID 208329378 .
^ Бирджандталаб, Дж.; Пуян, МБ; Нурани, М. (01 февраля 2016 г.). «Нелинейное уменьшение размеров для обнаружения эпилептических припадков на основе ЭЭГ». Международная конференция IEEE-EMBS по биомедицинской и медицинской информатике (BHI) , 2016 г. стр. 595–598. дои : 10.1109/BHI.2016.7455968 . ISBN 978-1-5090-2455-1 . S2CID 8074617 .
^ Пеццотти, Никола. «Приближенный и управляемый пользователем tSNE для прогрессивной визуальной аналитики» (PDF) . Проверено 31 августа 2023 г.
^ Шуберт, Эрих; Герц, Майкл (04 октября 2017 г.). Внутреннее t-стохастическое встраивание соседей для визуализации и обнаружения выбросов . SISAP 2017 – 10-я Международная конференция по поиску и применению сходства. стр. 188–203. дои : 10.1007/978-3-319-68474-1_13 .
^ «К-означает кластеризацию на выходе t-SNE» . Крест проверен . Проверено 16 апреля 2018 г.
^ Ваттенберг, Мартин; Вьегас, Фернанда; Джонсон, Ян (13 октября 2016 г.). «Как эффективно использовать t-SNE» . Дистиллировать . 1 (10): е2. дои : 10.23915/distill.00002 . ISSN 2476-0757 .
^ Пеццотти, Никола; Лелиевельдт, Будевейн П.Ф.; Маатен, Лоренс ван дер; Холлт, Томас; Эйземанн, Эльмар; Виланова, Анна (01.07.2017). «Приблизительный и управляемый пользователем tSNE для прогрессивной визуальной аналитики» Транзакции IEEE по визуализации и компьютерной графике . 23 (7): 1739–1752. arXiv : 1512.01655 . дои : 10.1109/tvcg.2016.2570755 . ISSN 1077-2626 . ПМИД 28113434 . S2CID 353336 .
^ Ваттенберг, Мартин; Вьегас, Фернанда; Джонсон, Ян (13 октября 2016 г.). «Как эффективно использовать t-SNE» . Дистиллировать . 1 (10). дои : 10.23915/distill.00002 . Проверено 4 декабря 2017 г.
^ Линдерман, Джордж К.; Штайнербергер, Стефан (8 июня 2017 г.). «Кластеризация с t-SNE, доказуемо». arXiv : 1706.02582 [ cs.LG ].

Внешние ссылки

Визуализация данных с помощью t-SNE , Google Tech Talk о t-SNE
Реализации t-SNE на разных языках . Коллекция ссылок поддерживается Лоренсом ван дер Маатеном.

[SNE-1] Хинтон, Джеффри; Роуэйс, Сэм (январь 2002 г.). Встраивание стохастических соседей (PDF) . Нейронные системы обработки информации .

[MaatenHinton-2] Перейти обратно: ^а ^б ван дер Маатен, LJP; Хинтон, GE (ноябрь 2008 г.). «Визуализация данных с использованием t-SNE» (PDF) . Журнал исследований машинного обучения . 9 : 2579–2605.

[3] Гаши, И.; Станкович, В.; Лейта, К.; Тоннард, О. (2009). «Экспериментальное исследование разнообразия с помощью готовых антивирусных механизмов». Труды Международного симпозиума IEEE по сетевым вычислениям и приложениям : 4–11.

[4] Хамель, П.; Эк, Д. (2010). «Особенности изучения музыкального аудио с помощью Deep Belief Networks». Материалы конференции Международного общества поиска музыкальной информации : 339–344.

[5] Джеймисон, Арканзас; Гигер, ML; Друккер, К.; Луи, Х.; Юань, Ю.; Бхушан, Н. (2010). «Изучение уменьшения размеров нелинейного пространства объектов и представления данных в CADx груди с помощью лапласовых собственных карт и t-SNE» . Медицинская физика . 37 (1): 339–351. дои : 10.1118/1.3267037 . ПМК 2807447 . ПМИД 20175497 .

[6] Уоллах, И.; Лилиан, Р. (2009). «База данных о белках-малых молекулах, неизбыточный структурный ресурс для анализа связывания белка с лигандом» . Биоинформатика . 25 (5): 615–620. doi : 10.1093/биоинформатика/btp035 . ПМИД 19153135 .

[7] Баламурали, Мехала; Сильверсайдс, Кэтрин Л.; Мелкумян, Арман (01.04.2019). «Сравнение t-SNE, SOM и SPADE для определения областей типов материалов в геологических данных» . Компьютеры и геонауки . 125 : 78–89. Бибкод : 2019CG....125...78B . дои : 10.1016/j.cageo.2019.01.011 . ISSN 0098-3004 . S2CID 67926902 .

[8] Баламурали, Мехала; Мелкумян, Арман (2016). Хиросе, Акира; Одзава, Сейичи; Дойя, Кенджи; Икеда, Казуси; Ли, Минхо; Лю, Деронг (ред.). «Визуализация и кластеризация геологической области на основе t-SNE» . Нейронная обработка информации . Конспекты лекций по информатике. 9950 . Чам: Springer International Publishing: 565–572. дои : 10.1007/978-3-319-46681-1_67 . ISBN 978-3-319-46681-1 .

[9] Люнг, Раймонд; Баламурали, Мехала; Мелкумян, Арман (01.01.2021). «Примеры стратегий усечения выборки для удаления выбросов в геохимических данных: подход устойчивого расстояния MCD в сравнении с кластеризацией ансамбля t-SNE» . Математические науки о Земле . 53 (1): 105–130. Бибкод : 2021MaGeo..53..105L . дои : 10.1007/s11004-019-09839-z . ISSN 1874-8953 . S2CID 208329378 .

[10] Бирджандталаб, Дж.; Пуян, МБ; Нурани, М. (01 февраля 2016 г.). «Нелинейное уменьшение размеров для обнаружения эпилептических припадков на основе ЭЭГ». Международная конференция IEEE-EMBS по биомедицинской и медицинской информатике (BHI) , 2016 г. стр. 595–598. дои : 10.1109/BHI.2016.7455968 . ISBN 978-1-5090-2455-1 . S2CID 8074617 .

[11] Пеццотти, Никола. «Приближенный и управляемый пользователем tSNE для прогрессивной визуальной аналитики» (PDF) . Проверено 31 августа 2023 г.

[12] Шуберт, Эрих; Герц, Майкл (04 октября 2017 г.). Внутреннее t-стохастическое встраивание соседей для визуализации и обнаружения выбросов . SISAP 2017 – 10-я Международная конференция по поиску и применению сходства. стр. 188–203. дои : 10.1007/978-3-319-68474-1_13 .

[13] «К-означает кластеризацию на выходе t-SNE» . Крест проверен . Проверено 16 апреля 2018 г.

[14] Ваттенберг, Мартин; Вьегас, Фернанда; Джонсон, Ян (13 октября 2016 г.). «Как эффективно использовать t-SNE» . Дистиллировать . 1 (10): е2. дои : 10.23915/distill.00002 . ISSN 2476-0757 .

[15] Пеццотти, Никола; Лелиевельдт, Будевейн П.Ф.; Маатен, Лоренс ван дер; Холлт, Томас; Эйземанн, Эльмар; Виланова, Анна (01.07.2017). «Приблизительный и управляемый пользователем tSNE для прогрессивной визуальной аналитики» Транзакции IEEE по визуализации и компьютерной графике . 23 (7): 1739–1752. arXiv : 1512.01655 . дои : 10.1109/tvcg.2016.2570755 . ISSN 1077-2626 . ПМИД 28113434 . S2CID 353336 .

[16] Ваттенберг, Мартин; Вьегас, Фернанда; Джонсон, Ян (13 октября 2016 г.). «Как эффективно использовать t-SNE» . Дистиллировать . 1 (10). дои : 10.23915/distill.00002 . Проверено 4 декабря 2017 г.

[17] Линдерман, Джордж К.; Штайнербергер, Стефан (8 июня 2017 г.). «Кластеризация с t-SNE, доказуемо». arXiv : 1706.02582 [ cs.LG ].

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]