Сложная случайная величина

В теории вероятностей статистике комплексные и случайные величины представляют собой обобщение действительных случайных величин на комплексные числа , то есть возможные значения, которые может принимать комплексная случайная величина, являются комплексными числами. ^[1] Комплексные случайные величины всегда можно рассматривать как пары действительных случайных величин: их действительную и мнимую части. Следовательно, распределение одной комплексной случайной величины можно интерпретировать как совместное распределение двух действительных случайных величин.

Некоторые концепции реальных случайных величин имеют прямое обобщение на сложные случайные величины, например, определение среднего значения сложной случайной величины. Другие концепции уникальны для сложных случайных величин.

Приложения сложных случайных величин можно найти в цифровой обработке сигналов . ^[2] квадратурная амплитудная модуляция и теория информации .

Определение

Сложная случайная величина $Z$ в вероятностном пространстве $(\Omega ,{\mathcal {F}},P)$ это функция $Z\colon \Omega \rightarrow \mathbb {C}$ такая, что обе ее действительные части $\Re {(Z)}$ и его мнимая часть $\Im {(Z)}$ являются действительными случайными величинами на $(\Omega ,{\mathcal {F}},P)$ .

Примеры

Простой пример

Рассмотрим случайную величину, которая может принимать только три комплексных значения. $1+i,1-i,2$ с вероятностями, указанными в таблице. Это простой пример сложной случайной величины.

Вероятность $P(z)$	Ценить $z$
${\frac {1}{4}}$	$1+i$
${\frac {1}{4}}$	$1-i$
${\frac {1}{2}}$	$2$

Математическое ожидание этой случайной величины можно просто вычислить: $\operatorname {E} [Z]={\frac {1}{4}}(1+i)+{\frac {1}{4}}(1-i)+{\frac {1}{2}}2={\frac {3}{2}}.$

Равномерное распределение

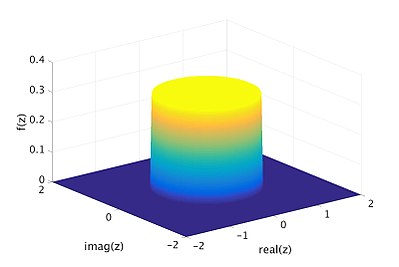
Другим примером сложной случайной величины является равномерное распределение по заполненному единичному кругу, т.е. множество $\{z\in \mathbb {C} \mid |z|\leq 1\}$ . Эта случайная величина является примером сложной случайной величины, для которой функция плотности вероятности определена . Функция плотности показана желтым диском и темно-синим основанием на следующем рисунке.

Комплексное нормальное распределение

В приложениях часто встречаются сложные гауссовы случайные величины. Они представляют собой прямое обобщение реальных гауссовских случайных величин. На следующем графике показан пример распределения такой переменной.

Кумулятивная функция распределения

Обобщение кумулятивной функции распределения от вещественных случайных величин к комплексным неочевидно, поскольку выражения вида $P(Z\leq 1+3i)$ не имеет смысла. Однако выражения вида $P(\Re {(Z)}\leq 1,\Im {(Z)}\leq 3)$ имеет смысл. Поэтому мы определяем кумулятивное распределение $F_{Z}:\mathbb {C} \to [0,1]$ сложных случайных величин через совместное распределение их вещественной и мнимой частей:

F_{Z}(z)=F_{\Re {(Z)},\Im {(Z)}}(\Re {(z)},\Im {(z)})=P(\Re {(Z)}\leq \Re {(z)},\Im {(Z)}\leq \Im {(z)})

( Уравнение 1 )

Функция плотности вероятности

Функция плотности вероятности комплексной случайной величины определяется как $f_{Z}(z)=f_{\Re {(Z)},\Im {(Z)}}(\Re {(z)},\Im {(z)})$ , т.е. значение функции плотности в точке $z\in \mathbb {C}$ определяется равным значению совместной плотности действительной и мнимой частей случайной величины, оцененной в точке $(\Re {(z)},\Im {(z)})$ .

Эквивалентное определение дается формулой $f_{Z}(z)={\frac {\partial ^{2}}{\partial x\partial y}}P(\Re {(Z)}\leq x,\Im {(Z)}\leq y)$ где $x=\Re {(z)}$ и $y=\Im {(z)}$ .

Как и в реальном случае, функция плотности может не существовать.

Ожидание

Ожидание сложной случайной величины определяется на основе определения ожидания реальной случайной величины: ^[3]^{: с. 112}

\operatorname {E} [Z]=\operatorname {E} [\Re {(Z)}]+i\operatorname {E} [\Im {(Z)}]

( Уравнение 2 )

Обратите внимание, что математическое ожидание сложной случайной величины не существует, если $\operatorname {E} [\Re {(Z)}]$ или $\operatorname {E} [\Im {(Z)}]$ не существует.

Если комплексная случайная величина $Z$ имеет функцию плотности вероятности $f_{Z}(z)$ , то математическое ожидание определяется выражением $\operatorname {E} [Z]=\iint _{\mathbb {C} }z\cdot f_{Z}(z)\,dx\,dy$ .

Если комплексная случайная величина $Z$ имеет функцию массы вероятности $p_{Z}(z)$ , то математическое ожидание определяется выражением $\operatorname {E} [Z]=\sum _{z\in \mathbb {Z} }z\cdot p_{Z}(z)$ .

Характеристики

Всякий раз, когда существует математическое ожидание сложной случайной величины, математическое ожидание и комплексное сопряжение коммутируют:

{\overline {\operatorname {E} [Z]}}=\operatorname {E} [{\overline {Z}}].

Оператор ожидаемого значения $\operatorname {E} [\cdot ]$ является линейным в том смысле, что

\operatorname {E} [aZ+bW]=a\operatorname {E} [Z]+b\operatorname {E} [W]

для любых комплексных коэффициентов $a,b$ даже если $Z$ и $W$ не являются независимыми .

Дисперсия и псевдодисперсия

Дисперсия определяется в абсолютных квадратах как: ^[3]^: 117

\operatorname {K} _{ZZ}=\operatorname {Var} [Z]=\operatorname {E} \left[\left|Z-\operatorname {E} [Z]\right|^{2}\right]=\operatorname {E} [|Z|^{2}]-\left|\operatorname {E} [Z]\right|^{2}

( Уравнение 3 )

Характеристики

Дисперсия всегда является неотрицательным действительным числом. Он равен сумме дисперсий действительной и мнимой частей комплексной случайной величины:

\operatorname {Var} [Z]=\operatorname {Var} [\Re {(Z)}]+\operatorname {Var} [\Im {(Z)}].

Дисперсия линейной комбинации сложных случайных величин может быть рассчитана по следующей формуле:

\operatorname {Var} \left[\sum _{k=1}^{N}a_{k}Z_{k}\right]=\sum _{i=1}^{N}\sum _{j=1}^{N}a_{i}{\overline {a_{j}}}\operatorname {Cov} [Z_{i},Z_{j}].

Псевдовариантность

Псевдодисперсия комплексных является частным случаем псевдоковариации и определяется в терминах обычных квадратов , определяемых следующим образом:

\operatorname {J} _{ZZ}=\operatorname {E} [(Z-\operatorname {E} [Z])^{2}]=\operatorname {E} [Z^{2}]-(\operatorname {E} [Z])^{2}

( Уравнение 4 )

В отличие от дисперсии $Z$ , которая всегда действительна и положительна, псевдодисперсия $Z$ вообще сложный.

Ковариационная матрица действительных и мнимых частей

Для общей комплексной случайной величины пара $(\Re {(Z)},\Im {(Z)})$ имеет ковариационную матрицу вида:

{\begin{bmatrix}\operatorname {Var} [\Re {(Z)}]&\operatorname {Cov} [\Im {(Z)},\Re {(Z)}]\\\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]&\operatorname {Var} [\Im {(Z)}]\end{bmatrix}}

Матрица симметрична, поэтому $\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]=\operatorname {Cov} [\Im {(Z)},\Re {(Z)}]$

Его элементы равны:

{\begin{aligned}&\operatorname {Var} [\Re {(Z)}]={\tfrac {1}{2}}\operatorname {Re} (\operatorname {K} _{ZZ}+\operatorname {J} _{ZZ})\\&\operatorname {Var} [\Im {(Z)}]={\tfrac {1}{2}}\operatorname {Re} (\operatorname {K} _{ZZ}-\operatorname {J} _{ZZ})\\&\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]={\tfrac {1}{2}}\operatorname {Im} (\operatorname {J} _{ZZ})\\\end{aligned}}

Наоборот:

{\begin{aligned}&\operatorname {K} _{ZZ}=\operatorname {Var} [\Re {(Z)}]+\operatorname {Var} [\Im {(Z)}]\\&\operatorname {J} _{ZZ}=\operatorname {Var} [\Re {(Z)}]-\operatorname {Var} [\Im {(Z)}]+i2\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]\end{aligned}}

Ковариация и псевдоковариация

Ковариация величинами между двумя комплексными случайными $Z,W$ определяется как ^[3]^: 119

\operatorname {K} _{ZW}=\operatorname {Cov} [Z,W]=\operatorname {E} [(Z-\operatorname {E} [Z]){\overline {(W-\operatorname {E} [W])}}]=\operatorname {E} [Z{\overline {W}}]-\operatorname {E} [Z]\operatorname {E} [{\overline {W}}]

( Уравнение 5 )

Обратите внимание на комплексное сопряжение второго фактора в определении.

В отличие от реальных случайных величин, мы также определяем псевдоковариацию (также называемую дополнительной дисперсией ):

\operatorname {J} _{ZW}=\operatorname {Cov} [Z,{\overline {W}}]=\operatorname {E} [(Z-\operatorname {E} [Z])(W-\operatorname {E} [W])]=\operatorname {E} [ZW]-\operatorname {E} [Z]\operatorname {E} [W]

( Уравнение 6 )

Статистика второго порядка полностью характеризуется ковариацией и псевдоковариацией.

Характеристики

Ковариация обладает следующими свойствами:

$\operatorname {Cov} [Z,W]={\overline {\operatorname {Cov} [W,Z]}}$ (Сопряженная симметрия)
$\operatorname {Cov} [\alpha Z,W]=\alpha \operatorname {Cov} [Z,W]$ (полуторалинейность)
$\operatorname {Cov} [Z,\alpha W]={\overline {\alpha }}\operatorname {Cov} [Z,W]$
$\operatorname {Cov} [Z_{1}+Z_{2},W]=\operatorname {Cov} [Z_{1},W]+\operatorname {Cov} [Z_{2},W]$
$\operatorname {Cov} [Z,W_{1}+W_{2}]=\operatorname {Cov} [Z,W_{1}]+\operatorname {Cov} [Z,W_{2}]$
$\operatorname {Cov} [Z,Z]={\operatorname {Var} [Z]}$
Некоррелированность: две сложные случайные величины $Z$ и $W$ называются некоррелированными, если $\operatorname {K} _{ZW}=\operatorname {J} _{ZW}=0$ (см. также: некоррелированность (теория вероятностей) ).
Ортогональность: две комплексные случайные величины $Z$ и $W$ называются ортогональными, если $\operatorname {E} [Z{\overline {W}}]=0$ .

Круговая симметрия

Круговая симметрия сложных случайных величин является распространенным предположением, используемым в области беспроводной связи. Типичным примером круговой симметричной комплексной случайной величины является комплексная гауссова случайная величина с нулевым средним и нулевой псевдоковариационной матрицей.

Сложная случайная величина $Z$ является кругосимметричным, если для любого детерминированного $\phi \in [-\pi ,\pi ]$ , распределение $e^{\mathrm {i} \phi }Z$ равно распределению $Z$ .

Характеристики

По определению, циклически симметричная комплексная случайная величина имеет $\operatorname {E} [Z]=\operatorname {E} [e^{\mathrm {i} \phi }Z]=e^{\mathrm {i} \phi }\operatorname {E} [Z]$ для любого $\phi$ .

Таким образом, математическое ожидание циклически симметричной комплексной случайной величины может быть только нулевым или неопределенным.

Кроме того, $\operatorname {E} [ZZ]=\operatorname {E} [e^{\mathrm {i} \phi }Ze^{\mathrm {i} \phi }Z]=e^{\mathrm {2} i\phi }\operatorname {E} [ZZ]$ для любого $\phi$ .

Таким образом, псевдодисперсия циклически симметричной комплексной случайной величины может быть только нулевой.

Если $Z$ и $e^{\mathrm {i} \phi }Z$ имеют одинаковое распределение, фаза $Z$ должны быть равномерно распределены по $[-\pi ,\pi ]$ и не зависит от амплитуды $Z$ . ^[4]

Правильные комплексные случайные величины

Понятие собственных случайных величин уникально для комплексных случайных величин и не имеет соответствующего понятия для реальных случайных величин.

Сложная случайная величина $Z$ называется правильным, если выполняются все три условия:

$\operatorname {E} [Z]=0$
$\operatorname {Var} [Z]<\infty$
$\operatorname {E} [Z^{2}]=0$

Это определение эквивалентно следующим условиям. Это означает, что комплексная случайная величина является правильной тогда и только тогда, когда:

$\operatorname {E} [Z]=0$
$\operatorname {E} [\Re {(Z)}^{2}]=\operatorname {E} [\Im {(Z)}^{2}]\neq \infty$
$\operatorname {E} [\Re {(Z)}\Im {(Z)}]=0$

Теорема . Любая циклически симметричная комплексная случайная величина с конечной дисперсией является собственной.

Для правильной комплексной случайной величины ковариационная матрица пары $(\Re {(Z)},\Im {(Z)})$ имеет следующую простую форму:

{\begin{bmatrix}{\frac {1}{2}}\operatorname {Var} [Z]&0\\0&{\frac {1}{2}}\operatorname {Var} [Z]\end{bmatrix}}

.

Т.е.:

{\begin{aligned}&\operatorname {Var} [\Re {(Z)}]=\operatorname {Var} [\Im {(Z)}]={\tfrac {1}{2}}\operatorname {Var} [Z]\\&\operatorname {Cov} [\Re {(Z)},\Im {(Z)}]=0\\\end{aligned}}

Неравенство Коши-Шварца

Неравенство Коши -Шварца для комплексных случайных величин, которое можно вывести с помощью неравенства треугольника и неравенства Гёльдера , равно

\left|\operatorname {E} \left[Z{\overline {W}}\right]\right|^{2}\leq \left|\operatorname {E} \left[\left|Z{\overline {W}}\right|\right]\right|^{2}\leq \operatorname {E} \left[|Z|^{2}\right]\operatorname {E} \left[|W|^{2}\right]

.

Характеристическая функция

Характеристической функцией комплексной случайной величины является функция $\mathbb {C} \to \mathbb {C}$ определяется

\varphi _{Z}(\omega )=\operatorname {E} \left[e^{i\Re {({\overline {\omega }}Z)}}\right]=\operatorname {E} \left[e^{i(\Re {(\omega )}\Re {(Z)}+\Im {(\omega )}\Im {(Z)})}\right].

См. также

Ссылки

^ Эрикссон, Ян; Оллила, Эса; Койвунен, Виза (2009). Еще раз о статистике сложных случайных величин . Международная конференция IEEE 2009 г. по акустике, речи и обработке сигналов. Тайбэй, Тайвань: Институт инженеров по электротехнике и электронике . стр. 3565–3568. дои : 10.1109/ICASSP.2009.4960396 .
^ Лапидот, А. (2009). Фонд цифровых коммуникаций . Издательство Кембриджского университета. ISBN 9780521193955 .
^ Jump up to: ^а ^б ^с Пак, Кун Иль (2018). Основы теории вероятности и случайных процессов с приложениями к средствам связи . Спрингер. ISBN 978-3-319-68074-3 .
^ Питер Дж. Шрайер, Луи Л. Шарф (2011). Статистическая обработка сигналов комплексных данных . Издательство Кембриджского университета. ISBN 9780511815911 .

[1] Эрикссон, Ян; Оллила, Эса; Койвунен, Виза (2009). Еще раз о статистике сложных случайных величин . Международная конференция IEEE 2009 г. по акустике, речи и обработке сигналов. Тайбэй, Тайвань: Институт инженеров по электротехнике и электронике . стр. 3565–3568. дои : 10.1109/ICASSP.2009.4960396 .

[2] Лапидот, А. (2009). Фонд цифровых коммуникаций . Издательство Кембриджского университета. ISBN 9780521193955 .

[KunIlPark-3] Jump up to: ^а ^б ^с Пак, Кун Иль (2018). Основы теории вероятности и случайных процессов с приложениями к средствам связи . Спрингер. ISBN 978-3-319-68074-3 .

[4] Питер Дж. Шрайер, Луи Л. Шарф (2011). Статистическая обработка сигналов комплексных данных . Издательство Кембриджского университета. ISBN 9780511815911 .

[1]

[2]

[3]

[4]