Радиус схождения
В математике радиус сходимости степенного ряда — это радиус наибольшего круга в центре ряда, в котором этот ряд сходится . Это либо неотрицательное действительное число, либо . Когда он положителен, степенной ряд сходится абсолютно и равномерно на компактах внутри открытого диска радиуса, равного радиусу сходимости, и является рядом Тейлора аналитической функции , к которой он сходится. В случае множественных особенностей функции (особенностями являются те значения аргумента, для которых функция не определена), радиус сходимости является кратчайшим или минимальным из всех соответствующих расстояний (которые все являются неотрицательными числами), рассчитанных по формуле центр круга сходимости к соответствующим особенностям функции.
Определение
[ редактировать ]Для степенного ряда f, определяемого как:
где
- а — комплексная константа, центр круга сходимости ,
- c n - n -й комплексный коэффициент, и
- z — комплексная переменная.
Радиус сходимости r представляет собой неотрицательное действительное число или такая, что ряд сходится, если
и расходится, если
Некоторые могут предпочесть альтернативное определение, поскольку существование очевидно:
На границе, т. е. там, где | г - а | = r поведение степенного ряда может быть сложным: ряд может сходиться для одних значений z и расходиться для других. Радиус сходимости бесконечен, если ряд сходится для всех комплексных чисел z . [1]
Нахождение радиуса сходимости
[ редактировать ]Возникают два случая:
- Первый случай теоретический: когда известны все коэффициенты затем вы берете определенные пределы и находите точный радиус сходимости.
- Второй случай практичен: когда вы строите решение сложной задачи с помощью степенного ряда, вы обычно знаете только конечное число членов степенного ряда, от пары до ста членов. Во втором случае экстраполяция графика оценивает радиус сходимости.
Теоретический радиус
[ редактировать ]Радиус сходимости можно найти, применив корневой тест к членам ряда. Корневой тест использует число
«lim sup» означает верхний предел . Корневой тест утверждает, что ряд сходится, если C <1, и расходится, если C > 1. Отсюда следует, что степенной ряд сходится, если расстояние от z до центра a меньше, чем
и расходится, если расстояние превышает это число; это утверждение представляет собой теорему Коши–Адамара . Обратите внимание, что r = 1/0 интерпретируется как бесконечный радиус, а это означает, что f — целая функция .
Предел, используемый в тесте отношения, обычно легче вычислить, и когда этот предел существует, это показывает, что радиус сходимости конечен.
Это показано следующим образом. Тест на соотношение говорит, что ряд сходится, если
Это эквивалентно
Практическая оценка радиуса в случае реальных коэффициентов
[ редактировать ]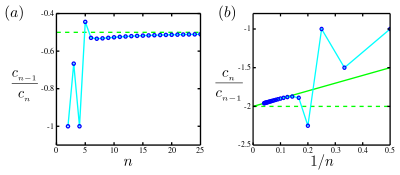
Сплошная зеленая линия представляет собой прямую асимптоту на графике Домба – Сайкса, [2] график (b), который пересекает вертикальную ось в точке -2 и имеет наклон +1. Таким образом, имеется сингулярность в и поэтому радиус сходимости равен
Обычно в научных приложениях используется только конечное число коэффициентов. известны. Обычно, как увеличивается, эти коэффициенты приобретают регулярное поведение, определяемое ближайшей особенностью, ограничивающей радиус. В этом случае были разработаны два основных метода, основанные на том факте, что коэффициенты ряда Тейлора примерно экспоненциальны с отношением где r — радиус сходимости.
- Основной случай - это когда коэффициенты в конечном итоге имеют общий знак или чередуются по знаку. Как указывалось ранее в статье, во многих случаях предел существует, и в этом случае . Отрицательный означает, что особенность, ограничивающая сходимость, находится на отрицательной оси. Оцените этот предел, построив график против и графически экстраполируем на (эффективно ) посредством линейной подгонки. Перехват с оценивает обратную величину радиуса сходимости, . Этот график называется графиком Домба-Сайкса . [3]
- Более сложный случай — когда знаки коэффициентов имеют более сложную картину. Мерсер и Робертс предложили следующую процедуру. [4] Определите связанную последовательность Постройте конечное число известных против и графически экстраполируем на посредством линейной подгонки. Перехват с оценивает обратную величину радиуса сходимости, . Эта процедура также оценивает две другие характеристики предельной особенности сходимости. Предположим, что ближайшая особенность имеет степень и имеет угол к реальной оси. Тогда наклон линейной аппроксимации, указанный выше, равен . Далее, сюжет против , затем линейная аппроксимация экстраполируется на имеет перехват в .
Радиус сходимости в комплексном анализе
[ редактировать ]Степенной ряд с положительным радиусом сходимости можно превратить в голоморфную функцию , приняв в качестве ее аргумента комплексную переменную. Радиус сходимости можно охарактеризовать следующей теоремой:
- Радиус сходимости степенного ряда f с центром в точке a равен расстоянию от a до ближайшей точки, где f не может быть определена способом, делающим его голоморфным.
Совокупность всех точек, расстояние до которых строго меньше радиуса сходимости, называется диском сходимости .

Ближайшая точка означает ближайшую точку на комплексной плоскости , не обязательно на действительной прямой, даже если центр и все коэффициенты вещественные. Например, функция
не имеет особенностей на действительной прямой, так как не имеет реальных корней. Его ряд Тейлора около 0 имеет вид
Корневой тест показывает, что ее радиус сходимости равен 1. В соответствии с этим функция f ( z ) имеет особенности при ± i , которые находятся на расстоянии 1 от 0.
Доказательство этой теоремы см. в аналитичности голоморфных функций .
Простой пример
[ редактировать ]Арктангенс тригонометрии можно разложить в степенной ряд:
В этом случае легко применить корневой тест и найти, что радиус сходимости равен 1.
Более сложный пример
[ редактировать ]Рассмотрим этот степенной ряд:
где рациональные числа B n являются числами Бернулли . Может быть затруднительно попытаться применить критерий отношения, чтобы найти радиус сходимости этого ряда. Но изложенная выше теорема комплексного анализа быстро решает проблему. При z = 0 особенности фактически нет, поскольку особенность устранима . Таким образом, единственные неустранимые особенности расположены в других точках, где знаменатель равен нулю. Мы решаем
напомнив, что если z = x + iy и e запах = cos( y ) + я sin( y ) тогда
а затем примем x и y за реальные. Поскольку y действительно, абсолютное значение cos( y ) + i sin( y ) обязательно равно 1. Следовательно, абсолютное значение e С может быть 1, только если e х равен 1; поскольку x действителен, это происходит только в том случае, если x = 0. Следовательно, z чисто мнимый и cos( y ) + i sin( y ) = 1 . Поскольку y вещественный, это происходит только в том случае, если cos( y ) = 1 и sin( y ) = 0, так что y является целым числом, кратным 2 π . Следовательно, особые точки этой функции возникают при
- z = ненулевое целое число, кратное 2 π i .
Ближайшие к 0 особенности, которые являются центром разложения в степенной ряд, находятся в пределах ±2 π i . Расстояние от центра до любой из этих точек составляет 2 π , поэтому радиус сходимости равен 2 π .
Схождение на границе
[ редактировать ]Если степенной ряд разложен вокруг точки a и радиус сходимости равен r , то множество всех точек z таких, что | г - а | = r — окружность , называемая границей диска сходимости. Степенной ряд может расходиться в каждой точке границы, расходиться в некоторых точках и сходиться в других точках или сходиться во всех точках границы. Более того, даже если ряд сходится всюду на границе (даже равномерно), он не обязательно сходится абсолютно.
Пример 1: Степенной ряд для функции f ( z ) = 1/(1 − z ) , развернутый вокруг z = 0 , что просто
имеет радиус сходимости 1 и расходится в каждой точке границы.
Пример 2: Степенной ряд для g ( z ) = −ln(1 − z ) , расширенный вокруг z = 0 , что равно
имеет радиус сходимости 1 и расходится при z = 1, но сходится во всех остальных точках границы. Функция f ( z ) из примера 1 является производной от g ( z ) .
Пример 3: Степенной ряд
имеет радиус сходимости 1 и сходится всюду на границе абсолютно. Если h — функция, представленная этим рядом на единичном круге, то производная h ( z ) равна g ( z )/ z с g из примера 2. Оказывается, что h ( z ) — это функция дилогарифма .
Пример 4: Степенной ряд
имеет радиус сходимости 1 и сходится равномерно на всей границе | г | = 1 , но не сходится абсолютно на границе. [5]
Скорость сходимости
[ редактировать ]Если расширить функцию
вокруг точки x = 0, находим, что радиус сходимости этого ряда равен это означает, что этот ряд сходится для всех комплексных чисел. Однако в приложениях часто интересует точность числового ответа . На точность ответа влияет как количество членов, так и значение, по которому следует оценивать ряд. Например, если мы хотим вычислить sin(0,1) с точностью до пяти знаков после запятой, нам нужны только первые два члена ряда. Однако, если нам нужна такая же точность для x = 1, мы должны вычислить и просуммировать первые пять членов ряда. Для sin(10) требуются первые 18 членов ряда, а для sin(100) нам нужно вычислить первые 141 член.
Таким образом, для этих конкретных значений самая быстрая сходимость разложения степенного ряда происходит в центре, и по мере удаления от центра сходимости скорость сходимости замедляется, пока вы не достигнете границы (если она существует) и не пересечете ее, в в этом случае ряд расходится.
Абсцисса сходимости ряда Дирихле
[ редактировать ]Аналогичным понятием является абсцисса сходимости ряда Дирихле.
Такой ряд сходится, если действительная часть s больше определенного числа, зависящего от коэффициентов a n : абсциссы сходимости.
Примечания
[ редактировать ]- ^ Математический анализ-II . Кришна Пракашан Медиа. 16 ноября 2010 г.
- ^ См. Рисунок 8.1 в: Хинч, Э.Дж. (1991), Методы возмущений , Кембриджские тексты по прикладной математике, том. 6, Издательство Кембриджского университета, с. 146, ISBN 0-521-37897-4
- ^ Домб, К.; Сайкс, М.Ф. (1957), «О восприимчивости ферромагнетиков выше точки Кюри», Proc. Р. Сок. Лонд. A , 240 (1221): 214–228, Bibcode : 1957RSPSA.240..214D , doi : 10.1098/rspa.1957.0078 , S2CID 119974403
- ^ Мерсер, Дж.Н.; Робертс, AJ (1990), «Описание центрального многообразия дисперсии загрязнений в каналах с различными свойствами потока», SIAM J. Appl. Математика. , 50 (6): 1547–1565, doi : 10.1137/0150091
- ^ Серпинский, В. (1918). «О степенном ряде, который сходится равномерно, но не абсолютно на всем кругу сходимости» . Математические и физические работы . 29 (1): 263–266.
Ссылки
[ редактировать ]- Браун, Джеймс; Черчилль, Руэл (1989), Комплексные переменные и приложения , Нью-Йорк: McGraw-Hill , ISBN 978-0-07-010905-6
- Штейн, Элиас ; Шакарчи, Рами (2003), Комплексный анализ , Принстон, Нью-Джерси: Издательство Принстонского университета , ISBN 0-691-11385-8






![{\displaystyle C=\limsup _ {n\to \infty }{\sqrt[{n}]{|c_ {n}(za)^{n}|}} =\limsup _ {n\to \infty } \left({\sqrt[{n}]{|c_{n}|}}\right)|za|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67486298c59df5fc7583a5cc253024ebc9045ea)
![{\displaystyle r={\frac {1}{\limsup _{n\to \infty }{\sqrt[{n}]{|c_{n}|}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb0428211dc308307cbbd69ed6151785382c549b)





































