Распределение соотношения

Распределение отношений (также известное как распределение частных ) — это распределение вероятностей, построенное как распределение отношения случайных имеющих величин, два других известных распределения.Учитывая две (обычно независимые ) случайные величины X и Y , распределение случайной величины Z , которое формируется как отношение Z = X / Y, является распределением отношения .

Примером может служить распределение Коши (также называемое распределением нормального отношения ), которое представляет собой отношение двух нормально распределенных переменных с нулевым средним значением.Два других распределения, часто используемые в тестовой статистике, также являются распределениями отношений: t случайную величину с -распределение возникает из гауссовой случайной величины, разделенной на независимую распределением хи , в то время как F -распределение возникает из соотношения двух независимых распределенных по хи-квадрат случайных величин.В литературе рассматривались более общие распределения соотношений.

Часто распределения отношений имеют «тяжелый хвост» , и может быть сложно работать с такими распределениями и разрабатывать соответствующий статистический тест . метод, основанный на медиане . В качестве «обходного пути» был предложен

Алгебра случайных величин

Основная статья: Алгебра случайных величин

Отношение — это один из типов алгебры для случайных величин:С соотношением распределения связаны распределение продуктов , распределение сумм и распределение разностей . В более общем смысле можно говорить о комбинациях сумм, разностей, произведений и отношений.Многие из этих распределений описаны в книге Мелвина Д. Спрингера 1979 года «Алгебра случайных величин» .

Алгебраические правила, известные для обычных чисел, неприменимы к алгебре случайных величин.Например, если продукт C = AB и соотношение D = C/A, это не обязательно означает, что распределения D и B одинаковы. наблюдается своеобразный эффект Действительно, для распределения Коши : произведение и отношение двух независимых распределений Коши (с одинаковым параметром масштаба и параметром местоположения, установленным равным нулю) дадут одно и то же распределение. Это становится очевидным, если рассматривать распределение Коши как распределение отношений двух гауссовых распределений с нулевыми средними: рассмотрим две случайные величины Коши: $C_{1}$ и $C_{2}$ каждое построено на основе двух гауссовских распределений $C_{1}=G_{1}/G_{2}$ и $C_{2}=G_{3}/G_{4}$ затем

${\frac {C_{1}}{C_{2}}}={\frac {{G_{1}}/{G_{2}}}{{G_{3}}/{G_{4}}}}={\frac {G_{1}G_{4}}{G_{2}G_{3}}}={\frac {G_{1}}{G_{2}}}\times {\frac {G_{4}}{G_{3}}}=C_{1}\times C_{3},$

где $C_{3}=G_{4}/G_{3}$. Первый член представляет собой отношение двух распределений Коши, а последний член представляет собой произведение двух таких распределений.

Вывод

Способ получения соотношения распределения $Z=X/Y$ из совместного распределения двух других случайных величин X, Y , с совместным PDF-файлом $p_{X,Y}(x,y)$, представляет собой интегрирование следующей формы

$p_{Z}(z)=\int _{-\infty }^{+\infty }|y|\,p_{X,Y}(zy,y)\,dy.$

Если две переменные независимы, то $p_{XY}(x,y)=p_{X}(x)p_{Y}(y)$ и это становится

$p_{Z}(z)=\int _{-\infty }^{+\infty }|y|\,p_{X}(zy)p_{Y}(y)\,dy.$

Это может быть непросто. В качестве примера возьмем классическую задачу об отношении двух стандартных гауссовых выборок. Совместный PDF-файл

$p_{X,Y}(x,y)={\frac {1}{2\pi }}\exp \left(-{\frac {x^{2}}{2}}\right)\exp \left(-{\frac {y^{2}}{2}}\right)$

Определение $Z=X/Y$ у нас есть

${\begin{aligned}p_{Z}(z)&={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\,|y|\,\exp \left(-{\frac {\left(zy\right)^{2}}{2}}\right)\,\exp \left(-{\frac {y^{2}}{2}}\right)\,dy\\&={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\,|y|\,\exp \left(-{\frac {y^{2}\left(z^{2}+1\right)}{2}}\right)\,dy\end{aligned}}$

Используя известный определенный интеграл ${\textstyle \int _{0}^{\infty }\,x\,\exp \left(-cx^{2}\right)\,dx={\frac {1}{2c}}}$ мы получаем

$p_{Z}(z)={\frac {1}{\pi (z^{2}+1)}}$

распределение Стьюдента которое представляет собой распределение Коши или t- с n = 1

Преобразование Меллина также было предложено для получения распределений отношений.

В случае положительных независимых переменных поступают следующим образом. На диаграмме показано разделимое двумерное распределение. $f_{x,y}(x,y)=f_{x}(x)f_{y}(y)$ который имеет поддержку в положительном квадранте $x,y>0$ и мы хотим найти PDF-файл соотношения $R=X/Y$. Заштрихованный объем над линией $y=x/R$ представляет собой кумулятивное распределение функции $f_{x,y}(x,y)$ умноженное на логическую функцию $X/Y\leq R$. Плотность сначала интегрируется в горизонтальные полосы; горизонтальная полоса на высоте y простирается от x = 0 до x = Ry и имеет возрастающую вероятность ${\textstyle f_{y}(y)dy\int _{0}^{Ry}f_{x}(x)\,dx}$.
Во-вторых, интегрирование горизонтальных полос вверх по всем y дает объем вероятности над линией

$F_{R}(R)=\int _{0}^{\infty }f_{y}(y)\left(\int _{0}^{Ry}f_{x}(x)dx\right)dy$

Наконец, дифференцируйте $F_{R}(R)$ относительно $R$ чтобы получить PDF-файл $f_{R}(R)$.

$f_{R}(R)={\frac {d}{dR}}\left[\int _{0}^{\infty }f_{y}(y)\left(\int _{0}^{Ry}f_{x}(x)dx\right)dy\right]$

Переместим дифференцирование внутрь интеграла:

$f_{R}(R)=\int _{0}^{\infty }f_{y}(y)\left({\frac {d}{dR}}\int _{0}^{Ry}f_{x}(x)dx\right)dy$

и поскольку

${\frac {d}{dR}}\int _{0}^{Ry}f_{x}(x)dx=yf_{x}(Ry)$

затем

$f_{R}(R)=\int _{0}^{\infty }f_{y}(y)\;f_{x}(Ry)\;y\;dy$

В качестве примера найдите PDF-файл отношения R, когда

$f_{x}(x)=\alpha e^{-\alpha x},\;\;\;\;f_{y}(y)=\beta e^{-\beta y},\;\;\;x,y\geq 0$

Оценка совокупного распределения коэффициента

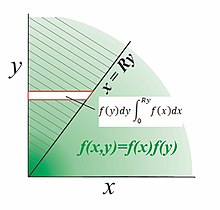
У нас есть

$\int _{0}^{Ry}f_{x}(x)dx=-e^{-\alpha x}\vert _{0}^{Ry}=1-e^{-\alpha Ry}$

таким образом

${\begin{aligned}F_{R}(R)&=\int _{0}^{\infty }f_{y}(y)\left(1-e^{-\alpha Ry}\right)dy=\int _{0}^{\infty }\beta e^{-\beta y}\left(1-e^{-\alpha Ry}\right)dy\\&=1-{\frac {\alpha R}{\beta +\alpha R}}\\&={\frac {R}{{\tfrac {\beta }{\alpha }}+R}}\end{aligned}}$

Дифференциация относительно. R дает PDF-файл R

$f_{R}(R)={\frac {d}{dR}}\left({\frac {R}{{\tfrac {\beta }{\alpha }}+R}}\right)={\frac {\tfrac {\beta }{\alpha }}{\left({\tfrac {\beta }{\alpha }}+R\right)^{2}}}$

Моменты случайных отношений

Из теории преобразования Меллина для распределений, существующих только на положительной полупрямой. $x\geq 0$, у нас есть идентичность продукта $\operatorname {E} [(UV)^{p}]=\operatorname {E} [U^{p}]\;\;\operatorname {E} [V^{p}]$ предоставил $U,\;V$ независимы. Для случая соотношения выборок типа $\operatorname {E} [(X/Y)^{p}]$, чтобы воспользоваться этим тождеством, необходимо использовать моменты обратного распределения. Набор $1/Y=Z$ такой, что $\operatorname {E} [(XZ)^{p}]=\operatorname {E} [X^{p}]\;\operatorname {E} [Y^{-p}]$.Таким образом, если моменты $X^{p}$ и $Y^{-p}$ можно определить отдельно, то моменты $X/Y$ можно найти. Моменты $Y^{-p}$ определяются из обратного PDF-файла $Y$ , часто легкое упражнение. В самом простом случае, ${\textstyle \operatorname {E} [Y^{-p}]=\int _{0}^{\infty }y^{-p}f_{y}(y)\,dy}$.

Для иллюстрации позвольте $X$ быть выбран из стандартного гамма-распределения

$x^{\alpha -1}e^{-x}/\Gamma (\alpha )$ чей $p$-й момент $\Gamma (\alpha +p)/\Gamma (\alpha )$.

$Z=Y^{-1}$выбирается из обратного гамма-распределения с параметром $\beta$ и есть pdf $\;\Gamma ^{-1}(\beta )z^{1+\beta }e^{-1/z}$. Моменты этого PDF-файла

$\operatorname {E} [Z^{p}]=\operatorname {E} [Y^{-p}]={\frac {\Gamma (\beta -p)}{\Gamma (\beta )}},\;p<\beta .$

Умножение соответствующих моментов дает

$\operatorname {E} [(X/Y)^{p}]=\operatorname {E} [X^{p}]\;\operatorname {E} [Y^{-p}]={\frac {\Gamma (\alpha +p)}{\Gamma (\alpha )}}{\frac {\Gamma (\beta -p)}{\Gamma (\beta )}},\;p<\beta .$

Независимо известно, что соотношение двух образцов Гаммы $R=X/Y$ соответствует дистрибутиву Beta Prime:

$f_{\beta '}(r,\alpha ,\beta )=B(\alpha ,\beta )^{-1}r^{\alpha -1}(1+r)^{-(\alpha +\beta )}$ чьи моменты $\operatorname {E} [R^{p}]={\frac {\mathrm {B} (\alpha +p,\beta -p)}{\mathrm {B} (\alpha ,\beta )}}$

Замена $\mathrm {B} (\alpha ,\beta )={\frac {\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}}$ у нас есть $\operatorname {E} [R^{p}]={\frac {\Gamma (\alpha +p)\Gamma (\beta -p)}{\Gamma (\alpha +\beta )}}{\Bigg /}{\frac {\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}}={\frac {\Gamma (\alpha +p)\Gamma (\beta -p)}{\Gamma (\alpha )\Gamma (\beta )}}$что согласуется с произведением моментов выше.

Средние и дисперсии случайных отношений

В разделе «Распределение продуктов» , полученном на основе теории преобразования Меллина (см. раздел выше), обнаружено, что среднее значение произведения независимых переменных равно произведению их средних значений. В случае отношений имеем

$\operatorname {E} (X/Y)=\operatorname {E} (X)\operatorname {E} (1/Y)$

что с точки зрения распределения вероятностей эквивалентно

$\operatorname {E} (X/Y)=\int _{-\infty }^{\infty }xf_{x}(x)\,dx\times \int _{-\infty }^{\infty }y^{-1}f_{y}(y)\,dy$

Обратите внимание, что $\operatorname {E} (1/Y)\neq {\frac {1}{\operatorname {E} (Y)}}$ то есть, $\int _{-\infty }^{\infty }y^{-1}f_{y}(y)\,dy\neq {\frac {1}{\int _{-\infty }^{\infty }yf_{y}(y)\,dy}}$

Дисперсия отношения независимых переменных равна

${\begin{aligned}\operatorname {Var} (X/Y)&=\operatorname {E} ([X/Y]^{2})-\operatorname {E^{2}} (X/Y)\\&=\operatorname {E} (X^{2})\operatorname {E} (1/Y^{2})-\operatorname {E} ^{2}(X)\operatorname {E} ^{2}(1/Y)\end{aligned}}$

Нормальные распределения отношений

Некоррелированное центральное нормальное соотношение

Когда X и Y независимы и имеют распределение Гаусса с нулевым средним значением, формой распределения их отношений является распределение Коши .Это можно получить, установив $Z=X/Y=\tan \theta$ потом покажу это $\theta$ имеет круговую симметрию. Для двумерного некоррелированного распределения Гаусса мы имеем

${\begin{aligned}p(x,y)&={\tfrac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}}\times {\tfrac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}y^{2}}\\&={\tfrac {1}{2\pi }}e^{-{\frac {1}{2}}(x^{2}+y^{2})}\\&={\tfrac {1}{2\pi }}e^{-{\frac {1}{2}}r^{2}}{\text{ with }}r^{2}=x^{2}+y^{2}\end{aligned}}$

Если $p(x,y)$ является функцией только r, тогда $\theta$ равномерно распределен по $[0,2\pi ]$ с плотностью $1/2\pi$ поэтому задача сводится к нахождению распределения вероятностей Z при отображении

$Z=X/Y=\tan \theta$

Имеем по сохранению вероятности

$p_{z}(z)|dz|=p_{\theta }(\theta )|d\theta |$

и поскольку $dz/d\theta =1/\cos ^{2}\theta$

$p_{z}(z)={\frac {p_{\theta }(\theta )}{|dz/d\theta |}}={\tfrac {1}{2\pi }}{\cos ^{2}\theta }$

и настройка ${\textstyle \cos ^{2}\theta ={\frac {1}{1+(\tan \theta )^{2}}}={\frac {1}{1+z^{2}}}}$ мы получаем

$p_{z}(z)={\frac {1/2\pi }{1+z^{2}}}$

Здесь присутствует ложный коэффициент 2. Фактически, два значения $\theta$ расстояние между $\pi$ отображается на то же значение z , плотность удваивается, и окончательный результат

$p_{z}(z)={\frac {1/\pi }{1+z^{2}}},\;\;-\infty <z<\infty$

Когда любое из двух нормальных распределений нецентрально, результат распределения отношения намного сложнее и приводится ниже в краткой форме, представленной Дэвидом Хинкли . Однако тригонометрический метод определения отношения распространяется на радиальные распределения, такие как двумерные нормали или двумерное уравнение Стьюдента , в которых плотность зависит только от радиуса. ${\textstyle r={\sqrt {x^{2}+y^{2}}}}$. Это не распространяется на отношение двух независимых t- распределений Стьюдента, которые дают соотношение Коши, показанное в разделе ниже для одной степени свободы.

Некоррелированное нецентральное нормальное соотношение

При отсутствии корреляции $(\operatorname {cor} (X,Y)=0)$, функция плотности вероятности двух нормальных переменных X = N ( µ _X , σ _X ² ) и Y знак равно N ( µ _Y , σ _Y ² ) соотношение Z = X / Y задается именно следующим выражением, полученным в нескольких источниках:

$p_{Z}(z)={\frac {b(z)\cdot d(z)}{a^{3}(z)}}{\frac {1}{{\sqrt {2\pi }}\sigma _{x}\sigma _{y}}}\left[\Phi \left({\frac {b(z)}{a(z)}}\right)-\Phi \left(-{\frac {b(z)}{a(z)}}\right)\right]+{\frac {1}{a^{2}(z)\cdot \pi \sigma _{x}\sigma _{y}}}e^{-{\frac {c}{2}}}$

где

$a(z)={\sqrt {{\frac {1}{\sigma _{x}^{2}}}z^{2}+{\frac {1}{\sigma _{y}^{2}}}}}$

$b(z)={\frac {\mu _{x}}{\sigma _{x}^{2}}}z+{\frac {\mu _{y}}{\sigma _{y}^{2}}}$

$c={\frac {\mu _{x}^{2}}{\sigma _{x}^{2}}}+{\frac {\mu _{y}^{2}}{\sigma _{y}^{2}}}$

$d(z)=e^{\frac {b^{2}(z)-ca^{2}(z)}{2a^{2}(z)}}$

и $\Phi$ — нормальная кумулятивная функция распределения :

$\Phi (t)=\int _{-\infty }^{t}\,{\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}u^{2}}\ du\,.$

• При нескольких предположениях (обычно реализуемых в практических приложениях) можно получить очень точную твердую аппроксимацию PDF. Основными преимуществами являются снижение сложности формул, CDF в закрытой форме, простое определение медианы, четко определенное управление ошибками и т. д. Для простоты давайте введем параметры: $p={\frac {\mu _{x}}{{\sqrt {2}}\sigma _{x}}}$, $q={\frac {\mu _{y}}{{\sqrt {2}}\sigma _{y}}}$ и $r={\frac {\mu _{x}}{\mu _{y}}}$. Тогда так называемое твердотельное приближение $p_{Z}^{\dagger }(z)$ к некоррелированному нецентральному нормальному отношению PDF выражается уравнением

$p_{Z}^{\dagger }(z)={\frac {1}{\sqrt {\pi }}}{\frac {p}{\mathrm {erf} [q]}}{\frac {1}{r}}{\frac {1+{\frac {p^{2}}{q^{2}}}{\frac {z}{r}}}{\left(1+{\frac {p^{2}}{q^{2}}}\left[{\frac {z}{r}}\right]^{2}\right)^{\frac {3}{2}}}}e^{-{\frac {p^{2}\left({\frac {z}{r}}-1\right)^{2}}{1+{\frac {p^{2}}{q^{2}}}\left[{\frac {z}{r}}\right]^{2}}}}$

• При определенных условиях возможна нормальная аппроксимация с дисперсией:

$\sigma _{z}^{2}={\frac {\mu _{x}^{2}}{\mu _{y}^{2}}}\left({\frac {\sigma _{x}^{2}}{\mu _{x}^{2}}}+{\frac {\sigma _{y}^{2}}{\mu _{y}^{2}}}\right)$

Коррелированное центральное нормальное соотношение

Приведенное выше выражение становится более сложным, когда переменные X и Y коррелируют. Если $\mu _{x}=\mu _{y}=0$ но $\sigma _{X}\neq \sigma _{Y}$ и $\rho \neq 0$ получается более общее распределение Коши

$p_{Z}(z)={\frac {1}{\pi }}{\frac {\beta }{(z-\alpha )^{2}+\beta ^{2}}},$

где ρ — коэффициент корреляции между X и Y и

$\alpha =\rho {\frac {\sigma _{x}}{\sigma _{y}}},$

$\beta ={\frac {\sigma _{x}}{\sigma _{y}}}{\sqrt {1-\rho ^{2}}}.$

Сложное распределение также было выражено с помощью вырожденной гипергеометрической функции Куммера или функции Эрмита .

Коррелированное нецентральное нормальное соотношение

Это было показано в задаче 4.28 Springer 1979 года.

Преобразование в логарифмическую область было предложено Кацем (1978) (см. биномиальный раздел ниже). Пусть соотношение будет

$T\sim {\frac {\mu _{x}+\mathbb {N} (0,\sigma _{x}^{2})}{\mu _{y}+\mathbb {N} (0,\sigma _{y}^{2})}}={\frac {\mu _{x}+X}{\mu _{y}+Y}}={\frac {\mu _{x}}{\mu _{y}}}{\frac {1+{\frac {X}{\mu _{x}}}}{1+{\frac {Y}{\mu _{y}}}}}$.

Возьмите журналы, чтобы получить

$\log _{e}(T)=\log _{e}\left({\frac {\mu _{x}}{\mu _{y}}}\right)+\log _{e}\left(1+{\frac {X}{\mu _{x}}}\right)-\log _{e}\left(1+{\frac {Y}{\mu _{y}}}\right).$

С $\log _{e}(1+\delta )=\delta -{\frac {\delta ^{2}}{2}}+{\frac {\delta ^{3}}{3}}+\cdots$ тогда асимптотически

$\log _{e}(T)\approx \log _{e}\left({\frac {\mu _{x}}{\mu _{y}}}\right)+{\frac {X}{\mu _{x}}}-{\frac {Y}{\mu _{y}}}\sim \log _{e}\left({\frac {\mu _{x}}{\mu _{y}}}\right)+\mathbb {N} \left(0,{\frac {\sigma _{x}^{2}}{\mu _{x}^{2}}}+{\frac {\sigma _{y}^{2}}{\mu _{y}^{2}}}\right).$

Альтернативно, Гири (1930) предположил, что

$t\approx {\frac {\mu _{y}T-\mu _{x}}{\sqrt {\sigma _{y}^{2}T^{2}-2\rho \sigma _{x}\sigma _{y}T+\sigma _{x}^{2}}}}$

имеет примерно стандартное распределение Гаусса : Это преобразование получило название преобразования Гири – Хинкли ; аппроксимация хороша, если Y вряд ли примет отрицательные значения, в основном $\mu _{y}>3\sigma _{y}$.

Точное коррелированное нецентральное нормальное соотношение

Это развито Дейлом (Спрингер, 1979, проблема 4.28) и Хинкли, 1969. Гири показал, как коррелированное отношение $z$ можно было преобразовать в форму, близкую к гауссовой, и разработать приближение для $t$ зависит от вероятности отрицательных значений знаменателя $x+\mu _{x}<0$ быть исчезающе малым. Более поздний анализ корреляционных отношений, проведенный Филлером, точен, но необходима осторожность при сочетании современных математических пакетов с вербальными условиями из старой литературы. Фам-Гиа подробно обсудил эти методы. Коррелированные результаты Хинкли точны, но ниже показано, что условие коррелированного отношения также может быть преобразовано в некоррелированное, поэтому требуются только приведенные выше упрощенные уравнения Хинкли, а не полная версия коррелированного отношения.

Пусть соотношение будет:

$z={\frac {x+\mu _{x}}{y+\mu _{y}}}$

в котором $x,y$ являются коррелированными нормальными переменными с нулевым средним с дисперсиями $\sigma _{x}^{2},\sigma _{y}^{2}$ и $X,Y$ иметь средства $\mu _{x},\mu _{y}.$Писать $x'=x-\rho y\sigma _{x}/\sigma _{y}$ такой, что $x',y$ становятся некоррелированными и $x'$ имеет стандартное отклонение

$\sigma _{x}'=\sigma _{x}{\sqrt {1-\rho ^{2}}}.$

Соотношение:

$z={\frac {x'+\rho y\sigma _{x}/\sigma _{y}+\mu _{x}}{y+\mu _{y}}}$

инвариантен относительно этого преобразования и сохраняет тот же PDF-файл. $y$ член в числителе, по-видимому, можно разделить путем расширения:

${x'+\rho y\sigma _{x}/\sigma _{y}+\mu _{x}}=x'+\mu _{x}-\rho \mu _{y}{\frac {\sigma _{x}}{\sigma _{y}}}+\rho (y+\mu _{y}){\frac {\sigma _{x}}{\sigma _{y}}}$

получить

$z={\frac {x'+\mu _{x}'}{y+\mu _{y}}}+\rho {\frac {\sigma _{x}}{\sigma _{y}}}$

в котором ${\textstyle \mu '_{x}=\mu _{x}-\rho \mu _{y}{\frac {\sigma _{x}}{\sigma _{y}}}}$ и z теперь стало отношением некоррелированных нецентральных нормальных выборок с инвариантным z -смещением (это формально не доказано, хотя, похоже, использовалось Гири),

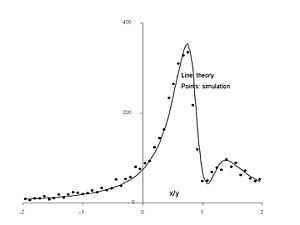
Наконец, чтобы быть ясным, PDF отношения $z$ для коррелированных переменных находится путем ввода измененных параметров $\sigma _{x}',\mu _{x}',\sigma _{y},\mu _{y}$ и $\rho '=0$ в уравнение Хинкли, приведенное выше, которое возвращает PDF-файл для коррелированного отношения с постоянным смещением $-\rho {\frac {\sigma _{x}}{\sigma _{y}}}$ на $z$.

Контуры коррелированного двумерного распределения Гаусса (не в масштабе), дающие соотношение x/y

pdf коэффициента Гаусса z и моделирование (в баллах) для
$\sigma _{x}=\sigma _{y}=1,\mu _{x}=0,\mu _{y}=0.5,\rho =0.975$

На рисунках выше показан пример положительно коррелированного соотношения с $\sigma _{x}=\sigma _{y}=1,\mu _{x}=0,\mu _{y}=0.5,\rho =0.975$ в котором заштрихованные клинья представляют собой приращение площади, выбранной по заданному соотношению. $x/y\in [r,r+\delta ]$ который накапливает вероятность там, где они перекрывают распределение. Теоретическое распределение, полученное на основе обсуждаемых уравнений в сочетании с уравнениями Хинкли, хорошо согласуется с результатами моделирования с использованием 5000 образцов. Из верхнего рисунка видно, что для отношения $z=x/y\approx 1$ клин почти полностью обошел основную массу распределения, и это объясняет локальный минимум в теоретическом PDF-файле. $p_{Z}(x/y)$. И наоборот, как $x/y$ движется либо к одному, либо от него, клин охватывает большую часть центральной массы, накапливая более высокую вероятность.

Комплексное нормальное соотношение

Отношение коррелированных нулевых среднесимметричных комплексных переменных с нормальным распределением было определено Baxley et al. и с тех пор был расширен до ненулевого и несимметричного случая. В случае коррелированного нулевого среднего совместное распределение x , y равно

$f_{x,y}(x,y)={\frac {1}{\pi ^{2}|\Sigma |}}\exp \left(-{\begin{bmatrix}x\\y\end{bmatrix}}^{H}\Sigma ^{-1}{\begin{bmatrix}x\\y\end{bmatrix}}\right)$

где

$\Sigma ={\begin{bmatrix}\sigma _{x}^{2}&\rho \sigma _{x}\sigma _{y}\\\rho ^{*}\sigma _{x}\sigma _{y}&\sigma _{y}^{2}\end{bmatrix}},\;\;x=x_{r}+ix_{i},\;\;y=y_{r}+iy_{i}$

$(\cdot )^{H}$ является эрмитовым транспонированием и

$\rho =\rho _{r}+i\rho _{i}=\operatorname {E} {\bigg (}{\frac {xy^{*}}{\sigma _{x}\sigma _{y}}}{\bigg )}\;\;\in \;\left|\mathbb {C} \right|\leq 1$

PDF-файл $Z=X/Y$ оказывается

${\begin{aligned}f_{z}(z_{r},z_{i})&={\frac {1-|\rho |^{2}}{\pi \sigma _{x}^{2}\sigma _{y}^{2}}}{\Biggr (}{\frac {|z|^{2}}{\sigma _{x}^{2}}}+{\frac {1}{\sigma _{y}^{2}}}-2{\frac {\rho _{r}z_{r}-\rho _{i}z_{i}}{\sigma _{x}\sigma _{y}}}{\Biggr )}^{-2}\\&={\frac {1-|\rho |^{2}}{\pi \sigma _{x}^{2}\sigma _{y}^{2}}}{\Biggr (}\;\;{\Biggr |}{\frac {z}{\sigma _{x}}}-{\frac {\rho ^{*}}{\sigma _{y}}}{\Biggr |}^{2}+{\frac {1-|\rho |^{2}}{\sigma _{y}^{2}}}{\Biggr )}^{-2}\end{aligned}}$

В обычном случае, когда $\sigma _{x}=\sigma _{y}$ мы получаем

$f_{z}(z_{r},z_{i})={\frac {1-|\rho |^{2}}{\pi \left(\;\;|z-\rho ^{*}|^{2}+1-|\rho |^{2}\right)^{2}}}$

Также приведены дополнительные результаты в закрытой форме для CDF.

Отношение распределения коррелирующих комплексных переменных, rho = 0,7 exp(i pi/4).

На графике показана PDF отношения двух комплексных нормальных переменных с коэффициентом корреляции $\rho =0.7\exp(i\pi /4)$. Пик pdf происходит примерно на уровне комплексного сопряжения уменьшенного $\rho$.

Отношение логнормального

Отношение независимых или коррелированных логарифмически нормальных значений является логарифмически нормальным. Это следует из того, что если $X_{1}$ и $X_{2}$ распределены логнормально , то $\ln(X_{1})$ и $\ln(X_{2})$ нормально распределены. Если они независимы или их логарифмы подчиняются двумерному нормальному распределению , то логарифм их отношения представляет собой разность независимых или коррелирующих нормально распределенных случайных величин, которая имеет нормальное распределение.

Это важно для многих приложений, требующих, чтобы отношение случайных величин было положительным, где совместное распределение $X_{1}$ и $X_{2}$ адекватно аппроксимируется логнормальным. Это общий результат мультипликативной центральной предельной теоремы , также известной как закон Гибрата , когда $X_{i}$ является результатом накопления множества небольших процентных изменений и должен быть положительным и иметь приблизительно логарифмически нормальное распределение.

Равномерное распределение коэффициентов

С двумя независимыми случайными величинами, имеющими равномерное распределение , например,

$p_{X}(x)={\begin{cases}1&0<x<1\\0&{\text{otherwise}}\end{cases}}$

соотношение распределения становится

$p_{Z}(z)={\begin{cases}1/2\qquad &0<z<1\\{\frac {1}{2z^{2}}}\qquad &z\geq 1\\0\qquad &{\text{otherwise}}\end{cases}}$

Распределение коэффициента Коши

Если две независимые случайные величины, каждая X и Y подчиняются распределению Коши с медианой, равной нулю, и коэффициентом формы $a$

$p_{X}(x|a)={\frac {a}{\pi (a^{2}+x^{2})}}$

тогда распределение отношения для случайной величины $Z=X/Y$ является

$p_{Z}(z|a)={\frac {1}{\pi ^{2}(z^{2}-1)}}\ln(z^{2}).$

Это распределение не зависит от $a$ и результат, заявленный Спрингером (стр. 158, вопрос 4.6) неверно.Распределение отношения похоже на распределение произведения случайной величины, но не совпадает с ним. $W=XY$:

$p_{W}(w|a)={\frac {a^{2}}{\pi ^{2}(w^{2}-a^{4})}}\ln \left({\frac {w^{2}}{a^{4}}}\right).$

В более общем смысле, если каждая из двух независимых случайных величин X и Y подчиняется распределению Коши с медианой, равной нулю, и коэффициентом формы $a$ и $b$ соответственно, тогда:

1. Распределение отношения для случайной величины $Z=X/Y$ является $$p_{Z}(z|a,b)={\frac {ab}{\pi ^{2}(b^{2}z^{2}-a^{2})}}\ln \left({\frac {b^{2}z^{2}}{a^{2}}}\right).$$
2. Распределение продукта для случайной величины $W=XY$ является $$p_{W}(w|a,b)={\frac {ab}{\pi ^{2}(w^{2}-a^{2}b^{2})}}\ln \left({\frac {w^{2}}{a^{2}b^{2}}}\right).$$

Результат распределения отношения можно получить из распределения продукта, заменив $b$ с ${\frac {1}{b}}.$

Соотношение стандартной обычной и стандартной униформы

Основная статья: Распространение Слэша

Если X имеет стандартное нормальное распределение, а Y имеет стандартное равномерное распределение, то Z = X / Y имеет распределение, известное как распределение косой черты , с функцией плотности вероятности.

$p_{Z}(z)={\begin{cases}\left[\varphi (0)-\varphi (z)\right]/z^{2}\quad &z\neq 0\\\varphi (0)/2\quad &z=0,\\\end{cases}}$

где φ( z ) — функция плотности вероятности стандартного нормального распределения.

Распределения Хи-квадрат, Гамма, Бета

Пусть G — нормальное (0,1) распределение, Y и Z — распределения хи-квадрат с m и n степенями свободы соответственно, все независимы, с $f_{\chi }(x,k)={\frac {x^{{\frac {k}{2}}-1}e^{-x/2}}{2^{k/2}\Gamma (k/2)}}$. Затем

${\frac {G}{\sqrt {Y/m}}}\sim t_{m}$ Стьюдента ​ ​ распределение

${\frac {Y/m}{Z/n}}=F_{m,n}$ Фишера F-критерия т.е. распределение

${\frac {Y}{Y+Z}}\sim \beta ({\tfrac {m}{2}},{\tfrac {n}{2}})$ бета -распределение

$\;\;{\frac {Y}{Z}}\sim \beta '({\tfrac {m}{2}},{\tfrac {n}{2}})$ стандартное распределение бета-простое

Если $V_{1}\sim {\chi '}_{k_{1}}^{2}(\lambda )$, нецентральное распределение хи-квадрат , и $V_{2}\sim {\chi '}_{k_{2}}^{2}(0)$ и $V_{1}$ не зависит от $V_{2}$ затем

${\frac {V_{1}/k_{1}}{V_{2}/k_{2}}}\sim F'_{k_{1},k_{2}}(\lambda )$, нецентральное F-распределение .

${\frac {m}{n}}F'_{m,n}=\beta '({\tfrac {m}{2}},{\tfrac {n}{2}}){\text{ or }}F'_{m,n}=\beta '({\tfrac {m}{2}},{\tfrac {n}{2}},1,{\tfrac {n}{m}})$ определяет $F'_{m,n}$, распределение плотности Фишера F, PDF отношения двух хи-квадратов с m, n степенями свободы.

CDF плотности Фишера, найденный в F -таблицах, определен в статье о бета-простом распределении . Если мы введем таблицу F -теста с m = 3, n = 4 и вероятностью 5% в правом хвосте, критическое значение окажется равным 6,59. Это совпадает с интегралом

$F_{3,4}(6.59)=\int _{6.59}^{\infty }\beta '(x;{\tfrac {m}{2}},{\tfrac {n}{2}},1,{\tfrac {n}{m}})dx=0.05$

Для гамма-распределений U и V с произвольными параметрами формы α ₁ и α ₂ и их масштабными параметрами оба равны единице, т.е. $U\sim \Gamma (\alpha _{1},1),V\sim \Gamma (\alpha _{2},1)$, где $\Gamma (x;\alpha ,1)={\frac {x^{\alpha -1}e^{-x}}{\Gamma (\alpha )}}$, затем

${\frac {U}{U+V}}\sim \beta (\alpha _{1},\alpha _{2}),\qquad {\text{ expectation }}={\frac {\alpha _{1}}{\alpha _{1}+\alpha _{2}}}$

${\frac {U}{V}}\sim \beta '(\alpha _{1},\alpha _{2}),\qquad \qquad {\text{ expectation }}={\frac {\alpha _{1}}{\alpha _{2}-1}},\;\alpha _{2}>1$

${\frac {V}{U}}\sim \beta '(\alpha _{2},\alpha _{1}),\qquad \qquad {\text{ expectation }}={\frac {\alpha _{2}}{\alpha _{1}-1}},\;\alpha _{1}>1$

Если $U\sim \Gamma (x;\alpha ,1)$, затем $\theta U\sim \Gamma (x;\alpha ,\theta )={\frac {x^{\alpha -1}e^{-{\frac {x}{\theta }}}}{\theta ^{k}\Gamma (\alpha )}}$. Обратите внимание, что здесь θ — это параметр масштаба , а не параметр скорости.

Если $U\sim \Gamma (\alpha _{1},\theta _{1}),\;V\sim \Gamma (\alpha _{2},\theta _{2})$, затем изменив масштаб $\theta$ параметр единицы у нас есть

${\frac {\frac {U}{\theta _{1}}}{{\frac {U}{\theta _{1}}}+{\frac {V}{\theta _{2}}}}}={\frac {\theta _{2}U}{\theta _{2}U+\theta _{1}V}}\sim \beta (\alpha _{1},\alpha _{2})$

${\frac {\frac {U}{\theta _{1}}}{\frac {V}{\theta _{2}}}}={\frac {\theta _{2}}{\theta _{1}}}{\frac {U}{V}}\sim \beta '(\alpha _{1},\alpha _{2})$

Таким образом

${\frac {U}{V}}\sim \beta '(\alpha _{1},\alpha _{2},1,{\frac {\theta _{1}}{\theta _{2}}})\quad {\text{ and }}\operatorname {E} \left[{\frac {U}{V}}\right]={\frac {\theta _{1}}{\theta _{2}}}{\frac {\alpha _{1}}{\alpha _{2}-1}}$

в котором $\beta '(\alpha ,\beta ,p,q)$ представляет собой обобщенное бета-распределение простых чисел .

Из вышесказанного очевидно, что если $X\sim \beta '(\alpha _{1},\alpha _{2},1,1)\equiv \beta '(\alpha _{1},\alpha _{2})$ затем $\theta X\sim \beta '(\alpha _{1},\alpha _{2},1,\theta )$. Более явно, поскольку

$\beta '(x;\alpha _{1},\alpha _{2},1,R)={\frac {1}{R}}\beta '({\frac {x}{R}};\alpha _{1},\alpha _{2})$

если $U\sim \Gamma (\alpha _{1},\theta _{1}),V\sim \Gamma (\alpha _{2},\theta _{2})$ затем

${\frac {U}{V}}\sim {\frac {1}{R}}\beta '({\frac {x}{R}};\alpha _{1},\alpha _{2})={\frac {\left({\frac {x}{R}}\right)^{\alpha _{1}-1}}{\left(1+{\frac {x}{R}}\right)^{\alpha _{1}+\alpha _{2}}}}\cdot {\frac {1}{\;R\;B(\alpha _{1},\alpha _{2})}},\;\;x\geq 0$

где

$R={\frac {\theta _{1}}{\theta _{2}}},\;\;\;B(\alpha _{1},\alpha _{2})={\frac {\Gamma (\alpha _{1})\Gamma (\alpha _{2})}{\Gamma (\alpha _{1}+\alpha _{2})}}$

Рэлеевские распределения

Если X , Y являются независимыми выборками из распределения Рэлея $f_{r}(r)=(r/\sigma ^{2})e^{-r^{2}/2\sigma ^{2}},\;\;r\geq 0$, отношение Z = X / Y подчиняется распределению

$f_{z}(z)={\frac {2z}{(1+z^{2})^{2}}},\;\;z\geq 0$

и имеет cdf

$F_{z}(z)=1-{\frac {1}{1+z^{2}}}={\frac {z^{2}}{1+z^{2}}},\;\;\;z\geq 0$

Распределение Рэлея имеет масштабирование в качестве единственного параметра. Распределение $Z=\alpha X/Y$ следует

$f_{z}(z,\alpha )={\frac {2\alpha z}{(\alpha +z^{2})^{2}}},\;\;z>0$

и имеет cdf

$F_{z}(z,\alpha )={\frac {z^{2}}{\alpha +z^{2}}},\;\;\;z\geq 0$

Дробные гамма-распределения (включая хи, хи-квадрат, экспоненциальное, Рэлея и Вейбулла)

Обобщенное гамма- распределение

$f(x;a,d,r)={\frac {r}{\Gamma (d/r)a^{d}}}x^{d-1}e^{-(x/a)^{r}}\;x\geq 0;\;\;a,\;d,\;r>0$

который включает в себя регулярные распределения гаммы, хи, хи-квадрат, экспоненциальное, Рэлея, Накагами и Вейбулла, включающие дробные степени. Обратите внимание, что здесь a — параметр масштаба , а не параметр скорости; d — параметр формы.

Если $U\sim f(x;a_{1},d_{1},r),\;\;V\sim f(x;a_{2},d_{2},r){\text{ are independent, and }}W=U/V$

затем ${\textstyle g(w)={\frac {r\left({\frac {a_{1}}{a_{2}}}\right)^{d_{2}}}{B\left({\frac {d_{1}}{r}},{\frac {d_{2}}{r}}\right)}}{\frac {w^{-d_{2}-1}}{\left(1+\left({\frac {a_{2}}{a_{1}}}\right)^{-r}w^{-r}\right)^{\frac {d_{1}+d_{2}}{r}}}},\;\;w>0}$

где $B(u,v)={\frac {\Gamma (u)\Gamma (v)}{\Gamma (u+v)}}$

Моделирование комбинации различных коэффициентов масштабирования

В приведенных выше соотношениях образцы гаммы, U , V могут иметь разные размеры выборок. $\alpha _{1},\alpha _{2}$ но должны быть взяты из того же дистрибутива ${\frac {x^{\alpha -1}e^{-{\frac {x}{\theta }}}}{\theta ^{k}\Gamma (\alpha )}}$ с равным масштабированием $\theta$.

В ситуациях, когда U и V масштабируются по-разному, преобразование переменных позволяет определить модифицированное случайное соотношение pdf. Позволять $X={\frac {U}{U+V}}={\frac {1}{1+B}}$ где $U\sim \Gamma (\alpha _{1},\theta ),V\sim \Gamma (\alpha _{2},\theta ),\theta$ произвольно и сверху $X\sim Beta(\alpha _{1},\alpha _{2}),B=V/U\sim Beta'(\alpha _{2},\alpha _{1})$.

Измените масштаб V произвольно, определив $Y\sim {\frac {U}{U+\varphi V}}={\frac {1}{1+\varphi B}},\;\;0\leq \varphi \leq \infty$

У нас есть $B={\frac {1-X}{X}}$ и замена на Y дает $Y={\frac {X}{\varphi +(1-\varphi )X}},dY/dX={\frac {\varphi }{(\varphi +(1-\varphi )X)^{2}}}$

Преобразование X в Y дает $f_{Y}(Y)={\frac {f_{X}(X)}{|dY/dX|}}={\frac {\beta (X,\alpha _{1},\alpha _{2})}{\varphi /[\varphi +(1-\varphi )X]^{2}}}$

Отмечая $X={\frac {\varphi Y}{1-(1-\varphi )Y}}$ у нас наконец-то есть

$f_{Y}(Y,\varphi )={\frac {\varphi }{[1-(1-\varphi )Y]^{2}}}\beta \left({\frac {\varphi Y}{1-(1-\varphi )Y}},\alpha _{1},\alpha _{2}\right),\;\;\;0\leq Y\leq 1$

Таким образом, если $U\sim \Gamma (\alpha _{1},\theta _{1})$ и $V\sim \Gamma (\alpha _{2},\theta _{2})$
затем $Y={\frac {U}{U+V}}$ распространяется как $f_{Y}(Y,\varphi )$ с $\varphi ={\frac {\theta _{2}}{\theta _{1}}}$

Распределение Y здесь ограничено интервалом [0,1]. Его можно обобщить путем масштабирования так, что если $Y\sim f_{Y}(Y,\varphi )$ затем

$\Theta Y\sim f_{Y}(Y,\varphi ,\Theta )$

где $f_{Y}(Y,\varphi ,\Theta )={\frac {\varphi /\Theta }{[1-(1-\varphi )Y/\Theta ]^{2}}}\beta \left({\frac {\varphi Y/\Theta }{1-(1-\varphi )Y/\Theta }},\alpha _{1},\alpha _{2}\right),\;\;\;0\leq Y\leq \Theta$

$\Theta Y$ тогда это образец из ${\frac {\Theta U}{U+\varphi V}}$

Обратные выборки из бета-распределений

Следующие тождества для одной переменной полезны, хотя и не являются соотношениями распределений двух переменных:

Если $X\sim \beta (\alpha ,\beta )$ затем $\mathbf {x} ={\frac {X}{1-X}}\sim \beta '(\alpha ,\beta )$

Если $\mathbf {Y} \sim \beta '(\alpha ,\beta )$ затем $y={\frac {1}{\mathbf {Y} }}\sim \beta '(\beta ,\alpha )$

объединение последних двух уравнений дает

Если $X\sim \beta (\alpha ,\beta )$ затем $\mathbf {x} ={\frac {1}{X}}-1\sim \beta '(\beta ,\alpha )$.

Если $\mathbf {Y} \sim \beta '(\alpha ,\beta )$ затем $y={\frac {\mathbf {Y} }{1+\mathbf {Y} }}\sim \beta (\alpha ,\beta )$

Следствие

${\frac {1}{1+\mathbf {Y} }}={\frac {\mathbf {Y} ^{-1}}{\mathbf {Y} ^{-1}+1}}\sim \beta (\beta ,\alpha )$

$1+\mathbf {Y} \sim \{\;\beta (\beta ,\alpha )\;\}^{-1}$, распределение обратных величин $\beta (\beta ,\alpha )$ образцы.

Если $U\sim \Gamma (\alpha ,1),V\sim \Gamma (\beta ,1)$ затем ${\frac {U}{V}}\sim \beta '(\alpha ,\beta )$ и

${\frac {U/V}{1+U/V}}={\frac {U}{V+U}}\sim \beta (\alpha ,\beta )$

Дополнительные результаты можно найти в статье об обратном распределении .

• Если $X,\;Y$ являются независимыми экспоненциальными случайными величинами со средним значением µ , то X − Y является двойной экспоненциальной случайной величиной со средним значением 0 и масштабом µ .

Биномиальное распределение

Этот результат был получен Katz et al.

Предполагать $X\sim {\text{Binomial}}(n,p_{1})$ и $Y\sim {\text{Binomial}}(m,p_{2})$ и $X$, $Y$ независимы. Позволять $T={\frac {X/n}{Y/m}}$.

Затем $\log(T)$ примерно нормально распределяется со средним значением $\log(p_{1}/p_{2})$ и дисперсия ${\frac {(1/p_{1})-1}{n}}+{\frac {(1/p_{2})-1}{m}}$.

Распределение биномиального отношения имеет значение в клинических исследованиях: если распределение Т известно, как указано выше, можно оценить вероятность того, что данное соотношение возникнет чисто случайно, т.е. ложноположительное исследование. В ряде работ сравнивается устойчивость различных аппроксимаций биномиального отношения.

Распределения Пуассона и усеченные распределения Пуассона

В отношении переменных Пуассона R = X/Y возникает проблема: Y равно нулю с конечной вероятностью, поэтому R не определено. Чтобы противостоять этому, рассмотрим усеченное или цензурированное соотношение R' = X/Y', где нулевая выборка Y не учитывается. Более того, во многих исследованиях медицинского типа возникают систематические проблемы с надежностью нулевых выборок как X, так и Y, и в любом случае хорошей практикой может быть игнорирование нулевых выборок.

Вероятность того, что нулевая выборка Пуассона окажется $e^{-\lambda }$, общий PDF-файл усеченного слева распределения Пуассона имеет вид

${\tilde {p}}_{x}(x;\lambda )={\frac {1}{1-e^{-\lambda }}}{\frac {e^{-\lambda }\lambda ^{x}}{x!}},\;\;\;x\in 1,2,3,\cdots$

что в сумме равно единице. Следуя за Коэном, для n независимых испытаний многомерный усеченный PDF-файл имеет вид

${\tilde {p}}(x_{1},x_{2},\dots ,x_{n};\lambda )={\frac {1}{(1-e^{-\lambda })^{n}}}\prod _{i=1}^{n}{\frac {e^{-\lambda }\lambda ^{x_{i}}}{x_{i}!}},\;\;\;x_{i}\in 1,2,3,\cdots$

и вероятность журнала становится

$L=\ln({\tilde {p}})=-n\ln(1-e^{-\lambda })-n\lambda +\ln(\lambda )\sum _{1}^{n}x_{i}-\ln \prod _{1}^{n}(x_{i}!),\;\;\;x_{i}\in 1,2,3,\cdots$

При дифференцировании получаем

$dL/d\lambda ={\frac {-n}{1-e^{-\lambda }}}+{\frac {1}{\lambda }}\sum _{i=1}^{n}x_{i}$

и установка нуля дает оценку максимального правдоподобия ${\hat {\lambda }}_{ML}$

${\frac {{\hat {\lambda }}_{ML}}{1-e^{-{\hat {\lambda }}_{ML}}}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\bar {x}}$

Обратите внимание, что как ${\hat {\lambda }}\to 0$ затем ${\bar {x}}\to 1$ поэтому усеченная максимальная вероятность $\lambda$ оценка, хотя и правильная как для усеченного, так и для неусеченного распределения, дает усеченное среднее значение ${\bar {x}}$ значение, которое сильно смещено относительно неусеченного значения. Тем не менее оказывается, что ${\bar {x}}$ является достаточной статистикой для $\lambda$ с ${\hat {\lambda }}_{ML}$ зависит от данных только через выборочное среднее ${\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}$ в предыдущем уравнении, которое соответствует методологии обычного распределения Пуассона .

При отсутствии каких-либо решений в замкнутой форме, следующее приближенное обращение для усеченных $\lambda$ действует во всем диапазоне $0\leq \lambda \leq \infty ;\;1\leq {\bar {x}}\leq \infty$.

${\hat {\lambda }}={\bar {x}}-e^{-({\bar {x}}-1)}-0.07({\bar {x}}-1)e^{-0.666({\bar {x}}-1)}+\epsilon ,\;\;\;|\epsilon |<0.006$

который сравнивается с необрезанной версией, которая просто ${\hat {\lambda }}={\bar {x}}$. Принимая соотношение $R={\hat {\lambda }}_{X}/{\hat {\lambda }}_{Y}$ это допустимая операция, хотя ${\hat {\lambda }}_{X}$ может использовать неусеченную модель, в то время как ${\hat {\lambda }}_{Y}$ имеет усеченный слева.

Асимптотическая большая $n\lambda {\text{ variance of }}{\hat {\lambda }}$ (и граница Крамера–Рао ) равна

$\mathbb {Var} ({\hat {\lambda }})\geq -\left(\mathbb {E} \left[{\frac {\delta ^{2}L}{\delta \lambda ^{2}}}\right]_{\lambda ={\hat {\lambda }}}\right)^{-1}$

в котором замена L дает

${\frac {\delta ^{2}L}{\delta \lambda ^{2}}}=-n\left[{\frac {\bar {x}}{\lambda ^{2}}}-{\frac {e^{-\lambda }}{(1-e^{-\lambda })^{2}}}\right]$

Затем подставив ${\bar {x}}$ из приведенного выше уравнения мы получаем оценку дисперсии Коэна

$\mathbb {Var} ({\hat {\lambda }})\geq {\frac {\hat {\lambda }}{n}}{\frac {(1-e^{-{\hat {\lambda }}})^{2}}{1-({\hat {\lambda }}+1)e^{-{\hat {\lambda }}}}}$

Дисперсия точечной оценки среднего $\lambda$, на основе n испытаний, асимптотически уменьшается до нуля при увеличении n до бесконечности. Для маленьких $\lambda$ он отличается от усеченной дисперсии PDF в Springael например, кто цитирует отклонение

$\mathbb {Var} (\lambda )={\frac {\lambda /n}{1-e^{-\lambda }}}\left[1-{\frac {\lambda e^{-\lambda }}{1-e^{-\lambda }}}\right]$

для n образцов в усеченном слева PDF-файле, показанном в верхней части этого раздела. Коэн показал, что дисперсия оценки относительно дисперсии PDF, $\mathbb {Var} ({\hat {\lambda }})/\mathbb {Var} (\lambda )$, варьируется от 1 для больших $\lambda$ (100% эффективность) до 2 как $\lambda$ приближается к нулю (эффективность 50%).

Эти оценки параметров среднего и дисперсии вместе с параллельными оценками X могут применяться к нормальным или биномиальным аппроксимациям коэффициента Пуассона. Образцы из испытаний могут не подходить для процесса Пуассона; дальнейшее обсуждение усечения по Пуассону проведено Дитцем и Бонингом. и есть запись в Википедии о распределении Пуассона с нулевым усечением .

Двойное распределение Ломакса

Это распределение представляет собой соотношение двух распределений Лапласа . Пусть X и Y — стандартные одинаково распределенные по Лапласу случайные величины, и пусть z = X / Y . Тогда распределение вероятностей z будет

$f(x)={\frac {1}{2(1+|z|)^{2}}}$

Пусть среднее значение X и Y будет a . Тогда стандартное двойное распределение Ломакса симметрично относительно a .

Это распределение имеет бесконечное среднее значение и дисперсию.

Если Z имеет стандартное двойное распределение Ломакса, то 1/ Z также имеет стандартное двойное распределение Ломакса.

Стандартное распределение Ломакса является унимодальным и имеет более тяжелые хвосты, чем распределение Лапласа.

При 0 < a < 1 существует a -й момент.

$E(Z^{a})={\frac {\Gamma (1+a)}{\Gamma (1-a)}}$

где Γ – гамма-функция .

Распределения отношений в многомерном анализе

Распределения отношений также появляются в многомерном анализе . Если случайные матрицы X и Y подчиняются распределению Уишарта , то отношение определителей

$\varphi =|\mathbf {X} |/|\mathbf {Y} |$

пропорциональна произведению независимых F случайных величин. В случае, когда X и Y взяты из независимых стандартизированных распределений Уишарта , соотношение

$\Lambda ={|\mathbf {X} |/|\mathbf {X} +\mathbf {Y} |}$

имеет лямбда-распределение Уилкса .

Отношения квадратичных форм с участием матриц Уишарта

По отношению к матричным распределениям Уишарта, если $S\sim W_{p}(\Sigma ,\nu +1)$ представляет собой образец матрицы и вектора Уишарта $V$ произвольно, но статистически независимо, следствие 3.2.9 Мюрхеда государства

${\frac {V^{T}SV}{V^{T}\Sigma V}}\sim \chi _{\nu }^{2}$

Расхождение на единицу в числах выборок возникает из-за оценки выборочного среднего при формировании выборочной ковариации, что является следствием теоремы Кокрана . Сходным образом

${\frac {V^{T}\Sigma ^{-1}V}{V^{T}S^{-1}V}}\sim \chi _{\nu -p+1}^{2}$

что является теоремой 3.2.12 Мюрхеда

См. также

• Отношения между распределениями вероятностей
• Обратное распределение (также известное как взаимное распределение)
• Распространение продукции
• Оценщик соотношения
• Слэш-распределение

Внешние ссылки

• Распределение отношений в MathWorld
• Распределение нормального отношения в MathWorld
• Распределения отношений на MathPages