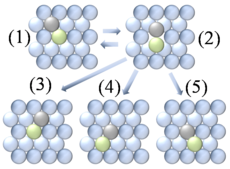
Поверхностная диффузия

Рисунок 1. Модель одиночного адатома , диффундирующего через квадратную поверхностную решетку. Обратите внимание, что частота вибрации адатома превышает скорость прыжка к близлежащим участкам. Кроме того, модель отображает примеры переходов как к ближайшему соседу (прямому), так и к следующему ближайшему соседу (по диагонали). Не масштабировать в пространстве или времени.

Поверхностная диффузия — общий процесс, включающий движение адатомов , молекул и кластеров атомов ( адчастиц ) по поверхностям твердого материала . ^[1] В целом этот процесс можно представить как перепрыгивание частиц между соседними участками адсорбции на поверхности, как показано на рисунке 1. Как и при объемной диффузии , это движение обычно представляет собой термически стимулируемый процесс, скорость которого увеличивается с увеличением температуры. Многие системы демонстрируют диффузионное поведение, которое отличается от традиционной модели скачков ближайших соседей. ^[2] Туннельная диффузия является особенно интересным примером нетрадиционного механизма, при котором было показано, что водород диффундирует на чистые металлические поверхности посредством эффекта квантового туннелирования .

механизмов и скорости поверхностной диффузии можно использовать различные аналитические инструменты Для выяснения , наиболее важными из которых являются полевая ионная микроскопия и сканирующая туннельная микроскопия . ^[3] Хотя в принципе этот процесс может происходить с различными материалами, большинство экспериментов проводится на кристаллических металлических поверхностях. Из-за экспериментальных ограничений большинство исследований поверхностной диффузии ограничиваются пределами температуры плавления подложки , и еще многое предстоит выяснить относительно того, как эти процессы происходят при более высоких температурах. ^[4]

На скорость и механизмы поверхностной диффузии влияют различные факторы, включая прочность связи поверхность-адчастица , ориентацию поверхностной решетки, притяжение и отталкивание между поверхностными частицами и градиенты химического потенциала . Это важная концепция в формировании поверхностной фазы , эпитаксиальном росте , гетерогенном катализе и других областях науки о поверхности . ^[5] Таким образом, принципы поверхностной диффузии имеют решающее значение для химического производства и полупроводниковой промышленности. Реальные приложения, в значительной степени зависящие от этих явлений, включают каталитические преобразователи , интегральные схемы, используемые в электронных устройствах, и соли галогенидов серебра , используемые в фотопленке . ^[5]

Кинетика [ править ]

Кинетику поверхностной диффузии можно рассматривать как адатомы, находящиеся в центрах адсорбции на двумерной решетке , перемещающиеся между соседними (ближайшими соседними) сайтами адсорбции посредством прыжкового процесса. ^[1]^[6] Скорость прыжка характеризуется частотой попыток и термодинамическим фактором, который определяет вероятность того, что попытка приведет к успешному прыжку. Частота попытки ν обычно считается просто частотой колебаний адатома, тогда как термодинамический фактор представляет собой фактор Больцмана, зависящий от температуры и E _diff , потенциального энергетического барьера для диффузии. Уравнение 1 описывает взаимосвязь:

\Gamma =\nu e^{-E_{\mathrm {diff} }/k_{B}T}\qquad {\text{(eq. 1)}}

Где ν и E _diff такие, как описано выше, Γ — скорость скачка или скачка, T — температура, а k _B — постоянная Больцмана . Для того чтобы произошла диффузия, E _diff должна быть меньше энергии десорбции, иначе процессы десорбции будут доминировать. Важно отметить, что уравнение 1 говорит нам, насколько сильно скорость скачка зависит от температуры. Способ, которым происходит диффузия, зависит от соотношения между E _diff и k _B T, как это указано в термодинамическом коэффициенте: когда E _diff < k _B T, термодинамический фактор приближается к единице, и E _diff перестает быть значимым барьером для диффузии. . Этот случай, известный как мобильная диффузия , является относительно редким и наблюдался лишь в нескольких системах. ^[7] Для явлений, описанных в этой статье, предполагается, что E _diff >> k _B T и, следовательно, Γ << ν . В случае диффузии Фика можно извлечь как ν, так и E _diff из графика Аррениуса логарифма коэффициента диффузии D в зависимости от 1/ T . В случаях, когда присутствует более одного механизма диффузии (см. ниже), может быть более одного E _diff, так что относительное распределение между различными процессами будет меняться с температурой.

Статистика случайных блужданий описывает среднеквадратичное смещение диффундирующих видов в терминах количества прыжков N и расстояния на каждый прыжок a . Число успешных прыжков — это просто Γ , умноженное на время, отведенное на диффузию t . В самой базовой модели учитываются только скачки ближайших соседей, а a соответствует расстоянию между центрами адсорбции ближайших соседей. Среднеквадратичное смещение выглядит следующим образом:

{\sqrt {\langle \Delta r^{2}\rangle }}=a{\sqrt {\Gamma t}}\qquad {\text{(eq. 2)}}

Коэффициент диффузии определяется как:

D={\frac {\Gamma a^{2}}{z}}\qquad {\text{(eq. 3)}}

где $z=2$ для одномерной диффузии, как и в случае внутриканальной диффузии, $z=4$ для 2D-диффузии и $z=6$ for 3D diffusion. ^[8]

Режимы [ править ]

Рисунок 3. Модель шести адатомов, диффундирующих по квадратной поверхностной решетке. Адатомы блокируют перемещение друг друга в соседние места. Согласно закону Фика , поток направлен в направлении, противоположном градиенту концентрации, что является чисто статистическим эффектом. Модель не предназначена для демонстрации отталкивания или притяжения и не подлежит масштабированию в пространстве или времени.

Существует четыре различных общих схемы, в которых может иметь место диффузия. ^[9] Диффузия индикаторов и химическая диффузия различаются по уровню покрытия адсорбатом на поверхности, тогда как собственная диффузия и массообменная диффузия различаются по природе диффузионной среды. Диффузия индикаторов и внутренняя диффузия относятся к системам, в которых адчастицы находятся в относительно однородной среде, тогда как в химической и массообменной диффузии на адчастицы более сильно влияет их окружение.

Диффузия трассеров описывает движение отдельных адчастиц по поверхности при относительно низких уровнях покрытия. На этих низких уровнях (<0,01 монослоя ) взаимодействие частиц низкое, и можно считать, что каждая частица движется независимо от других. Одиночный атом, диффундирующий на рисунке 1, является хорошим примером диффузии индикатора.
Химическая диффузия описывает процесс на более высоком уровне покрытия, где эффекты притяжения или отталкивания между адатомами становятся важными. Эти взаимодействия служат для изменения подвижности адатомов. Грубо говоря, рисунок 3 показывает, как адатомы могут взаимодействовать на более высоких уровнях покрытия. У адатомов нет «выбора», кроме как сначала двигаться вправо, а соседние адатомы могут блокировать места адсорбции друг от друга.
Собственная диффузия происходит на однородной поверхности (например, без ступенек или вакансий ), такой как одна терраса, где нет ловушек или источников адатомов. Этот режим часто изучают с помощью полевой ионной микроскопии , где терраса представляет собой острый кончик образца, по которому диффундирует адчастица. Даже в случае чистой террасы на процесс может влиять неравномерность по краям террасы.
Массопереносная диффузия имеет место в том случае, если присутствуют источники и ловушки адчастиц, такие как изломы, ступеньки и вакансии. Вместо того чтобы зависеть только от потенциального барьера скачка E _diff , диффузия в этом режиме теперь зависит также от энергии образования мобильных адчастиц. Таким образом, точная природа диффузионной среды играет роль в определении скорости диффузии, поскольку энергия образования адчастицы различна для каждого типа поверхностных элементов, как описано в модели Terrace Ledge Kink .

Анизотропия [ править ]

Ориентационная анизотропия принимает форму различия как в скоростях, так и в механизмах диффузии при различных ориентациях поверхности данного материала. Для данного кристаллического материала каждая плоскость индекса Миллера может проявлять уникальные явления диффузии. Плотно упакованные поверхности, такие как ГЦК (111), имеют тенденцию иметь более высокие скорости диффузии, чем соответственно более «открытые» поверхности того же материала, такие как ГЦК (100). ^[10]^[11]

Направленная анизотропия относится к разнице в механизме или скорости диффузии в определенном направлении на данной кристаллографической плоскости. Эти различия могут быть результатом либо анизотропии поверхностной решетки (например, прямоугольной решетки ), либо наличия ступенек на поверхности. Одним из наиболее ярких примеров направленной анизотропии является диффузия адатомов на каналированных поверхностях, таких как ГЦК (110), где диффузия вдоль канала происходит намного быстрее, чем диффузия поперек канала.

Механизмы [ править ]

Диффузия адатомов [ править ]

Диффузия адатомов может происходить по разным механизмам. Способ их диффузии важен, поскольку он может определять, среди других параметров, кинетику движения, температурную зависимость и общую подвижность поверхностных частиц. Ниже приводится краткое изложение наиболее важных из этих процессов: ^[12]

Прыжок или скачок концептуально является самым основным механизмом диффузии адатомов. В этой модели адатомы располагаются в адсорбционных центрах поверхностной решетки. Движение происходит за счет последовательных прыжков на соседние узлы, число которых зависит от характера решетки поверхности. На рисунках 1 и 3 показаны адатомы, подвергающиеся диффузии в результате прыжкового процесса. Исследования показали наличие метастабильных переходных состояний между местами адсорбции, в которых адатомы могут временно находиться. ^[13]
Атомный обмен включает обмен между адатомом и соседним атомом внутри поверхностной решетки. Как показано на рисунке 4, после события атомного обмена адатом занял место поверхностного атома, а поверхностный атом сместился и теперь стал адатомом. Этот процесс может происходить как при гетеродиффузии (например, адатомы Pt на Ni ), так и при самодиффузии (например, адатомы Pt на Pt). С теоретической точки зрения до сих пор неясно, почему в одних системах механизм атомного обмена преобладает больше, чем в других. Современная теория указывает на множество возможностей, включая растягивающие поверхностные напряжения, поверхностную релаксацию адатома и повышенную стабильность промежуточного продукта из-за того, что оба участвующих атома поддерживают высокий уровень координации на протяжении всего процесса. ^[14]^[15]
Туннельная диффузия — это физическое проявление эффекта квантового туннелирования, включающего туннелирование частиц через диффузионные барьеры. Это может произойти в случае малой массы диффундирующих частиц и низкой E _diff и наблюдалось в случае диффузии водорода на поверхности вольфрама и меди . ^[16] Уникальность явления состоит в том, что в режиме доминирования туннельного механизма скорость диффузии практически не зависит от температуры. ^[17]
Диффузия вакансий может происходить как преобладающий метод поверхностной диффузии при высоких уровнях покрытия, приближающихся к полному покрытию. Этот процесс подобен тому, как кусочки скользят в « скользящей головоломке ». Очень трудно непосредственно наблюдать диффузию вакансий из-за обычно высоких скоростей диффузии и низкой концентрации вакансий . ^[18] На рисунке 5 показана основная тема этого механизма, хотя и в упрощенном виде.

Рис. 6. Механизмы поверхностного диффузионного скачка. Схема различных скачков, которые могут иметь место на квадратной решетке, такой как плоскость ГЦК (100). 1) Розовый атом совершает прыжки разной длины в позиции 2–5; 6) Зеленый атом совершает диагональный прыжок в позицию 7; 8) Серый атом совершает отскок (атом оказывается там же, где и стартовал). Скачки не через ближайших соседей обычно происходят с большей частотой при более высоких температурах. Не в масштабе.	Рисунок 7. График, показывающий распределение относительной вероятности смещения адатома Δx при диффузии в одном измерении. Синий: только одиночные прыжки; Розовый: происходят двойные скачки, соотношение одинарных:двойных скачков = 1. Статистический анализ данных может дать информацию о механизме диффузии.
Рисунок 8. Межканальная диффузия с участием адатома (серого цвета) на каналированной поверхности (например, ГЦК (110), синий плюс выделенный зеленым атом). 1) Первоначальная настройка; 2) Промежуточная конфигурация «Гантель». Окончательное перемещение может включать 3, 4, 5 или даже возврат к исходной конфигурации. Не в масштабе.	Рисунок 9. Механизм дальнего атомного обмена для поверхностной диффузии в квадратной решетке. Адатом (розовый), покоящийся на поверхности (1), внедряется в решетку, нарушая соседние атомы (2), в конечном итоге вызывая появление одного из исходных атомов подложки в виде адатома (зеленый) (3). Не в масштабе.

Недавние теоретические работы, а также экспериментальные работы, выполненные с конца 1970-х годов, выявили удивительное разнообразие явлений поверхностной диффузии как с точки зрения кинетики, так и механизмов. Ниже приводится краткое изложение некоторых наиболее примечательных явлений:

Длинные скачки состоят из смещения адатома к месту адсорбции, не являющемуся ближайшим соседом. предсказывает, Они могут включать в себя двойные, тройные и более длинные прыжки в том же направлении, в котором будет двигаться прыжок ближайшего соседа, или они могут совершаться в совершенно разных направлениях, как показано на рисунке 6. Теория что они существуют во многих различных системах. Экспериментально было показано, что это происходит при температурах всего 0,1 Т _м (температура плавления). В некоторых случаях данные указывают на то, что длинные скачки доминируют в процессе диффузии над одиночными скачками при повышенных температурах; Явление переменной длины прыжка выражается в различных характерных распределениях атомных смещений во времени (см. рисунок 7). ^[19]
скачки отскока Как эксперименты, так и моделирование показали, что в некоторых системах происходят . Поскольку движение не приводит к чистому смещению задействованного адатома, экспериментальные доказательства скачков отскока снова получены в результате статистической интерпретации распределения атомов. Скачок отскока показан на рисунке 6. Однако этот рисунок немного вводит в заблуждение, поскольку экспериментально было показано, что скачки отскока имеют место только в случае одномерной диффузии на каналированной поверхности (в частности, на ОЦК (211) грани вольфрама). ). ^[20]
Межканальная диффузия может происходить в случае канализированных поверхностей. Обычно внутриканальная диффузия доминирует из-за более низкого энергетического барьера для диффузии этого процесса. Было показано, что в некоторых случаях возникает перекрестный канал, происходящий аналогично тому, как показано на рисунке 8. Промежуточное положение «гантели» может привести к множеству конечных смещений адатомов и поверхностных атомов. ^[21]
Атомный обмен на большие расстояния - это процесс, включающий внедрение адатома в поверхность, как и в обычном механизме атомного обмена, но вместо атома ближайшего соседа появляется атом, находящийся на некотором расстоянии дальше от исходного адатома. Как показано на рисунке 9, этот процесс наблюдался только при моделировании молекулярной динамики и еще не подтвержден экспериментально. Несмотря на этот дальний атомный обмен, а также множество других экзотических механизмов диффузии, как ожидается, внесут существенный вклад при температурах, которые в настоящее время слишком высоки для прямого наблюдения. ^[22]

Кластерная диффузия [ править ]

Кластерная диффузия предполагает движение атомных кластеров размером от димеров до островков, содержащих сотни атомов. Движение кластера может происходить за счет смещения отдельных атомов, участков кластера или движения всего кластера одновременно. ^[23] скопления Все эти процессы связаны с изменением центра масс .

Индивидуальные механизмы — это те, которые включают движение одного атома за раз. ^[24]
- Краевая диффузия включает перемещение адатомов или вакансий по краям или в местах излома. Как показано на рисунке 10, мобильный атом сохраняет свою близость к кластеру на протяжении всего процесса.
- В процессе испарения-конденсации атомы « испаряются » из кластера на террасу, сопровождаясь « конденсацией » адатомов террасы на кластер, что приводит к изменению центра масс кластера. Хотя на рисунке 10 кажется, что один и тот же атом испаряется и конденсируется на кластере, на самом деле это может быть другой атом, конденсирующийся из двумерного газа.
- Диффузия «чехарда» аналогична краевой диффузии, но при этом диффундирующий атом фактически перемещается по вершине кластера, прежде чем оседать в другом месте по сравнению со своим исходным положением.
- Последовательное смещение относится к процессу, включающему движение одного атома за раз с перемещением к свободным местам ближайших соседей.


(а) Дислокация	(б) Скольжение

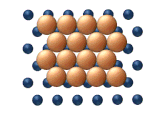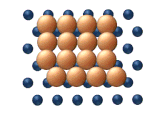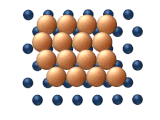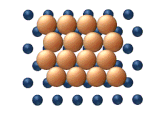(в) Рептация	(г) Сдвиг
Рисунок 11. Согласованные механизмы кластерной диффузии.

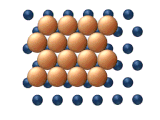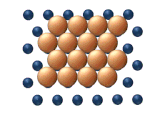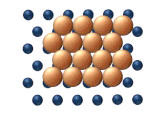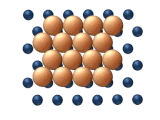
Согласованные механизмы — это те, которые предполагают движение либо частей кластера, либо всего кластера одновременно. ^[25]
- Диффузия дислокаций происходит, когда соседние субъединицы кластера движутся ряд за рядом посредством смещения дислокации . Как показано на рисунке 11(а), процесс начинается с зарождения дислокации, за которым следует, по сути, последовательное перемещение на согласованной основе.
- Скользящая диффузия относится к согласованному движению всего кластера одновременно (см. рисунок 11 (b)).
- Рептация — это змееподобное движение (отсюда и название), включающее последовательное движение субъединиц кластера (см. рисунок 11(c)).
- Сдвиг — это согласованное смещение части атомов внутри кластера (см. рисунок 11(d)).
Зависимость от размера : скорость диффузии кластера сильно зависит от размера кластера, причем больший размер кластера обычно соответствует более медленной диффузии. Однако это не универсальная тенденция, и в некоторых системах было показано, что скорость диффузии приобретает периодическую тенденцию, при которой некоторые более крупные кластеры диффундируют быстрее, чем меньшие по размеру. ^[26]

Поверхностная диффузия гетерогенный катализ и

Поверхностная диффузия является критически важной концепцией в гетерогенном катализе, поскольку скорость реакции часто определяется способностью реагентов «находить» друг друга на поверхности катализатора. При повышении температуры адсорбированные молекулы, молекулярные фрагменты, атомы и кластеры имеют тенденцию иметь гораздо большую подвижность (см. уравнение 1). Однако с повышением температуры время жизни адсорбции уменьшается, поскольку коэффициент k _B T становится достаточно большим, чтобы адсорбированные частицы могли преодолеть барьер десорбции Q (см. Рисунок 2). реакции Если оставить в стороне термодинамику , из-за взаимодействия между увеличением скорости диффузии и уменьшением времени жизни адсорбции повышение температуры может в некоторых случаях снизить общую скорость реакции.

Экспериментальный [ править ]

Поверхностную диффузию можно изучать различными методами, включая как прямые, так и косвенные наблюдения. Двумя экспериментальными методами, которые оказались очень полезными в этой области исследований, являются полевая ионная микроскопия и сканирующая туннельная микроскопия . ^[3] Визуализируя смещение атомов или кластеров с течением времени, можно получить полезную информацию о том, как распространяются соответствующие виды — как механистическую, так и информацию, связанную со скоростью. К сожалению, для изучения поверхностной диффузии в атомистическом масштабе необходимо проводить исследования на строго чистых поверхностях и в условиях сверхвысокого вакуума (СВВ) или в присутствии небольших количеств инертного газа, как в случае использования He или Ne. в качестве визуализирующего газа в экспериментах по полевой ионной микроскопии .

См. также [ править ]

Ссылки [ править ]

^ Jump up to: ^а ^б Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 325
^ Анчак, Эрлих 2007, стр.39
^ Jump up to: ^а ^б Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 349
^ Анчак, Эрлих 2007, стр. 50, 59.
^ Jump up to: ^а ^б Шусторович 1991, с. 109
^ Шусторович 1991, с. 109-111
^ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 327
^ Структура и динамика поверхностей II (темы современной физики), В. Шоммерс, П. Фон Бланкенхаген, ISBN 0387173382 . Глава 3.2, с. 75
^ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 330-333
^ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 333
^ Шусторович 1991, с. 114-115
^ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 336-340
^ Шусторович 1991, с. 111
^ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 338
^ Анчак, Эрлих 2007, стр. 48.
^ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 338-340
^ Шусторович 1991, с. 115
^ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 340-341
^ Анчак, Эрлих 2007, стр. 51.
^ Анчак, Эрлих 2007, стр. 58.
^ Анчак, Эрлих 2007, стр. 40-45.
^ Анчак, Эрлих 2007, стр. 48-50.
^ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 341
^ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 343-344
^ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 343-345
^ Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 341-343

Цитируемые работы [ править ]

Г. Анчак, Г. Эрлих. Отчеты о поверхностной науке 62 (2007), 39-61. (Обзор)
Оура, К.; В.Г. Лифшиц; А.А. Саранин; А.В. Зотов; М. Катаяма (2003). Наука о поверхности: Введение . Шпрингер-Верлаг Берлин Гейдельберг. ISBN 3-540-00545-5 .
Шусторович, Э. (1991). Энергетика реакций с металлической поверхностью: теория и приложения к гетерогенному катализу, хемосорбции и поверхностной диффузии . VCH Publishers, Inc. ISBN 3-527-27938-5 .

[Oura325-1] Jump up to: ^а ^б Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 325

[2] Анчак, Эрлих 2007, стр.39

[Oura,_Lifshits_2003,_p._349-3] Jump up to: ^а ^б Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 349

[4] Анчак, Эрлих 2007, стр. 50, 59.

[Shust109-5] Jump up to: ^а ^б Шусторович 1991, с. 109

[6] Шусторович 1991, с. 109-111

[7] Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 327

[8] Структура и динамика поверхностей II (темы современной физики), В. Шоммерс, П. Фон Бланкенхаген, ISBN 0387173382 . Глава 3.2, с. 75

[9] Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 330-333

[10] Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 333

[11] Шусторович 1991, с. 114-115

[12] Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 336-340

[13] Шусторович 1991, с. 111

[14] Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 338

[15] Анчак, Эрлих 2007, стр. 48.

[16] Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 338-340

[17] Шусторович 1991, с. 115

[18] Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 340-341

[19] Анчак, Эрлих 2007, стр. 51.

[20] Анчак, Эрлих 2007, стр. 58.

[21] Анчак, Эрлих 2007, стр. 40-45.

[22] Анчак, Эрлих 2007, стр. 48-50.

[23] Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 341

[24] Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 343-344

[25] Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 343-345

[26] Oura, Lifshits, Saranin, Zotov, and Katayama 2003, p. 341-343

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]