Длина волны

Чтобы узнать о других значениях, см. Длина волны (значения) .

Длину синусоидальной волны λ , например , можно измерить между любыми двумя точками с одинаковой фазой между гребнями (сверху), впадинами (внизу) или соответствующими пересечениями нуля , как показано.

В физике и математике — это расстояние , длина волны или пространственный период волны на котором повторяется или периодической функции форма волны. Другими словами, это расстояние между последовательными соответствующими точками одной и той же фазы на волне, например, двумя соседними гребнями, впадинами или пересечениями нуля . Длина волны является характеристикой как бегущих волн, так и стоячих волн , а также других пространственных волновых структур. Обратная длина волны называется пространственной частотой . Длина волны обычно обозначается греческой буквой лямбда ( λ ).Термин «длина волны» также иногда применяется к модулированным волнам, а также к синусоидальным огибающим модулированных волн или волн, образованных интерференцией нескольких синусоид.

Предполагая, что синусоидальная волна движется с фиксированной волновой скоростью, длина волны обратно пропорциональна частоте волны : волны с более высокими частотами имеют более короткие длины волн, а более низкие частоты имеют более длинные волны.

Длина волны зависит от среды (например, вакуума, воздуха или воды), через которую проходит волна. Примерами волн являются звуковые волны , свет , волны на воде и периодические электрические сигналы в проводнике . Звуковая электромагнитном волна — это изменение давления воздуха , тогда как в световом и другом излучении сила электрического и магнитного полей различается. Волны на воде – это изменения высоты водоема. При колебаниях кристаллической решетки положения атомов меняются.

Диапазон длин волн или частот волновых явлений называется спектром . Название произошло от спектра видимого света , но теперь может быть применено ко всему электромагнитному спектру , а также к звуковому спектру или спектру вибрации .

Синусоидальные волны

В линейных средах любую волновую картину можно описать с точки зрения независимого распространения синусоидальных составляющих. Длина волны λ синусоидального сигнала, движущегося с постоянной скоростью. $v$ дается

$\lambda ={\frac {v}{f}}\,\,,$

где $v$ называется фазовой скоростью (величиной фазовой скорости ) волны и $f$ волны это частота . В среде с дисперсией сама фазовая скорость зависит от частоты волны, что делает связь между длиной волны и частотой нелинейной.

В случае электромагнитного излучения , такого как свет, в свободном пространстве фазовая скорость равна скорости света , примерно 3 × 10. ⁸ РС . Таким образом, длина волны электромагнитной (радио) волны частотой 100 МГц составляет примерно: 3 × 10 ⁸ м/с разделить на 10 ⁸ Гц = 3 м. Длина волны видимого света колеблется от темно- красного , примерно 700 нм , до фиолетового , примерно 400 нм (другие примеры см. в разделе «Электромагнитный спектр »).

Для звуковых волн в воздухе скорость звука равна 343 м/с (при комнатной температуре и атмосферном давлении ). Таким образом, длины волн звуковых частот, слышимых человеческим ухом (20 Гц – 20 кГц), составляют примерно от 17 м до 17 мм соответственно. используют несколько более высокие частоты Летучие мыши , поэтому они могут различать цели размером менее 17 мм. Длины волн слышимого звука намного длиннее, чем волны видимого света.

Синусоидальные стоячие волны в рамке, которая ограничивает конечные точки узлами, будут иметь целое число половин длин волн, помещающихся в рамку.

Стоячая волна (черная), изображаемая как сумма двух распространяющихся волн, движущихся в противоположных направлениях (красная и синяя).

Стоячие волны

– Стоячая волна это волнообразное движение, которое остается на одном месте. Синусоидальная стоячая волна включает в себя стационарные точки неподвижности, называемые узлами , а длина волны в два раза превышает расстояние между узлами.

На верхнем рисунке показаны три стоячие волны в прямоугольнике. Считается, что стены ящика требуют, чтобы волна имела узлы на стенках ящика (пример граничных условий ), тем самым определяя разрешенные длины волн. Например, для электромагнитной волны, если ящик имеет идеальные проводящие стенки, условие для узлов на стенках возникает из-за того, что проводящие стенки не могут поддерживать тангенциальное электрическое поле, что приводит к тому, что волна имеет нулевую амплитуду у стены.

Стоячую волну можно рассматривать как сумму двух бегущих синусоидальных волн с противоположно направленными скоростями. Следовательно, длина волны, период и скорость волны связаны так же, как и для бегущей волны. Например, скорость света можно определить, наблюдая за стоячими волнами в металлическом ящике, содержащем идеальный вакуум.

Математическое представление

Бегущие синусоидальные волны часто представляются математически через их скорость v (в направлении x), частоту f и длину волны λ как:

$y(x,\ t)=A\cos \left(2\pi \left({\frac {x}{\lambda }}-ft\right)\right)=A\cos \left({\frac {2\pi }{\lambda }}(x-vt)\right)$

где y — значение волны в любой позиции x и времени t , а A — амплитуда волны. Их также обычно выражают через волновое число k (в 2π раз больше обратной длины волны) и угловую частоту ω (в 2π раза больше частоты) как:

$y(x,\ t)=A\cos \left(kx-\omega t\right)=A\cos \left(k(x-vt)\right)$

в котором длина волны и волновое число связаны со скоростью и частотой следующим образом:

$k={\frac {2\pi }{\lambda }}={\frac {2\pi f}{v}}={\frac {\omega }{v}},$

или

$\lambda ={\frac {2\pi }{k}}={\frac {2\pi v}{\omega }}={\frac {v}{f}}.$

Во второй форме, приведенной выше, фаза ( kx − ωt ) часто обобщается до ( k ⋅ r − ωt ) путем замены волнового числа k , волновым вектором который определяет направление и волновое число плоской волны в трехмерном пространстве , параметризован вектором положения r . В этом случае волновое число k , величина k , по-прежнему находится в той же зависимости от длины волны, как показано выше, причем v интерпретируется как скалярная скорость в направлении волнового вектора. Первая форма, использующая обратную длину волны в фазе, не так легко обобщается на волну в произвольном направлении.

Также распространены обобщения на синусоиды других фаз и на сложные экспоненты; см . плоская волна . Типичное соглашение об использовании фазы косинуса вместо фазы синуса при описании волны основано на том факте, что косинус является действительной частью комплексной экспоненты в волне.

$Ae^{i\left(kx-\omega t\right)}.$

Общие СМИ

Длина волны уменьшается в среде с более медленным распространением.

Преломление: при попадании в среду, где ее скорость ниже, волна меняет направление.

Разделение цветов призмой (нажмите, чтобы увидеть анимацию, если она еще не воспроизводится)

Скорость волны зависит от среды, в которой она распространяется. В частности, скорость света в среде меньше, чем в вакууме , а это означает, что той же частоте будет соответствовать более короткая длина волны в среде, чем в вакууме, как показано на рисунке справа.

Это изменение скорости при входе в среду вызывает преломление или изменение направления волн, которые сталкиваются с границей раздела сред под углом. Для электромагнитных волн это изменение угла распространения регулируется законом Снеллиуса .

Скорость волны в одной среде не только может отличаться от скорости волны в другой, но и обычно зависит от длины волны. В результате изменение направления при входе в другую среду меняется в зависимости от длины волны.

Для электромагнитных волн скорость в среде определяется ее показателем преломления согласно закону

$v={\frac {c}{n(\lambda _{0})}},$

где c — скорость света в вакууме, а n ( λ ₀ ) — показатель преломления среды на длине волны λ ₀ , причем последний измеряется в вакууме, а не в среде. Соответствующая длина волны в среде равна

$\lambda ={\frac {\lambda _{0}}{n(\lambda _{0})}}.$

Когда указываются длины волн электромагнитного излучения, обычно имеется в виду длина волны в вакууме, если только длина волны специально не определена как длина волны в какой-либо другой среде. В акустике, где для существования волн необходима среда, значение длины волны указывается для указанной среды.

Изменение скорости света в зависимости от длины волны известно как дисперсия , и оно также отвечает за известное явление, при котором свет разделяется на составляющие цвета с помощью призмы . Разделение происходит, когда показатель преломления внутри призмы меняется в зависимости от длины волны, поэтому волны разной длины распространяются внутри призмы с разной скоростью, заставляя их преломляться под разными углами. Математическое соотношение, которое описывает, как скорость света в среде зависит от длины волны, известно как дисперсионное соотношение .

Неоднородные среды

Различные локальные длины волн в зависимости от гребня океанской волны, приближающейся к берегу.

Длина волны может быть полезным понятием, даже если волна не является периодической в ​​пространстве. Например, в океанской волне, приближающейся к берегу, как показано на рисунке, находящаяся волна колеблется с различной локальной длиной волны, которая частично зависит от глубины морского дна по сравнению с высотой волны. Анализ волны может быть основан на сравнении местной длины волны с местной глубиной воды.

Синусоидальная волна, бегущая в неоднородной среде с потерями

Волны, синусоидальные во времени, но распространяющиеся в среде, свойства которой меняются в зависимости от положения ( неоднородная среда), могут распространяться со скоростью, меняющейся в зависимости от положения, и, как следствие, не могут быть синусоидальными в пространстве. На рисунке справа показан пример. По мере замедления волны длина волны становится короче, а амплитуда увеличивается; после места максимального отклика короткая длина волны связана с большими потерями и волна затухает.

Анализ дифференциальных уравнений таких систем часто проводится приближенно с использованием метода ВКБ (также известного как метод Лиувилля – Грина ). Этот метод интегрирует фазу в пространстве, используя локальное волновое число , которое можно интерпретировать как указание «локальной длины волны» решения как функции времени и пространства. Этот метод рассматривает систему локально, как если бы она была однородной с локальными свойствами; в частности, локальная скорость волны, связанная с частотой, — это единственное, что необходимо для оценки соответствующего локального волнового числа или длины волны. Кроме того, метод вычисляет медленно меняющуюся амплитуду, чтобы удовлетворить другие ограничения уравнений или физической системы, например, сохранение энергии в волне.

Кристаллы

Волну на линии а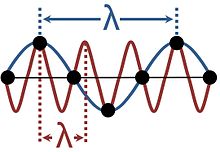томов можно интерпретировать в соответствии с различными длинами волн.

Волны в кристаллических твердых телах не являются непрерывными, поскольку состоят из колебаний дискретных частиц, расположенных в регулярной решетке. Это приводит к наложению спектров, поскольку можно считать, что одна и та же вибрация имеет разные длины волн, как показано на рисунке. Описания с использованием более чем одной из этих длин волн являются излишними; принято выбирать самую длинную длину волны, соответствующую данному явлению. Диапазон длин волн, достаточный для описания всех возможных волн в кристаллической среде, соответствует волновым векторам, приуроченным к зоне Бриллюэна .

Эта неопределенность длины волны в твердых телах важна при анализе волновых явлений, таких как энергетические зоны и колебания решетки . Это математически эквивалентно наложению псевдонимов сигнала, который дискретизируется через дискретные промежутки времени.

Более общие формы сигналов

Почти периодические волны на мелководье

Понятие длины волны чаще всего применяется к синусоидальным или почти синусоидальным волнам, поскольку в линейной системе синусоида представляет собой уникальную форму, которая распространяется без изменения формы – только с изменением фазы и, возможно, с изменением амплитуды. Длина волны (или, альтернативно, волновое число или волновой вектор ) является характеристикой волны в пространстве, которая функционально связана с ее частотой, ограниченной физикой системы. Синусоиды — это простейшие решения бегущей волны , а более сложные решения можно построить с помощью суперпозиции .

В частном случае бездисперсионных и однородных сред волны, отличные от синусоиды, распространяются с неизменной формой и постоянной скоростью. В определенных обстоятельствах волны неизменной формы могут возникать и в нелинейных средах; например, на рисунке показаны океанские волны на мелководье, имеющие более острые гребни и более пологие впадины, чем у синусоиды, типичной для кноидальной волны , бегущая волна, названная так потому, что она описывается эллиптической функцией Якоби - го m порядка, обычно обозначаемой как cn ( x ; m ) . большой амплитуды Океанские волны определенной формы могут распространяться без изменений из-за свойств нелинейной среды поверхностных волн.

Длина волны периодической, но несинусоидальной формы.

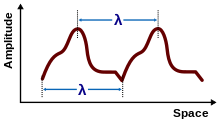
Если бегущая волна имеет фиксированную форму, повторяющуюся в пространстве или во времени, то это периодическая волна . Иногда считается, что такие волны имеют длину волны, даже если они не синусоидальные. Как показано на рисунке, длина волны измеряется между последовательными соответствующими точками на форме сигнала.

Волновые пакеты

Распространяющийся волновой пакет

Основная статья: Волновой пакет

Локализованные волновые пакеты , «всплески» волнового действия, когда каждый волновой пакет распространяется как единое целое, находят применение во многих областях физики. Волновой пакет имеет огибающую , которая описывает общую амплитуду волны; внутри конверта расстояние между соседними пиками или впадинами иногда называют локальной длиной волны . Пример показан на рисунке. В общем, огибающая волнового пакета движется со скоростью, отличной от скорости составляющих его волн.

Используя анализ Фурье , волновые пакеты можно анализировать на бесконечные суммы (или интегралы) синусоидальных волн с разными волновыми числами или длинами волн.

Луи де Бройль постулировал, что все частицы с определенным значением импульса p имеют длину волны λ = h/p , где h — постоянная Планка . Эта гипотеза легла в основу квантовой механики . В настоящее время эта длина волны называется длиной волны де Бройля . Например, электроны в ЭЛТ- дисплее имеют длину волны де Бройля около 10 ⁻¹³ м. Чтобы предотвратить распространение волновой функции такой частицы по всему пространству, де Бройль предложил использовать волновые пакеты для представления частиц, локализованных в пространстве. Пространственное распространение волнового пакета и распространение волновых чисел синусоид, составляющих пакет, соответствуют неопределенностям в положении и импульсе частицы, произведение которых ограничено принципом неопределенности Гейзенберга .

Интерференция и дифракция

Двухщелевая интерференция

Основная статья: Интерференция (распространение волн)

Картина интенсивности света на экране для света, проходящего через две щели. Метки справа относятся к разнице длин путей от двух щелей, которые здесь идеализированы как точечные источники.

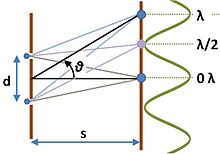
Когда синусоидальные сигналы суммируются, они могут усиливать друг друга (конструктивная интерференция) или нейтрализовать друг друга (деструктивная интерференция) в зависимости от их относительной фазы. Это явление используется в интерферометре . Простой пример — эксперимент Юнга , в котором свет пропускают через две щели . Как показано на рисунке, свет проходит через две щели и попадает на экран. Путь света к положению на экране различен для двух щелей и зависит от угла θ, который этот путь образует с экраном. Если мы предположим, что экран находится достаточно далеко от щелей (т. е. s велико по сравнению с расстоянием между щелями d ), то пути почти параллельны, а разность путей равна просто d sin θ. Соответственно, условием конструктивного вмешательства является:

$d\sin \theta =m\lambda \ ,$

где m — целое число, а для деструктивного вмешательства:

$d\sin \theta =(m+1/2)\lambda \ .$

Таким образом, если известна длина волны света, расстояние между щелями можно определить по интерференционной картине или полосам , и наоборот .

Для нескольких прорезей шаблон

$I_{q}=I_{1}\sin ^{2}\left({\frac {q\pi g\sin \alpha }{\lambda }}\right)/\sin ^{2}\left({\frac {\pi g\sin \alpha }{\lambda }}\right)\ ,$

где q — количество щелей, а g — постоянная решетки. Первый фактор, I ₁ , представляет собой результат для одной щели, который модулирует более быстро меняющийся второй фактор, который зависит от количества щелей и расстояния между ними. На рисунке I ₁ установлен в единицу, что является очень грубым приближением.

Эффект интерференции заключается в перераспределении света, поэтому энергия, содержащаяся в свете, не изменяется именно там, где она проявляется.

Однощелевая дифракция

Основные статьи: Дифракция и дифракционный формализм

Дифракционная картина двойной щели имеет однощелевую огибающую .

Понятие разности хода и конструктивной или деструктивной интерференции, использованное выше для эксперимента с двумя щелями, применимо также к отображению единственной щели света, перехваченной на экране. Основным результатом этой интерференции является распространение света из узкой щели на более широкое изображение на экране. Такое распределение волновой энергии называется дифракцией .

В зависимости от расстояния между источником и экраном различают два типа дифракции: дифракция Фраунгофера или дифракция в дальнем поле при больших расстояниях и дифракция Френеля или дифракция в ближнем поле при близких расстояниях.

При анализе одиночной щели учитывается ненулевая ширина щели, и каждая точка апертуры принимается за источник одного вклада в пучок света ( вейвлеты Гюйгенса ). На экране свет, приходящий из каждой позиции внутри щели, имеет разную длину пути, хотя, возможно, и очень небольшую разницу. Следовательно, возникают помехи.

На дифракционной картине Фраунгофера, достаточно далекой от единственной щели, в приближении малых углов разброс интенсивности S связан с положением x через квадрат функции sinc :

$S(u)=\mathrm {sinc} ^{2}(u)=\left({\frac {\sin \pi u}{\pi u}}\right)^{2}\ ;$ с $u={\frac {xL}{\lambda R}}\ ,$

где L — ширина щели, R — расстояние рисунка (на экране) от щели, а λ — длина волны используемого света. Функция S имеет нули, где u — ненулевое целое число, где находятся значения x с расстоянием, пропорциональным длине волны.

Разрешение, ограниченное дифракцией

Основные статьи: Угловое разрешение и система с ограничением дифракции

Дифракция является фундаментальным ограничением разрешающей способности оптических инструментов, таких как телескопы (включая радиотелескопы ) и микроскопы . Для круглой апертуры пятно изображения, ограниченное дифракцией, известно как диск Эйри ; расстояние x в формуле однощелевой дифракции заменяется радиальным расстоянием r , а синус заменяется на 2 J ₁ , где J ₁ первого порядка — функция Бесселя .

Разрешимый пространственный размер объектов, рассматриваемых через микроскоп, ограничен согласно критерию Рэлея , радиусу до первого нуля диска Эйри, размером, пропорциональным длине волны используемого света и зависящему от числовой апертуры :

$r_{Airy}=1.22{\frac {\lambda }{2\mathrm {NA} }}\ ,$

где числовая апертура определяется как $\mathrm {NA} =n\sin \theta \;$ где θ — половина угла конуса лучей, воспринимаемых объективом микроскопа .

Угловой : размер центральной яркой части (радиус до первого нуля диска Эйри ) изображения, дифрагированного круглой апертурой, мера, наиболее часто используемая для телескопов и камер, составляет

$\delta =1.22{\frac {\lambda }{D}}\ ,$

где λ — длина волны, фокусируемой для формирования изображения, D — диаметр входного зрачка системы формирования изображений, в тех же единицах, а угловое разрешение δ — в радианах.

Как и в случае с другими дифракционными картинами, картина масштабируется пропорционально длине волны, поэтому более короткие длины волн могут привести к более высокому разрешению.

субволновая длина

Термин «субволновая длина» используется для описания объекта, имеющего одно или несколько измерений меньше длины волны, с которой объект взаимодействует. Например, термин « оптическое волокно субволнового диаметра» означает оптическое волокно , диаметр которого меньше длины волны света, распространяющегося через него.

Субволновая частица — это частица размером меньше длины волны света, с которым она взаимодействует (см. Рэлеевское рассеяние ). Субволновые апертуры представляют собой отверстия размером меньше длины волны света, распространяющегося через них. Такие структуры находят применение в необычной оптической передаче , волноводах с нулевой модой , а также в других областях фотоники .

Субволновая длина может также относиться к явлению, связанному с объектами субволновой длины; например, субволновая визуализация .

Угловая длина волны

Связь между длиной волны, угловой длиной волны и другими свойствами волны.

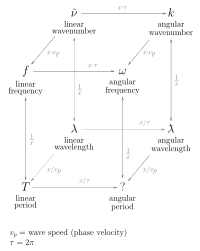
Величиной, связанной с длиной волны, является угловая длина волны (также известная как приведенная длина волны ), обычно обозначаемая ƛ («лямбда-бар» или лямбда с перемычкой ). Она равна обычной длине волны, уменьшенной в 2π раз ( ƛ = λ /2π ), в единицах СИ - метр на радиан. Это обратное угловому волновому числу ( k = 2π/ λ ). Обычно он встречается в квантовой механике, где используется в сочетании с приведенной постоянной Планка (символ ħ , h-бар) и угловой частотой (символ ω = 2π f ).

См. также

• Спектр излучения
• Конверт (волны)
• Линии Фраунгофера - темные линии в солнечном спектре, традиционно используемые в качестве эталонных оптических длин волн.
• Указатель волновых статей
• Измерение длины
• Спектральная линия
• Спектроскопия
• Спектр

Внешние ссылки

• Преобразование: длина волны в частоту и наоборот – звуковые волны и радиоволны.
• Учебный ресурс по звуку, включая длину волны, для 14–16 лет. Архивировано 13 марта 2012 г. в Wayback Machine.
• Видимый электромагнитный спектр отображается в веб-цветах с соответствующими длинами волн.