Метод группы перенормировки кривизны

В теоретической физике метод перенормировочной группы кривизны (CRG) представляет собой аналитический подход к определению фазовых границ и критического поведения топологических систем . Топологические фазы — это фазы материи, которые появляются в некоторых квантово-механических системах при нулевой температуре из-за сильного вырождения волновой основного состояния функции . Они называются топологическими, потому что могут быть описаны различными (дискретными) значениями нелокального топологического инварианта . Это контрастирует с нетопологическими фазами материи (например, ферромагнетизмом ), которые могут быть описаны различными значениями локального параметра порядка . Состояния с разными значениями топологического инварианта не могут переходить друг в друга без фазового перехода . Топологический инвариант строится на основе функции кривизны, которую можно вычислить по объемному гамильтониану системы. При фазовом переходе функция кривизны расходится, и топологический инвариант соответственно скачкообразно перескакивает от одного значения к другому. Метод CRG работает путем обнаружения расхождения в функции кривизны и, таким образом, определения границ между различными топологическими фазами. Кроме того, из расхождения функции кривизны извлекается законы масштабирования , которые описывают критическое поведение, т.е. как различные величины (такие как восприимчивость или длина корреляции ) ведут себя при приближении к топологическому фазовому переходу. Метод CRG был успешно применен к множеству статических, периодически управляемых, слабо и сильно взаимодействующих систем для классификации природы соответствующих топологических фазовых переходов.

Фон

Топологические фазы — это квантовые фазы материи , которые характеризуются устойчивым вырождением основного состояния и квантованными геометрическими фазами . Переходы между различными топологическими фазами обычно называют топологическими фазовыми переходами, которые характеризуются дискретными скачками топологического инварианта. ${\mathcal {C}}$. При настройке одного или нескольких параметров системы $\mathbf {M} =(\mathbf {M} _{1},\mathbf {M} _{2},\dots )$, ${\mathcal {C}}$ резко скачет от одного целого числа к другому в критической точке $\mathbf {M} _{c}$. Обычно топологический инвариант ${\mathcal {C}}$ принимает форму интегрирования функции кривизны $F(\mathbf {k} )$ в импульсном пространстве :

Продолжительность: 14 секунд. 0:14

Поведение функции кривизны (связность Берри) для модели Китаева (верхняя панель) в зависимости от изменения параметра в пространстве параметров (нижняя панель). Вертикальные красные линии изображают топологические границы фаз. При топологических фазовых переходах связность Берри расходится и меняет знак вокруг точек высокой симметрии k = 0.

$${\mathcal {C}}=\int \mathrm {d} ^{D}k\,\,F(\mathbf {k} ,{\bf {M}}).$$В зависимости от размерности и симметрии системы функция кривизны может быть связностью Берри , кривизной Берри или более сложным объектом.

Вблизи точек высокой симметрии ${\bf {k}}_{0}={\bf {k}}_{0}+{\bf {G}}$ в $D$-мерное импульсное пространство, где ${\bf {G}}$ — вектор обратной решетки , функция кривизны обычно имеет лоренцеву форму. $$F({\bf {k}}_{0}+\delta {\bf {k}},{\bf {M}})={\frac {F({\bf {k}}_{0},{\bf {M}})}{1+\xi ^{2}\delta k^{2}}}\,,$$где $1/\xi$ определяет ширину многомерного пика. Приближаемся к критической точке ${\bf {M}}\rightarrow {\bf {M}}_{c}$ пик постепенно расходится, меняя знак перехода: $$\lim _{\mathbf {M} \rightarrow \mathbf {M} _{c}^{+}}F(\mathbf {k} _{0},\mathbf {M} )=-\lim _{\mathbf {M} \rightarrow \mathbf {M} _{c}^{-}}F(\mathbf {k} _{0},\mathbf {M} )=\pm \infty ,\;\;\lim _{\mathbf {M} \rightarrow \mathbf {M} _{c}}\xi =\infty \;,$$Такое поведение показано на видео сбоку к делу $D=1$.

Законы масштабирования, критические показатели и универсальность

Дивергенция функции кривизны позволяет определить критические показатели степени. $\gamma ,\nu$ как $$|F({\bf {k}}_{0},{\bf {M}})|\propto |{\bf {M}}-{\bf {M}}_{c}|^{-\gamma },\;\;\;\;\;\xi \propto |{\bf {M}}-{\bf {M}}_{c}|^{-\nu }.$$ Сохранение топологического инварианта ${\mathcal {C}}=\mathrm {const.}$, когда переход приближается с той или иной стороны, дает закон масштабирования , который ограничивает показатели степени $$\gamma =D\nu ,$$ где $D$ размерность задачи. Эти показатели служат для классификации топологических фазовых переходов по различным классам универсальности .

Чтобы экспериментально измерить критические показатели степени, необходимо иметь доступ к функции кривизны с определенным уровнем точности. Хорошими кандидатами в настоящее время являются квантово-инженерная фотоника и ультрахолодные атомные системы. В первом случае функцию кривизны можно извлечь из аномального смещения волновых пакетов при оптической импульсной накачке в связанных петлях волокна. Для ультрахолодных атомов в оптических решетках кривизна Берри может быть достигнута за счет квантовой интерференции. или измерения скорости волнового пакета, вызванные силой.

Корреляционная функция

функции Преобразование Фурье кривизны $${\tilde {F}}({\bf {R}})=\int {\frac {d^{D}{\bf {k}}}{(2\pi )^{D}}}\;e^{i{\bf {k}}\cdot {\bf {R}}}\;F({\bf {k}},M)$$ обычно измеряет перекрытие определенных квантово-механических волновых функций или более сложных объектов, и поэтому она интерпретируется как корреляционная функция . Например, если функция кривизны представляет собой невзаимодействующую или многочастичную связь Берри или кривизну Берри, корреляционная функция ${\tilde {F}}({\bf {R}})$ является мерой перекрытия функций Ванье, сосредоточенных в двух домашних ячейках, находящихся на расстоянии ${\bf {R}}$ отдельно. Из-за упомянутой выше лоренцевой формы функции кривизны преобразование Фурье функции кривизны затухает с увеличением масштаба длины $\xi$. Следовательно, $\xi$ интерпретируется как длина корреляции, а ее критический показатель присваивается равным $\nu$ как в теории Ландау . Кроме того, длина корреляции связана с длиной локализации топологических краевых состояний , таких как моды Майораны .

Уравнение масштабирования

Процедура масштабирования, идентифицирующая топологические фазовые переходы, основана на дивергенции функции кривизны. Это итерационная процедура, которая для заданного набора параметров ${\bf {M}}$ который управляет топологией, ищет новый набор параметров ${\bf {M}}^{\prime }$ это удовлетворяет $$F({\bf {k}}_{0},{\bf {M}}^{\prime })=F({\bf {k}}_{0}+\delta {\bf {k}},{\bf {M}}),$$где ${\bf {k}}_{0}$ является точкой высокой симметрии и $\delta {\bf {k}}$ небольшое отклонение от него. Эта процедура ищет путь в пространстве параметров ${\bf {M}}$ вдоль которого дивергенция функции кривизны уменьшается, образуя поток ренормгруппы , вытекающий из топологических фазовых переходов. Название «группа перенормировки кривизны» происходит именно от этой процедуры, которая перенормирует профиль функции кривизны. Письмо $\mathrm {d} M_{i}=M_{i}^{\prime }-M_{i}$и $\delta k_{j}^{2}\equiv \mathrm {d} l$и расширение приведенного выше уравнения масштабирования до ведущего порядка дает общее уравнение ренормгруппы

Топологическая фазовая диаграмма периодически управляемой цепи Китаева, полученная методом ренормгруппы кривизны

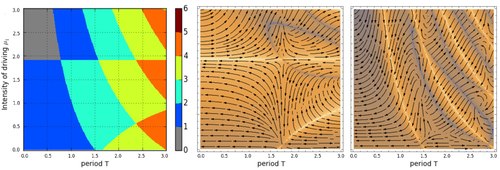
$${\frac {\mathrm {d} M_{i}}{\mathrm {d} l}}={\frac {1}{2}}{\frac {\partial _{k}^{2}F({\bf {k}},{\bf {M}}){\big |}_{k=k_{0}}}{\partial _{M_{i}}F({\bf {k}}_{0},{\bf {M}})}}.$$Поток ренормгруппы можно получить непосредственно как график потока правой части этого дифференциального уравнения . Численно это дифференциальное уравнение требует оценки функции кривизны только при нескольких импульсах. Следовательно, этот метод является очень эффективным способом выявления топологических фазовых переходов, особенно в периодически управляемых системах (также известных как системы Флоке ) и взаимодействующих системах.

См. также

• Топологическое квантовое число
• Соединение ягод и кривизна
• Топологический изолятор
• Периодическая таблица топологических инвариантов
• Дирак имеет значение
• теория Ландау
• Критический показатель
• Закон масштабирования
• Корреляционная функция (статистическая механика)
• Универсальность (динамические системы)
• Ренормгруппа
• Теория Флоке
• Майорановский фермион
• Поверхностные состояния