Распределение Коши

«Распределение Лоренца» перенаправляется сюда. Не путать с кривой Лоренца или системой Лоренца .

Коши

Функция плотности вероятности Фиолетовая кривая представляет собой стандартное распределение Коши.
Кумулятивная функция распределения
Параметры	$x_{0}\!$ местоположение ( реальное ) $\gamma >0$ масштаб (реальный)
Поддерживать	$\displaystyle x\in (-\infty ,+\infty )\!$
PDF	${\frac {1}{\pi \gamma \,\left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}\!$
CDF	${\frac {1}{\pi }}\arctan \left({\frac {x-x_{0}}{\gamma }}\right)+{\frac {1}{2}}\!$
Квантиль	$x_{0}+\gamma \,\tan[\pi (p-{\tfrac {1}{2}})]$
Иметь в виду	неопределенный
медиана	$x_{0}\!$
Режим	$x_{0}\!$
Дисперсия	неопределенный
БЕЗУМНЫЙ	$\gamma$
асимметрия	неопределенный
Избыточный эксцесс	неопределенный
Энтропия	$\log(4\pi \gamma )\!$
МГФ	не существует
CF	$\displaystyle \exp(x_{0}\,i\,t-\gamma \,|t|)\!$
Информация о Фишере	${\frac {1}{2\gamma ^{2}}}$

Распределение Коши , названное в честь Огюстена Коши , представляет собой непрерывное распределение вероятностей . Оно также известно, особенно среди физиков , как распределение Лоренца (по имени Хендрика Лоренца ), распределение Коши–Лоренца , функция Лоренца (иан) или распределение Брейта–Вигнера . Распределение Коши $f(x;x_{0},\gamma )$ - это распределение точки пересечения луча, исходящего из $(x_{0},\gamma )$ с равномерно распределенным углом. Это также распределение отношения двух независимых нормально распределенных случайных величин со средним нулевым значением.

Распределение Коши часто используется в статистике как канонический пример « патологического » распределения, поскольку и его ожидаемое значение , и его дисперсия не определены (но см. § Моменты ниже). Распределение Коши не имеет конечных моментов порядка больше или равного единице; существуют только дробные абсолютные моменты. Распределение Коши не имеет производящей функции момента .

В математике оно тесно связано с ядром Пуассона , которое является фундаментальным решением уравнения Лапласа в верхней полуплоскости .

Это одно из немногих стабильных распределений с функцией плотности вероятности, которую можно выразить аналитически, остальные — нормальное распределение и распределение Леви .

История

Оценка среднего и стандартного отклонения по выборке из распределения Коши (внизу) не сходится по мере увеличения размера выборки, как в случае нормального распределения (вверху). В оценках могут быть сколь угодно большие скачки, как видно на графиках внизу. (Нажмите, чтобы развернуть)

Функция, имеющая форму функции плотности распределения Коши, была геометрически изучена Ферма в 1659 году и позже была известна как ведьма Аньези , после того как Аньези включила ее в качестве примера в свой учебник по исчислению 1748 года. Несмотря на название, первый явный анализ свойств распределения Коши был опубликован французским математиком Пуассоном в 1824 году, а Коши стал ассоциироваться с ним только во время академической полемики в 1853 году. Пуассон отметил, что если взять среднее значение наблюдений, следующих за таким распределением, то средняя ошибка не сходилось ни к какому конечному числу. Таким образом, центральной использование Лапласом предельной теоремы для такого распределения было неуместным, поскольку предполагало конечное среднее значение и дисперсию. Несмотря на это, Пуассон не считал этот вопрос важным, в отличие от Бьенеме , которому предстояло вовлечь Коши в длительный спор по этому поводу.

Конструкции

Вот самые важные конструкции.

Вращательная симметрия

Если кто-то стоит перед линией и бьет по мячу в случайном направлении (точнее, под углом) равномерно и случайно по направлению к линии, то распределение точки, в которой мяч попадает на линию, является распределением Коши.

Более формально, рассмотрим точку $(x_{0},\gamma )$ в плоскости xy и выберите линию, проходящую через точку, с ее направлением (угол с $x$-ось) выбирается равномерно (от -90° до +90°) случайным образом. Пересечение линии с осью X представляет собой распределение Коши с местоположением $x_{0}$ и масштабировать $\gamma$.

Это определение дает простой способ выборки из стандартного распределения Коши. Позволять $u$ быть выборкой из равномерного распределения из $[0,1]$, то мы сможем сгенерировать образец, $x$ из стандартного распределения Коши с использованием

$x=\tan \left(\pi (u-{\frac {1}{2}})\right)$

Когда $U$ и $V$ две независимые нормально распределенные случайные величины с ожидаемым значением 0 и дисперсией 1, тогда отношение $U/V$ имеет стандартное распределение Коши.

В более общем смысле, если $(U,V)$ является вращательно-симметричным распределением на плоскости, то соотношение $U/V$ имеет стандартное распределение Коши.

Функция плотности вероятности (PDF)

Распределение Коши — это распределение вероятностей со следующей функцией плотности вероятности (PDF)

$f(x;x_{0},\gamma )={\frac {1}{\pi \gamma \left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}={1 \over \pi }\left[{\gamma \over (x-x_{0})^{2}+\gamma ^{2}}\right],$

где $x_{0}$ — параметр местоположения , определяющий местоположение пика распределения, и $\gamma$ , параметр масштаба который определяет полуширину на полувысоте (HWHM), альтернативно $2\gamma$ Полная ширина на половине высоты (FWHM). $\gamma$ также равна половине межквартильного размаха и иногда называется вероятной ошибкой . Огюстен-Луи Коши использовал такую ​​функцию плотности в 1827 году с бесконечно малым параметром масштаба, определив то, что сейчас будет называться дельта-функцией Дирака .

Свойства PDF

Максимальное значение или амплитуда PDF Коши составляет ${\frac {1}{\pi \gamma }}$, расположенный по адресу $x=x_{0}$.

Иногда удобно выразить PDF через комплексный параметр $\psi =x_{0}+i\gamma$

$f(x;\psi )={\frac {1}{\pi }}\,{\textrm {Im}}\left({\frac {1}{x-\psi }}\right)={\frac {1}{\pi }}\,{\textrm {Re}}\left({\frac {-i}{x-\psi }}\right)$

Особый случай, когда $x_{0}=0$ и $\gamma =1$ называется стандартным распределением Коши с функцией плотности вероятности

$f(x;0,1)={\frac {1}{\pi (1+x^{2})}}.\!$

В физике часто используется трехпараметрическая функция Лоренца:

$f(x;x_{0},\gamma ,I)={\frac {I}{\left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}=I\left[{\gamma ^{2} \over (x-x_{0})^{2}+\gamma ^{2}}\right],$

где $I$ это высота пика. Указанная трехпараметрическая функция Лоренца, вообще говоря, не является функцией плотности вероятности, поскольку она не интегрируется до 1, за исключением особого случая, когда $I={\frac {1}{\pi \gamma }}.\!$

Кумулятивная функция распределения (CDF)

Распределение Коши — это распределение вероятностей со следующей кумулятивной функцией распределения (CDF):

$F(x;x_{0},\gamma )={\frac {1}{\pi }}\arctan \left({\frac {x-x_{0}}{\gamma }}\right)+{\frac {1}{2}}$

а функция квантиля (обратный cdf ) распределения Коши равна

$Q(p;x_{0},\gamma )=x_{0}+\gamma \,\tan \left[\pi \left(p-{\tfrac {1}{2}}\right)\right].$

Отсюда следует, что первый и третий квартили равны $(x_{0}-\gamma ,x_{0}+\gamma )$, и, следовательно, межквартильный размах равен $2\gamma$.

Для стандартного распределения кумулятивная функция распределения упрощается до функции арктангенса. $\arctan(x)$:

$F(x;0,1)={\frac {1}{\pi }}\arctan \left(x\right)+{\frac {1}{2}}$

Другие конструкции

Стандартное распределение Коши представляет собой Стьюдента t -распределение с одной степенью свободы, поэтому его можно построить любым методом, позволяющим построить t-распределение Стьюдента.

Если $\Sigma$ это $p\times p$ положительно-полуопределенная ковариационная матрица со строго положительными диагональными элементами, то для независимых и одинаково распределенных $X,Y\sim N(0,\Sigma )$ и любое случайное $p$-вектор $w$ независимый от $X$ и $Y$ такой, что $w_{1}+\cdots +w_{p}=1$ и $w_{i}\geq 0,i=1,\ldots ,p,$ (определяя категориальное распределение ) считается, что

$\sum _{j=1}^{p}w_{j}{\frac {X_{j}}{Y_{j}}}\sim \mathrm {Cauchy} (0,1).$

Характеристики

Распределение Коши является примером распределения, для которого не определены среднее значение , дисперсия или более высокие моменты . Его мода и медиана четко определены и равны $x_{0}$.

Распределение Коши — это бесконечно делимое распределение вероятностей . Это также строго стабильный дистрибутив.

Как и все стабильные распределения, семейство масштабов местоположения , к которому принадлежит распределение Коши, замкнуто относительно линейных преобразований с действительными коэффициентами. Кроме того, семейство случайных величин, распределенных Коши, замкнуто относительно дробно-линейных преобразований с вещественными коэффициентами. В этой связи см. также параметризацию распределений Коши МакКаллаха .

Сумма случайных величин, распределенных Коши

Если $X_{1},X_{2},\ldots ,X_{n}$ являются выборкой IID из стандартного распределения Коши, то их выборочное среднее ${\bar {X}}={\frac {1}{n}}\sum _{i}X_{i}$ также является стандартным распределением Коши. В частности, среднее значение не сходится к среднему, и поэтому стандартное распределение Коши не подчиняется закону больших чисел.

Это можно доказать путем повторного интегрирования с PDF или, что более удобно, с помощью характеристической функции стандартного распределения Коши (см. ниже): $$\varphi _{X}(t)=\operatorname {E} \left[e^{iXt}\right]=e^{-|t|}.$$При этом мы имеем $\varphi _{\sum _{i}X_{i}}(t)=e^{-n|t|}$, и так ${\bar {X}}$ имеет стандартное распределение Коши.

В более общем смысле, если $X_{1},X_{2},\ldots ,X_{n}$ независимы и распределены Коши с параметрами местоположения $x_{1},\ldots ,x_{n}$ и весы $\gamma _{1},\ldots ,\gamma _{n}$, и $a_{1},\ldots ,a_{n}$ действительные числа, то $\sum _{i}a_{i}X_{i}$ Распределен ли Коши в зависимости от местоположения $\sum _{i}a_{i}x_{i}$ и масштабировать $\sum _{i}|a_{i}|\gamma _{i}$. Мы видим, что не существует закона больших чисел для любой взвешенной суммы независимых распределений Коши.

Это показывает, что условие конечной дисперсии в центральной предельной теореме нельзя отбросить. Это также пример более обобщенной версии центральной предельной теоремы, характерной для всех устойчивых распределений , частным случаем которых является распределение Коши.

Центральная предельная теорема

Если $X_{1},X_{2},\ldots$ и образец IID с PDF $\rho$ такой, что $\lim _{c\to \infty }{\frac {1}{c}}\int _{-c}^{c}x^{2}\rho (x)\,dx={\frac {2\gamma }{\pi }}$ конечно, но не равно нулю, то ${\frac {1}{n}}\sum _{i=1}^{n}X_{i}$ сходится по распределению к распределению Коши с масштабом $\gamma$.

Характеристическая функция

Позволять $X$ обозначают случайную величину, распределенную Коши. Характеристическая функция распределения Коши определяется выражением

$\varphi _{X}(t)=\operatorname {E} \left[e^{iXt}\right]=\int _{-\infty }^{\infty }f(x;x_{0},\gamma )e^{ixt}\,dx=e^{ix_{0}t-\gamma |t|}.$

что представляет собой преобразование Фурье плотности вероятности. Исходная плотность вероятности может быть выражена через характеристическую функцию, по существу, с помощью обратного преобразования Фурье:

$f(x;x_{0},\gamma )={\frac {1}{2\pi }}\int _{-\infty }^{\infty }\varphi _{X}(t;x_{0},\gamma )e^{-ixt}\,dt\!$

n - й момент распределения — это n- я производная характеристической функции, вычисляемой при $t=0$. Обратите внимание, что характеристическая функция не дифференцируема в начале координат: это соответствует тому, что распределение Коши не имеет четко определенных моментов выше нулевого момента.

Расхождение Кульбака – Лейблера

Расхождение Кульбака – Лейблера между двумя распределениями Коши имеет следующую симметричную формулу в замкнутой форме:

$\mathrm {KL} \left(p_{x_{0,1},\gamma _{1}}:p_{x_{0,2},\gamma _{2}}\right)=\log {\frac {\left(\gamma _{1}+\gamma _{2}\right)^{2}+\left(x_{0,1}-x_{0,2}\right)^{2}}{4\gamma _{1}\gamma _{2}}}.$

Любое f-дивергенция между двумя распределениями Коши симметрична и может быть выражена как функция дивергенции хи-квадрат. выражения в закрытой форме для полной вариации , дивергенции Дженсена-Шеннона , расстояния Хеллингера Доступны и т. д.

Энтропия

Энтропия распределения Коши определяется выражением:

${\begin{aligned}H(\gamma )&=-\int _{-\infty }^{\infty }f(x;x_{0},\gamma )\log(f(x;x_{0},\gamma ))\,dx\\[6pt]&=\log(4\pi \gamma )\end{aligned}}$

Производная функции квантиля , функции плотности квантиля, для распределения Коши:

$Q'(p;\gamma )=\gamma \,\pi \,{\sec }^{2}\left[\pi \left(p-{\tfrac {1}{2}}\right)\right].\!$

Дифференциальная энтропия распределения может быть определена через его квантильную плотность: конкретно:

$H(\gamma )=\int _{0}^{1}\log \,(Q'(p;\gamma ))\,\mathrm {d} p=\log(4\pi \gamma )$

Распределение Коши - это распределение вероятностей максимальной энтропии для случайной величины. $X$ для чего

$\operatorname {E} [\log(1+(X-x_{0})^{2}/\gamma ^{2})]=\log 4$

Моменты

Распределение Коши обычно используется в качестве наглядного контрпримера в курсах элементарных вероятностей как распределение без четко определенных (или «неопределенных») моментов.

Примеры моментов

Если мы возьмем образец IID $X_{1},X_{2},\ldots$ из стандартного распределения Коши, то последовательность их выборочного среднего равна $S_{n}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}$, который также имеет стандартное распределение Коши. Следовательно, сколько бы членов мы ни взяли, выборочное среднее не сходится.

Аналогично, выборочная дисперсия $V_{n}={\frac {1}{n}}\sum _{i=1}^{n}(X_{i}-S_{n})^{2}$ тоже не сходится.

Типичная траектория выборочных средних выглядит как длительные периоды медленного стремления к нулю, перемежающиеся большими скачками от нуля, но никогда не уходящие слишком далеко. Типичная траектория выборочных дисперсий выглядит аналогично, но скачки накапливаются быстрее, чем затухание, расходясь к бесконечности.

Типичная траектория $S_{1},S_{2},...$ выглядит как длительные периоды медленного сближения к нулю, перемежающиеся большими скачками от нуля, но никогда не уходящие слишком далеко. Типичная траектория $V_{1},V_{2},...$ выглядит аналогично, но скачки накапливаются быстрее, чем затухание, расходясь в бесконечность. Эти два вида траекторий изображены на рисунке.

Моменты выборки ниже порядка 1 будут сходиться к нулю. Моменты выборки выше порядка 2 будут расходиться до бесконечности даже быстрее, чем дисперсия выборки.

Иметь в виду

Если распределение вероятностей имеет функцию плотности $f(x)$, то среднее значение, если оно существует, определяется выражением

$$\int _{-\infty }^{\infty }xf(x)\,dx.$$ ( 1 )

Мы можем вычислить этот двусторонний несобственный интеграл , вычислив сумму двух односторонних несобственных интегралов. То есть,

$$\int _{-\infty }^{a}xf(x)\,dx+\int _{a}^{\infty }xf(x)\,dx$$ ( 2 )

для произвольного действительного числа $a$.

Чтобы интеграл существовал (даже как бесконечное значение), хотя бы одно из слагаемых этой суммы должно быть конечным, либо оба должны быть бесконечными и иметь одинаковый знак. Но в случае распределения Коши оба слагаемых в этой сумме ( 2 ) бесконечны и имеют противоположные знаки. Следовательно, ( 1 ) не определено, а значит, и среднее значение. Когда среднее значение функции распределения вероятностей (PDF) не определено, никто не может вычислить надежное среднее значение по экспериментальным точкам данных, независимо от размера выборки.

Обратите внимание, что главное значение Коши среднего значения распределения Коши равно $$\lim _{a\to \infty }\int _{-a}^{a}xf(x)\,dx$$что равно нулю. С другой стороны, соответствующий интеграл $$\lim _{a\to \infty }\int _{-2a}^{a}xf(x)\,dx$$ нулю не равно , как можно увидеть, вычислив интеграл. Это еще раз показывает, что среднее значение ( 1 ) не может существовать.

Различные результаты теории вероятностей об ожидаемых значениях , такие как сильный закон больших чисел , не справедливы для распределения Коши.

Меньшие моменты

Абсолютные моменты для $p\in (-1,1)$ определены.Для $X\sim \mathrm {Cauchy} (0,\gamma )$ у нас есть

$\operatorname {E} [|X|^{p}]=\gamma ^{p}\mathrm {sec} (\pi p/2).$

Высшие моменты

Распределение Коши не имеет конечных моментов любого порядка. Некоторые из высших необработанных моментов действительно существуют и имеют значение бесконечности, например, необработанный второй момент:

${\begin{aligned}\operatorname {E} [X^{2}]&\propto \int _{-\infty }^{\infty }{\frac {x^{2}}{1+x^{2}}}\,dx=\int _{-\infty }^{\infty }1-{\frac {1}{1+x^{2}}}\,dx\\[8pt]&=\int _{-\infty }^{\infty }dx-\int _{-\infty }^{\infty }{\frac {1}{1+x^{2}}}\,dx=\int _{-\infty }^{\infty }dx-\pi =\infty .\end{aligned}}$

Переставив формулу, можно увидеть, что второй момент по сути представляет собой бесконечный интеграл от константы (здесь 1). Необработанные моменты с более высокой равномерной мощностью также будут оцениваться до бесконечности. Однако сырые моменты с нечетной силой не определены, что заметно отличается от существования со значением бесконечности. Нечетные исходные моменты не определены, поскольку их значения по существу эквивалентны $\infty -\infty$ поскольку обе половины интеграла расходятся и имеют противоположные знаки. Первый необработанный момент — это среднее значение, которое, будучи странным, не существует. (См. также обсуждение этого вопроса выше.) Это, в свою очередь, означает, что все центральные моменты и стандартизированные моменты не определены, поскольку все они основаны на среднем значении. Дисперсия, которая является вторым центральным моментом, также не существует (несмотря на то, что исходный второй момент существует со значением бесконечности).

Результаты для более высоких моментов следуют из неравенства Гёльдера , которое означает, что более высокие моменты (или половины моментов) расходятся, если это делают более низкие.

Моменты усеченных распределений

Рассмотрим усеченное распределение , определенное путем ограничения стандартного распределения Коши интервалом [−10 ¹⁰⁰ , 10 ¹⁰⁰ ] . Такое усеченное распределение имеет все моменты (и центральная предельная теорема применима к наблюдениям из него); однако почти во всех практических целях оно ведет себя как распределение Коши.

Оценка параметров

Поскольку параметры распределения Коши не соответствуют среднему значению и дисперсии, попытка оценить параметры распределения Коши с использованием выборочного среднего и выборочной дисперсии не увенчается успехом. Например, если выборка iid размером n берется из распределения Коши, среднее значение выборки можно вычислить как:

${\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}$

Хотя выборочные значения $x_{i}$ будет сконцентрировано вокруг центрального значения $x_{0}$, среднее значение выборки будет становиться все более изменчивым по мере увеличения количества наблюдений из-за увеличения вероятности встретить точки выборки с большим абсолютным значением. Фактически распределение выборочного среднего будет равно распределению самих наблюдений; т. е. выборочное среднее большой выборки не лучше (или хуже) оценки $x_{0}$ чем любое отдельное наблюдение из выборки. Аналогичным образом, вычисление выборочной дисперсии приведет к тому, что значения будут увеличиваться по мере увеличения количества наблюдений.

Следовательно, более надежные способы оценки центрального значения $x_{0}$ и параметр масштабирования $\gamma$ необходимы. Один простой метод — принять медианное значение выборки в качестве оценки $x_{0}$ выборки и половина межквартильного размаха в качестве оценки $\gamma$. Были разработаны другие, более точные и надежные методы. Например, усеченное среднее средних 24% статистики порядка выборки дает оценку $x_{0}$ это более эффективно, чем использование выборочной медианы или полного выборочного среднего значения. Однако из-за « толстых хвостов » распределения Коши эффективность оценки снижается, если используется более 24% выборки.

Максимальное правдоподобие также можно использовать для оценки параметров. $x_{0}$ и $\gamma$. Однако это имеет тенденцию усложняться тем фактом, что для этого требуется найти корни полинома высокой степени, и может быть несколько корней, которые представляют локальные максимумы. Кроме того, хотя оценка максимального правдоподобия асимптотически эффективна, она относительно неэффективна для небольших выборок. Логарифмическая функция правдоподобия для распределения Коши для размера выборки $n$ является:

${\hat {\ell }}(x_{1},\dotsc ,x_{n}\mid \!x_{0},\gamma )=-n\log(\gamma \pi )-\sum _{i=1}^{n}\log \left(1+\left({\frac {x_{i}-x_{0}}{\gamma }}\right)^{2}\right)$

Максимизация логарифмической функции правдоподобия по отношению к $x_{0}$ и $\gamma$ взяв первую производную, получим следующую систему уравнений:

${\frac {d\ell }{dx_{0}}}=\sum _{i=1}^{n}{\frac {2(x_{i}-x_{0})}{\gamma ^{2}+\left(x_{i}-\!x_{0}\right)^{2}}}=0$

${\frac {d\ell }{d\gamma }}=\sum _{i=1}^{n}{\frac {2\left(x_{i}-x_{0}\right)^{2}}{\gamma (\gamma ^{2}+\left(x_{i}-x_{0}\right)^{2})}}-{\frac {n}{\gamma }}=0$

Обратите внимание, что

$\sum _{i=1}^{n}{\frac {\left(x_{i}-x_{0}\right)^{2}}{\gamma ^{2}+\left(x_{i}-x_{0}\right)^{2}}}$

является монотонной функцией $\gamma$ и что решение $\gamma$ должен удовлетворить

$\min |x_{i}-x_{0}|\leq \gamma \leq \max |x_{i}-x_{0}|.$

Решение только для $x_{0}$ требуется решить многочлен степени $2n-1$, и решение только для $\,\!\gamma$ требуется решить многочлен степени $2n$. Следовательно, независимо от того, решаете ли вы один параметр или оба параметра одновременно, обычно требуется численное решение на компьютере. Преимущество оценки максимального правдоподобия заключается в асимптотической эффективности; оценка $x_{0}$ использование выборочной медианы асимптотически эффективно лишь на 81% по сравнению с оценкой $x_{0}$ по максимальной вероятности. Усеченное выборочное среднее с использованием статистики среднего порядка 24% составляет около 88% как асимптотически эффективная оценка $x_{0}$ как оценка максимального правдоподобия. Когда метод Ньютона используется для поиска решения для оценки максимального правдоподобия, статистика среднего порядка 24% может использоваться в качестве начального решения для $x_{0}$.

Форму можно оценить с помощью медианы абсолютных значений, поскольку для местоположения 0 переменные Коши $X\sim \mathrm {Cauchy} (0,\gamma )$, $\operatorname {median} (|X|)=\gamma$ параметр формы.

Многомерное распределение Коши

вектор Случайный $X=(X_{1},\ldots ,X_{k})^{T}$ Говорят, что оно имеет многомерное распределение Коши, если каждая линейная комбинация его компонентов $Y=a_{1}X_{1}+\cdots +a_{k}X_{k}$ имеет распределение Коши. То есть для любого постоянного вектора $a\in \mathbb {R} ^{k}$, случайная величина $Y=a^{T}X$ должно иметь одномерное распределение Коши. Характеристическая функция многомерного распределения Коши определяется выражением:

$\varphi _{X}(t)=e^{ix_{0}(t)-\gamma (t)},\!$

где $x_{0}(t)$ и $\gamma (t)$ являются действительными функциями с $x_{0}(t)$ однородная функция первой степени и $\gamma (t)$ положительная однородная функция первой степени. Более формально:

$x_{0}(at)=ax_{0}(t),$

$\gamma (at)=|a|\gamma (t),$

для всех $t$.

Пример двумерного распределения Коши может быть представлен следующим образом:

$f(x,y;x_{0},y_{0},\gamma )={1 \over 2\pi }\left[{\gamma \over ((x-x_{0})^{2}+(y-y_{0})^{2}+\gamma ^{2})^{3/2}}\right].$

Обратите внимание, что в этом примере, хотя ковариация между $x$ и $y$ 0, $x$ и $y$ не являются статистически независимыми .

Мы также можем написать эту формулу для комплексной переменной. Тогда функция плотности вероятности комплексного Коши равна:

$f(z;z_{0},\gamma )={1 \over 2\pi }\left[{\gamma \over (|z-z_{0}|^{2}+\gamma ^{2})^{3/2}}\right].$

Подобно тому, как стандартное распределение Коши представляет собой t-распределение Стьюдента с одной степенью свободы, многомерная плотность Коши представляет собой многомерное распределение Стьюдента с одной степенью свободы. Плотность $k$ измерение Распределение студентов с одной степенью свободы:

$f({\mathbf {x} };{\mathbf {\mu } },{\mathbf {\Sigma } },k)={\frac {\Gamma \left({\frac {1+k}{2}}\right)}{\Gamma ({\frac {1}{2}})\pi ^{\frac {k}{2}}\left|{\mathbf {\Sigma } }\right|^{\frac {1}{2}}\left[1+({\mathbf {x} }-{\mathbf {\mu } })^{T}{\mathbf {\Sigma } }^{-1}({\mathbf {x} }-{\mathbf {\mu } })\right]^{\frac {1+k}{2}}}}.$

Тогда свойства многомерного распределения Коши являются частными случаями многомерного распределения Стьюдента.

Свойства трансформации

• Если $X\sim \operatorname {Cauchy} (x_{0},\gamma )$ затем $kX+\ell \sim {\textrm {Cauchy}}(x_{0}k+\ell ,\gamma |k|)$
• Если $X\sim \operatorname {Cauchy} (x_{0},\gamma _{0})$ и $Y\sim \operatorname {Cauchy} (x_{1},\gamma _{1})$ независимы, то $X+Y\sim \operatorname {Cauchy} (x_{0}+x_{1},\gamma _{0}+\gamma _{1})$ и $X-Y\sim \operatorname {Cauchy} (x_{0}-x_{1},\gamma _{0}+\gamma _{1})$
• Если $X\sim \operatorname {Cauchy} (0,\gamma )$ затем ${\tfrac {1}{X}}\sim \operatorname {Cauchy} (0,{\tfrac {1}{\gamma }})$
• Параметризация МакКаллахом распределений Коши : Выражение распределения Коши через один комплексный параметр $\psi =x_{0}+i\gamma$, определять $X\sim \operatorname {Cauchy} (\psi )$ означать $X\sim \operatorname {Cauchy} (x_{0},|\gamma |)$. Если $X\sim \operatorname {Cauchy} (\psi )$ затем: $${\frac {aX+b}{cX+d}}\sim \operatorname {Cauchy} \left({\frac {a\psi +b}{c\psi +d}}\right)$$ где $a$, $b$, $c$ и $d$ являются действительными числами.
• Используя то же соглашение, что и выше, если $X\sim \operatorname {Cauchy} (\psi )$ затем: $${\frac {X-i}{X+i}}\sim \operatorname {CCauchy} \left({\frac {\psi -i}{\psi +i}}\right)$$где $\operatorname {CCauchy}$ — круговое распределение Коши .

Мера Леви

Распределение Коши представляет собой устойчивое распределение индекса 1. Представление Леви – Хинчина такого устойчивого распределения параметра $\gamma$ дается, для $X\sim \operatorname {Stable} (\gamma ,0,0)\,$ к:

$\operatorname {E} \left(e^{ixX}\right)=\exp \left(\int _{\mathbb {R} }(e^{ixy}-1)\Pi _{\gamma }(dy)\right)$

где

$\Pi _{\gamma }(dy)=\left(c_{1,\gamma }{\frac {1}{y^{1+\gamma }}}1_{\left\{y>0\right\}}+c_{2,\gamma }{\frac {1}{|y|^{1+\gamma }}}1_{\left\{y<0\right\}}\right)\,dy$

и $c_{1,\gamma },c_{2,\gamma }$ можно выразить явно. В случае $\gamma =1$ распределения Коши имеем $c_{1,\gamma }=c_{2,\gamma }$.

Последнее представление является следствием формулы

$\pi |x|=\operatorname {PV} \int _{\mathbb {R} \smallsetminus \lbrace 0\rbrace }(1-e^{ixy})\,{\frac {dy}{y^{2}}}$

Связанные дистрибутивы

• $\operatorname {Cauchy} (0,1)\sim {\textrm {t}}(\mathrm {df} =1)\,$ Стьюдента Распределение ​
• $\operatorname {Cauchy} (\mu ,\sigma )\sim {\textrm {t}}_{(\mathrm {df} =1)}(\mu ,\sigma )\,$ нестандартизованное Стьюдента распределение
• Если $X,Y\sim {\textrm {N}}(0,1)\,X,Y$ независимый, тогда ${\tfrac {X}{Y}}\sim {\textrm {Cauchy}}(0,1)\,$
• Если $X\sim {\textrm {U}}(0,1)\,$ затем $\tan \left(\pi \left(X-{\tfrac {1}{2}}\right)\right)\sim {\textrm {Cauchy}}(0,1)\,$
• Если $X\sim \operatorname {Log-Cauchy} (0,1)$ затем $\ln(X)\sim {\textrm {Cauchy}}(0,1)$
• Если $X\sim \operatorname {Cauchy} (x_{0},\gamma )$ затем ${\tfrac {1}{X}}\sim \operatorname {Cauchy} \left({\tfrac {x_{0}}{x_{0}^{2}+\gamma ^{2}}},{\tfrac {\gamma }{x_{0}^{2}+\gamma ^{2}}}\right)$
• Распределение Коши является предельным случаем распределения Пирсона 4-го типа.
• Распределение Коши является частным случаем распределения Пирсона 7-го типа.
• Распределение Коши является устойчивым распределением : если $X\sim {\textrm {Stable}}(1,0,\gamma ,\mu )$, затем $X\sim \operatorname {Cauchy} (\mu ,\gamma )$.
• Распределение Коши является сингулярным пределом гиперболического распределения.
• Обернутое распределение Коши , принимающее значения по кругу, получается из распределения Коши путем его обертывания вокруг круга.
• Если $X\sim {\textrm {N}}(0,1)$, $Z\sim \operatorname {Inverse-Gamma} (1/2,s^{2}/2)$, затем $Y=\mu +X{\sqrt {Z}}\sim \operatorname {Cauchy} (\mu ,s)$. Для распределений полукоши соотношение сохраняется, если положить $X\sim {\textrm {N}}(0,1)I\{X\geq 0\}$.

Релятивистское распределение Брейта – Вигнера

Основная статья: Релятивистское распределение Брейта – Вигнера

В ядра и физике элементарных частиц энергетический профиль резонанса описывается релятивистским распределением Брейта-Вигнера , а распределение Коши является (нерелятивистским) распределением Брейта-Вигнера.

Возникновение и применение

• В спектроскопии распределение Коши описывает форму спектральных линий , которые подвержены однородному уширению , при котором все атомы взаимодействуют одинаковым образом с частотным диапазоном, содержащимся в форме линии. Многие механизмы вызывают однородное уширение, в первую очередь столкновительное уширение . Время жизни или естественное уширение также приводит к форме линии, описываемой распределением Коши.
• Приложения распределения Коши или его преобразования можно найти в областях, работающих с экспоненциальным ростом . Статья Уайта 1958 года. получили тестовую статистику для оценок ${\hat {\beta }}$ для уравнения $x_{t+1}=\beta {x}_{t}+\varepsilon _{t+1},\beta >1$ и где оценка максимального правдоподобия находится с использованием обычного метода наименьших квадратов, показано, что выборочное распределение статистики представляет собой распределение Коши.

Подобрано кумулятивное распределение Коши для максимального количества осадков за один день с помощью CumFreq , см. также подбор распределения.

• Распределение Коши часто представляет собой распределение наблюдений за вращающимися объектами. Классическая ссылка на это называется проблемой маяка чайки. и, как указано в предыдущем разделе, как распределение Брейта – Вигнера в физике элементарных частиц.
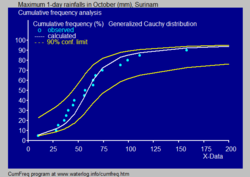
• В гидрологии распределение Коши применяется к экстремальным явлениям, таким как годовое максимальное количество осадков за один день и речной сток. Синее изображение иллюстрирует пример подбора распределения Коши к ранжированному максимальному месячному количеству осадков за один день, а также 90% доверительный интервал, основанный на биномиальном распределении . Данные об осадках представлены в виде координат на графике в рамках кумулятивного частотного анализа .
• Выражение для мнимой части комплексной электрической проницаемости согласно модели Лоренца представляет собой распределение Коши.
• В качестве дополнительного распределения для моделирования «толстых хвостов» в вычислительных финансах распределения Коши могут использоваться для моделирования VAR ( стоимость под риском ), создавая гораздо большую вероятность экстремального риска, чем распределение Гаусса .

См. также

• Полет Леви и процесс Леви
• Распределение Лапласа , преобразование Фурье распределения Коши
• Процесс Коши
• Стабильный процесс
• Слэш-распределение

Внешние ссылки

• «Распределение Коши» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Самое раннее использование: запись о распространении Коши содержит некоторую историческую информацию.
• Вайсштейн, Эрик В. «Распределение Коши» . Математический мир .
• Научная библиотека GNU – Справочное руководство
• Отношения нормальных переменных Джорджа Марсалья