Список квантовых логических вентилей
В квантовых вычислениях на основе вентилей различные наборы квантовых логических вентилей для выражения квантовых операций обычно используются . В следующих таблицах перечислены несколько унитарных квантовых логических элементов, а также их общее название, способы их представления и некоторые их свойства. Управляемые или сопряженные транспонированные ( сопряженные ) версии некоторых из этих вентилей могут не быть перечислены.
Идентификационные ворота и глобальная фаза
[ редактировать ]| Имя | # кубитов | Символ оператора | Матрица | Принципиальная схема | Характеристики | Ссылки |
|---|---|---|---|---|---|---|
| Личность, бездействующий | 1 (любой) | , 𝟙 |  или | [1] | ||
| Глобальная фаза | 1 (любой) | , или |
| [1] |
Идентификационные ворота — это операция идентификации. В большинстве случаев этот элемент не указывается на принципиальных схемах, но он полезен при описании математических результатов.
Это было описано как «цикл ожидания». [2] и НОП . [3] [1]
Глобальные фазовые ворота вводят глобальную фазу ко всему квантовому состоянию кубита. Квантовое состояние однозначно определяется с точностью до фазы. Согласно правилу Борна , фазовый коэффициент не влияет на результат измерения : для любого .
Потому что когда глобальный фазовый вентиль применяется к одному кубиту в квантовом регистре , глобальная фаза всего регистра изменяется.
Также,
Эти ворота могут быть расширены до любого количества кубитов или кудитов .
Кубитные ворота Клиффорда
[ редактировать ]В эту таблицу включены часто используемые вентили Клиффорда для кубитов. [1] [4] [5]
| Имена | # кубитов | Символ оператора | Матрица | Принципиальная схема | Некоторые свойства | Ссылки |
|---|---|---|---|---|---|---|
| Pauli XПаули НЕТ, немного перевернуть | 1 |
| [1] [6] | |||
| Паули Ю | 1 |  |
| [1] [6] | ||
| Паула З , переворот фазы | 1 |  |
| [1] [6] | ||
| Фазовый вентиль S , квадратный корень из Z | 1 |  | [1] [6] | |||
| Квадратный корень из X , квадратный корень из НЕ | 1 | , , |  | [1] [7] | ||
| Адамар , Уолш-Адамар | 1 |  |
| [1] [6] | ||
| Контролируется НЕ , контролируемый- X , управляемый битовый переворот, обратимый исключительный ИЛИ , Фейнман | 2 | , |  |
Выполнение: | [1] [6] | |
| Антиконтролируемый-НЕ, антиконтролируемый - X , нулевой контроль, управление-0-НЕ, обратимый эксклюзивный NOR | 2 | , , |  |
| [1] | |
| Контролируемый- Z , управляемый переворот знака, управляемый переворот фазы | 2 | , , , |  |
Выполнение:
| [1] [6] | |
| НЕ с двойным контролем | 2 | 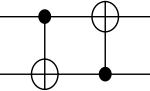 | [8] | |||
| Менять | 2 |  или  |
| [1] [6] | ||
| Воображаемый обмен | 2 |  или  |
| [1] |
Другие ворота Клиффорда, в том числе более многомерные, сюда не включены, но по определению могут быть созданы с помощью и .
Обратите внимание, что если вентиль Клиффорда A не входит в группу Паули, или контролируемый- А не находится в воротах Клиффорда. [ нужна ссылка ]
Набор Клиффорда не является универсальным набором квантовых вентилей.
Неклиффордовские кубитные ворота
[ редактировать ]Относительные фазовые ворота
[ редактировать ]| Имена | # кубитов | Символ оператора | Матрица | Принципиальная схема | Характеристики | Ссылки |
|---|---|---|---|---|---|---|
| Фазовый сдвиг | 1 |  |
| [9] [10] [11] | ||
| Фазовый вентиль Т, п/8 ворота, четвертый корень из Z | 1 | или | 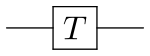 | [1] [6] | ||
| Контролируемая фаза | 2 |  |
Выполнение:
| [11] | ||
| Контролируемая фаза S | 2 |  |
| [6] |
Фазовый сдвиг — это семейство однокубитных вентилей, которые отображают базовые состояния. и . Вероятность измерения или не изменяется после применения этого вентиля, однако он изменяет фазу квантового состояния. Это эквивалентно отслеживанию горизонтального круга (линии широты) или вращению вдоль оси z на сфере Блоха с помощью радианы. Типичным примером являются Т- ворота, где (исторически известный как вентиль), фазовый вентиль. Обратите внимание, что некоторые вентили Клиффорда являются частными случаями вентиля фазового сдвига:
Аргумент для вентиля фазового сдвига находится в U(1) , и вентиль выполняет поворот фазы в U(1) вдоль заданного базисного состояния (например, вращает фазу вокруг ) . Расширение вращение вокруг общей фазы обоих базисных состояний двухуровневой квантовой системы ( кубита ) может быть выполнено с помощью последовательной схемы : . Когда эти ворота являются оператором вращения ворота и если это глобальный этап. [а] [б]
Т - ворот Историческое название Ворота исходят из личности , где .
Произвольные однокубитные фазовые вентили изначально доступны для трансмонных квантовых процессоров за счет синхронизации микроволновых управляющих импульсов. [13] Это можно объяснить сменой кадра . [14] [15]
Как и в случае с любым одним кубитным вентилем, можно построить управляемую версию вентиля с фазовым сдвигом. Что касается вычислительной основы, 2-кубитный управляемый вентиль фазового сдвига: сдвигает фазу с только если оно действует на государство :
Вентиль с контролируемым Z (или CZ) — это особый случай, когда .
Ворота с контролируемым S — это случай контролируемого когда и это часто используемые ворота. [6]
Ворота оператора ротации
[ редактировать ]| Имена | # кубитов | Символ оператора | Экспоненциальная форма | Матрица | Принципиальная схема | Характеристики | Ссылки |
|---|---|---|---|---|---|---|---|
| Вращение вокруг X оси | 1 |
| [1] [6] | ||||
| Вращение вокруг оси Y | 1 |
| [1] [6] | ||||
| Вращение вокруг оси Z | 1 |
| [1] [6] |
Ворота оператора вращения и являются аналоговыми матрицами вращения в трех декартовых осях SO (3) [с] , вдоль осей x, y или z проекции сферы Блоха .
Поскольку матрицы Паули связаны с генератором вращений, эти операторы вращения можно записать в виде матричной экспоненты с матрицами Паули в аргументе. Любой унитарная матрица в SU(2) может быть записана как произведение (т.е. последовательная схема) трех или менее вентилей вращения. Обратите внимание, что для двухуровневых систем, таких как кубиты и спиноры , эти вращения имеют период 4π . Поворот на 2π (360 градусов) возвращает тот же вектор состояния с другой фазой . [16]
У нас также есть и для всех
Матрицы вращения связаны с матрицами Паули следующим образом:
Можно вычислить сопряженное действие вращений на вектор Паули , а именно эффективное вращение на двойной угол a, чтобы применить формулу вращения Родригеса :
Скалярное произведение любого единичного вектора с приведенной выше формулой генерирует выражение любого одиночного кубитного вентиля, помещенного в смежные вентили вращения. Например, можно показать, что . Кроме того, используя антикоммутационное соотношение, мы имеем .
Операторы вращения имеют интересную идентичность. Например, и Кроме того, используя антикоммутационные отношения, мы имеем и
Глобальную фазу и фазовый сдвиг можно преобразовать друг в друга с помощью оператора Z-вращения: . [5] : 11 [1] : 77–83
The Ворота представляют собой вращение на π/2 вокруг оси x в сфере Блоха. .
Аналогичные вентили оператора вращения существуют для SU(3) с использованием матриц Гелл-Манна . Это операторы вращения, используемые с кутритами .
Двухкубитные ворота взаимодействия
[ редактировать ]| Имена | # кубитов | Символ оператора | Экспоненциальная форма | Матрица | Принципиальная схема | Характеристики | Ссылки |
|---|---|---|---|---|---|---|---|
| ХХ взаимодействие | 2 | , |
Выполнение: | [ нужна ссылка ] | |||
| ГГ взаимодействие | 2 | , |
Выполнение: | [ нужна ссылка ] | |||
| ZZ-взаимодействие | 2 | , |
| [ нужна ссылка ] | |||
| XY, ХХ плюс ГГ | 2 | , |
| [ нужна ссылка ] |
Взаимодействие кубит-кубит Изинга или ворота взаимодействия Гейзенберга R xx , R yy и R zz представляют собой 2-кубитные ворота, которые изначально реализованы в некоторых квантовых компьютерах с захваченными ионами , используя, например, процедуру ворот Мёльмера-Сёренсена . [17] [18]
Обратите внимание, что эти элементы также могут быть выражены в синусоидальной форме, например .
Вентиль CNOT можно дополнительно разложить на продукты вентилей оператора вращения и ровно один двухкубитный вентиль взаимодействия, например
Вентиль SWAP может быть построен из других вентилей, например, с использованием двухкубитных вентилей взаимодействия : .
В сверхпроводящих схемах семейство вентилей, возникающее в результате взаимодействий Гейзенберга, иногда называют набором вентилей fSim . Их можно реализовать с использованием настраиваемых по потоку кубитов с настраиваемой по потоку связью. [19] или использование СВЧ-приводов в кубитах с фиксированной частотой и фиксированной связью. [20]
Подкачивающие ворота без Клиффорда
[ редактировать ]| Имена | # кубитов | Символ оператора | Матрица | Принципиальная схема | Характеристики | Ссылки |
|---|---|---|---|---|---|---|
| Замена квадратного корня | 2 |  | [1] | |||
| Мнимый обмен квадратным корнем | 2 |
| [11] | |||
| Обмен (возведенный в степень) | 2 | 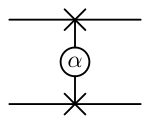 |
| [1] | ||
| Фред тоже , контролируемый своп | 3 | , |  или  |
| [1] [6] |
Вентиль √ SWAP выполняет половину обмена двух кубитов (см. вентили Клиффорда). Он универсален, так что любой многокубитный вентиль может быть построен только из √ SWAP и однокубитных вентилей. более одного применения √ SWAP из состояний продукта требуется Для создания состояния Белла . Ворота √ SWAP естественным образом возникают в системах, использующих обменное взаимодействие . [21] [1]
Для систем с изинговскими взаимодействиями иногда более естественно ввести воображаемый обмен [22] или iSWAP. [23] [24] Обратите внимание, что и или в более общем плане для всех действительных n, кроме 0.
МЕНЯТЬ а естественным образом возникает в спинтронных квантовых компьютерах. [1]
Гейт Фредкина (также CSWAP или CS-гейт), названный в честь Эдварда Фредкина , представляет собой 3-битный вентиль, выполняющий контролируемую замену . Он универсален для классических вычислений. У него есть то полезное свойство, что количество нулей и единиц сохраняется повсюду, что в модели бильярдного шара означает, что на выходе выводится одинаковое количество шаров, а на входе.
Другие названные ворота
[ редактировать ]| Имена | # кубитов | Символ оператора | Матрица | Принципиальная схема | Характеристики | Назван в честь | Ссылки |
|---|---|---|---|---|---|---|---|
| Общее вращение одного кубита | 1 |
| OpenQASM U-воротник [д] | [11] [25] | |||
| Баренц | 2 |
| Адриано Баренц | [1] | |||
| Беркли Б | 2 |
| Калифорнийский университет в Беркли [26] | [1] | |||
| Контролируемый-V, контролируемый квадратный корень НЕ | 2 | [9] | |||||
| Запутывание ядра, каноническое разложение | 2 | , |
| [1] | |||
| Дагвуд Бамстед | 2 |
| Комикс Дагвуд Бамстед [27] | [28] [27] | |||
| Эхо-перекрестный резонанс | 2 |
| [29] | ||||
| Фермионное моделирование | 2 | , |
| [30] [19] [31] | |||
| Гивенс | 2 | , |
| Ротации Гивенса | [32] | ||
| Магия | 2 | [1] | |||||
| Платан | 2 | , | Google Sycamore Процессор | [33] | |||
| CZ-ОБМЕН | 2 | , |
| [34] | |||
| немецкий | 3 | , |
| Дэвид Дойч | [1] | ||
| Марголюс, упрощенный Тоффоли | 3 | , |  |
| Норман Марголус | [35] [36] | |
| Перес | 3 | , |  |
| Ашер Перес | [37] | |
| Тоффоли , контролируемый-контролируемый НЕ | 3 |  |
| Томмазо Тоффоли | [1] [6] | ||
Фермион-Фредкин, Управляемо-фермионный SWAP | 3 | , , | [34] |
Примечания
[ редактировать ]- ^ когда , где является сопряженным транспонированием (или эрмитовым сопряженным ).
- ^ Также:
- ^ SU (2) двойная обложка . См. также расслоение Хопфа .
- ^ Показанная здесь матрица взята из openQASM 3.0, которая отличается от из глобальной фазы (вентиль OpenQASM 2.0 U находится в SU(2)).
Ссылки
[ редактировать ]- ^ Перейти обратно: а б с д и ж г час я дж к л м н тот п д р с т в v В х и С аа аб и объявление но Уильямс, Колин П. (2011). Исследования в области квантовых вычислений . Спрингер . ISBN 978-1-84628-887-6 .
- ^ "ИГейт" . qiskit.org . Онлайн-документация Qiskit .
- ^ «Я операция» . docs.microsoft.com . 28 июля 2023 г. Q# . Онлайн-документация
- ^ Фейнман, Ричард П. (1986). «Квантово-механические компьютеры». Основы физики . 16 (6). Springer Science and Business Media LLC: 507–531. Бибкод : 1986FoPh...16..507F . дои : 10.1007/bf01886518 . ISSN 0015-9018 . S2CID 122076550 .
- ^ Перейти обратно: а б Баренко, Адриано; Беннетт, Чарльз Х.; Клив, Ричард; ДиВинченцо, Дэвид П.; Марголус, Норман; Шор, Питер; Слитор, Тихо; Смолин, Джон А.; Вайнфуртер, Харальд (1 ноября 1995 г.). «Элементарные вентили для квантовых вычислений». Физический обзор А. 52 (5). Американское физическое общество (APS): 3457–3467. arXiv : Quant-ph/9503016 . Бибкод : 1995PhRvA..52.3457B . дои : 10.1103/physreva.52.3457 . ISSN 1050-2947 . ПМИД 9912645 . S2CID 8764584 .
- ^ Перейти обратно: а б с д и ж г час я дж к л м н тот п Нильсен, Майкл А. (2010). Квантовые вычисления и квантовая информация . Исаак Л. Чуанг (изд. к 10-летию). Кембридж: Издательство Кембриджского университета. ISBN 978-1-107-00217-3 . OCLC 665137861 .
- ^ Хунг, WNN; Сяоюй Сун; Гуоу Ян; Цзинь Ян; Перковский, М. (сентябрь 2006 г.). «Оптимальный синтез нескольких выходных булевых функций с использованием набора квантовых вентилей путем символического анализа достижимости». Транзакции IEEE по автоматизированному проектированию интегральных схем и систем . 25 (9): 1652–1663. дои : 10.1109/tcad.2005.858352 . ISSN 0278-0070 . S2CID 14123321 .
- ^ Коллинз, Дэниел; Линден, Ной; Попеску, Санду (7 августа 2001 г.). «Нелокальное содержание квантовых операций» . Физический обзор А. 64 (3): 032302. arXiv : quant-ph/0005102 . Бибкод : 2001PhRvA..64c2302C . дои : 10.1103/PhysRevA.64.032302 . ISSN 1050-2947 . S2CID 29769034 .
- ^ Перейти обратно: а б Патхак, Анирбан (20 июня 2013 г.). Элементы квантовых вычислений и квантовой связи . Тейлор и Фрэнсис. ISBN 978-1-4665-1792-9 .
- ^ Янофски, Носон С.; Маннуччи, Мирко А. (11 августа 2008 г.). Квантовые вычисления для ученых-компьютерщиков . Издательство Кембриджского университета. ISBN 978-1-139-64390-0 .
- ^ Перейти обратно: а б с д Стэнсил, Дэниел Д.; Берд, Грегори Т. (19 апреля 2022 г.). Принципы сверхпроводящих квантовых компьютеров . Джон Уайли и сыновья. ISBN 978-1-119-75074-1 .
- ^ Д. Якш, Дж. И. Сирак, П. Золлер, С. Л. Ролстон, Р. Коте и М. Д. Лукин (2000). «Быстрые квантовые ворота для нейтральных атомов» . Физ. Преподобный Летт . 85 (10): 2208. arXiv : quant-ph/0004038 . doi : 10.1103/PhysRevLett.85.2208 .
{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Дибьенду Чаттерджи, Ариджит Рой (2015). «Схема квантового полусумматора на основе трансмонов» . Успехи теоретической и экспериментальной физики . 2015 (9): 7–8. Бибкод : 2015PTEP.2015i3A02C . дои : 10.1093/ptep/ptv122 .
- ^ Маккей, Дэвид С.; Вуд, Кристофер Дж.; Шелдон, Сара; Чоу, Джерри М.; Гамбетта, Джей М. (31 августа 2017 г.). «Эффективные Z-вентили для квантовых вычислений». Физический обзор А. 96 (2): 022330. arXiv : 1612.00858 . Бибкод : 2015PTEP.2015i3A02C . дои : 10.1093/ptep/ptv122 .
- ^ "qiskit.circuit.library.PhaseGate" . IBM (документация qiskit).
- ^ Гриффитс, диджей (2008). Введение в элементарные частицы (2-е изд.). Джон Уайли и сыновья . стр. 127–128. ISBN 978-3-527-40601-2 .
- ^ «Конференция в Монро» (PDF) . online.kitp.ucsb.edu .
- ^ «Демонстрация небольшого программируемого квантового компьютера с атомными кубитами» (PDF) . Проверено 10 февраля 2019 г.
- ^ Перейти обратно: а б Фоксен, Б.; Нил, Дж.; Дансворт, А.; Рушан, П.; Кьяро, Б.; Мегрант, А.; Келли, Дж.; Чен, Цзыцзюнь; Сатцингер, К.; Барендс, Р.; Аруте, Ф.; Арья, К.; Бэббуш, Р.; Бэкон, Д.; Бардин, Джей Джей; Бойшо, С.; Бьюэлл, Д.; Беркетт, Б.; Чен, Ю; Коллинз, Р.; Фархи, Э.; Фаулер, А.; Гидни, Дж.; Юстина, М.; Графф, Р.; Харриган, М.; Хуанг, Т.; Исаков С.В.; Джеффри, Э.; Цзян, З.; Кафри, Д.; Кечеджи, К.; Климов П.; Коротков А.; Кострица, Ф.; Ландхейс, Д.; Лусеро, Э.; МакКлин, Дж.; МакИвен, М.; Ми, Х.; Мохсени, М.; Мутус, JY; Нааман, О.; Нили, М.; Ню, М.; Петухов А.; Кинтана, К.; Рубин, Н.; Санк, Д.; Смелянский В.; Вайнзенчер, А.; Уайт, ТК; Яо, З.; Ага, П.; Зальцман, А.; Невен, Х.; Мартинис, Дж. М. (15 сентября 2020 г.). «Демонстрация непрерывного набора двухкубитных вентилей для краткосрочных квантовых алгоритмов». Письма о физических отзывах . 125 (12). arXiv : 2001.08343 . doi : 10.1103/PhysRevLett.125.120504 . ISSN 0031-9007 .
- ^ Нгуен, Л.Б.; Ким, Ю.; Хашим, А.; Госс, Н.; Маринелли, Б.; Бхандари, Б.; Дас, Д.; Наик, РК; Крейкебаум, Дж. М.; Джордан, А.; Сантьяго, ДИ; Сиддики, И. (16 января 2024 г.). «Программируемые гейзенберговские взаимодействия между кубитами Флоке» . Физика природы . 20 (1): 240–246. arXiv : 2211.10383 . Бибкод : 2024NatPh..20..240N . дои : 10.1038/s41567-023-02326-7 .
- ^ Немировский, Джонатан; Саги, Йоав (2021), «Быстрый универсальный двухкубитный вентиль для нейтральных фермионных атомов в оптических пинцетах», Physical Review Research , 3 (1): 013113, arXiv : 2008.09819 , Bibcode : 2021PhRvR...3a3113N , doi : 10.1103/ PhysRevResearch.3.013113
- ^ Расмуссен, SE; Зиннер, Северная Каролина (17 июля 2020 г.). «Простая реализация высокоточных вентилей с контролируемой заменой и возведение в степень квантовой схемы неэрмитовых вентилей» . Обзор физических исследований . 2 (3): 033097. arXiv : 2002.11728 . Бибкод : 2020PhRvR...2c3097R . doi : 10.1103/PhysRevResearch.2.033097 . ISSN 2643-1564 .
- ^ Шух, Норберт; Зиверт, Йенс (10 марта 2003 г.). «Естественный двухкубитный вентиль для квантовых вычислений с использованием взаимодействия XY» . Физический обзор А. 67 (3): 032301. arXiv : quant-ph/0209035 . Бибкод : 2003PhRvA..67c2301S . дои : 10.1103/PhysRevA.67.032301 . ISSN 1050-2947 . S2CID 50823541 .
- ^ Даллер-Демерс, Пьер-Люк; Вильгельм, Франк К. (05 декабря 2016 г.). «Квантовые ворота и архитектура для квантового моделирования модели Ферми-Хаббарда» . Физический обзор А. 94 (6): 062304. arXiv : 1606.00208 . Бибкод : 2016PhRvA..94f2304D . дои : 10.1103/PhysRevA.94.062304 . ISSN 2469-9926 . S2CID 118408193 .
- ^ Кросс, Эндрю; Джавади-Абхари, Али; Александр, Томас; Де Бодрап, Ниль; епископ Лев С.; Хидель, Стивен; Райан, Колм А.; Шивараджа, Прасант; Смолин, Джон; Гамбетта, Джей М.; Джонсон, Блейк Р. (2022). «OpenQASM 3: более широкий и глубокий квантовый ассемблер» . Транзакции ACM в квантовых вычислениях . 3 (3): 1–50. arXiv : 2104.14722 . дои : 10.1145/3505636 . ISSN 2643-6809 . S2CID 233476587 .
- ^ Чжан, Цзюнь; Вала, Иржи; Шастри, Шанкар; Уэйли, К. Биргитта (7 июля 2004 г.). «Минимальная конструкция двухкубитных квантовых операций» . Письма о физических отзывах . 93 (2): 020502. arXiv : quant-ph/0312193 . Бибкод : 2004PhRvL..93b0502Z . doi : 10.1103/PhysRevLett.93.020502 . ISSN 0031-9007 . ПМИД 15323888 . S2CID 9632700 .
- ^ Перейти обратно: а б АбуГанем, М. (01 января 2021 г.). «Двухкубитные ворота запутанности для сверхпроводящих квантовых компьютеров» . Рочестер, Нью-Йорк. дои : 10.2139/ssrn.4188257 . S2CID 252264545 . ССНН 4188257 .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) - ^ Петерсон, Эрик С.; Крукс, Гэвин Э.; Смит, Роберт С. (26 марта 2020 г.). «Двухкубитные схемы фиксированной глубины и многогранник монодромии» . Квантовый . 4 : 247. arXiv : 1904.10541 . doi : 10.22331/кв-2020-03-26-247 . S2CID 214690323 .
- ^ Корколес, AD; Магесан, Иасвар; Шринивасан, Шрикант Дж.; Кросс, Эндрю В.; Штеффен, М.; Гамбетта, Джей М.; Чоу, Джерри М. (29 апреля 2015 г.). «Демонстрация квантового кода обнаружения ошибок с использованием квадратной решетки из четырех сверхпроводящих кубитов» . Природные коммуникации . 6 (1): 6979. arXiv : 1410,6419 . Бибкод : 2015NatCo...6.6979C . дои : 10.1038/ncomms7979 . ISSN 2041-1723 . ПМЦ 4421819 . ПМИД 25923200 .
- ^ Кириенко, Александр; Эльфвинг, Винсент Э. (15 ноября 2021 г.). «Обобщенные правила дифференцирования квантовых цепей» . Физический обзор А. 104 (5): 052417. arXiv : 2108.01218 . Бибкод : 2021PhRvA.104e2417K . дои : 10.1103/PhysRevA.104.052417 . hdl : 10871/127818 . ISSN 2469-9926 . S2CID 236881494 .
- ^ Нгуен, Л.Б.; Ким, Ю.; Хашим, А.; Госс, Н.; Маринелли, Б.; Бхандари, Б.; Дас, Д.; Наик, РК; Крейкебаум, Дж. М.; Джордан, А.; Сантьяго, ДИ; Сиддики, И. (16 января 2024 г.). «Программируемые гейзенберговские взаимодействия между кубитами Флоке» . Физика природы . 20 (1): 240–246. arXiv : 2211.10383 . Бибкод : 2024NatPh..20..240N . дои : 10.1038/s41567-023-02326-7 .
- ^ Арразола, Джон Майкл; Мэтью, Оливия; Кесада, Николас; Джахангири, Соран; Тонкий, Ален; Киллоран, Натан (20 июня 2022 г.). «Универсальные квантовые схемы для квантовой химии» . Квантовый . 6 : 742.arXiv : 2106.13839 . Бибкод : 2022Quant...6..742A . doi : 10.22331/q-2022-06-20-742 . S2CID 235658488 .
- ^ Аруте, Фрэнк; Арья, Кунал; Бэббуш, Райан; Бэкон, Дэйв; Бардин, Джозеф К.; Барендс, Рами; Бисвас, Рупак; Бойшо, Серхио; Брандао, Фернандо ГСЛ; Бьюэлл, Дэвид А.; Беркетт, Брайан; Чен, Ю; Чен, Цзыцзюнь; Кьяро, Бен; Коллинз, Роберто (2019). «Квантовое превосходство с помощью программируемого сверхпроводникового процессора» . Природа . 574 (7779): 505–510. arXiv : 1910.11333 . Бибкод : 2019Natur.574..505A . дои : 10.1038/s41586-019-1666-5 . ISSN 1476-4687 . PMID 31645734 . S2CID 204836822 .
- ^ Перейти обратно: а б Гу, Сю; Фернандес-Пендас, Хорхе; Викстол, Понт; Абад, Тахере; Уоррен, Кристофер; Бенгтссон, Андреас; Танкреди, Джованна; Шумейко, Виталий; Байландер, Джонас; Йоханссон, Йоран; Фриск Кокум, Антон (2021). «Быстрые многокубитные вентили посредством одновременных двухкубитных вентилей» . PRX Квантум . 2 (4): 040348. arXiv : 2108.11358 . дои : 10.1103/PRXQuantum.2.040348 . ISSN 2691-3399 .
- ^ Маслов, Дмитрий (10 февраля 2016 г.). «Преимущества использования вентилей Тоффоли относительной фазы с применением для оптимизации Тоффоли с множественным управлением» . Физический обзор А. 93 (2): 022311. arXiv : 1508.03273 . Бибкод : 2016PhRvA..93b2311M . doi : 10.1103/PhysRevA.93.022311 . ISSN 2469-9926 . S2CID 5226873 .
- ^ Сун, Гуан; Клаппенекер, Андреас (31 декабря 2003 г.). «Упрощенная реализация ворот Тоффоли от Margolus является оптимальной». arXiv : Quant-ph/0312225 . Бибкод : 2003quant.ph.12225S .
{{cite journal}}: Для цитирования журнала требуется|journal=( помощь ) - ^ Таплиял, Химаншу; Ранганатан, Нагараджан (2009). «Разработка эффективных обратимых двоичных вычитателей на основе нового обратимого вентиля» . Ежегодный симпозиум IEEE Computer Society 2009 г. по СБИС . стр. 229–234. дои : 10.1109/ISVLSI.2009.49 . ISBN 978-1-4244-4408-3 . S2CID 16182781 .
- ^ Уоррен, Кристофер; Фернандес-Пендас, Хорхе; Ахмед, Шахнаваз; Абад, Тахере; Бенгтссон, Андреас; Бизнарова, Янка; Дебнатх, Каманасиш; Гу, Сю; Крижан, Кристиан; Осман, Амр; Фадави Рудсари, Анита; Дельсинг, Пер; Йоханссон, Йоран; Фриск Кокум, Антон; Танкреди, Джованна; Байландер, Джонас (2023). «Расширенная характеристика и реализация семейства трехкубитных вентилей на пределе когерентности» . npj Квантовая информация . 9 (1): 44. arXiv : 2207.02938 . дои : 10.1038/s41534-023-00711-x . ISSN 2056-6387 .



































![{\textstyle {\text{контролируется[0]-НЕ}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/666bd05c87c61de2047eb0613ea0730f86667f31)


















![{\textstyle {\sqrt[{4}]{Z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b2ff605c151630e78170afaaae7365137570604)

































































![{\displaystyle {\displaystyle \exp \left[-i {\frac {\phi }{4}}(X\otimes X+Y\otimes Y)\right]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46dd699acee993bb1dfdcaae40b6dfa6c8462db5)

















![{\displaystyle {\sqrt[{n}]{i{\mbox{SWAP}}}}=R_ {xx}(-\pi /2n)R_{yy}(-\pi /2n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f10366d0d56f5eff91c562190970f5c654c15992)








![{\displaystyle \exp \left[i {\frac {\pi }{8}}(2X\otimes X+Y\otimes Y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79e291eb824b8455eb9a3f59bf9084f5aaa24535)






![{\displaystyle \exp \left [i (aX\otimes X+bY\otimes Y+cZ\otimes Z)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10fddc558772c4ace4b390095ac1c5cecddf273)



![{\displaystyle \exp \left[-i {\frac {3\pi }{16}}(X\otimes X+Y\otimes Y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bdec91d774e918820d8b3a2abbe9ce13939a7cf)









![{\displaystyle \exp \left[-i {\frac {\theta }{2}}(Y\otimes XX\otimes Y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e807329af5f546f7c2f758c153dce7f0d4c79e93)

























