Седловая точка

В математике — седловая точка или минимаксная точка. ^[1] — это точка на поверхности графика функции , в которой все наклоны (производные) в ортогональных направлениях равны нулю ( критическая точка ), но которая не является локальным экстремумом функции. ^[2] Примером седловой точки является критическая точка с относительным минимумом в одном осевом направлении (между пиками) и относительным максимумом вдоль оси пересечения. Однако седловая точка не обязательно должна иметь такую форму. Например, функция $f(x,y)=x^{2}+y^{3}$ имеет критическую точку $(0,0)$ это седловая точка, поскольку она не является ни относительным максимумом, ни относительным минимумом, но не имеет относительного максимума или относительного минимума в $y$ -направление.

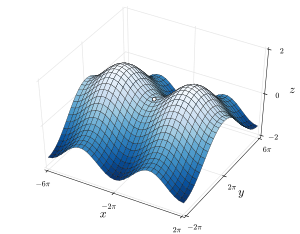
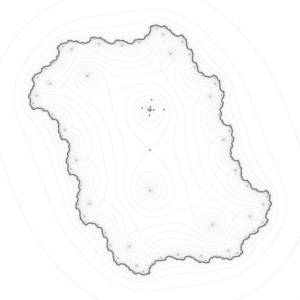
Название происходит от того факта, что прототипный пример в двух измерениях представляет собой поверхность , которая изгибается вверх в одном направлении и изгибается вниз в другом направлении, напоминая седло для верховой езды . С точки зрения контурных линий , седловая точка в двух измерениях порождает контурную карту с парой линий, пересекающихся в этой точке. Такие пересечения редки на реальных картах обзора боеприпасов, поскольку высота седловой точки вряд ли будет совпадать с целочисленными кратными, используемыми на таких картах. Вместо этого седловая точка выглядит как пустое пространство посередине четырех наборов контурных линий, которые приближаются и отклоняются от нее. Для базовой седловой точки эти наборы встречаются парами, причем противостоящая пара высокого уровня и противостоящая пара низкого уровня расположены в ортогональных направлениях. Критические контурные линии обычно не обязательно должны пересекаться ортогонально.

Математическая дискуссия

Простой критерий проверки того, является ли данная стационарная точка действительной функции F ( x , y функции ) двух действительных переменных седловой точкой, состоит в вычислении матрицы Гессе в этой точке: если гессиан неопределенен , то эта точка является седловой точкой. Например, матрица Гессе функции $z=x^{2}-y^{2}$ в стационарной точке $(x,y,z)=(0,0,0)$ это матрица

{\begin{bmatrix}2&0\\0&-2\\\end{bmatrix}}

что является неопределенным. Следовательно, эта точка является седловой. Этот критерий дает лишь достаточное условие. Например, точка $(0,0,0)$ является седловой точкой функции $z=x^{4}-y^{4},$ но матрица Гессе этой функции в начале координат является нулевой матрицей , которая не является неопределенной.

В самых общих чертах седловая точка ( гладкой функции график которой представляет собой кривую , поверхность или гиперповерхность ) — это стационарная точка, такая что кривая/поверхность/и т. д. в окрестности этой точки не находится полностью ни на одной из сторон касательного пространства в этой точке.

В одномерной области седловая точка — это точка , которая является одновременно точкой покоя и точкой перегиба . Поскольку это точка перегиба, она не является локальным экстремумом .

Седловидная поверхность

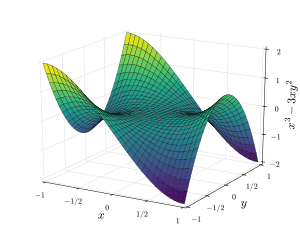
Седловая поверхность — это гладкая поверхность, содержащая одну или несколько седловых точек.

Классическими примерами двумерных седловых поверхностей в евклидовом пространстве являются поверхности второго порядка, гиперболический параболоид. $z=x^{2}-y^{2}$ (которую часто называют « седловой поверхностью» или «стандартной седловой поверхностью») и однолистным гиперболоидом . Картофельные чипсы или чипсы Pringles — это повседневный пример гиперболической параболоидной формы.

Седловые поверхности имеют отрицательную гауссову кривизну , что отличает их от выпуклых/эллиптических поверхностей, имеющих положительную гауссову кривизну. Классической поверхностью седла третьего порядка является седло обезьяны . ^[3]

Примеры

для двух игроков, В игре с нулевой суммой определенной в непрерывном пространстве, точка равновесия является седловой точкой.

Для линейной автономной системы второго порядка критическая точка является седловой, если характеристическое уравнение имеет одно положительное и одно отрицательное действительное собственное значение . ^[4]

При оптимизации с учетом ограничений равенства условия первого порядка описывают седловую точку лагранжиана .

Другое использование

В динамических системах , если динамика задается дифференцируемым отображением f , то точка является гиперболической тогда и только тогда, когда дифференциал ƒ ^н (где n - период точки) не имеет собственного значения на (комплексном) единичном круге при вычислении в точке. Затемседловая точка — это гиперболическая периодическая точка которой , устойчивое и неустойчивое многообразия имеют размерность , отличную от нуля.

Седловая точка матрицы — это элемент, который является одновременно наибольшим элементом в своем столбце и наименьшим элементом в своей строке.

См. также

Метод перевала является расширением метода Лапласа аппроксимации интегралов.
Максимум и минимум
Производный тест
Гиперболическая точка равновесия
Гиперболическая геометрия
Теорема о минимаксе
Неравенство Макс-Мин
Седло обезьяны
Теорема о горном перевале

Ссылки

Цитаты

^ Ховард Антон, Ирл Бивенс, Стивен Дэвис (2002): Исчисление, многовариантная версия , стр. 844.
^ Чан, Альфа К. (1984). Фундаментальные методы математической экономики (3-е изд.). Нью-Йорк: МакГроу-Хилл . п. 312 . ISBN 0-07-010813-7 .
^ Бак, Р. Крейтон (2003). Продвинутое исчисление (3-е изд.). Лонг-Гроув, Иллинойс: Waveland Press . п. 160. ИСБН 1-57766-302-0 .
^ фон Петерсдорф 2006

Источники

Грей, Лоуренс Ф.; Фланиган, Фрэнсис Дж.; Каздан, Джерри Л.; Фрэнк, Дэвид Х.; Фристедт, Берт (1990), Второе исчисление: линейные и нелинейные функции , Берлин: Springer-Verlag, с. 375 , ISBN 0-387-97388-5
Гильберт, Дэвид ; Кон-Воссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк, Нью-Йорк: Челси , ISBN 978-0-8284-1087-8
фон Петерсдорф, Тобиас (2006), «Критические точки автономных систем» , Дифференциальные уравнения для ученых и инженеров (конспекты лекций по математике 246)
Виддер, Д.В. (1989), Продвинутое исчисление , Нью-Йорк, Нью-Йорк: Dover Publications, стр. 128, ISBN 0-486-66103-2
Агарвал А. Исследование равновесия Нэша (конспект лекций)

Дальнейшее чтение

Гильберт, Дэвид ; Кон-Воссен, Стефан (1952). Геометрия и воображение (2-е изд.). Челси. ISBN 0-8284-1087-9 .

Внешние ссылки

СМИ, связанные с седловой точкой, на Викискладе?

[1] Ховард Антон, Ирл Бивенс, Стивен Дэвис (2002): Исчисление, многовариантная версия , стр. 844.

[2] Чан, Альфа К. (1984). Фундаментальные методы математической экономики (3-е изд.). Нью-Йорк: МакГроу-Хилл . п. 312 . ISBN 0-07-010813-7 .

[3] Бак, Р. Крейтон (2003). Продвинутое исчисление (3-е изд.). Лонг-Гроув, Иллинойс: Waveland Press . п. 160. ИСБН 1-57766-302-0 .

[4] фон Петерсдорф 2006

[1]

[2]

[3]

[4]