Семиугольная сотовая плитка
| Семиугольная сотовая плитка | |
|---|---|
| Тип | Обычные соты |
| Символ Шлефли | {7,3,3} |
| Диаграмма Кокстера | |
| Клетки | {7,3}  |
| Лица | Семиугольник {7} |
| Вершинная фигура | тетраэдр {3,3} |
| Двойной | {3,3,7} |
| Группа Коксетера | [7,3,3] |
| Характеристики | Обычный |
В геометрии гиперболического трехмерного пространства семиугольная мозаика в виде сот или сот 7,3,3 представляет собой обычную мозаику , заполняющую пространство (или соты ). Каждая бесконечная ячейка состоит из семиугольной мозаики , вершины которой лежат на 2-гиперцикле , каждый из которых имеет предельную окружность на идеальной сфере.
Геометрия
[ редактировать ]Символ Шлефли для сот из семиугольных плиток - {7,3,3}, с тремя семиугольными плитками, сходящимися на каждом краю. Вершинной фигурой этой соты является тетраэдр {3,3}.
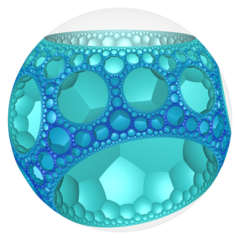 Модель диска Пуанкаре (по центру вершины) | 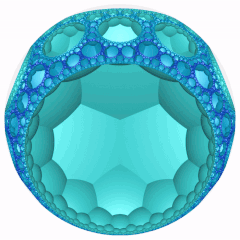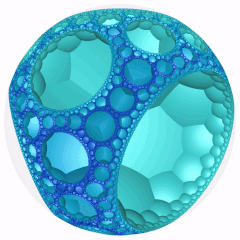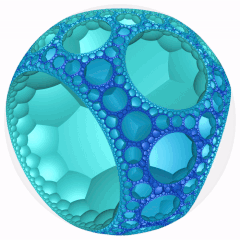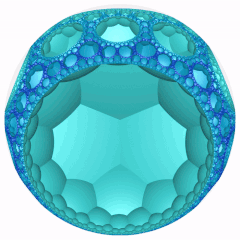 Вращающийся |  Идеальная поверхность |
Связанные многогранники и соты
[ редактировать ]Это часть серии правильных многогранников и сот с символом { p ,3,3} Шлефли и тетраэдральными вершинными фигурами :
| {p,3,3} соты |
|---|
Это часть серии правильных сот {7,3, p }.
| {7,3,3} | {7,3,4} | {7,3,5} | {7,3,6} | {7,3,7} | {7,3,8} | ... {7,3,∞} |
|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |
Это часть серии обычных сот с {7, p , 3}.
| {7,3,3} | {7,4,3} | {7,5,3} ... |
|---|---|---|
 |  |  |
Восьмиугольная сотовая плитка
[ редактировать ]| Восьмиугольная сотовая плитка | |
|---|---|
| Тип | Обычные соты |
| Символ Шлефли | {8,3,3} т{8,4,3} 2т{4,8,4} т{4 [3,3] } |
| Диаграмма Кокстера | |
| Клетки | {8,3}  |
| Лица | Восьмиугольник {8} |
| Вершинная фигура | тетраэдр {3,3} |
| Двойной | {3,3,8} |
| Группа Коксетера | [8,3,3] |
| Характеристики | Обычный |
В геометрии гиперболического трехмерного пространства восьмиугольная мозаика в виде сот или сот 8,3,3 представляет собой обычную мозаику , заполняющую пространство (или соты ). Каждая бесконечная ячейка состоит из восьмиугольной мозаики , вершины которой лежат на 2-гиперцикле , каждый из которых имеет предельную окружность на идеальной сфере.
Символ Шлефли для восьмиугольных сот — {8,3,3}, с тремя восьмиугольными плитками, сходящимися на каждом краю. Вершинной фигурой этой соты является тетраэдр {3,3}.
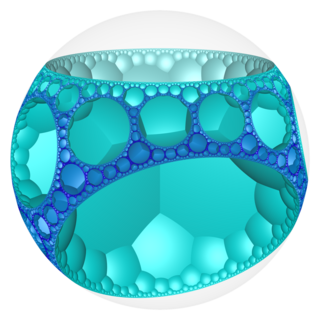 Модель диска Пуанкаре (центрированная по вершинам) | 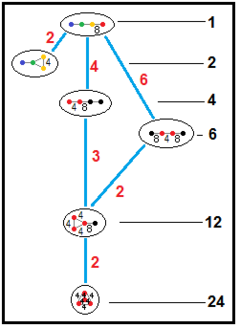 Прямые подгруппы из [8,3,3] |
Апейрогональная плитка в виде сот
[ редактировать ]| Апейрогональная плитка в виде сот | |
|---|---|
| Тип | Обычные соты |
| Символ Шлефли | {∞,3,3} т{∞,3,3} 2t{∞,∞,∞} т{∞ [3,3] } |
| Диаграмма Кокстера | |
| Клетки | {∞,3}  |
| Лица | Апейрогон {∞} |
| Вершинная фигура | тетраэдр {3,3} |
| Двойной | {3,3,∞} |
| Группа Коксетера | [∞,3,3] |
| Характеристики | Обычный |
В геометрии гиперболического трехмерного пространства апейрогональная мозаика-сота или ∞,3,3-сота представляет собой регулярную мозаику , заполняющую пространство (или соты ). Каждая бесконечная ячейка состоит из апейрогонального мозаики , вершины которой лежат на 2-гиперцикле , каждый из которых имеет предельную окружность на идеальной сфере.
Символ Шлефли для сот апейрогональной мозаики — {∞,3,3}, с тремя апейрогональными мозаиками, сходящимися на каждом краю. Вершинной фигурой этой соты является тетраэдр {3,3}.
Проекция «идеальной поверхности» ниже представляет собой плоскость на бесконечности в модели полупространства Пуанкаре H3. На нем изображен аполлонический узор из кругов внутри самого большого круга.
 Модель диска Пуанкаре (центрированная по вершинам) | 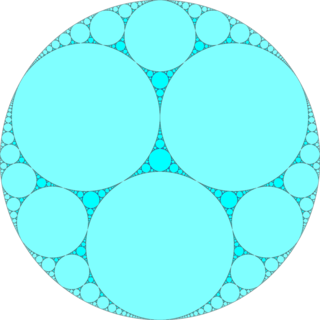 Идеальная поверхность |
См. также
[ редактировать ]Ссылки
[ редактировать ]- Коксетер , Правильные многогранники , 3-е. изд., Dover Publications, 1973. ISBN 0-486-61480-8 . (Таблицы I и II: Правильные многогранники и соты, стр. 294–296)
- Красота геометрии: двенадцать эссе (1999), Dover Publications, LCCN 99-35678 , ISBN 0-486-40919-8 (Глава 10, Обычные соты в гиперболическом пространстве , архивировано 10 июня 2016 г. в Wayback Machine ) Таблица III
- Джеффри Р. Уикс. Форма пространства, 2-е издание ISBN 0-8247-0709-5 (главы 16–17: Геометрии трехмерных многообразий I, II)
- Джордж Максвелл, Сферические упаковки и группы гиперболического отражения , ЖУРНАЛ АЛГЕБРЫ 79,78-97 (1982) [1]
- Хао Чен, Жан-Филипп Лаббе, лоренцианские группы Кокстера и шаровые упаковки Бойда-Максвелла , (2013) [2]
- Визуализация гиперболических сот arXiv:1511.02851 Ройс Нельсон, Генри Сегерман (2015)
Внешние ссылки
[ редактировать ]- Джон Баез , Визуальные идеи : {7,3,3} Honeycomb (01.08.2014) {7,3,3} Honeycomb встречает самолет на бесконечности (14.08.2014)
- Дэнни Калегари , Кляйниан, инструмент для визуализации кляйнианских групп, Геометрия и воображение, 4 марта 2014 г. [3]














