Алгоритм ОПТИКА

Упорядочение точек для определения структуры кластеризации ( ОПТИКА ) — это алгоритм поиска на основе плотности кластеры в пространственных данных. Его представили Михаэль Анкерст, Маркус М. Бройниг, Ханс-Петер Кригель и Йорг Зандер. Его основная идея аналогична DBSCAN . но он устраняет один из основных недостатков DBSCAN: проблему обнаружения значимых кластеров в данных различной плотности. Для этого точки базы данных (линейно) упорядочиваются так, что пространственно ближайшие точки становятся соседями в порядке. Кроме того, для каждой точки сохраняется специальное расстояние, представляющее плотность, которую необходимо принять для кластера, чтобы обе точки принадлежали одному кластеру. Это представлено в виде дендрограммы .

Основная идея

Как и DBSCAN , OPTICS требует два параметра: ε , который описывает максимальное расстояние (радиус), которое необходимо учитывать, и MinPts , описывающий количество точек, необходимых для формирования кластера. Точка p является базовой точкой как минимум точки MinPts. найдено , если в ее ε -окрестности $N_{\varepsilon }(p)$ (включая саму точку p ). В отличие от DBSCAN , OPTICS также учитывает точки, которые являются частью более плотно упакованного кластера, поэтому каждой точке назначается основное расстояние , которое описывает расстояние до MinPts ближайшей точки :

${\text{core-dist}}_{\mathit {\varepsilon ,MinPts}}(p)={\begin{cases}{\text{UNDEFINED}}&{\text{if }}|N_{\varepsilon }(p)|<{\mathit {MinPts}}\\{\mathit {MinPts}}{\text{-th smallest distance in }}N_{\varepsilon }(p)&{\text{otherwise}}\end{cases}}$

Расстояние достижимости другой точки o от точки p — это либо расстояние между o и p , либо основное расстояние p , в зависимости от того, что больше:

${\text{reachability-dist}}_{\mathit {\varepsilon ,MinPts}}(o,p)={\begin{cases}{\text{UNDEFINED}}&{\text{if }}|N_{\varepsilon }(p)|<{\mathit {MinPts}}\\\max({\text{core-dist}}_{\mathit {\varepsilon ,MinPts}}(p),{\text{dist}}(p,o))&{\text{otherwise}}\end{cases}}$

Если p и o — ближайшие соседи, это $\varepsilon '<\varepsilon$ нам нужно предположить, что p и o принадлежат одному и тому же кластеру.

И расстояние ядра, и расстояние достижимости не определены, если достаточно плотный кластер (по отношению к ε отсутствует ). При достаточно большом ε этого никогда не происходит, но тогда каждый запрос ε -соседства возвращает всю базу данных, что приводит к $O(n^{2})$ время выполнения. Следовательно, параметр ε необходим для отсекания плотности кластеров, которые больше не интересны, и для ускорения алгоритма.

Параметр ε , строго говоря, не обязателен. Его можно просто установить на максимально возможное значение. Однако когда пространственный индекс доступен, он играет практическую роль в отношении сложности. OPTICS абстрагируется от DBSCAN, удаляя этот параметр, по крайней мере, до такой степени, что ему приходится указывать только максимальное значение.

Псевдокод

Базовый подход OPTICS аналогичен DBSCAN , но вместо сохранения известных, но пока необработанных элементов кластера в наборе, они сохраняются в приоритетной очереди (например, с использованием индексированной кучи ).

function OPTICS(DB, ε, MinPts) is
    for each point p of DB do
        p.reachability-distance = UNDEFINED
    for each unprocessed point p of DB do
        N = getNeighbors(p, ε)
        mark p as processed
        output p to the ordered list
        if core-distance(p, ε, MinPts) != UNDEFINED then
            Seeds = empty priority queue
            update(N, p, Seeds, ε, MinPts)
            for each next q in Seeds do
                N' = getNeighbors(q, ε)
                mark q as processed
                output q to the ordered list
                if core-distance(q, ε, MinPts) != UNDEFINED do
                    update(N', q, Seeds, ε, MinPts)

В update() приоритетная очередь Seeds обновляется с помощью $\varepsilon$- окрестности $p$ и $q$, соответственно:

function update(N, p, Seeds, ε, MinPts) is
    coredist = core-distance(p, ε, MinPts)
    for each o in N
        if o is not processed then
            new-reach-dist = max(coredist, dist(p,o))
            if o.reachability-distance == UNDEFINED then // o is not in Seeds
                o.reachability-distance = new-reach-dist
                Seeds.insert(o, new-reach-dist)
            else               // o in Seeds, check for improvement
                if new-reach-dist < o.reachability-distance then
                    o.reachability-distance = new-reach-dist
                    Seeds.move-up(o, new-reach-dist)

Таким образом, ОПТИКА выводит точки в определенном порядке, аннотируя их наименьшее расстояние достижимости (в исходном алгоритме также экспортируется основное расстояние, но это не требуется для дальнейшей обработки).

Извлечение кластеров

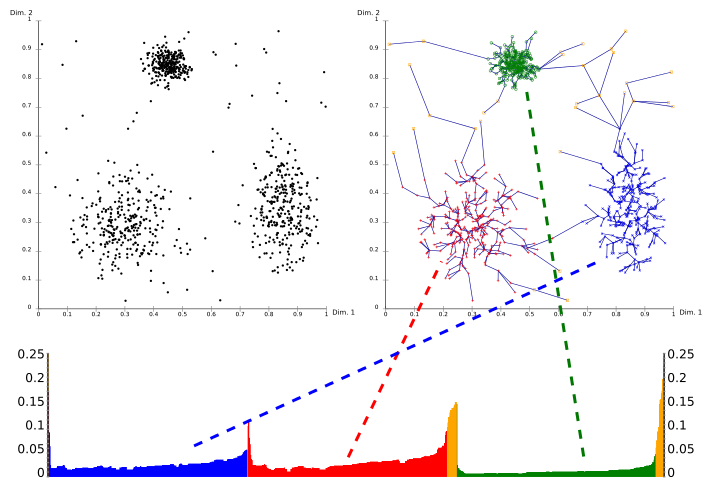
Используя график достижимости (особый вид дендрограммы ), можно легко получить иерархическую структуру кластеров. Это двумерный график с упорядочением точек, обработанных ОПТИКОЙ, по оси X и расстоянием достижимости по оси Y. Поскольку точки, принадлежащие кластеру, имеют малое расстояние достижимости до ближайшего соседа, кластеры отображаются как впадины на графике достижимости. Чем глубже долина, тем плотнее скопление.

Изображение выше иллюстрирует эту концепцию. В верхней левой области показан синтетический пример набора данных. Верхняя правая часть визуализирует связующее дерево, созданное OPTICS, а нижняя часть показывает график достижимости, рассчитанный OPTICS. Цвета на этом графике являются метками и не вычисляются алгоритмом; но хорошо видно, как впадины на графике соответствуют кластерам в приведенном выше наборе данных. Желтые точки на этом изображении считаются шумом, и на их графике достижимости не обнаружено впадин. Обычно они не назначаются кластерам, за исключением вездесущего кластера «все данные» в иерархическом результате.

Извлечение кластеров из этого графика можно выполнить вручную, выбрав диапазоны по оси X после визуального осмотра, выбрав пороговое значение по оси Y (результат будет аналогичен результату кластеризации DBSCAN с тем же $\varepsilon$ и параметры minPts; здесь значение 0,1 может дать хорошие результаты) или с помощью различных алгоритмов, которые пытаются обнаружить впадины по крутизне, обнаружению перегиба или локальным максимумам. Участок участка, начинающийся с крутого спуска и заканчивающийся крутым подъемом, считается долиной и соответствует прилегающей территории с высокой плотностью застройки. Необходимо уделить дополнительное внимание последним точкам впадины, чтобы отнести их к внутреннему или внешнему кластеру. Этого можно добиться, рассматривая предшественника. Кластеризации, полученные таким способом, обычно являются иерархическими и не могут быть достигнуты за один запуск DBSCAN.

Сложность

Как и DBSCAN , OPTICS обрабатывает каждую точку один раз и выполняет один $\varepsilon$-запрос соседства во время этой обработки. Учитывая пространственный индекс , который предоставляет запрос о соседстве в $O(\log n)$ время выполнения, общее время выполнения $O(n\cdot \log n)$ получается. Однако худший случай $O(n^{2})$, как и в случае с DBSCAN. Авторы оригинальной статьи OPTICS сообщают о фактическом постоянном коэффициенте замедления 1,6 по сравнению с DBSCAN. Обратите внимание, что значение $\varepsilon$ может сильно повлиять на стоимость алгоритма, поскольку слишком большое значение может повысить стоимость запроса окрестности до линейной сложности.

В частности, выбирая $\varepsilon >\max _{x,y}d(x,y)$ (больше максимального расстояния в наборе данных) возможно, но приводит к квадратичной сложности, поскольку каждый запрос окрестности возвращает полный набор данных. Даже если пространственный индекс недоступен, это требует дополнительных затрат на управление кучей. Поэтому, $\varepsilon$ следует выбирать соответствующим образом для набора данных.

Расширения

ОПТИКА-О — это алгоритм обнаружения выбросов, основанный на ОПТИКЕ. Основное использование — это извлечение выбросов из существующей серии ОПТИКИ с меньшими затратами по сравнению с использованием другого метода обнаружения выбросов. Более известная версия LOF основана на тех же концепциях.

ДеЛи-Клю, Density-Link-Clustering сочетает в себе идеи односвязной кластеризации и ОПТИКИ, устраняя $\varepsilon$ параметр и предлагает улучшение производительности по сравнению с ОПТИКОЙ.

HiSC - это метод иерархической подпространственной кластеризации (параллельно осям), основанный на ОПТИКЕ.

HICO — это алгоритм иерархической корреляционной кластеризации , основанный на ОПТИКЕ.

Блюдо является улучшением по сравнению с HiSC, позволяющим находить более сложные иерархии.

ФОПТИКА это более быстрая реализация с использованием случайных проекций.

HDBSCAN* основан на усовершенствовании DBSCAN, исключающем граничные точки из кластеров и, таким образом, более строго следуя базовому определению уровней плотности Хартигана.

Доступность

Java-реализации OPTICS, OPTICS-OF, DeLi-Clu, HiSC, HiCO и DiSH доступны в среде интеллектуального анализа данных ELKI (с индексным ускорением для нескольких функций расстояния и с автоматическим извлечением кластеров с использованием метода извлечения ξ). Другие реализации Java включают расширение Weka (без поддержки извлечения ξ-кластера).

Пакет R «dbscan» включает реализацию OPTICS на C++ (как с традиционным dbscan, так и с извлечением кластеров ξ), использующую дерево kd для ускорения индекса только для евклидова расстояния.

Реализации OPTICS на Python доступны в библиотеке PyClustering и в scikit-learn . HDBSCAN* доступен в библиотеке hdbscan .