Генерация второй гармоники

Не путать с двухфотонным поглощением .

Схема энергетических уровней процесса ГВГ

Генерация второй гармоники ( ГВГ ), также известная как удвоение частоты , представляет собой волново-волновое нелинейное взаимодействие низшего порядка, которое происходит в различных системах, включая оптические, радио, атмосферные и магнитогидродинамические системы. В качестве прототипа поведения волн ГВГ широко используется, например, при удвоении частоты лазеров. Первоначально ГВГ был обнаружен как нелинейный оптический процесс. в котором два фотона с одинаковой частотой взаимодействуют с нелинейным материалом, «объединяются» и генерируют новый фотон с удвоенной энергией исходных фотонов (эквивалентно удвоенной частоте и половине волны ), что сохраняет когерентность длины возбуждение. Это частный случай генерации суммарной частоты (2 фотона) и, в более общем смысле, генерации гармоник .

второго порядка Нелинейная восприимчивость среды характеризует ее склонность вызывать ГВГ. Генерация второй гармоники, как и другие нелинейно-оптические явления четного порядка, не допускается в средах с инверсионной симметрией (по ведущему электродипольному вкладу). Однако такие эффекты, как сдвиг Блоха – Зигерта (колебания), обнаруженный, когда двухуровневые системы возбуждаются на частотах Раби, сравнимых с их частотами перехода, приводят к генерации второй гармоники в центросимметричных системах. Кроме того, в нецентросимметричных кристаллах, относящихся к кристаллографической точечной группе 432, ГВГ невозможна. и по условиям Клейнмана ГВГ в 422 и 622 точечных группах должна исчезнуть, хотя существуют некоторые исключения.

В некоторых случаях почти 100% световой энергии можно преобразовать в частоту второй гармоники. Эти случаи обычно включают в себя интенсивные импульсные лазерные лучи, проходящие через большие кристаллы и тщательное выравнивание для получения фазового синхронизма . В других случаях, например, в микроскопии изображений второй гармоники , лишь небольшая часть энергии света преобразуется во вторую гармонику, но этот свет, тем не менее, можно обнаружить с помощью оптических фильтров .

Генерация второй гармоники, часто называемая удвоением частоты, также является процессом в радиосвязи; он был разработан в начале 20 века и использовался на частотах мегагерцового диапазона. Это частный случай умножения частоты .

История

Электрон (фиолетовый) толкается из стороны в сторону под действием синусоидально колеблющейся силы, то есть электрического поля света. Но поскольку электрон находится в ангармонической среде потенциальной энергии (черная кривая), движение электрона не является синусоидальным. Три стрелки показывают ряд Фурье движения: синяя стрелка соответствует обычной (линейной) восприимчивости , зеленая стрелка соответствует генерации второй гармоники, а красная стрелка соответствует оптическому выпрямлению .

Генерация второй гармоники была впервые продемонстрирована Питером Франкеном , А. Э. Хиллом, К. В. Питерсом и Г. Вайнрайхом в Мичиганском университете , Анн-Арбор, в 1961 году. Демонстрация стала возможной благодаря изобретению лазера , который создавал необходимый когерентный свет высокой интенсивности. Они сфокусировали рубиновый лазер с длиной волны 694 нм на образец кварца. Они направили выходной свет через спектрометр , записав спектр на фотобумагу, что указывало на образование света с длиной волны 347 нм. Известно, что при публикации в журнале Physical Review Letters редактор принял тусклое пятно (347 нм) на фотобумаге за пятнышко грязи и удалил его из публикации. Формула ГСП была первоначально описана Н. Блюмбергеном и П.С. Першаном в Гарварде в 1962 году. В их обширной оценке уравнений Максвелла на плоской границе раздела линейной и нелинейной среды были разъяснены несколько правил взаимодействия света в нелинейных средах.

Типы в кристаллах

Критическое фазовое согласование

Различные типы фазового согласования генерации второй гармоники когерентного света для сильного преобразования. Случай отрицательных кристаллов ( $n_{o}>n_{e}$), инвертируйте индексы, если положительный кристалл ( $n_{e}>n_{o}$).

Генерация второй гармоники происходит трех типов для критического синхронизма: обозначаются 0, I и II. В ГВГ типа 0 два фотона, имеющие необычную поляризацию по отношению к кристаллу, объединятся, чтобы сформировать одиночный фотон с удвоенной частотой/энергией и необычной поляризацией. В ГВГ типа I два фотона, имеющие обычную поляризацию по отношению к кристаллу, объединятся, чтобы сформировать один фотон с удвоенной частотой и необыкновенной поляризацией. В ГВГ типа II два фотона, имеющие ортогональную поляризацию, объединятся, чтобы сформировать один фотон с удвоенной частотой и обычной поляризацией. Для данной ориентации кристалла происходит только один из этих типов ГВГ. В общем, для использования типа 0 взаимодействий с квазисинхронизмом потребуется тип кристалла , например, ниобат лития с периодической поляризацией (PPLN).

Некритическое синхронизм

Поскольку процесс фазового синхронизма по сути означает адаптацию оптических показателей n при ω и 2ω, в некоторых кристаллах с двойным лучепреломлением его также можно осуществить путем регулирования температуры, поскольку n меняется с температурой. Например, LBO демонстрирует идеальный синхронизм при 25 °C для ГВГ, возбужденного на длине волны 1200 или 1400 нм. но для ГВГ с обычной лазерной линией 1064 нм ее необходимо повысить до 200 °C. Он называется «некритичным», поскольку не зависит от ориентации кристалла, как обычный синхронизм.

Оптическая генерация второй гармоники

Схема процесса генерации второй гармоники

Поскольку средам с инверсионной симметрией запрещено генерировать свет второй гармоники за счет вклада электрического диполя ведущего порядка (в отличие от генерации третьей гармоники ), поверхности и интерфейсы представляют собой интересные объекты для изучения с помощью ГВГ. Фактически, генерация второй гармоники и генерация суммарной частоты дискриминируют сигналы из объема, неявно маркируя их как методы, специфичные для поверхности. В 1982 году Т.Ф. Хайнц и Ю.Р. Шен впервые явно продемонстрировали, что ГВГ можно использовать в качестве спектроскопического метода для исследования молекулярных монослоев, адсорбированных на поверхности. Хайнц и Шен адсорбировали монослои лазерного красителя родамина на плоскую поверхность плавленого кварца ; затем поверхность с покрытием накачивалась наносекундным сверхбыстрым лазером. Свет ВГ с характерными спектрами адсорбированной молекулы и ее электронных переходов измерялся при отражении от поверхности и демонстрировал квадратичную зависимость мощности от мощности лазера накачки.

В спектроскопии ГВГ основное внимание уделяется измерению двойной частоты падающего сигнала 2 ω при наличии падающего электрического поля. $E(\omega )$ для раскрытия информации о поверхности. Проще говоря (более подробный вывод см. ниже), индуцированный диполь второй гармоники на единицу объема: $P^{(2)}(2\omega )$, можно записать как

$E(2\omega )\propto P^{(2)}(2\omega )=\chi ^{(2)}E(\omega )E(\omega )$

где $\chi ^{(2)}$ известен как тензор нелинейной восприимчивости и является характеристикой материалов на границе раздела исследования. Сгенерированный $E(2\omega )$ и соответствующие $\chi ^{(2)}$ Было показано, что они раскрывают информацию об ориентации молекул на поверхности/границе раздела, межфазной аналитической химии поверхностей и химических реакциях на границах раздела.

С плоских поверхностей

Основная статья: Генерация поверхностной второй гармоники

Изображение установки генерации второй гармоники для измерения ориентации фенола на границе раздела воздух-вода.

Ранние эксперименты в этой области продемонстрировали генерацию второй гармоники на металлических поверхностях. В конце концов, ГВГ был использован для исследования границы раздела воздух-вода, что позволило получить подробную информацию об ориентации и упорядочении молекул на одной из самых распространенных поверхностей. Можно показать, что отдельные элементы $\chi ^{(2)}$:

${\begin{aligned}\chi _{zzz}^{(2)}&=N_{s}\left\langle \cos ^{3}(\theta )\right\rangle \alpha _{zzz}^{(2)}\\\chi _{xzx}^{(2)}&={\frac {1}{2}}N_{s}\left\langle \cos(\theta )\sin ^{2}(\theta )\right\rangle \alpha _{zzz}^{(2)}\end{aligned}}$

где N _s — плотность адсорбата, θ — угол, который ось z молекулы составляет с нормалью к поверхности Z , и $\alpha _{zzz}^{(2)}$ является доминирующим элементом нелинейной поляризуемости молекулы на границе раздела, позволяет определить θ по заданным лабораторным координатам ( x , y , z ) . Используя метод интерференционной ГВГ для определения этих элементов χ (2), первое измерение молекулярной ориентации показало, что гидроксильная группа фенола направлена ​​вниз, в воду на границе раздела воздух-вода (как и ожидалось, из-за способности гидроксильных групп образовывать водородные связи). Кроме того, ГВГ на плоских поверхностях выявила различия в pK. ^а и вращательные движения молекул на границах раздела.

С неплоских поверхностей

Мультфильм, изображающий упорядоченные молекулы на небольшой сферической поверхности. Сверхбыстрый лазер накачки излучает свет с частотой ω, который генерирует свет с частотой 2ω из локально нецентросимметричной среды.

Свет второй гармоники также может генерироваться от поверхностей, которые являются «локально» плоскими, но могут иметь инверсионную симметрию (центросимметричную) в более крупном масштабе. В частности, недавняя теория продемонстрировала, что ГВГ от небольших сферических частиц (микро- и нанометрового масштаба) возможна при правильном учете рэлеевского рассеяния (рассеяние без изменения частоты от поглощенных волн к излучаемым). На поверхности небольшой сферы инверсионная симметрия нарушается, что позволяет возникать ГВГ и другим гармоникам четного порядка.

Для коллоидной системы микрочастиц при относительно низких концентрациях общий сигнал SH $I_{2\omega }^{\text{total}}$, определяется:

$I_{2\omega }^{\text{total}}\propto \sum \limits _{j=1}^{n}\left(E_{j}^{2\omega }\right)^{2}=n\left(E^{2\omega }\right)^{2}=nI_{2\omega }$

где $E_{j}^{2\omega }$ – электрическое поле ВГ, создаваемое j -й частицей, n – плотность частиц. Свет SH, генерируемый каждой частицей, является когерентным , но некогерентно складывается со светом SH, генерируемым другими частицами (пока плотность достаточно низка). Таким образом, свет ВГ генерируется только на границах разделов сфер и их окружения и не зависит от межчастичных взаимодействий. Было также показано, что электрическое поле второй гармоники $E(2\omega )$ масштабируется с кубом радиуса частицы, a ³ .

Помимо сфер, ГВГ аналогичным образом изучала и другие мелкие частицы, такие как стержни. Могут быть исследованы как иммобилизованные, так и коллоидные системы малых частиц. Недавние эксперименты с использованием генерации второй гармоники непланарных систем включают кинетику транспорта через мембраны живых клеток. и демонстрация ГВГ в сложных наноматериалах .

Диаграмма направленности

Диаграмма излучения ГВГ, возбуждаемая гауссовским пучком, в однородной среде (А) или на границе раздела противоположных полярностей, параллельной распространению (Б). Представлена ​​только передняя ГСП.

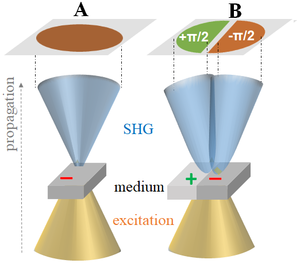
Диаграмма излучения ГВГ, генерируемая возбуждающим гауссовским пучком, также имеет (однородный) двумерный гауссов профиль, если возбуждаемая нелинейная среда однородна (А). Однако, если возбуждающий луч расположен на границе раздела противоположных полярностей (± граница, B ), параллельной распространению луча (см. рисунок), ГВГ будет разделена на два лепестка, амплитуды которых имеют противоположный знак, т.е. $\pi$ сдвинутый по фазе.

Эти границы можно найти саркомерах мышц в (белок = миозин , например, ). Обратите внимание, что мы рассмотрели здесь только прямое поколение.

См. Также: Микроскопия визуализации второй гармоники § Прямое и обратное ГВГ.

ГВГ Более того, синхронизм также может привести к ${\vec {k}}_{2\omega }=-2{\vec {k}}_{\omega }$: некоторое количество ГВГ также излучается в обратном направлении (эпи-направление). Когда фазовый синхронизм не выполняется, как в биологических тканях , обратный сигнал возникает из-за достаточно высокого фазового рассогласования, что позволяет компенсировать его небольшим обратным вкладом. В отличие от флуоресценции, пространственная когерентность процесса ограничивает его излучение только в этих двух направлениях, но длина когерентности в обратном направлении всегда намного меньше, чем в прямом, а это означает, что прямого сигнала ГВГ всегда больше, чем обратного.

Диаграмма направленности ГВГ в прямом (F) и обратном (B) направлении от различного расположения диполей: (a) одиночные диполи, таким образом, F = B ; (б) небольшая стопка диполей F > B ; (в) большая стопка диполей F >> B ; (d) фазовый сдвиг Гуи отменяет ГВГ, F и B слабые

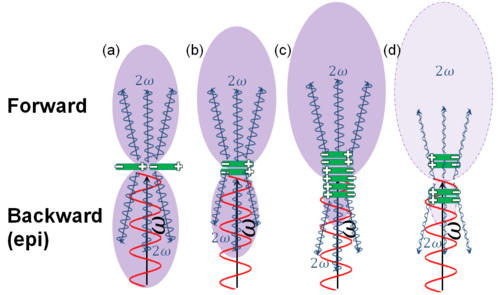
Соотношение прямого ( F ) и обратного ( B ) зависит от расположения различных диполей (зеленых на рисунке), которые возбуждаются. При наличии только одного диполя ((a) на рисунке) F = B , но F становится выше, чем B , когда больше диполей укладываются вдоль направления распространения (b и c). Однако фазовый сдвиг Гуи гауссова луча будет означать $\pi$ фазовый сдвиг между ГВГ, генерируемыми на краях фокального объема, и, таким образом, может привести к деструктивным интерференциям (нулевой сигнал), если на этих краях имеются диполи, имеющие одинаковую ориентацию (случай (d) на рисунке).

Приложения

Зеленые лазеры

Генерация второй гармоники используется в лазерной промышленности для изготовления зеленых лазеров с длиной волны 532 нм из источника с длиной волны 1064 нм. Свет с длиной волны 1064 нм проходит через объемный нелинейный кристалл (обычно изготовленный из KDP или KTP ). В высококачественных диодных лазерах кристалл на выходе покрыт инфракрасным фильтром, чтобы предотвратить утечку интенсивного инфракрасного света с длиной волны 1064 нм или 808 нм в луч. Обе эти длины волн невидимы и не вызывают в глазу защитной реакции «мигания-рефлекса» и поэтому могут представлять особую опасность для глаз человека. Кроме того, некоторые защитные очки, предназначенные для аргоновых или других зеленых лазеров, могут отфильтровывать зеленый компонент (давая ложное ощущение безопасности), но передавать инфракрасное излучение. некоторые продукты с «зелеными лазерными указками », в которых отсутствует дорогой инфракрасный фильтр, часто без предупреждения. Тем не менее, на рынке появились

Измерение сверхкоротких импульсов

Генерация второй гармоники также используется для измерения ширины ультракоротких импульсов с помощью автокорреляторов . Охарактеризовать ультракороткий импульс (например, измерить его временную ширину) невозможно непосредственно с помощью электроники, поскольку временной масштаб составляет менее 1 пс ( $10^{-12}$сек): необходимо использовать сам импульс, поэтому часто используется автокорреляционная функция. Преимущество ГВГ заключается в смешивании двух входных полей для генерации гармонического поля, поэтому он является хорошим кандидатом (но не единственным) для выполнения такого измерения импульсов. Оптическая автокорреляция , в ее версии по интенсивности или с разрешением по краям ( интерферометрической ), использует ГВГ, в отличие от автокорреляции полей . Кроме того, большинство версий FROG ( называемых SHG-FROG) используют SHG для смешивания задержанных полей.

Микроскопия генерации второй гармоники

Основная статья: Микроскопия визуализации второй гармоники

В биологической и медицинской науке эффект генерации второй гармоники используется для оптической микроскопии высокого разрешения. Из-за ненулевого коэффициента второй гармоники только нецентросимметричные структуры способны излучать свет ГВГ. Одной из таких структур является коллаген, который содержится в большинстве несущих нагрузку тканей. Используя короткоимпульсный лазер, такой как фемтосекундный лазер , и набор соответствующих фильтров, возбуждающий свет можно легко отделить от излучаемого сигнала ГВГ с удвоенной частотой. Это обеспечивает очень высокое осевое и латеральное разрешение, сравнимое с разрешением конфокальной микроскопии, без использования точечных отверстий. ГВГ-микроскопия использовалась для исследования роговицы . и пластинчатая склера оба из которых состоят в основном из коллагена. Генерацию второй гармоники можно производить с помощью нескольких нецентросимметричных органических красителей; однако большинство органических красителей также генерируют побочную флуоресценцию наряду с сигналами генерации второй гармоники. До сих пор было показано только два класса органических красителей, которые не производят побочной флуоресценции и работают исключительно за счет генерации второй гармоники. Недавно, используя флуоресценцию с двухфотонным возбуждением и микроскопию на основе генерации второй гармоники, группа исследователей Оксфордского университета показала, что молекулы органического типа порфирина могут иметь разные дипольные моменты перехода для двухфотонной флуоресценции и генерации второй гармоники. которые в противном случае считаются возникающими из-за одного и того же дипольного момента перехода.

Микроскопия генерации второй гармоники также используется в материаловедении, например, для характеристики наноструктурированных материалов.

Характеристика кристаллических материалов

Генерация второй гармоники также важна для характеристики органических или неорганических кристаллов. поскольку это один из наиболее дискриминантных и быстрых методов обнаружения нецентросимметрии . Кроме того, этот метод можно использовать как для монокристаллов, так и для порошкообразных образцов. Следует напомнить, что ГВГ возможна (из объема) только в нецентросимметричных (НК) кристаллах . Доля нецентросимметричных кристаллов в природе значительно ниже центросимметричных кристаллов (около 22% Кембриджской структурной базы данных). ), но частота кристаллов NC значительно увеличивается в фармацевтической, биологической и электронной областях из-за особых свойств этих кристаллов ( пьезоэлектричество , пироэлектричество , полярные фазы, хиральность и т. д.).

В 1968 году (через 7 лет после первого экспериментального подтверждения ГВГ на монокристалле ), Курц и Перри начали разработку анализатора ГВГ для быстрого обнаружения наличия или отсутствия центра инверсии в порошкообразных кристаллических образцах. Было показано, что обнаружение сигнала ГВГ является надежным и чувствительным тестом для обнаружения кристаллической нецентросимметрии с уровнем достоверности более 99%. Это подходящий инструмент для разрешения неоднозначностей пространственной группы, которые могут возникнуть из-за закона Фриделя в монокристаллической дифракции рентгеновских лучей. Кроме того, этот метод упоминается в Международных таблицах кристаллографии и описывается как «мощный метод проверки кристаллических материалов на отсутствие центра симметрии».

Одним из возможных применений также является быстрое распознавание хиральных фаз, таких как конгломерат , которые представляют особый интерес для фармацевтической промышленности. Его также можно использовать в качестве метода проверки структурной чистоты материала, если одна из примесей представляет собой NC, достигая порога обнаружения всего 1 ppm. с использованием аппарата Курца-Перри до одной части на 10 миллиардов по объему с использованием микроскопа ГВГ.

Благодаря высокой чувствительности метода он может быть полезным инструментом для точного определения фазовой диаграммы. а также может использоваться для контроля фазовых переходов ( полиморфный переход, дегидратация,...), когда хотя бы одна из фаз является NC.

Теоретический вывод (плоская волна)

При низкой конверсии

Простейшим случаем для анализа генерации второй гармоники является плоская волна амплитуды E ( ω ), бегущая в нелинейной среде в направлении ее k вектора . Поляризация генерируется на частоте второй гармоники:

$P(2\omega )=\varepsilon _{0}\chi ^{(2)}E^{2}(\omega )=2\varepsilon _{0}d_{\text{eff}}(2\omega ;\omega ,\omega )E^{2}(\omega ),\,$

где $d_{\text{eff}}$ – эффективный нелинейно-оптический коэффициент, зависящий от конкретных компонентов $\chi ^{(2)}$ которые участвуют в этом конкретном взаимодействии. Волновое уравнение при 2ω (предполагая незначительные потери и утверждая приближение медленно меняющейся огибающей ) имеет вид

${\frac {\partial E(2\omega )}{\partial z}}=-{\frac {i\omega }{n_{2\omega }c}}d_{\text{eff}}E^{2}(\omega )e^{i\,\Delta k\,z}$

где $\Delta k=k(2\omega )-2k(\omega )$.

При низкой эффективности преобразования ( E (2 ω ) ≪ E ( ω )) амплитуда $E(\omega )$ остается практически постоянным по длине взаимодействия, $\ell$. Тогда с граничным условием $E(2\omega ,z=0)=0$ мы получаем

$E(2\omega ,z=\ell )=-{\frac {i\omega d_{\text{eff}}}{n_{2\omega }c}}E^{2}(\omega )\int _{0}^{\ell }e^{i\,\Delta k\,z}\,dz=-{\frac {i\omega d_{\text{eff}}}{n_{2\omega }c}}E^{2}(\omega )\ell \,{\frac {\sin \left({\frac {1}{2}}\,\Delta k\,\ell \right)}{{\frac {1}{2}}\,\Delta k\,\ell }}e^{{\frac {i}{2}}\,\Delta k\,\ell }$

Что касается оптической интенсивности, $I=n/2{\sqrt {\varepsilon _{0}/\mu _{0}}}|E|^{2}$, Это,

$I(2\omega ,\ell )={\frac {2\omega ^{2}d_{\text{eff}}^{2}\ell ^{2}}{n_{2\omega }n_{\omega }^{2}c^{3}\varepsilon _{0}}}\left({\frac {\sin \left({\frac {1}{2}}\,\Delta k\,\ell \right)}{{\frac {1}{2}}\,\Delta k\,\ell }}\right)^{2}I^{2}(\omega )$

Эта интенсивность максимальна для условия фазового синхронизма Δ k = 0. Если процесс не синхронизирован, движущая поляризация в точке ω входит и противофазирует с генерируемой волной E (2 ω ), и преобразование колеблется как sin(Δ kℓ /2). Длина когерентности определяется как $\ell _{c}={\frac {\pi }{\Delta k}}$. Нецелесообразно использовать нелинейный кристалл, длина которого намного превышает длину когерентности. ( Периодическая поляризация и квазисинхронизм предлагают другой подход к этой проблеме.)

С истощением

Схема генерации второй гармоники с идеальным фазовым синхронизмом $\Delta k=0$.

Схема генерации второй гармоники с несовершенным фазовым синхронизмом $\Delta k\neq 0$. В этом случае энергия течет вперед и назад от накачки к сигналу с удвоенной частотой, а наличие толстого кристалла может привести к меньшему количеству производимого ГВГ.

Когда преобразование во 2-ю гармонику становится существенным, становится необходимым включить обеднение основной гармоники. Преобразование энергии утверждает, что все задействованные поля подтверждают соотношения Мэнли-Роу . Тогда имеем связанные уравнения:

${\begin{aligned}{\frac {\partial E(2\omega )}{\partial z}}&=-{\frac {i\omega }{n_{2\omega }c}}d_{\text{eff}}E^{2}(\omega )e^{i\,\Delta k\,z},\\[5pt]{\frac {\partial E(\omega )}{\partial z}}&=-{\frac {i\omega }{n_{\omega }c}}d_{\text{eff}}^{*}E(2\omega )E^{*}(\omega )e^{-i\,\Delta k\,z},\end{aligned}}$

где $*$ обозначает комплексно-сопряженное. Для простоты предположим, что синхронная генерация ( $\Delta k=0$). Тогда энергосбережение требует, чтобы

$n_{2\omega }\left[E^{*}(2\omega ){\frac {\partial E(2\omega )}{\partial z}}+{\text{c.c.}}\right]=-n_{\omega }\left[E(\omega ){\frac {\partial E^{*}(\omega )}{\partial z}}+{\text{c.c.}}\right]$

где ${\text{c.c.}}$ является комплексно-сопряженным другим термином, или

$n_{2\omega }\left|E(2\omega )\right|^{2}+n_{\omega }|E(\omega )|^{2}=n_{2\omega }E_{0}^{2}.$

Фазосинхронная ГВГ с истощением источника (синий) и соответствующим возбуждением (оранжевый). L — длина взаимодействия ( ℓ в тексте).

Теперь решим уравнения с посылкой

${\begin{aligned}E(\omega )&=\left|E(\omega )\right|e^{i\varphi (\omega )}\\E(2\omega )&=\left|E(2\omega )\right|e^{i\varphi (2\omega )}\end{aligned}}$

и получить

${\frac {d\left|E(2\omega )\right|}{dz}}=-{\frac {i\omega d_{\text{eff}}}{n_{\omega }c}}\left[E_{0}^{2}-\left|E(2\omega )\right|^{2}\right]e^{2i\varphi (\omega )-i\varphi (2\omega )}$

что приводит к

$\int _{0}^{\left|E(2\omega )\right|\ell }{\frac {d\left|E(2\omega )\right|}{E_{0}^{2}-\left|E(2\omega )\right|^{2}}}=-\int _{0}^{\ell }{\frac {i\omega d_{\text{eff}}}{n_{\omega }c}}e^{2i\varphi (\omega )-i\varphi (2\omega )}\,dz.$

С использованием

$\int {\frac {dx}{a^{2}-x^{2}}}={\frac {1}{a}}\tanh ^{-1}{\frac {x}{a}}$

мы получаем

$\left|E(2\omega )\right|_{z=\ell }=E_{0}\tanh \left({\frac {-iE_{0}\ell \omega d_{\text{eff}}}{n_{\omega }c}}e^{2i\varphi (\omega )-i\varphi (2\omega )}\right).$

Если мы предположим, что реальная $d_{\text{eff}}$, относительные фазы реального гармонического роста должны быть такими, что $e^{2i\varphi (\omega )-i\varphi (2\omega )}=i$. Затем

$I(2\omega ,\ell )=I(\omega ,0)\tanh ^{2}\left({\frac {E_{0}\omega d_{\text{eff}}\ell }{n_{\omega }c}}\right)$

или

$I(2\omega ,\ell )=I(\omega ,0)\tanh ^{2}(\Gamma \ell ),$

где $\Gamma =\omega d_{\text{eff}}E_{0}/nc$. От $I(2\omega ,\ell )+I(\omega ,\ell )=I(\omega ,0)$, отсюда также следует, что

$I(\omega ,\ell )=I(\omega ,0)\operatorname {sech} ^{2}(\Gamma \ell ).$

Теоретическое выражение с помощью гауссовских пучков

Предполагается, что волна возбуждения представляет собой гауссов пучок амплитуды: $A_{1}=A_{0}{\sqrt {\frac {2}{\pi }}}{\frac {z_{R}}{iq(z)}}\exp \left(ik_{1}{\frac {x^{2}+y^{2}}{2q(z)}}\right)$

с $q(z)=z-iz_{R}$, $z$ направление распространения, $z_{R}$ диапазон Рэлея, ${k}_{1}$ волновой вектор .

Каждая волна проверяет волновое уравнение

$\left[{\frac {\partial }{\partial x^{2}}}+{\frac {\partial }{\partial y^{2}}}+2ik_{1}{\frac {\partial }{\partial z}}\right]A(x,y,z;k_{1})={\begin{cases}0&{\text{for the fundamental}},\\{\frac {\omega _{n}^{2}c^{2}}{\chi ^{(n)}}}A(x,y,z;k_{1})e^{i\,\Delta k\,z}&{\text{for }}n{\text{-th harmonic}}.\end{cases}}$

где $\Delta k=k_{n}-k_{1}$.

С фазовым синхронизмом

Можно показать, что: $A_{n}=-i{\frac {\omega _{n}}{2n_{n\omega }c}}{\left(A_{0}{\sqrt {\frac {2}{\pi }}}\right)^{n}}z_{R}^{2}\int _{-\infty }^{z}{\frac {\chi ^{(n)}(u)}{q(u)^{2}}}\,du\exp \left(ik_{n}{\frac {x^{2}+y^{2}}{2q(z)}}\right)$

( гауссиан ), является решением уравнения ( n = 2 для ГВГ).

Нет фазового согласования

Интенсивность ГВГ, синхронизирована или нет. Предполагается, что ширина среды намного превышает z , диапазон Рэлея 20 мкм, длина волны возбуждения 0,8 мкм и оптический индекс 2,2.

Неидеальный синхронизм на практике является более реалистичным состоянием, особенно в биологических образцах. Однако предполагается, что параксиальное приближение все еще остается в силе: $k_{n}=nk_{1}$, а в гармоническом выражении $\chi ^{(n)}(z)$ сейчас $\chi ^{(n)}(z)e^{i\,\Delta k\,z}$.

В частном случае ГВГ ( n = 2) в среде длины L и положении фокуса $z_{0}$, интенсивность пишет:

$I_{2\omega }={\frac {2\omega ^{2}}{\pi c^{2}\varepsilon _{0}w_{0}^{2}n_{2\omega }n_{\omega }^{2}}}I_{\omega }^{2}(\chi ^{(2)})^{2}\left(\int _{z_{0}}^{z_{0}+L}{\frac {e^{i\,\Delta k\,z}}{1+iz/z_{R}}}\right)^{2}\,dz.$

где $c$ это скорость света в вакууме , $\varepsilon _{0}$ вакуума диэлектрическая проницаемость , $n_{n\omega }$ оптический показатель среды при $n\omega$ и $w_{0}$ возбуждения размер талии .

Таким образом, интенсивность ГВГ быстро затухает в объеме ( $0<z_{0}<L$), из-за фазового сдвига Гуи гауссова пучка.

В соответствии с экспериментами сигнал ГВГ исчезает в объеме (если толщина среды слишком велика), и ГВГ должна генерироваться на поверхности материала: поэтому преобразование не масштабируется строго с квадратом числа рассеивателей. , вопреки тому, что указывает модель плоских волн. Интересно, что сигнал также исчезает для более высоких порядков , таких как THG.

Используемые материалы

Материалами, способными генерировать вторую гармонику, являются кристаллы без инверсионной симметрии, за исключением кристаллов с точечной группой 432. При этом исключается вода и стекло.

Примечательно, что нитевидные биологические белки с цилиндрической симметрией, такие как коллаген , тубулин или миозин , а также некоторые углеводы (например, крахмал или целлюлоза ) также являются неплохими преобразователями ГВГ (основного в ближнем инфракрасном диапазоне).

Примеры кристаллов, используемых для преобразования ГВГ:

• Фундаментальное возбуждение при 600–1500 нм: БиБО (БиВ ₃ О ₆ )
• Фундаментальное возбуждение при 570–4000 нм: иодат лития LiIO ₃ .
• Фундаментальное возбуждение при 800–1100 нм, часто 860 или 980 нм: ниобат калия KNbO ₃ .
• Фундаментальное возбуждение при 410–2000 нм: BBO (β-BaB ₂ O ₄ ).
• Фундаментальное возбуждение при 984–3400 нм: КТР (КТиОПО ₄ ) или КТА.
• Фундаментальное возбуждение при ~1000–2000 нм: периодически поляризованные кристаллы типа PPLN .

Для распространенных типов твердотельных лазеров с диодной накачкой с входными длинами волн:

• 1064 нм: монофосфат калия KDP (KH ₂ PO ₄ ), триборат лития (LiB ₃ O ₅ ), CsLiB ₆ O ₁₀ и борат бария BBO(β-BaB ₂ O ₄ ).
• 1319 нм: KNbO ₃ , BBO (β-BaB ₂ O ₄ ), монокалийфосфат KDP (KH ₂ PO ₄ ), LiIO ₃ , LiNbO ₃ и титанилфосфат калия KTP (KTiOPO ₄ ).

См. также

• Генерация полугармоник
• Гармоническая генерация
• Нелинейная оптика
• Оптический умножитель частоты
• Микроскопия изображений второй гармоники
• Спонтанное параметрическое преобразование с понижением частоты
• Генерация поверхностной второй гармоники

Внешние ссылки

Статьи

• Парамесваран, КР; Курц-младший; Руссев, М.М.; Фейер (2002). «Наблюдение истощения накачки на 99% при однопроходной генерации второй гармоники в волноводе из ниобата лития с периодической поляризацией». Оптические письма . 27 (1): 43–45. Бибкод : 2002OptL...27...43P . дои : 10.1364/ол.27.000043 . ПМИД   18007710 .
• «Удвоение частоты» . Энциклопедия лазерной физики и техники . Проверено 4 ноября 2006 г.